LOGARITMO de um nmero real positivo O que

LOGARITMO de um número real positivo

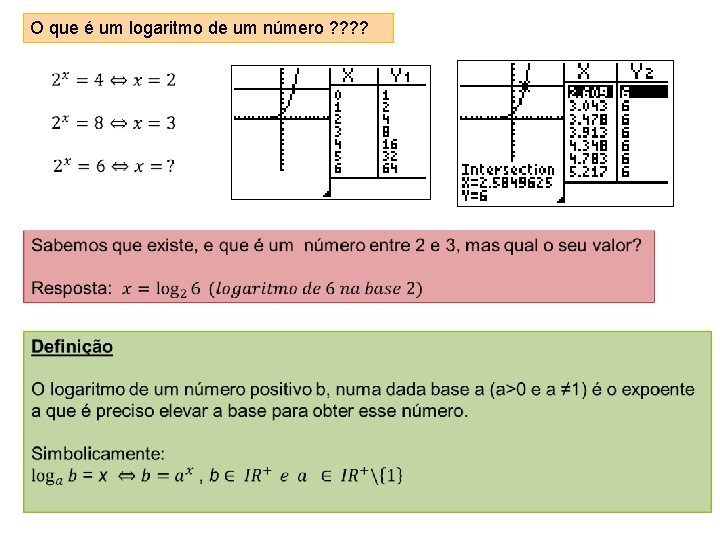
O que é um logaritmo de um número ? ?

Exercícios Manual, página 137, 14 ; página 138, 15 e página 139, 16 Os logaritmos também são úteis na resolução de equações exponenciais … Exercício, Manual, página 140, 17 e 18

UM POUCO DE HISTÓRIA …

Joost Bürgi um relojoeiro suíço a serviço do Duque de Hesse-Kassel, foi o primeiro a formar uma concepção sobre logaritmos. John Napier ( 1550 – 1617) ou John Nepper O método dos logaritmos de Napier contribuiu para o avanço da ciência, e especialmente a astronomia, fazendo com que cálculos muito difíceis se tornassem possíveis. Anterior à invenção de calculadoras e computadores, era uma ferramenta constantemente usada em observações, navegação e outros ramos da matemática prática. Além de sua imensa utilidade na realização de cálculos práticos, os logaritmos também têm um papel muito importante em matemática teórica.

Outros matemáticos, se envolveram com os logaritmos: Henry Briggs (1561 – 1630) Significado da palavra logaritmo William Oughtred (1575 – 1660) Johannes Keppler (1571 – 1630) LOGOS = razão ARITHOMOS = números

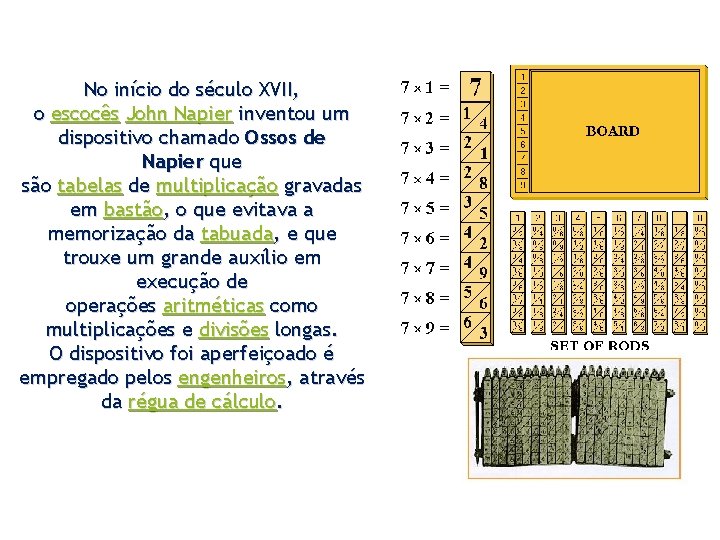
No início do século XVII, o escocês John Napier inventou um dispositivo chamado Ossos de Napier que são tabelas de multiplicação gravadas em bastão, o que evitava a memorização da tabuada, e que trouxe um grande auxílio em execução de operações aritméticas como multiplicações e divisões longas. O dispositivo foi aperfeiçoado é empregado pelos engenheiros, através da régua de cálculo.

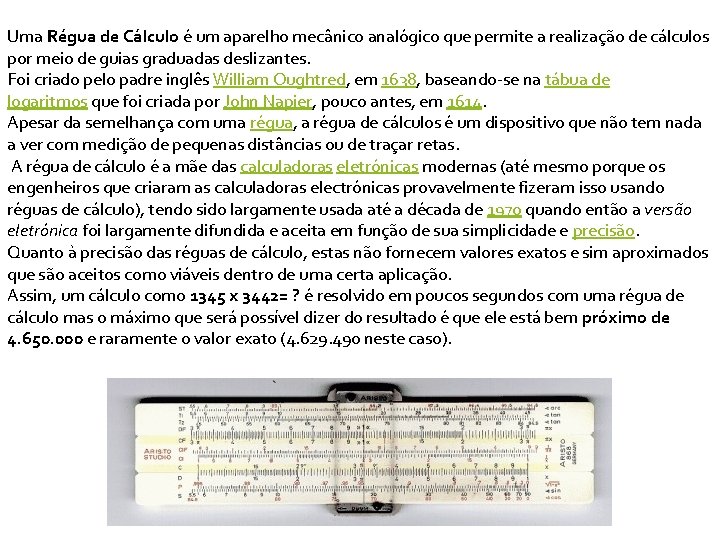
Uma Régua de Cálculo é um aparelho mecânico analógico que permite a realização de cálculos por meio de guias graduadas deslizantes. Foi criado pelo padre inglês William Oughtred, em 1638, baseando-se na tábua de logaritmos que foi criada por John Napier, pouco antes, em 1614. Apesar da semelhança com uma régua, a régua de cálculos é um dispositivo que não tem nada a ver com medição de pequenas distâncias ou de traçar retas. A régua de cálculo é a mãe das calculadoras eletrónicas modernas (até mesmo porque os engenheiros que criaram as calculadoras electrónicas provavelmente fizeram isso usando réguas de cálculo), tendo sido largamente usada até a década de 1970 quando então a versão eletrónica foi largamente difundida e aceita em função de sua simplicidade e precisão. Quanto à precisão das réguas de cálculo, estas não fornecem valores exatos e sim aproximados que são aceitos como viáveis dentro de uma certa aplicação. Assim, um cálculo como 1345 x 3442= ? é resolvido em poucos segundos com uma régua de cálculo mas o máximo que será possível dizer do resultado é que ele está bem próximo de 4. 650. 000 e raramente o valor exato (4. 629. 490 neste caso).

Como o matemático Pierre Laplace se referiu à descoberta e aplicação dos Logaritmos. «Ao diminuírem os cálculos, os logaritmos duplicaram a vida dos astrónomos …»

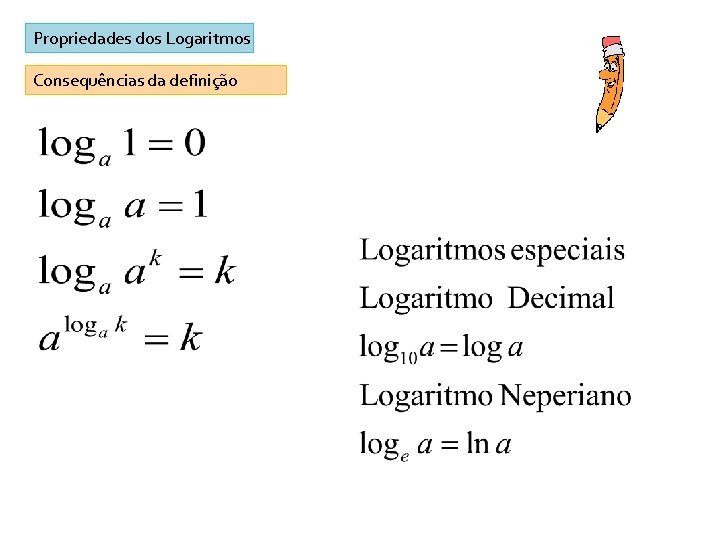
Propriedades dos Logaritmos Consequências da definição

Propriedades operatórias dos Logaritmos Mudança de base

Logaritmo do inverso Sendo x um número positivo: Propriedade: Exercícios Manual, página 145, 19, 20 e 21 Manual, página 159, 39 e 40

Definição de Função Logarítmica Chama-se Função Logarítmica a uma função do tipo : NOTA: A função logarítmica é a função inversa da função exponencial e vice-versa.

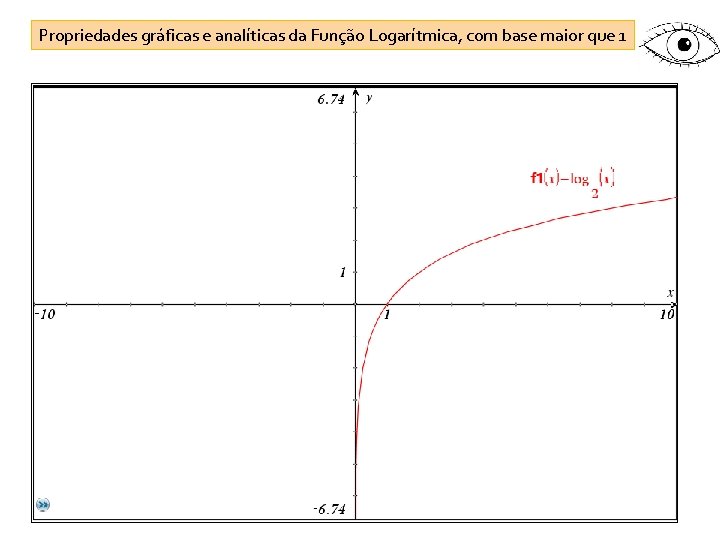
Propriedades gráficas e analíticas da Função Logarítmica, com base maior que 1

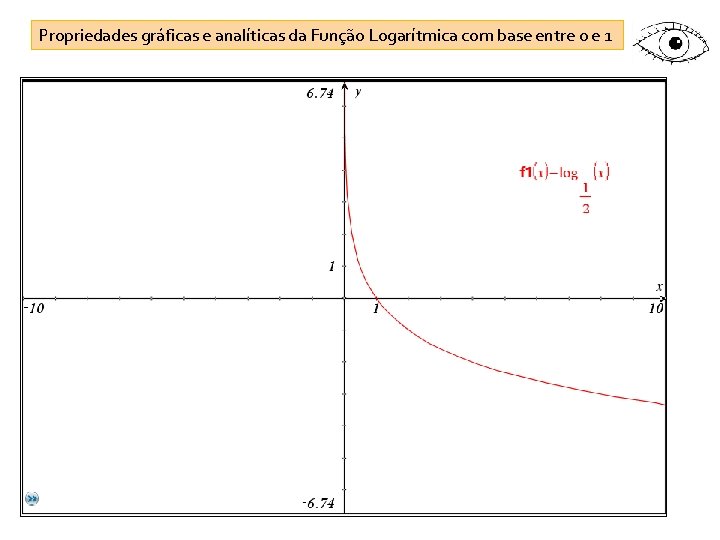
Propriedades gráficas e analíticas da Função Logarítmica com base entre 0 e 1

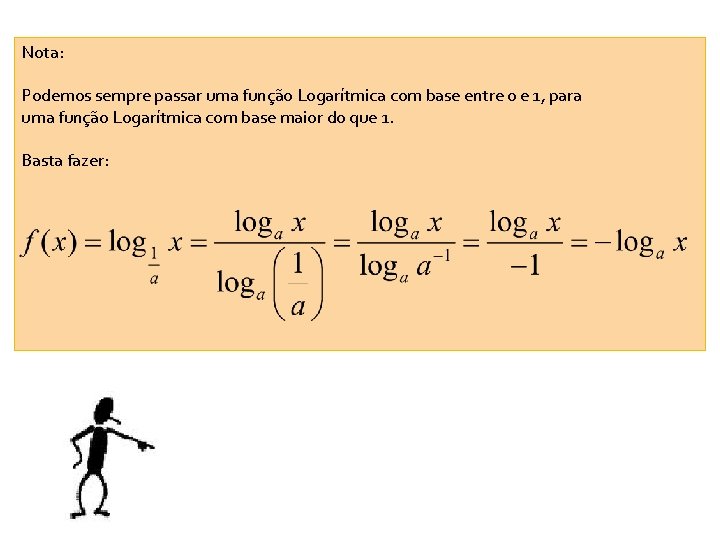
Nota: Podemos sempre passar uma função Logarítmica com base entre 0 e 1, para uma função Logarítmica com base maior do que 1. Basta fazer:

Equações com Logaritmos Importante: Cálculo do Domínio. As soluções têm que pertencer ao DOMÍNIO. Por vezes, teremos que recorrer a outras técnicas de resolução de equações: -Definição de Logaritmo -Lei do anulamento do produto - Fórmula resolvente

Inequações com Logaritmos Importante: Cálculo do Domínio. As soluções têm que pertencer ao DOMÍNIO. No final, interseta-se o conjunto solução com o conjunto do DOMÍNIO. Se a > 1 Se 0 < a < 1 Por vezes, teremos que recorrer a outras técnicas de resolução de inequações: - Quadros de sinais - resolução de inequações do 2. º grau (recurso ao gráfico)

Exercícios Manual, página 146 e 147, 22; página 147 e 148, 23

Mais limites notáveis … Recorda que: Temos agora, ainda estes:

Exercícios Manual página 150, 24 Página 151, 25 Página 153, 26

Para calcular limites de funções do tipo Atenderemos a que: Como a função exponencial é contínua: Exercícios Manual, página 153, 27; página 154, 28 e página 155, 29