Explorando a ideia de nmero positivo e nmero

Explorando a ideia de número positivo e número negativo Temperatura A unidade de medida de temperatura usada no Brasil é o grau Celsius (ºC). As medidas de temperatura maiores do que 0 ºC são as de medidas acima de zero. Dizemos que elas têm valor positivo (+3 ºC, +25 ºC, +36 ºC, etc. ). As medidas de temperaturas menores do que 0 ºC são medidas abaixo de zero. Dizemos que elas têm valor negativo (‒ 4 ºC, ‒ 9 ºC, ‒ 25 ºC, etc. ). PAULO MANZI/ARQUIVO DA EDITORA Início Sair

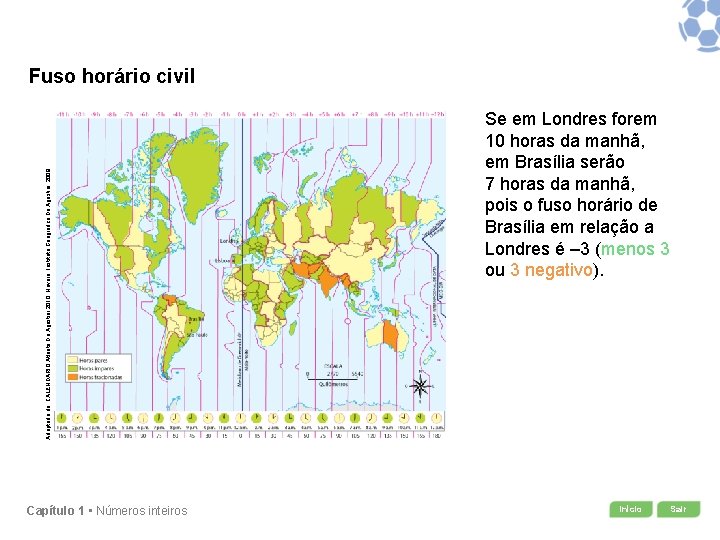
Adaptado de: CALENDARIO Atlante De Agostini 2010. Novara: Instituto Geografico De Agostini, 2009. Fuso horário civil Capítulo 1 • Números inteiros Se em Londres forem 10 horas da manhã, em Brasília serão 7 horas da manhã, pois o fuso horário de Brasília em relação a Londres é – 3 (menos 3 ou 3 negativo). Início Sair

O conjunto dos números inteiros Você já conhece do 6º ano o conjunto dos números naturais: ℕ = {0, 1, 2, 3, 4, 5, 6, . . . } ou ℕ = {0, +1, +2, +3, +4, +5, +6, . . . } Observe agora o conjunto dos números inteiros negativos: {. . . , ‒ 6, ‒ 5, ‒ 4, ‒ 3, ‒ 2, ‒ 1} Reunindo os números naturais (ℕ) com os números inteiros negativos, obtemos o conjunto dos números inteiros, que é representado assim: ℤ = {. . . , ‒ 6, ‒ 5, ‒ 4, ‒ 3, ‒ 2, ‒ 1, 0, +1, +2, +3, +4, +5, +6, . . . } Capítulo 1 • Números inteiros Início Sair

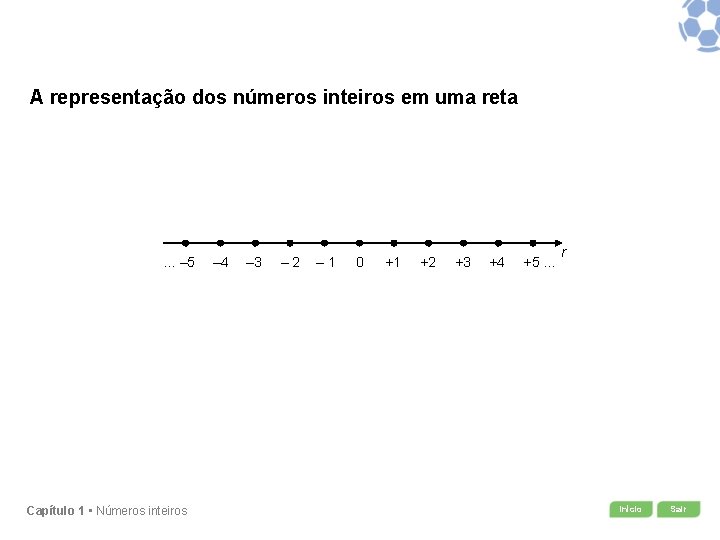
A representação dos números inteiros em uma reta . . . ‒ 5 Capítulo 1 • Números inteiros ‒ 4 ‒ 3 ‒ 2 ‒ 1 0 +1 +2 +3 +4 +5. . . r Início Sair

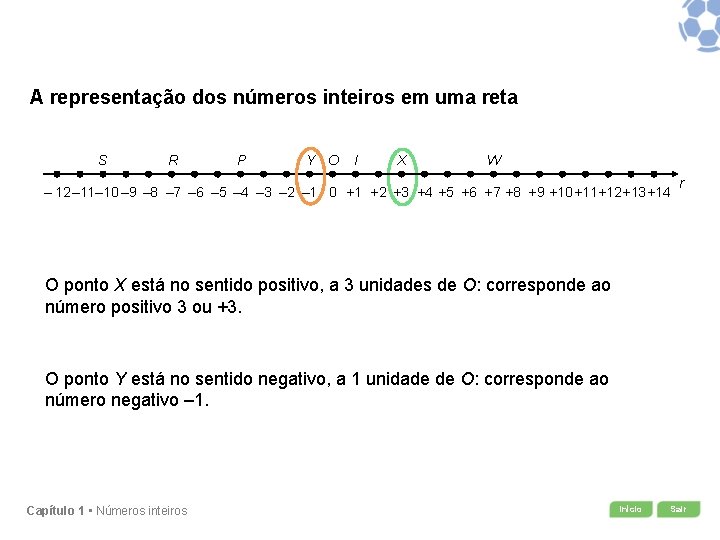
A representação dos números inteiros em uma reta S R P Y O I X W ‒ 12 ‒ 11‒ 10 ‒ 9 ‒ 8 ‒ 7 ‒ 6 ‒ 5 ‒ 4 ‒ 3 ‒ 2 ‒ 1 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11+12+13+14 r O ponto X está no sentido positivo, a 3 unidades de O: corresponde ao número positivo 3 ou +3. O ponto Y está no sentido negativo, a 1 unidade de O: corresponde ao número negativo – 1. Capítulo 1 • Números inteiros Início Sair

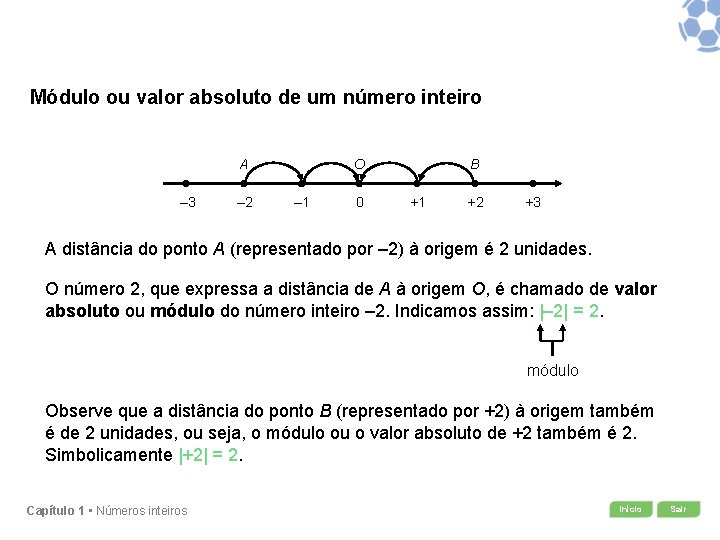
Módulo ou valor absoluto de um número inteiro A ‒ 3 ‒ 2 O ‒ 1 0 B +1 +2 +3 A distância do ponto A (representado por – 2) à origem é 2 unidades. O número 2, que expressa a distância de A à origem O, é chamado de valor absoluto ou módulo do número inteiro – 2. Indicamos assim: |– 2| = 2. módulo Observe que a distância do ponto B (representado por +2) à origem também é de 2 unidades, ou seja, o módulo ou o valor absoluto de +2 também é 2. Simbolicamente |+2| = 2. Capítulo 1 • Números inteiros Início Sair

Módulo ou valor absoluto de um número inteiro O módulo de um número diferente de zero é sempre positivo. Capítulo 1 • Números inteiros |– 3| = 3 |+9| = 9 |0| = 0 |– 20| = 20 Início Sair

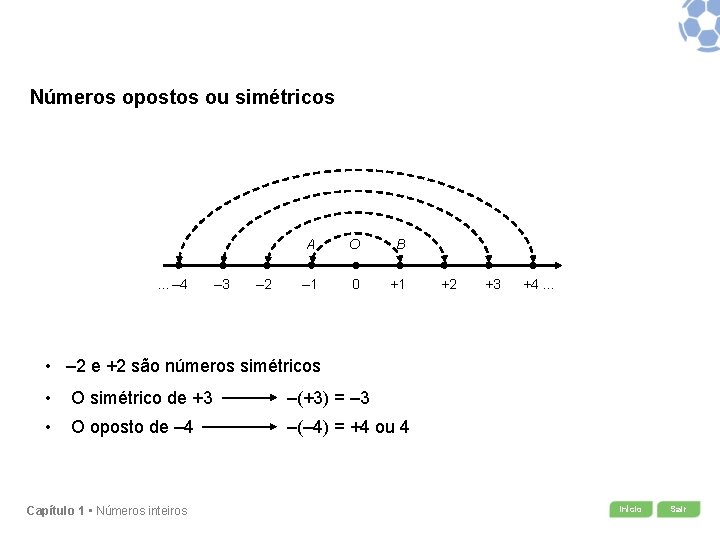
Números opostos ou simétricos . . . ‒ 4 ‒ 3 ‒ 2 A O B ‒ 1 0 +1 +2 +3 +4. . . • ‒ 2 e +2 são números simétricos • O simétrico de +3 –(+3) = ‒ 3 • O oposto de – 4 –(‒ 4) = +4 ou 4 Capítulo 1 • Números inteiros Início Sair

Comparação de números inteiros PAULO MANZI/ARQUIVO DA EDITORA Comparar dois números significa dizer se o primeiro é maior do que (>), menor do que (<) ou igual ao (=) segundo número. – 3 < +3 Qualquer número negativo é menor do que o número positivo. Capítulo 1 • Números inteiros Início Sair

PAULO MANZI/ARQUIVO DA EDITORA O menor número entre dois números negativos é aquele tem o maior módulo. – 1 > – 3 Capítulo 1 • Números inteiros Início Sair

Adição de números inteiros Somando inteiros positivos Quando as duas parcelas são positivas, o resultado da adição é sempre positivo e o módulo do resultado é obtido somando os módulos das parcelas. (+4) + (+3) = 4 + 3 = 7 ou +7 (+5) + (+6) = 5 + 6 = +11 Somando inteiros negativos Quando as duas parcelas são negativas, o resultado da adição é sempre negativo e seu módulo é obtido somando os módulos das parcelas. (– 1) + (– 3) = – 1 – 3 = – 4 Capítulo 1 • Números inteiros (– 2) + (– 1) = – 2 – 1 = – 3 Início Sair

Adição de números inteiros Somando inteiros opostos Quando as duas parcelas são dois números inteiros opostos ou simétricos, o resultado é zero. (– 4) + (+4) = – 4 + 4 = 0 (– 5) + (+5) = – 5 + 5 = 0 Somando inteiros não opostos Quando as parcelas têm sinais diferentes e não são números opostos, o sinal do resultado é o sinal do número que tem maior módulo. E o módulo do resultado é obtido subtraindo o módulo menor do módulo maior. (– 2) + (+5) = – 2 + 5 = +3 Capítulo 1 • Números inteiros (– 9) + (+3) = – 9 + 3 = – 6 Início Sair

Propriedades da adição Propriedade comutativa (– 3) + (+7) = +4 (+7) + (– 3) = +4 (– 3) + (+7) = (+7) + (– 3) Propriedade associativa [(– 7) + (+4)] + (+3) = [– 3] + (+3) = 0 [(– 7) + (+4)] + (+3) = (– 7) + [(+4) + (+3)] = (– 7) + (+7) = 0 Propriedade do elemento neutro (+5) + 0 = 0 + (+5) = +5 (– 3) + 0 = 0 + (– 3) = – 3 O zero é o elemento neutro da adição. Propriedade do elemento oposto O oposto de – 5 é +5, pois (– 5) + (+5) = 0 Capítulo 1 • Números inteiros Início Sair

Subtração de números inteiros O sinal de menos na frente do parênteses, colchetes ou chaves indica o oposto do número. (– 9) – (+2) = – 9 – 2 = – 11 o sinal de “menos” indica o oposto do +2, ou seja, – 2. (– 5) – (– 3) = – 5 + 3 = – 2 oposto de (– 3), que é +3 Capítulo 1 • Números inteiros Início Sair

Adição algébrica e soma algébrica Uma expressão numérica que contém somente as operações de adição e subtração representa uma adição algébrica. 15 – [18 – (– 6 – 9)] = 10 + {– 12 + [5 – (1 – 9)] – 7} = = 15 – [18 – (– 15)] = = 10 + {– 12 + [5 – (– 8)] – 7} = = 15 – [18 + 15] = = 10 + {– 12 + [5 + 8] – 7} = = 15 – 33 = = 10 + {– 12 + 13 – 7} = = – 18 = 10 + {– 6} = = 10 – 6 = =4 Capítulo 1 • Números inteiros Início Sair

Multiplicação de números inteiros Multiplicação com números inteiros positivos e o zero A multiplicação de dois números inteiros positivos dá como resultado um número inteiro positivo. Os módulos devem ser multiplicados. Se um dos fatores é um número inteiro e o outro é zero, o produto é zero. (+3). (+5) = +15 0. (+8) = 0 (+10). (+5) = +50 3. 5 = 15 Multiplicação de dois números inteiros com sinais diferentes Para multiplicar um número inteiro positivo por um número inteiro negativo, em qualquer ordem, multiplicamos os valores absolutos e damos ao produto o sinal negativo. (+5). (– 3) = 5. (– 3) = (– 3) + (– 3) = – 5 (– 7). (+5) = –(+35) = – 35 Capítulo 1 • Números inteiros Início Sair

Multiplicação com números inteiros negativos e o zero O resultado da multiplicação de dois números inteiros negativos é sempre positivo, e seu módulo é o produto dos módulos dois fatores. Se um dos fatores é um número inteiro e o outro é zero, o produto é zero. (– 5). (– 3) = – (+5). (– 3) = – (– 15) = +15 (– 5) = – (+5) 0. (– 8) = 0 Capítulo 1 • Números inteiros Início Sair

Propriedades da multiplicação em ℤ Propriedade comutativa (– 2). (+5) = – 10 (+5). (– 2) = – 10 (– 2). (+5) = (+5). (– 2) Propriedade associativa [(– 8). (+9)]. (+3) = (– 72). (+3) = – 216 (– 8). [(+9). (+3)] = (– 8). (+27) = – 216 [(– 8). (+9)]. (+3) = (– 8). [(+9). (+3)] Propriedade do elemento neutro (+6). (+1) = (+1). (+6) = +6 O número +1 é o elemento neutro da multiplicação. Propriedade distributiva (+3). [(+2) + (– 5)] = (+3). (+2) + (+3). (– 5) = +6 – 15 = – 9 Capítulo 1 • Números inteiros Início Sair

Divisão de números inteiros A divisão é a operação inversa da multiplicação. Se 3. 5 = 15, então 15 : 5 = 3 e 15 : 3 = 5. (+20) : (+5) = (+4) (– 30) : (– 6) = (+5) sinais diferentes (+40) : (– 5) = (– 8) Capítulo 1 • Números inteiros Não existe divisão por zero. Nem sempre é possível realizar a divisão em ℤ. Por exemplo, (– 7) : (+2) não pode ser realizada em ℤ, pois o quociente não é um número inteiro. Início Sair

Potenciação: número inteiro na base e número natural no expoente Base 0 e expoente diferente de 0 01 = 0 02 = 0. 0 = 0 Base positiva (+8)1 = +8 (+2)3 = (+2) = +8 Base negativa (– 5)1 = – 5 Quando a base é um número inteiro negativo e o expoente é um número ímpar, o sinal do resultado é negativo e seu módulo é obtido fazendo a potenciação do módulo da base. (– 6)2 = (– 6) = +36 Quando o expoente é um número par, o sinal do resultado é positivo e seu módulo é obtido fazendo a potenciação do módulo da base. Capítulo 1 • Números inteiros Início Sair

Propriedades da potenciação em ℤ Produto de potências de mesma base am. an = am + n Quociente de potências de mesma base am : an = am – n, com a ≠ 0 Potência de uma potência (am)n = am. n Potência de um produto ou de um quociente (a. b)n = an. bn Capítulo 1 • Números inteiros = , (b ≠ 0) Início Sair

Radiciação: raiz quadrada exata de um número inteiro Raiz quadrada exata dos números inteiros positivos e do zero = 3, pois 3. 3 = 9, podemos escrever = +3, pois (+3)2 = +9. é impossível em ℤ, pois não existe número inteiro que elevado ao quadrado resulte +10. A raiz quadrada de um número negativo é impossível em ℤ, pois não existe número inteiro que elevado ao quadrado resulte – 9. Capítulo 1 • Números inteiros Início Sair

Outras expressões numéricas com números inteiros (– 3 + 9 – 1 – 7)2 = : (+2) + (– 5)2. (– 4) = = (– 11 + 9)2 = = (+6) : (+2) + (+25). (– 4) = = (– 2)2 = = (+3) + (– 100) = = +4 = – 97 (– 2). [(– 3) – (– 2)] = = (– 2). [(– 3) + 2] = = (– 2). (– 1) = = +2 Capítulo 1 • Números inteiros Início Sair

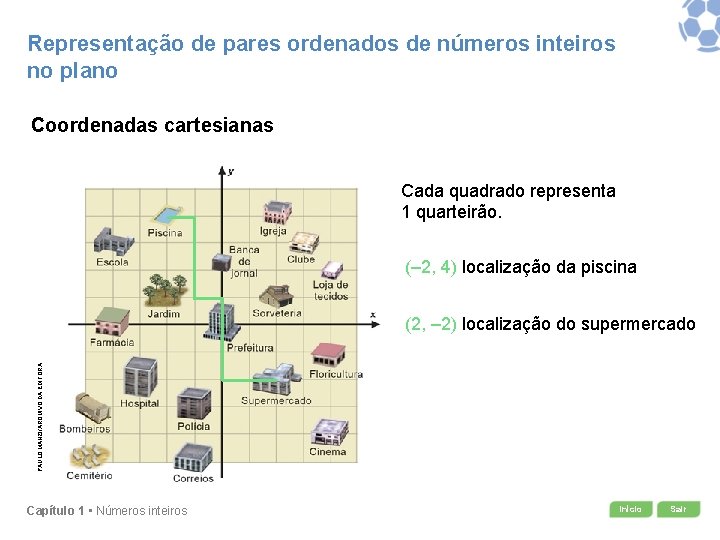
Representação de pares ordenados de números inteiros no plano Coordenadas cartesianas Cada quadrado representa 1 quarteirão. (– 2, 4) localização da piscina PAULO MANZI/ARQUIVO DA EDITORA (2, – 2) localização do supermercado Capítulo 1 • Números inteiros Início Sair