Lift Theories Linear Motion Requirements for a Valid







- Slides: 23

Lift Theories Linear Motion






Requirements for a Valid Theory 1) A valid theory is a rational explanation of observed phenomenon 2) A valid theory can be used to predict future observations 3) A valid theory produces numerical results





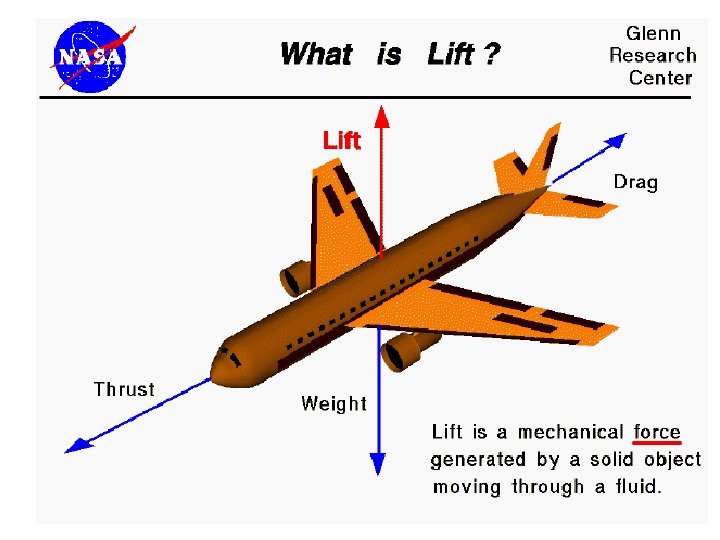
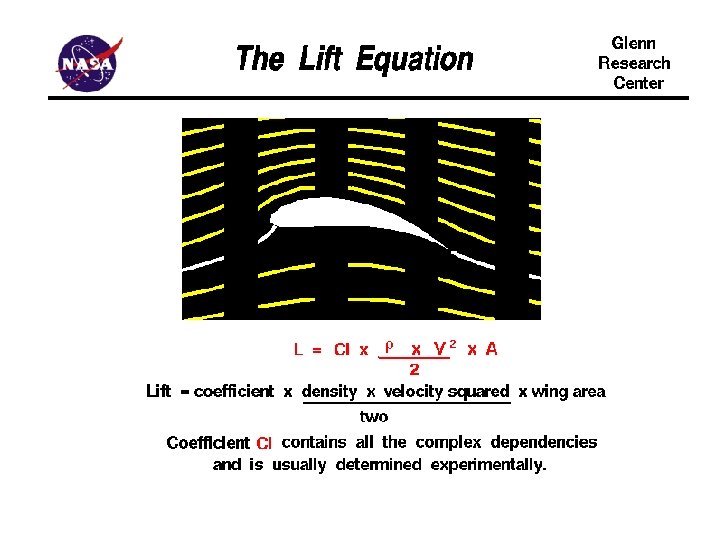
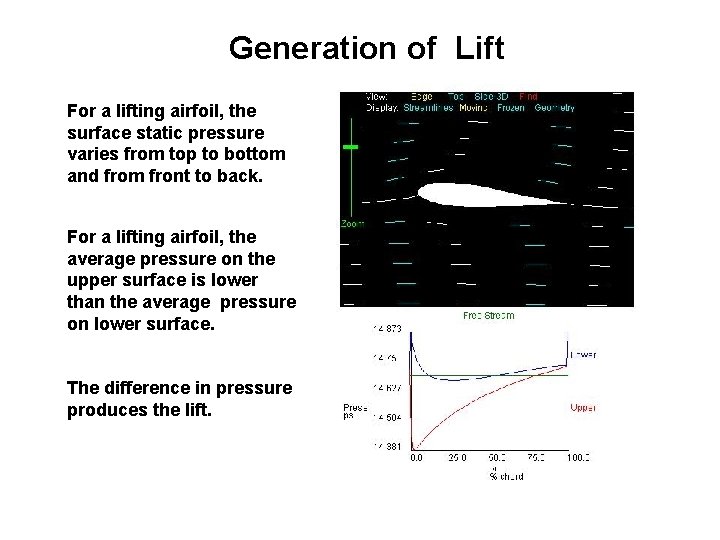
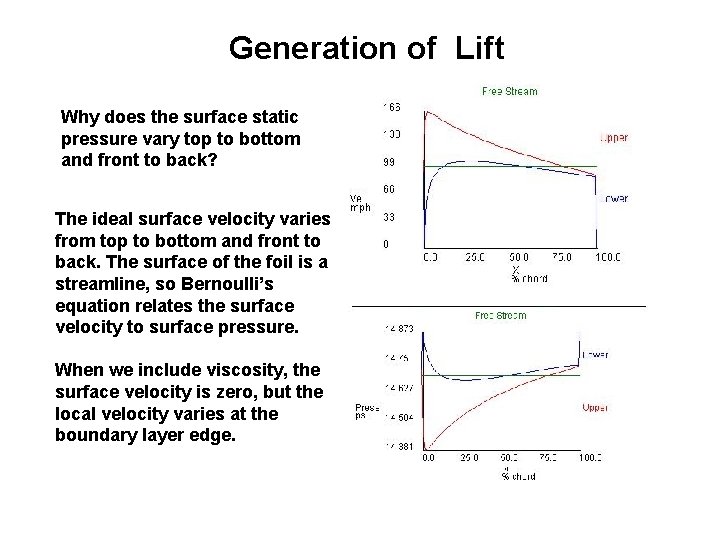
Generation of Lift For a lifting airfoil, the surface static pressure varies from top to bottom and from front to back. For a lifting airfoil, the average pressure on the upper surface is lower than the average pressure on lower surface. The difference in pressure produces the lift.

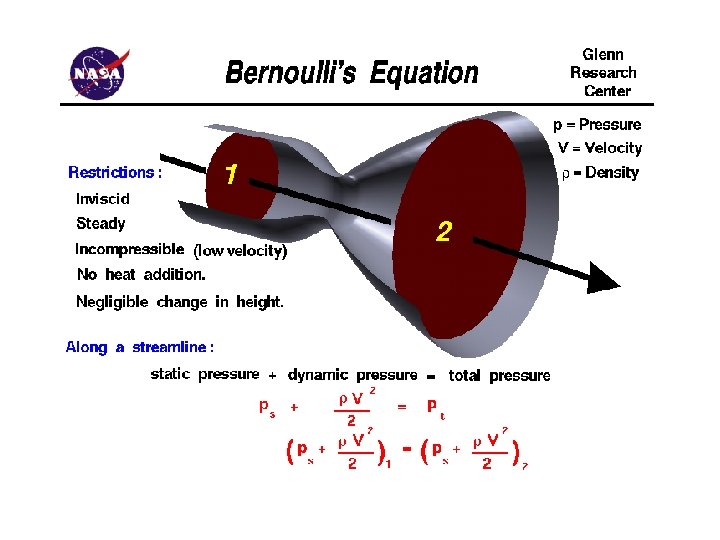
Generation of Lift Why does the surface static pressure vary top to bottom and front to back? The ideal surface velocity varies from top to bottom and front to back. The surface of the foil is a streamline, so Bernoulli’s equation relates the surface velocity to surface pressure. When we include viscosity, the surface velocity is zero, but the local velocity varies at the boundary layer edge.

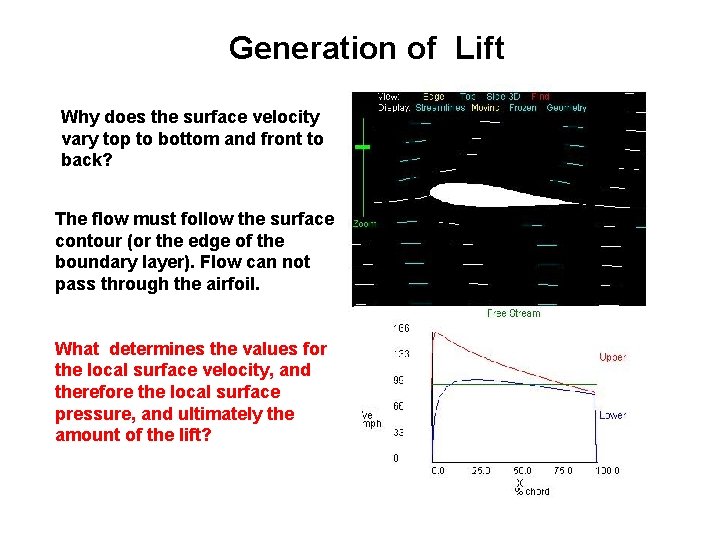
Generation of Lift Why does the surface velocity vary top to bottom and front to back? The flow must follow the surface contour (or the edge of the boundary layer). Flow can not pass through the airfoil. What determines the values for the local surface velocity, and therefore the local surface pressure, and ultimately the amount of the lift?

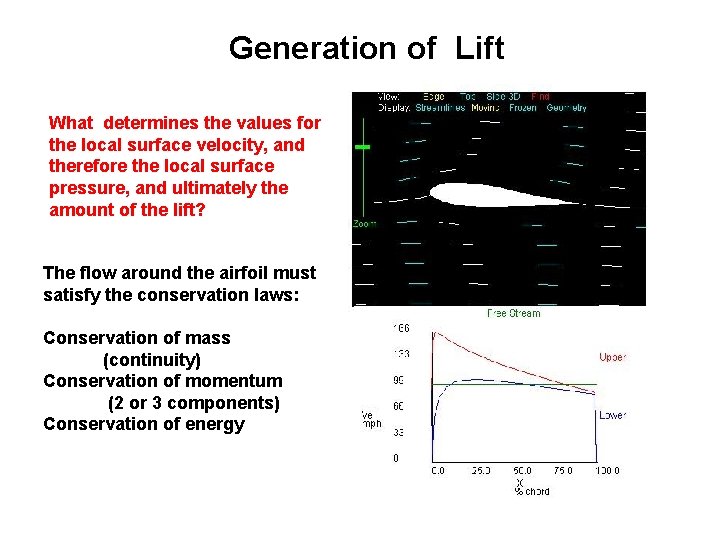
Generation of Lift What determines the values for the local surface velocity, and therefore the local surface pressure, and ultimately the amount of the lift? The flow around the airfoil must satisfy the conservation laws: Conservation of mass (continuity) Conservation of momentum (2 or 3 components) Conservation of energy


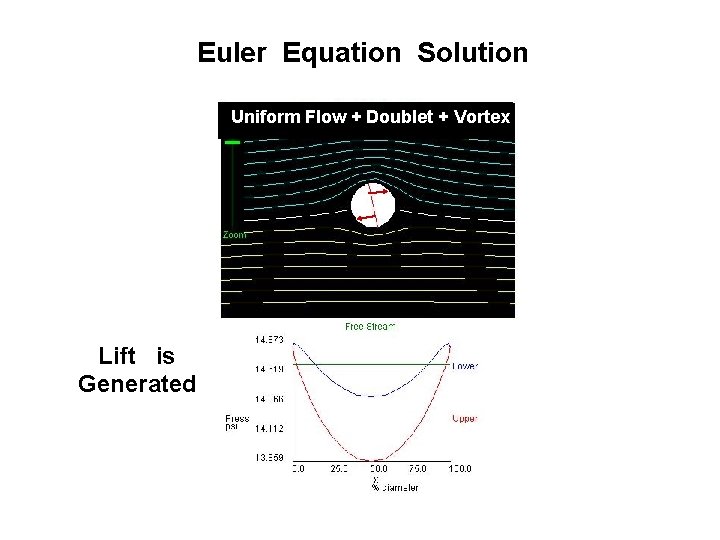
Euler Equation Solution Uniform Flow + Doublet + Vortex Lift is Generated

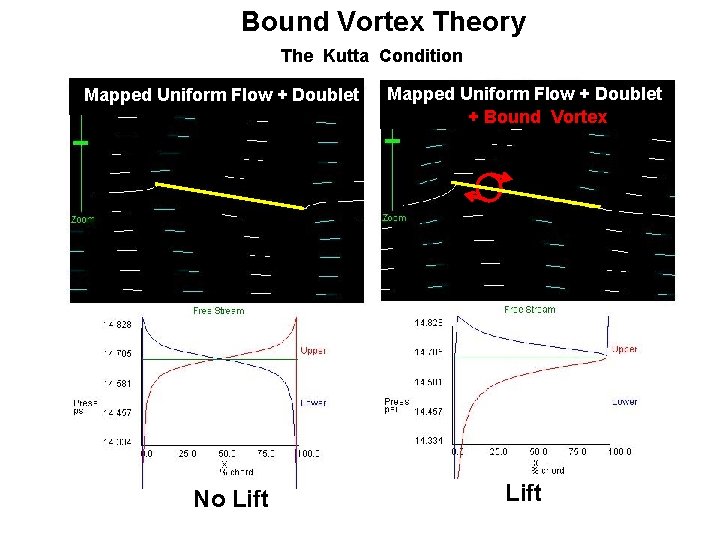
Bound Vortex Theory The Kutta Condition Mapped Uniform Flow + Doublet No Lift Mapped Uniform Flow + Doublet + Bound Vortex Lift

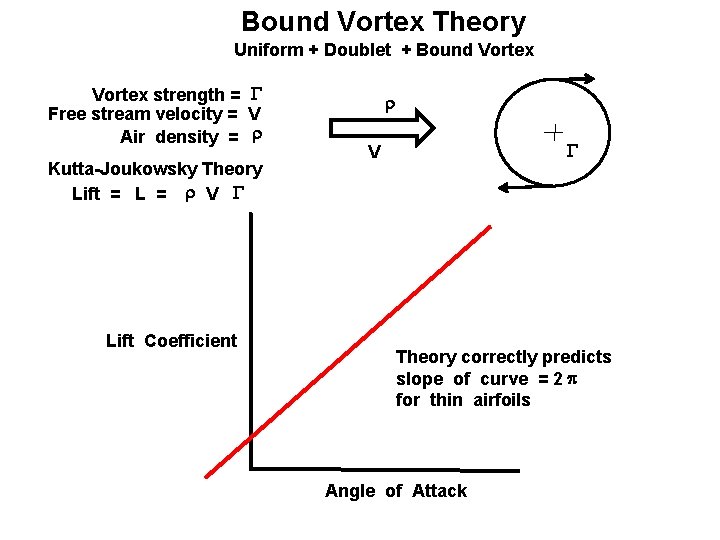
Bound Vortex Theory Uniform + Doublet + Bound Vortex strength = G Free stream velocity = V Air density = r Kutta-Joukowsky Theory Lift = L = r V G Lift Coefficient r G V Theory correctly predicts slope of curve = 2 p for thin airfoils Angle of Attack

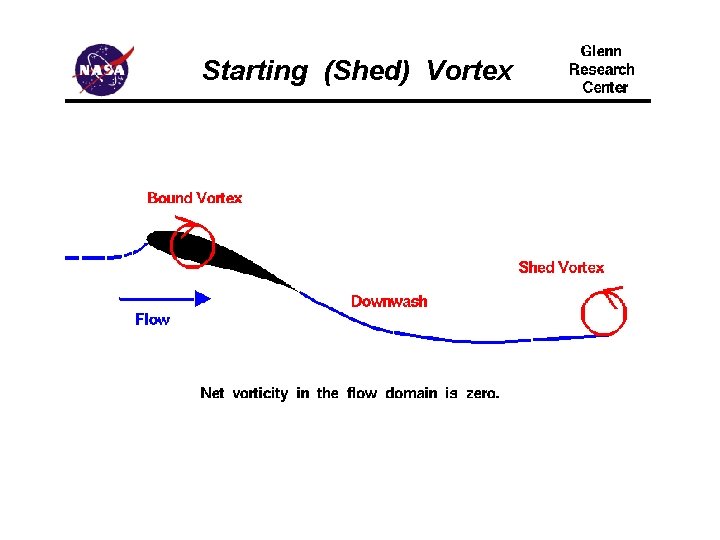
Starting (Shed) Vortex

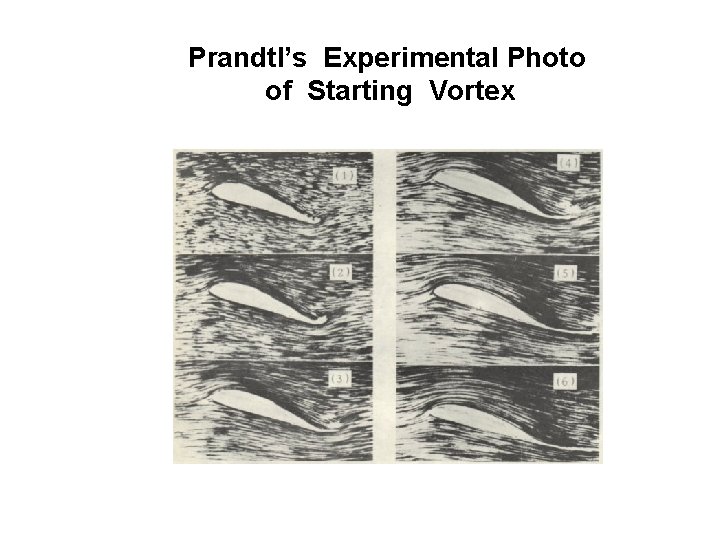
Prandtl’s Experimental Photo of Starting Vortex

Prandtl Lifting Line Theory Bound Vortex Tip Vortex Three dimensional version of Bound Vortex Theory A continuous line of bound vortices terminating at the wing tips with “tip vortices” that continue downstream to the “starting vortex”.

Photo of Tip Vortices