Representing Motion Linear motion motion in a single

Representing Motion Linear motion: motion in a single dimension (in a line). A rate tells how quickly something happens. Rate: A quantity divided by time

Motion is Relative Frame of Reference: point of view of the observer – If something is relative, it depends on the frame of reference. – When we discuss the motion of something, we describe its motion relative to something else. • Usually, when we discuss the speeds of things on Earth, we mean the speed with respect to the Earth’s surface.

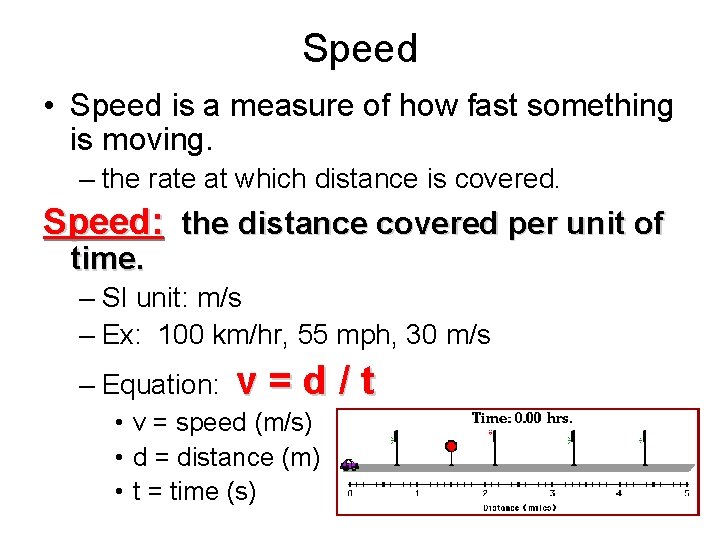
Speed • Speed is a measure of how fast something is moving. – the rate at which distance is covered. Speed: the distance covered per unit of time. – SI unit: m/s – Ex: 100 km/hr, 55 mph, 30 m/s – Equation: v=d/t • v = speed (m/s) • d = distance (m) • t = time (s)

Instantaneous speed • the speed at any given instant – Ex: speedometer Average speed • the total distance covered divided by the time interval • Average speed does not indicate changes in the speed that may take place during a trip. BOTH instantaneous and average speeds indicate the rate at which distance is covered.

Physics Problem Solving Strategy 1. List your variables 1. Givens 2. Unknown variable 2. If need be, convert variables to SI units 3. Choose the equation that matches your variables 4. Substitute variables in to the equation 5. Solve

Check Your Understanding If a cheetah can maintain a constant speed of 25 m/s, it covers 25 meters every second. At this rate, how far will it travel in 10 seconds? üd = ? v = 25 m/s t = 10 s v = d /t 25 m/s = (d) / (10 s) d = (25 m/s)(10 s) d = 250 m

Check Your Understanding In one minute? üd = ? v = 25 m/s t = 60 s **Convert minutes seconds** v=d/t 25 m/s = (d) / (60 s) d = (25 m/s)(60 s) d = 1500 m

Velocity • When we say that a car travels 60 km/hr, we are indicating it’s speed. When we say that a car is traveling 60 km/hr to the north, we are indicating it’s velocity. Velocity: the speed in a given direction • SI unit: m/s • Ex: 100 km/hr East, 55 mph North, 30 m/s Southwest • Equation: v=d/t • Speed is a description of how fast an object moves; velocity is how fast it moves AND in what direction.

Check Your Understanding The speedometer of a car moving northward reads 100 km/h. It passes another car that travels southward at 100 km/h. Do both have the same speed? Do they have the same velocity? ü Both cars have the same speed, but they have opposite velocities because they are moving in opposite directions.

Constant Velocity • Constant velocity requires both constant speed and constant direction. • Motion at constant velocity is in a straight line at constant speed. Changing Velocity • Constant speed and constant velocity are not the same thing. • A body may move with constant speed around a curved path, but it does not move with constant velocity because the direction changes at every instant.

Vector and Scalar Quantities • Scalar: a quantity that requires magnitude only – Number and units ONLY – Ex: Speed, mass, time • Vector: a quantity that requires both magnitude AND direction – Number, units, AND direction – Ex: Velocity, acceleration, force

Check Your Understanding Is height a scalar or vector quantity? ü Scalar. Height only includes magnitude (how big the number is) only and NOT direction. You are 5’ 8” tall, not 5’ 8” to the east.

Adding Vectors • An arrow is used to represent the magnitude & direction of a vector quantity. – The length of the arrow indicates the magnitude of the vector quantity. – The direction of the arrow represents the direction of the vector quantity. • When more than one vector combines together, both the magnitude AND the direction matter. • The sum of 2 or more vectors is called the resultant.

1. Arrows that point in the same direction are added together to find the resultant. – 4 m/s N + 3 m/s N = 7 m/s 2. Arrows that point in opposite directions are subtracted to find the resultant. – 4 m/s N – 3 m/s S = 1 m/s 3. When arrows are at right angles to each other, the diagonal of a rectangle will determine the resultant. – Use the Pythagorean theorem: a 2 + b 2 = c 2 – (4 m/s N)2 + (3 m/s E)2 = 16 + 9 = 25 = (5 m/s NE)2

Check Your Understanding A boy is riding his bike down the street at a speed of 10 m/s. A gust of wind came out of nowhere headed towards the boy. If the wind is traveling 3 m/s, what will the boy’s new speed be? ü Since the boy and the wind are moving in opposite directions, we need to subtract their speeds to find the resultant. 10 m/s – 3 m/s = 7 m/s

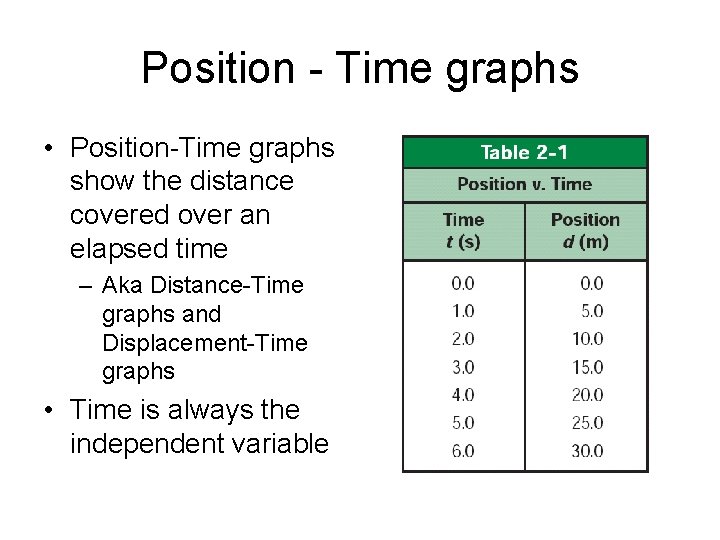
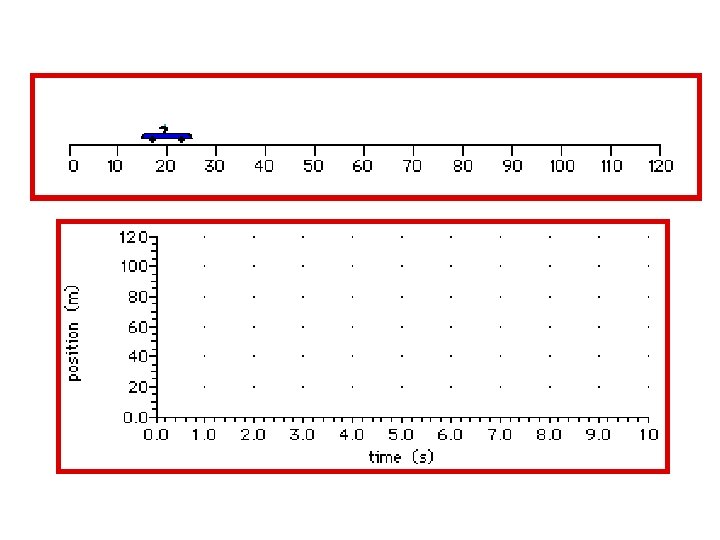
Position - Time graphs • Position-Time graphs show the distance covered over an elapsed time – Aka Distance-Time graphs and Displacement-Time graphs • Time is always the independent variable

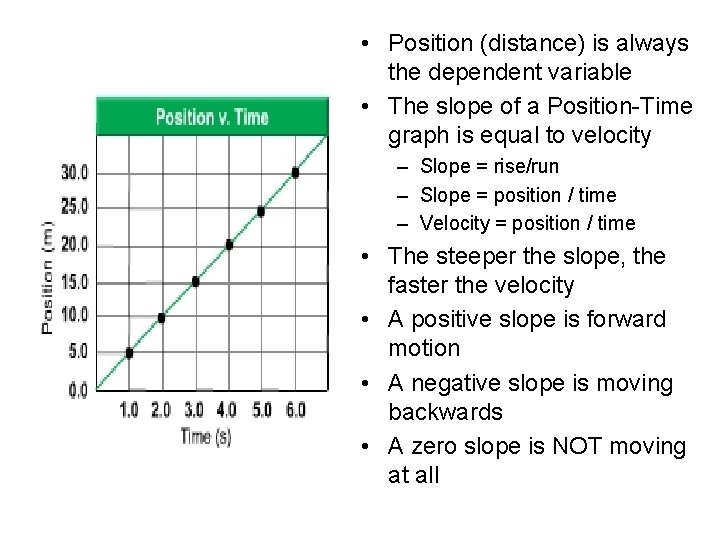
• Position (distance) is always the dependent variable • The slope of a Position-Time graph is equal to velocity – Slope = rise/run – Slope = position / time – Velocity = position / time • The steeper the slope, the faster the velocity • A positive slope is forward motion • A negative slope is moving backwards • A zero slope is NOT moving at all

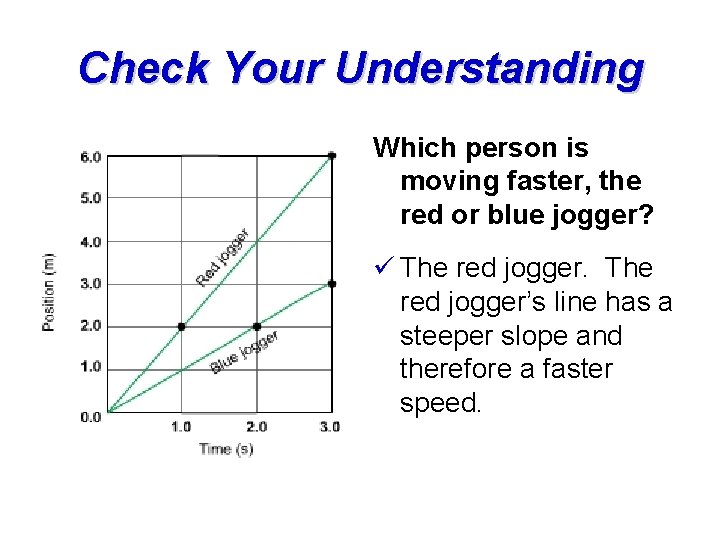
Check Your Understanding Which person is moving faster, the red or blue jogger? ü The red jogger’s line has a steeper slope and therefore a faster speed.

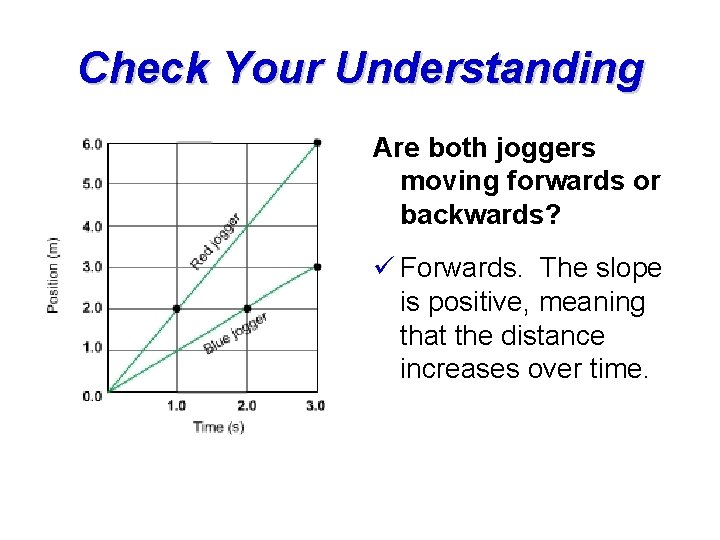
Check Your Understanding Are both joggers moving forwards or backwards? ü Forwards. The slope is positive, meaning that the distance increases over time.

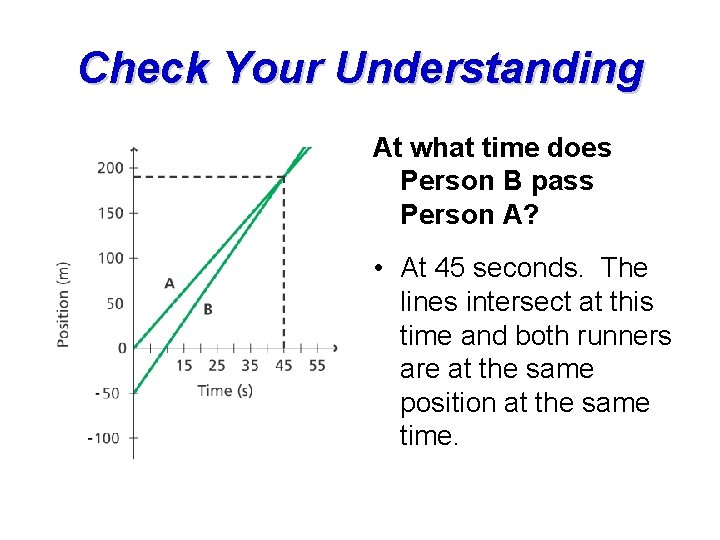
Check Your Understanding At what time does Person B pass Person A? • At 45 seconds. The lines intersect at this time and both runners are at the same position at the same time.