LESSON 4 2 MULTIPLE LINEAR REGRESSION SEMIPARTIAL AND

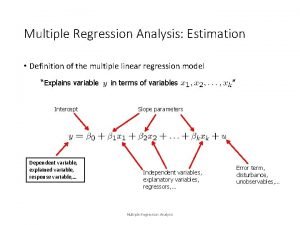
LESSON 4. 2. MULTIPLE LINEAR REGRESSION. SEMIPARTIAL AND PARTIAL CORRELATION Design and Data Analysis in Psychology II Susana Sanduvete Chaves Salvador Chacón Moscoso 1

SEMIPARTIAL CORRELATION • Example: 2

SEMIPARTIAL CORRELATION • Example: Because X 1 and X 2 correlate 3

SEMIPARTIAL CORRELATION Y Semipartial correlation a X 1 b c X 2 When X 2 is included, R 2 increases 0. 15 4

SEMIPARTIAL CORRELATION • The order in which the independent variables are included in the model, influences the results. Example: – X 1 is included firstly: – X 2 is included firstly: It is explained by X 2 It is explained by X 1 5

SEMIPARTIAL CORRELATION • The variable will explain less from the model: – As more correlated is with other variables. – As later it is introduced. • There are no rules to specify the entrance order. Usual criterion: The first variable is which presents the highest r. XY (in the example, X 1 would be the first one because r. Y 1 > r. Y 2) 6

MULTIPLE SEMIPARTIAL CORRELATION (MORE THAN TWO INDEPENDENT VARIABLES) Y Y X 1 X 3 X 4 X 2 X 3 X 2 7

Exercise 1 about semipartial correlation (February 1999, ex. 3) The variable intelligence (X 1) explains the 55% of the variability of scholar performance. When hours studied (X 2) is included, the explained variability is the 90%. Using this information and what you have in the following Venn diagram: 8

Exercise 1 about semipartial correlation Y 0. 3 X 1 X 2 • Calculate r 12, ry 1, ry 2, Ry(1. 2), Ry(2. 1) • Complete de Venn diagram 9

Exercise 2 about semipartial correlation Taking into account the following data: Calculate 10

STATISTIC SIGNIFICANCE OF THE SEMIPARTIAL CORRELATION COEFFICIENT Example: significance of k 1 = 2 theoretical. F= F(α, k-k 1, N-k-1) 11

STATISTIC SIGNIFICANCE OF THE SEMIPARTIAL CORRELATION COEFFICIENT Example: ¿ is significant in the model? 12

STATISTIC SIGNIFICANCE OF THE SEMIPARTIAL CORRELATION COEFFICIENT F(0. 05, 2, 6) = 5. 14 – H 0 13

PARTIAL CORRELATION Definition of the partial correlation squared: Proportion of shared variability by Xi and Y, having ruled out Xk variability completely. 14

PARTIAL CORRELATION • Amount of variability shared by X 1 and Y, having ruled out X 2: • Amount of variability shared by X 2 and Y having ruled out X 1: 15

PARTIAL CORRELATION: EXAMPLE Y a X 1 b 0. 1 c X 2 Partial correlations 16

PARTIAL CORRELATION: EXAMPLE 17

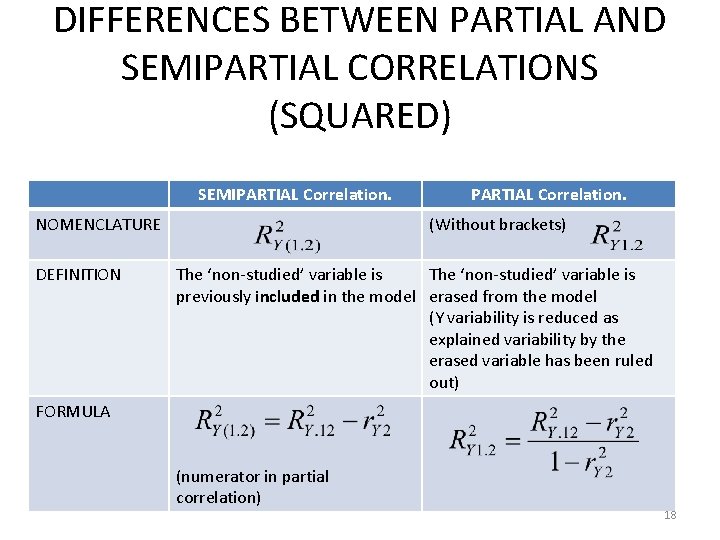
DIFFERENCES BETWEEN PARTIAL AND SEMIPARTIAL CORRELATIONS (SQUARED) SEMIPARTIAL Correlation. NOMENCLATURE DEFINITION PARTIAL Correlation. (Without brackets) The ‘non-studied’ variable is previously included in the model erased from the model (Y variability is reduced as explained variability by the erased variable has been ruled out) FORMULA (numerator in partial correlation) 18