Lecture 6 Minimum Spanning Tree 1 The Minimum

Lecture 6 Minimum Spanning Tree 1. The Minimum Spanning Tree Problem 2. Greedy algorithms 3. A Generic Algorithm 4. Kruskal’s Algorithm 5. Prim’s Algorithm 2022/1/22 2004 SDU

An Application In the design of networking Given n computers, we want to connect them so that each pair of them can communicate with each other. Every foot of cable costs us $1 We want the cheapest possible network. In the design of electronic circuitry Given n pins that should be electrically equivalent by wiring them together To interconnect a set of n pins, n-1 wires can be used, each connecting two pins We want the least possible length of wire to save cost 2004 SDU 2

Minimum Spanning Tree-The Definition Given a connected undirected graph G = (V, E) and a weight w(e) to each edge e of G, a minimum spanning tree T of G is a spanning tree with minimum total edge weight Note: (1). A spanning tree of a graph is a tree that connects all vertices. (2). A connected undirected graph may have many different spanning trees (3). The minimum spanning tree may not be unique 2004 SDU 3

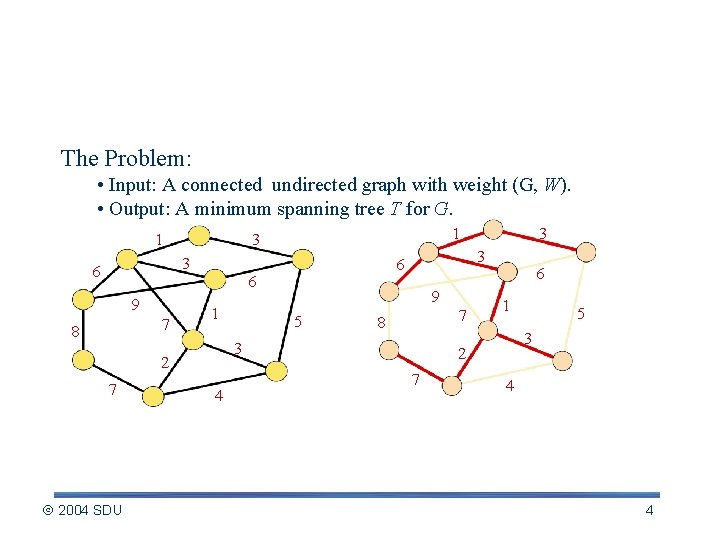
Minimum Spanning Tree Problem The Problem: • Input: A connected undirected graph with weight (G, W). • Output: A minimum spanning tree T for G. 1 3 6 9 7 8 1 2004 SDU 9 5 7 8 3 4 3 3 6 6 2 7 1 3 6 1 3 2 7 5 4 4

Greedy Algorithms A greedy algorithm always makes the choice that looks best at the moment. It makes a local optimal choice in the hope that this choice will lead to a globally optimal solution. Greedy algorithms yield optimal solutions for many (but not all) problems. 2004 SDU Page 5 5

The 0 -1 Knapsack problem The 0 -1 knapsack problem: N items, where the i-th item is worth vi dollars and weight wi pounds. 11 p 3 p 4 p 58 p 8 p 88 p § vi and wi are integers. 3$ 6$ 35$ 8$ 28$ 66$ The thief can carry at most W (integer) pounds. How to take as valuable a load as possible. § An item cannot be divided into pieces. The fractional knapsack problem: W The same setting, but the thief can take fractions of items. W may not be integer. 2004 SDU Page 6 6

Solve the fractional Knapsack problem: Greedy on the value per pound vi/wi. § Each time, take the item with maximum vi/wi. § If exceeds W, take fractions of the item. Example: (1, 5$), (2, 9$), (3, 12$), (3, 11$) and w=4. vi/wi : 5 4. 0 3. 667 First: (1, 5$), Second: (2, 9$), Third: 1/3 (3, 12$) Total W: 1, 3, 4. Can only take part of item 2004 SDU Page 7 7

Proof of correctness: (The hard part) Let X = i 1, i 2, …ik be the optimal items taken. • Consider the item j : (vj, wj) with the highest v /w. • if j is not used in X (the optimal solution), get rid of some items with total weight wj (possibly fractional items) and add item j. (since fractional items are allowed, we can do it. ) § Total value is increased. Why? § One more item selected by greedy is added to X Repeat the process, X is changed to contain all items selected by greedy WITHOUT decreasing the total value taken by the thief. 2004 SDU Page 8 8

The 0 -1 knapsack problem cannot be solved optimally by greedy Counter example: W=10 2 1. 8 Items found (6 pounds, 12 dollars), (5 pounds, 9 dollar), 1. 8 1 1 (5 pounds, 9 dollars), (3 pounds, 3 dollars), (3 pounds, 3 dollars) If we first take (6, 12) according to greedy algorithm, then solution is (6, 12), (3, 3) (total value is 12+3=15). However, a better solution is (5, 9), (5, 9) with total value 18. Note: To show that a statement does not hold, we only have to give an example. 2004 SDU Page 9 9

Greedy algorithm analysis Ingredients of greedy algorithm for solving a problem: § Greedy-choice property: a global optimal solution can be arrived at by making a locally optimal(greedy) choice. (fractional knapsack yes, 01 knapsack no ) § Optimal substructure: an optimal solution to the problem contains within it optimal solutions to sub-problems. (both fractional and 0 -1 knapsack yes) Correctness proof § Inductively prove that after each step of the greedy algorithm, its solution is at least as good as any other algorithm’s. (Huffman code) § Gradually transform any solution to the one found by the greedy algorithm. (Fractional knapsack) § Discover a simple “structural” bound asserting that any possible solution must have a certain value (lower bound). Then show that the greedy algorithm always achieves that bound. (Interval partitioning) 2004 SDU 10

Idea of the Generic Algorithm for MST It grows the minimum spanning tree one edge at a time. § The algorithm manages a set of edges A, maintaining the following loop invariant: – Prior to each iteration, A is a subset of some minimum spanning tree. An edge (u, v) is a safe edge for A if A {(u, v)} is also a subset of a minimum spanning tree, that is, § 2004 SDU (u, v) can be correctly added to A without violating the invariant 11

Genetic algorithm Kruskal’s and Prim’s algorithms are implementations of the generic algorithm on how to maintain A and find the safe edge (u, v) for A. At any time, edges of Kruskal’s form some trees, and (u, v) is the least edge between these trees Edges of Prim’s form one tree, and (u, v) is the least connecting the tree and other vertices. Safe edge is the greedy choice. At any time, the subproblem is the graph obtained by contracting any component of A as a vertex. The problem has both greedy-choice property and optimal-substructure property. 2004 SDU 12

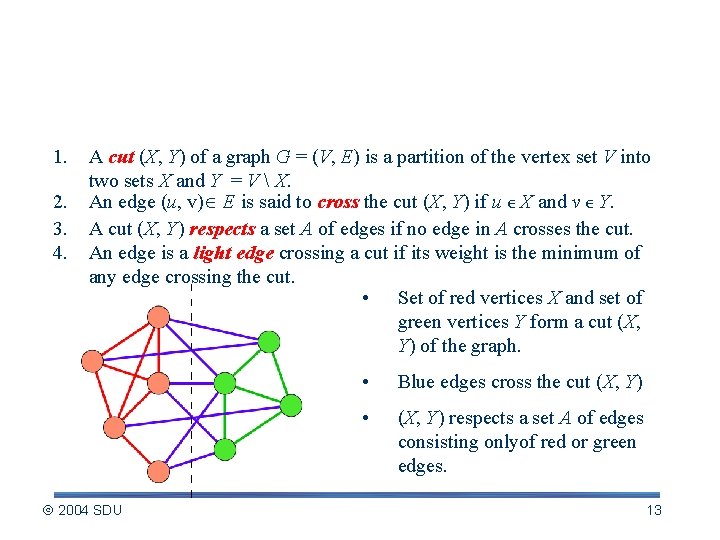
Related Notions 1. 2. 3. 4. A cut (X, Y) of a graph G = (V, E) is a partition of the vertex set V into two sets X and Y = V X. An edge (u, v) E is said to cross the cut (X, Y) if u ∈ X and v ∈ Y. A cut (X, Y) respects a set A of edges if no edge in A crosses the cut. An edge is a light edge crossing a cut if its weight is the minimum of any edge crossing the cut. • Set of red vertices X and set of green vertices Y form a cut (X, Y) of the graph. 2004 SDU • Blue edges cross the cut (X, Y) • (X, Y) respects a set A of edges consisting onlyof red or green edges. 13

Determine Safe Edges for A Theorem 23. 1 § Let G = (V, E) be a connected, undirected graph with real -valued weight function w defined on E. Let A be a subset of E that is included in some minimum spanning tree for G, let (X, Y) be any cut of G that respects A, and let (u, v) be a light edge crossing (X, Y). Then, edge (u, v) is safe for A. 2004 SDU 14

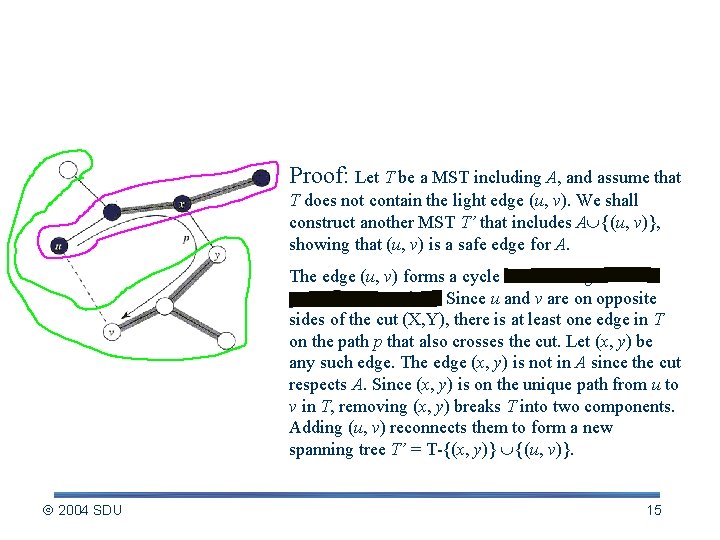
The Proof of Theorem 23. 1 Proof: Let T be a MST including A, and assume that T does not contain the light edge (u, v). We shall construct another MST T’ that includes A {(u, v)}, showing that (u, v) is a safe edge for A. The edge (u, v) forms a cycle with the edges on the path from u to v in T. Since u and v are on opposite sides of the cut (X, Y), there is at least one edge in T on the path p that also crosses the cut. Let (x, y) be any such edge. The edge (x, y) is not in A since the cut respects A. Since (x, y) is on the unique path from u to v in T, removing (x, y) breaks T into two components. Adding (u, v) reconnects them to form a new spanning tree T’ = T-{(x, y)} {(u, v)}. 2004 SDU 15

A Corollary 23. 2 § Let G = (V, E) be a connected, undirected graph with real -valued weight function w defined on E. Let A be a subset of E that is included in some minimum spanning tree for G, and let C = (VC, EC) be a connected component in the forest GA = (V, A). If (u, v) is a light edge connecting C to some other component in GA, then (u, v) is safe for A. Note: Kruskal’s and Prim’s algorithms are based on the corollary. 2004 SDU 16

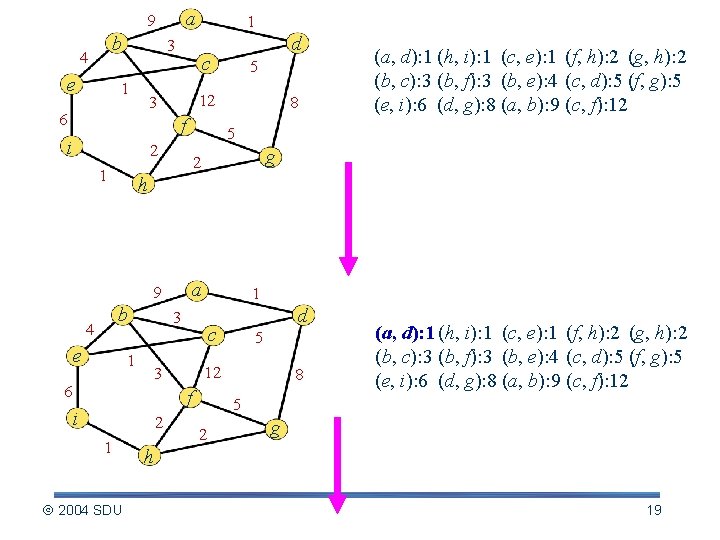
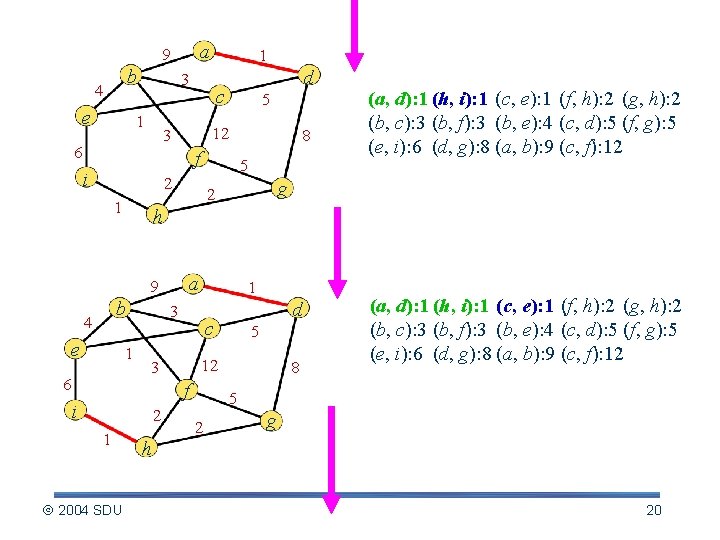
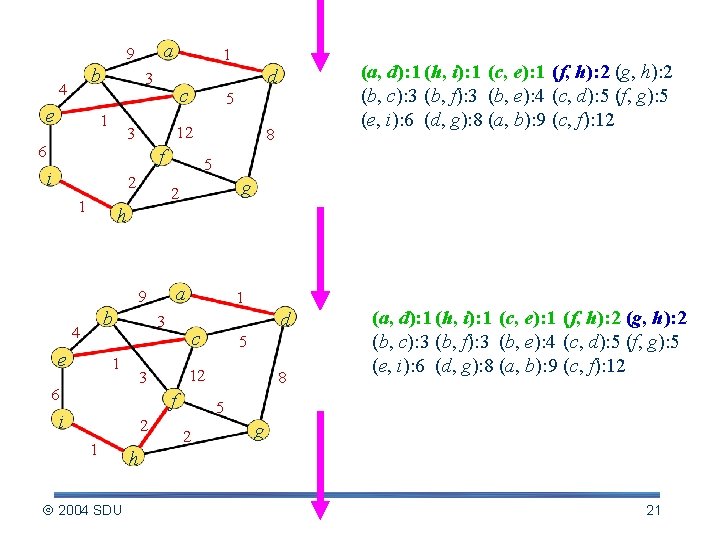
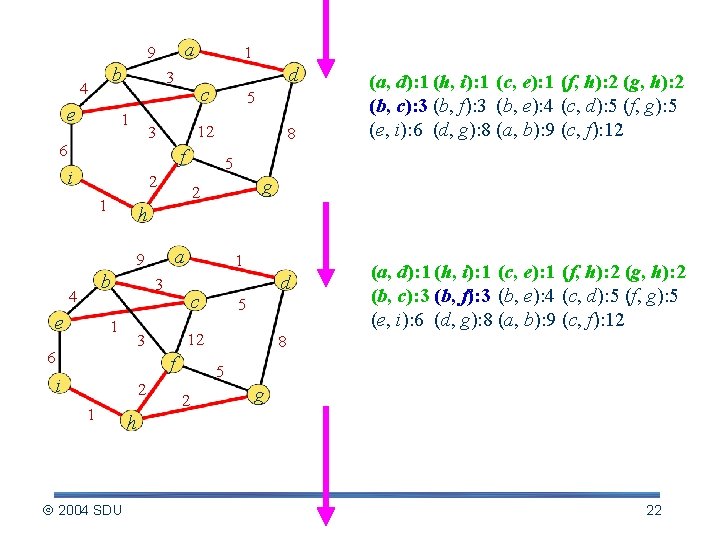
Idea of the Kruskal’s 1. Initialize the forest, each vertex as a tree, A . 2. Find the least weight edge (u, v) that connects any two trees in the forest. 3. Add (u, v) to A and make the two tree as one tree, number of trees in the forest decreases 1. 4. Repeat step 2 and 3 until A forms a spanning tree. 2004 SDU 17

Kruskal’s Algorithm 2004 SDU 18

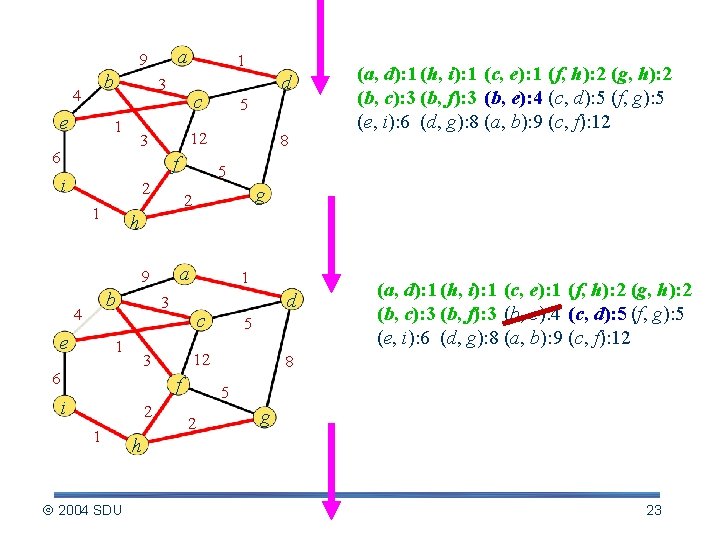
a 9 b 4 e 1 3 1 c f i g 2 h a 9 b 4 8 (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 5 2 1 5 12 3 6 d e 1 3 1 c f i 2 1 2004 SDU 5 12 3 6 d 8 (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 5 2 g h 19

a 9 b 4 e 1 3 1 c 5 12 3 6 d f i 5 2 1 b e 1 6 a 1 3 2 2004 SDU 5 12 3 i d c f 1 g 2 h 9 4 8 (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 5 2 g h 20

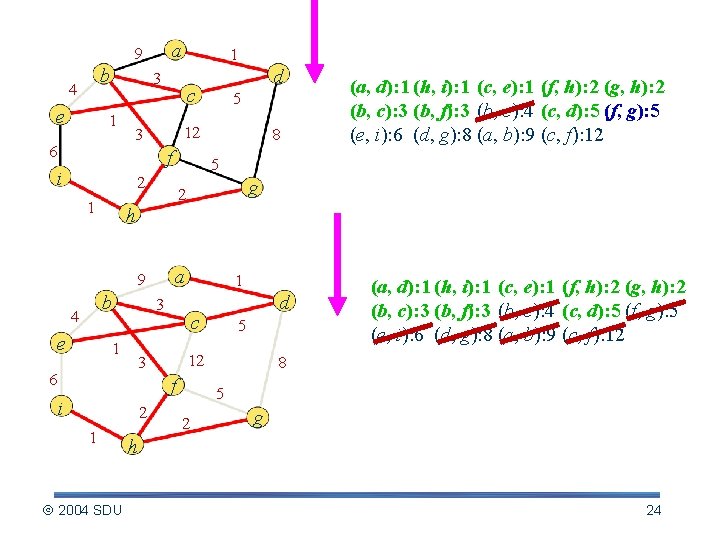
a 9 b 4 e 1 3 1 c 6 5 12 3 f i 2 1 (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 d 8 5 g 2 h a 9 b 4 e 1 6 1 3 c f 2 1 2004 SDU 5 12 3 i d 8 (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 5 2 g h 21

a 9 b 4 e 1 3 1 c 5 12 3 6 d 8 f i 5 2 1 b e g 2 h a 9 4 (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 1 3 1 c f i 2 1 2004 SDU 5 12 3 6 d (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 8 5 2 g h 22

a 9 b 4 e 1 3 1 6 c f h b e g 2 a 9 4 8 (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 5 2 1 5 12 3 i d 1 3 1 c f i 2 1 2004 SDU 5 12 3 6 d (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 8 5 2 g h 23

a 9 b 4 e 1 3 1 6 c f h b e g 2 a 9 4 8 (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 5 2 1 5 12 3 i d 1 6 1 3 c f 2 1 2004 SDU 5 12 3 i d (a, d): 1 (h, i): 1 (c, e): 1 (f, h): 2 (g, h): 2 (b, c): 3 (b, f): 3 (b, e): 4 (c, d): 5 (f, g): 5 (e, i): 6 (d, g): 8 (a, b): 9 (c, f): 12 8 5 2 g h 24

Time Complexity Analysis 1. O(V 2+Elg. V) when disjoint-set data structure are not used. • • 2. Keep two arrays: c[u]: The component name of vertex u v[c]: The vertices in component c, is a list //O(1), total (E) • FIND-SET(u): Checks c[u] • Union (u, v): Append list c[v] at the end of list c[u], and for each vertex in c[v], define c[] as c[u]. //O(V), total O(V 2) When use disjoint-set data structure with union-by-rank • Keep two arrays: p[u]: parent of u in the min-tree • rank[u]: height of tree rooted at u • FIND-SET (u): if p[u] = u, return u; else FIND-SET (p[u]); // O(lg. V) • Union (u, v): if rank (FIND-SET(u)) > rank (FIND-SET(v)), p [FINDSET(v)]=FIND-SET(u); if rank (FIND-SET(u)) < rank(FIND-SET(v)), p[FIND-SET(u)]=FIND-SET(v); else p[FIND-SET(u)]=FIND-SET(v), rank[FIND-SET(v)]++; //O(1), total (V) So total time is: O(Elg. V) 2004 SDU u v 25

Correctness 1. At any time, A is a subset of a MST 2. In the end, A is a MST Proof of 1. By induction on |A|. • Base case A 0, of course true. • Suppose 1 is true for Ak-1. Suppose the kth edge added to A is ek=(u, v). W. L. O. G, suppose u C, C is a connected component of G(V, Ak-1). Since (u, v) is the smallest remaining edge, it must be a light edge connecting C to all other components of G(V, Ak-1), so, it is safe for Ak-1, and hence Ak is subset of a MST.

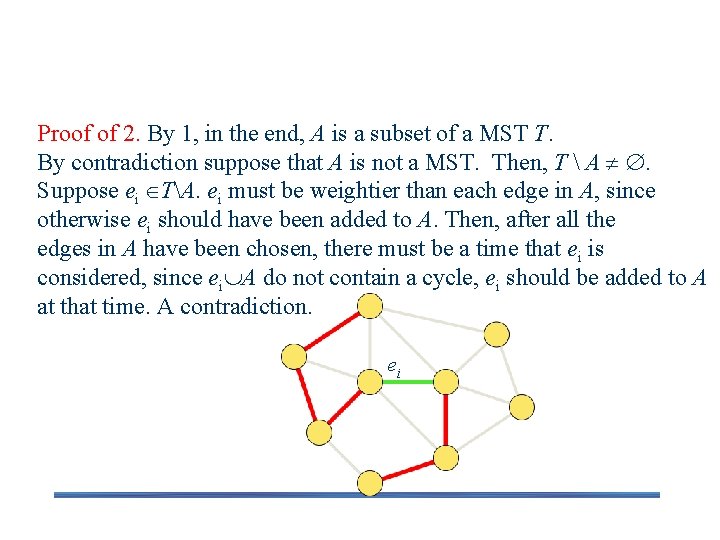
Correctness (cont. ) Proof of 2. By 1, in the end, A is a subset of a MST T. By contradiction suppose that A is not a MST. Then, T A . Suppose ei TA. ei must be weightier than each edge in A, since otherwise ei should have been added to A. Then, after all the edges in A have been chosen, there must be a time that ei is considered, since ei A do not contain a cycle, ei should be added to A at that time. A contradiction. ei

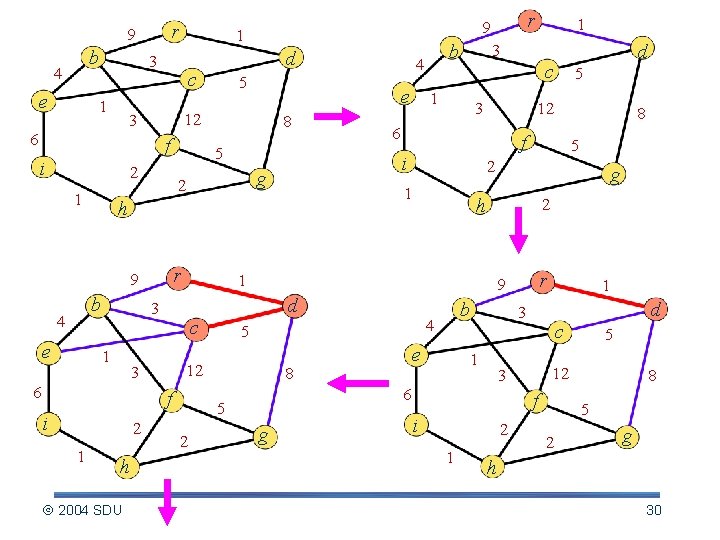
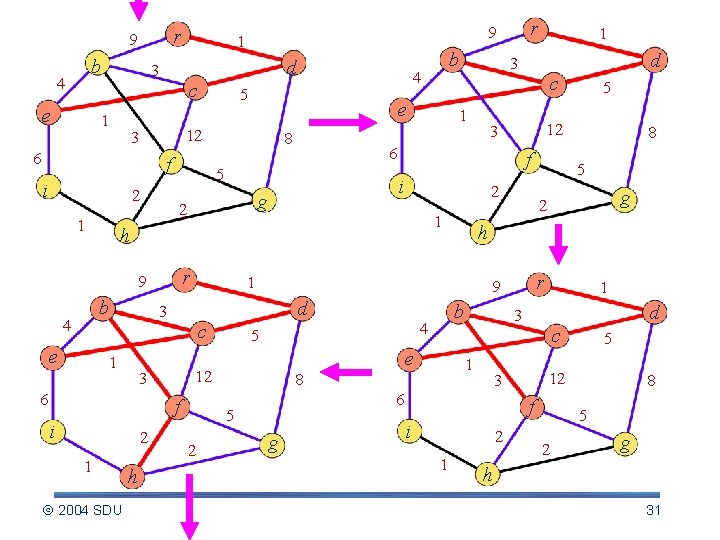
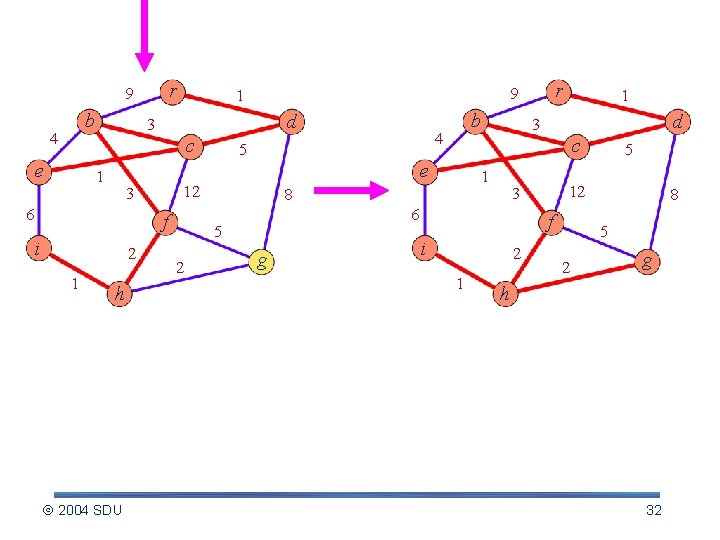
Idea of the Prim 1. Start from a vertex r, add r to a vertex set U which is initialized to empty. 2. Find the least weight edge (u, v), u U, v VU, add (u, v) to A, and add v to U. - A is the loop invariant. 3. Repeat 2 until A forms a spanning tree or U = V. 2004 SDU 28

Prim’s Algorithm //( (u), u) is added to A u is added to U 2004 SDU 29

r 9 b 4 e 1 3 1 f i 2 1 g r 1 f i 2 1 h 2004 SDU 3 6 2 5 2 g h 2 b 4 5 r e g 1 3 1 2 1 5 12 f i d c 3 6 5 8 f 1 8 5 12 9 12 3 6 1 d c 1 3 i h b e 5 2 9 4 e 8 b 4 5 12 3 6 d c r 9 8 5 2 g h 30

r 9 b 4 e d 3 1 c 6 f i 2 1 2 e f i 2 1 r 1 c 6 f i 2 1 2004 SDU h e 12 3 r 1 d c f i 2 1 5 12 3 6 g g 3 1 8 5 2 b 4 5 5 2 9 d 8 h 1 3 5 12 3 6 g d 3 1 h b 4 8 1 c e 5 9 b 4 5 12 3 ra 9 1 8 5 2 g h 31

r 9 b 4 d 3 c e 4 5 12 3 6 f i 2 1 b h 2004 SDU 2 f i 2 1 5 12 3 6 g d 3 1 8 5 1 c e 1 r 9 1 8 5 2 g h 32

Time Complexity Running time § Using binary min-heap – EXTRACT-MIN: return and delete root of the heap, put the last leaf as the new root, and search down to find its proper position. //O(lg. V), total O(Vlg. V) – key(v) w(u, v): check array p[v] to find v’s position in the heap, then change its key value, and search back to find its proper position in the heap. //O(lg. V), total O(Elg. V) – Total: O(E lg V) § Using Fibonacci heap O(E+Vlg. V) 2004 SDU 33

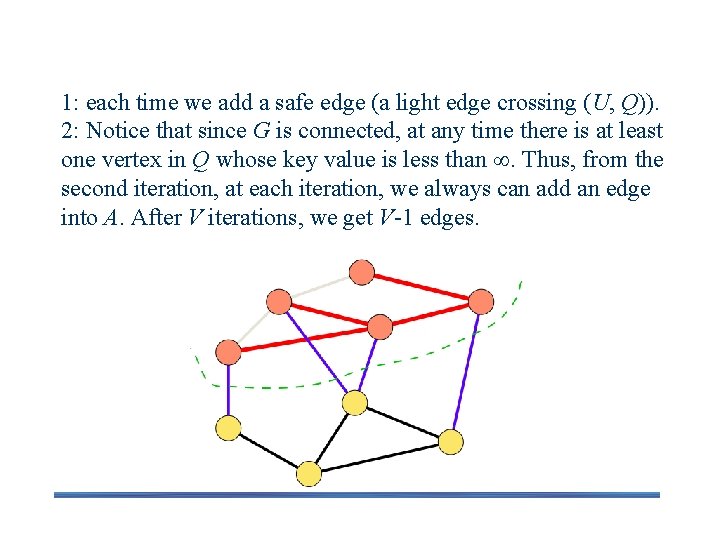
Correctness 1: each time we add a safe edge (a light edge crossing (U, Q)). 2: Notice that since G is connected, at any time there is at least one vertex in Q whose key value is less than . Thus, from the second iteration, at each iteration, we always can add an edge into A. After V iterations, we get V-1 edges.

2004 SDU 35