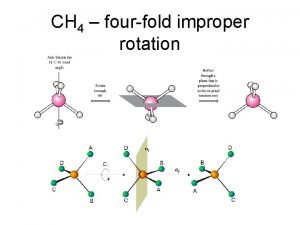
Lecture 3 Principal rotation axis Any C 2

Lecture 3

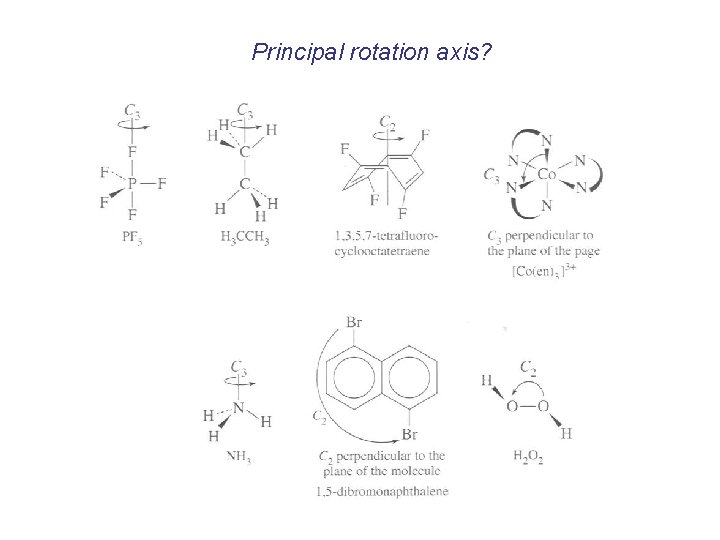
Principal rotation axis?

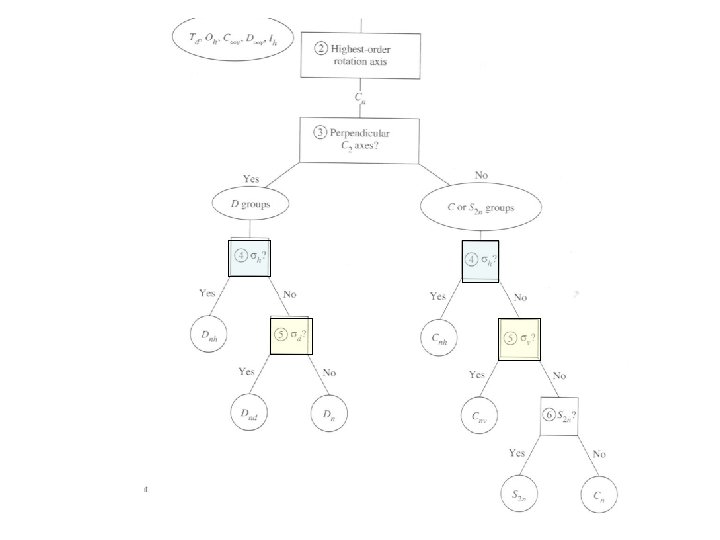
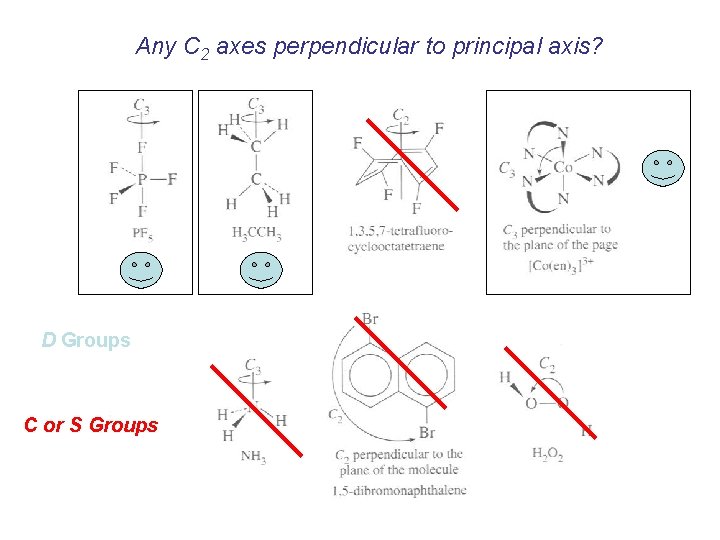
Any C 2 axes perpendicular to principal axis? D Groups C or S Groups

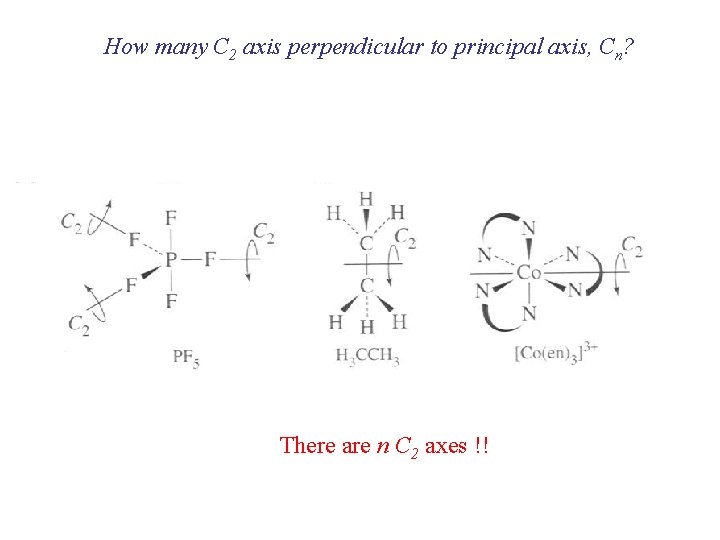
How many C 2 axis perpendicular to principal axis, Cn? There are n C 2 axes !!

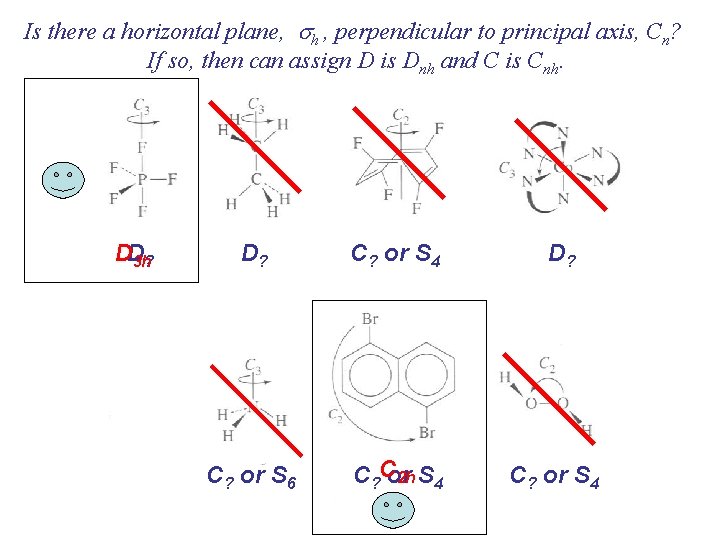
Is there a horizontal plane, sh , perpendicular to principal axis, Cn? If so, then can assign D is Dnh and C is Cnh. DD 3 h? D? C? or S 4 C? or S 6 C? Cor 2 h S 4 D? C? or S 4

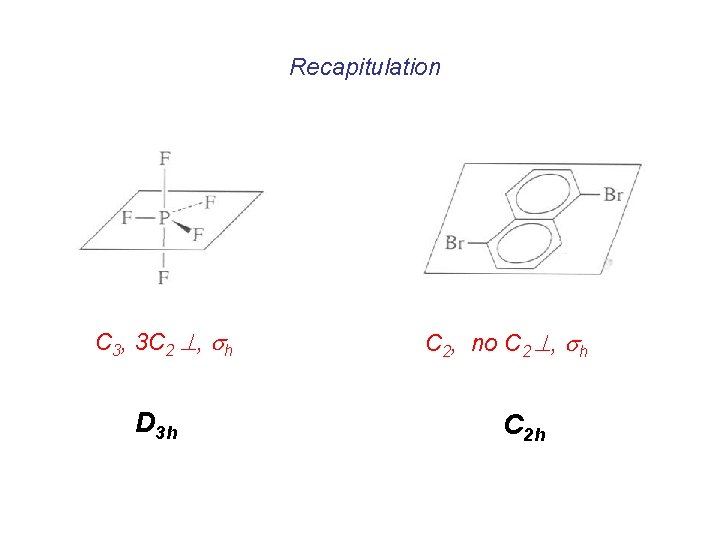
Recapitulation C 3, 3 C 2 , sh D 3 h C 2, no C 2 , sh C 2 h

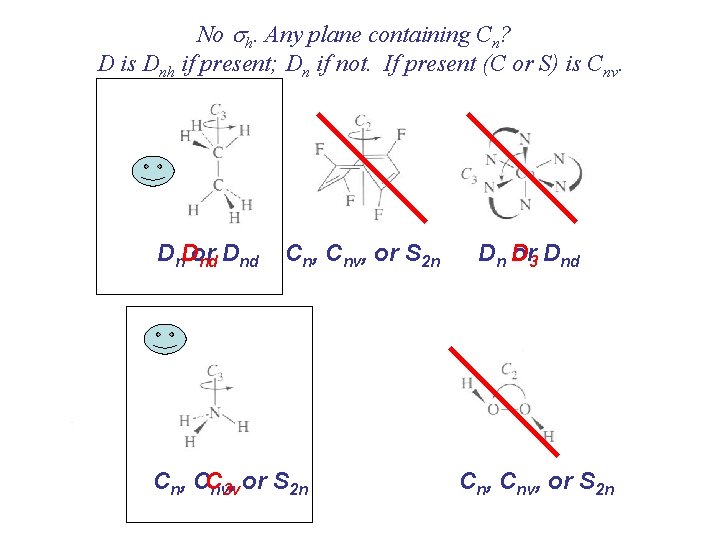
No sh. Any plane containing Cn? D is Dnh if present; Dn if not. If present (C or S) is Cnv. Dn. Dor nd Dnd Cn, Cnv, or S 2 n Cn, CC , or S 2 n nv 3 v Dn D or 3 Dnd Cn, Cnv, or S 2 n

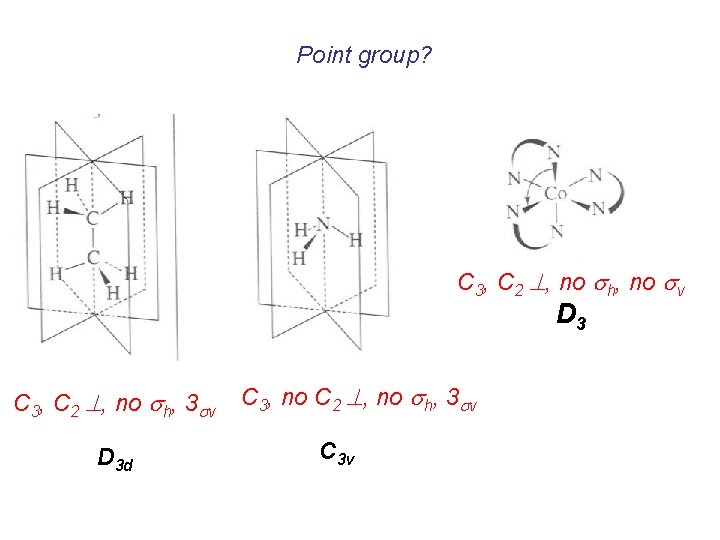
Point group? C 3, C 2 , no sh, no sv D 3 C 3, C 2 , no sh, 3 sv D 3 d C 3, no C 2 , no sh, 3 sv C 3 v

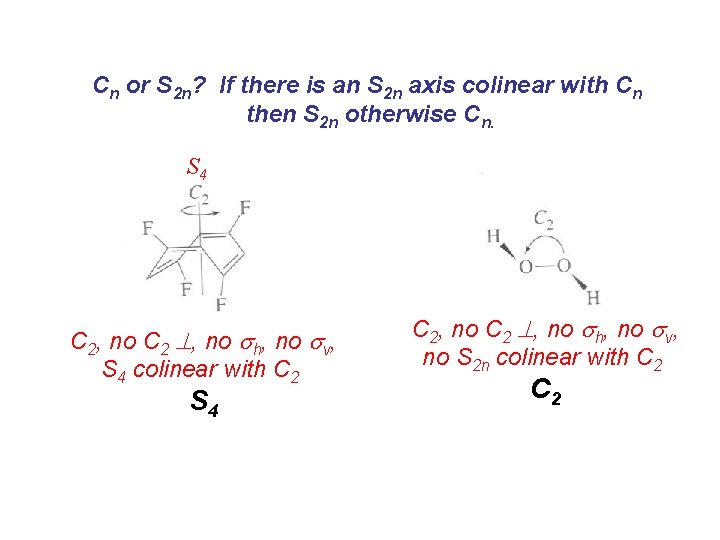
Cn or S 2 n? If there is an S 2 n axis colinear with Cn then S 2 n otherwise Cn. S 4 C 2, no C 2 , no sh, no sv, S 4 colinear with C 2 S 4 C 2, no C 2 , no sh, no sv, no S 2 n colinear with C 2

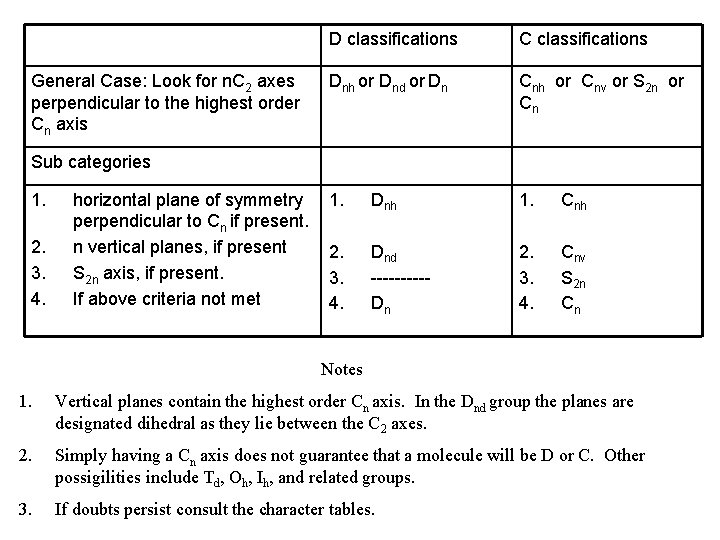
General Case: Look for n. C 2 axes perpendicular to the highest order Cn axis D classifications C classifications Dnh or Dnd or Dn Cnh or Cnv or S 2 n or Cn 1. Dnh 1. Cnh 2. 3. 4. Dnd -----Dn 2. 3. 4. Cnv S 2 n Cn Sub categories 1. 2. 3. 4. horizontal plane of symmetry perpendicular to Cn if present. n vertical planes, if present S 2 n axis, if present. If above criteria not met Notes 1. Vertical planes contain the highest order Cn axis. In the Dnd group the planes are designated dihedral as they lie between the C 2 axes. 2. Simply having a Cn axis does not guarantee that a molecule will be D or C. Other possigilities include Td, Oh, Ih, and related groups. 3. If doubts persist consult the character tables.

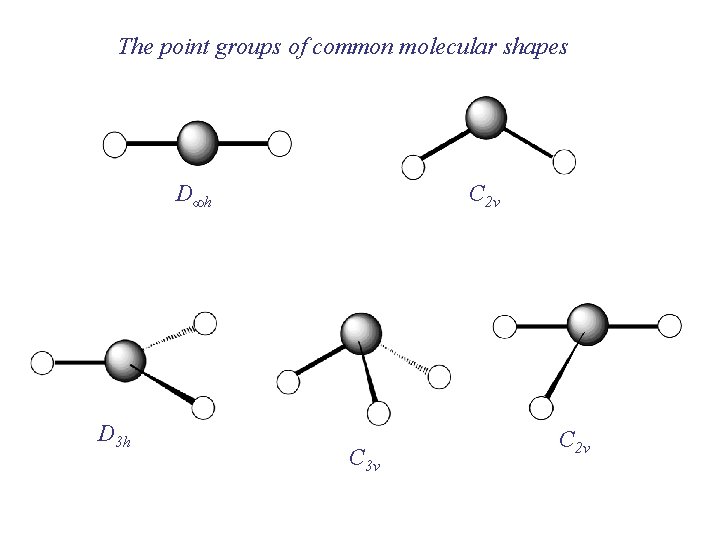
The point groups of common molecular shapes D∞h D 3 h C 2 v C 3 v C 2 v

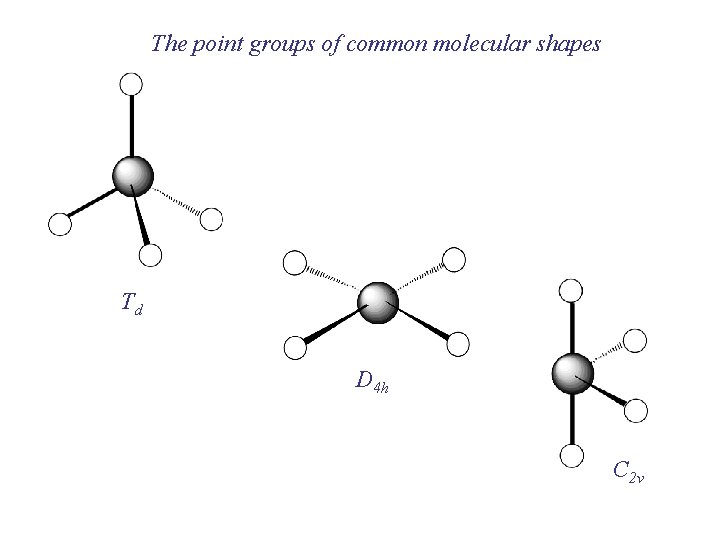
The point groups of common molecular shapes Td D 4 h C 2 v

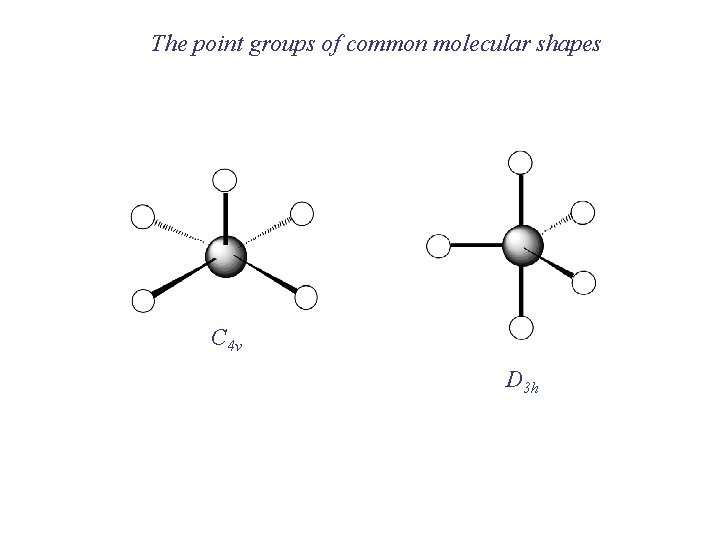
The point groups of common molecular shapes C 4 v D 3 h

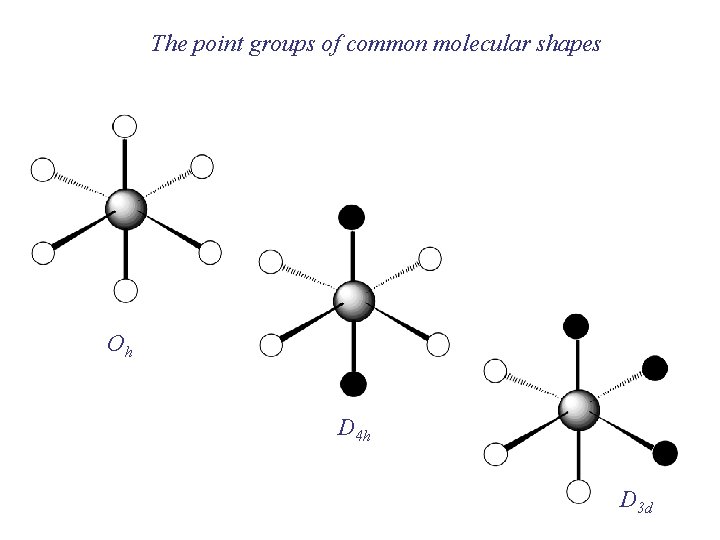
The point groups of common molecular shapes Oh D 4 h D 3 d

Character Tables Group theory makes use of the properties of matrices Each symmetry operation may be expressed as a transformation matrix: [New coordinates] = [transformation matrix][old coordinates] Example: in Cartesian coordinate system, reflection in x = 0 plane • Changes the value of x to –x, multiplies it by -1 • Leaves y unchanged • Leaves z unchanged = Results of transformation. Transformation Original matrix coordinates

Matrix multiplication = V’ M V To get an element of the product vector a row in the operation square matrix is multiplied by the original vector matrix. For example V’ 2 = y’ = M 2, 1 * V 1 + M 2, 2 * V 2 + M 2, 3 * V 3 y’ = 0 * x + 1 * y + 0 * z = y

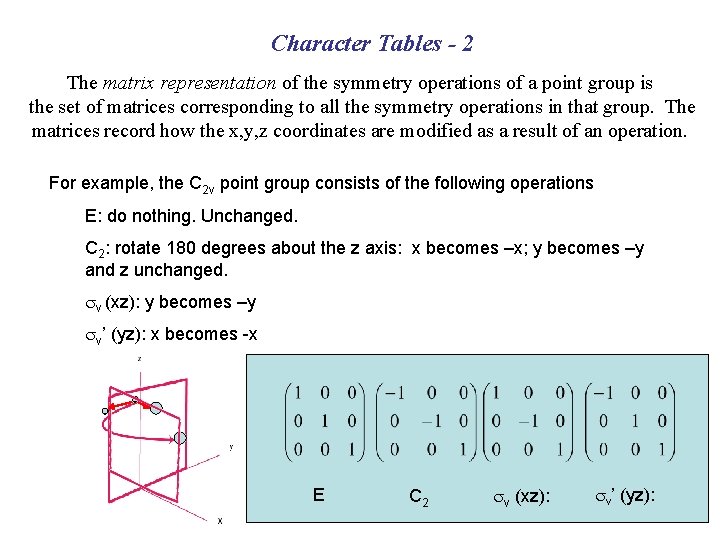
Character Tables - 2 The matrix representation of the symmetry operations of a point group is the set of matrices corresponding to all the symmetry operations in that group. The matrices record how the x, y, z coordinates are modified as a result of an operation. For example, the C 2 v point group consists of the following operations E: do nothing. Unchanged. C 2: rotate 180 degrees about the z axis: x becomes –x; y becomes –y and z unchanged. sv (xz): y becomes –y sv’ (yz): x becomes -x E C 2 sv (xz): sv’ (yz):

Operations Applied to Functions - 1 Consider f(x) = x 2 sv’ (f(x)) = sv(x 2) = (-x)2 = x 2 = f(x) or sv’ (f(x)) = 1 * f(x) is an eigenfunction of this reflection operator with an eigenvalue of +1. This is called a symmetric eigenfunction. Similarly f(x) = x 3 sv’ (f(x)) = -1 * f(x) is an eigenfunction of this reflection operator with an eigenvalue of -1. This is called a antisymmetric eigenfunction.

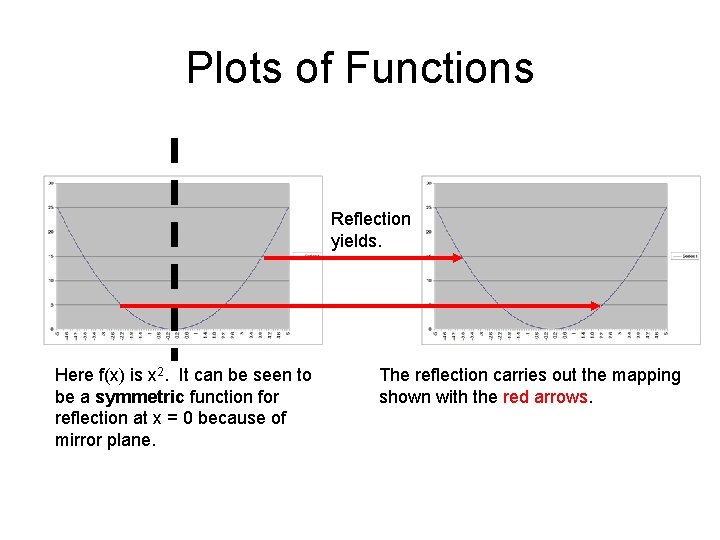
Plots of Functions Reflection yields. Here f(x) is x 2. It can be seen to be a symmetric function for reflection at x = 0 because of mirror plane. The reflection carries out the mapping shown with the red arrows.

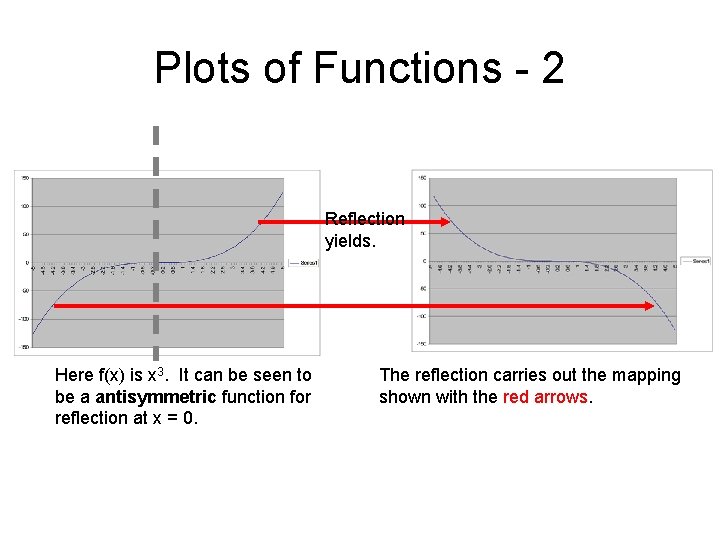
Plots of Functions - 2 Reflection yields. Here f(x) is x 3. It can be seen to be a antisymmetric function for reflection at x = 0. The reflection carries out the mapping shown with the red arrows.

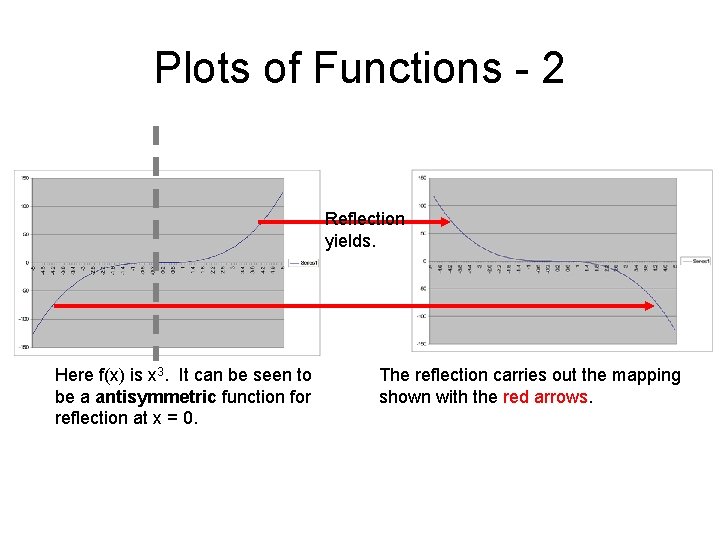
Plots of Functions - 2 Reflection yields. Here f(x) is x 3. It can be seen to be a antisymmetric function for reflection at x = 0. The reflection carries out the mapping shown with the red arrows.

Operations Applied to Functions - 2 Now consider f(x) = (x-2)2 = x 2 – 4 x + 4 sv’ (f(x)) = sv(x-2)2 = (-x-2)2 = x 2 + 4 x + 4 f(x) = (x-2)2 is not an eigenfunction of this reflection operator because it does not return a constant times f(x). Reflection yields this function, not an eigenfunc tion. Neither symmetric nor antisymmetric for reflection thru x = 0.

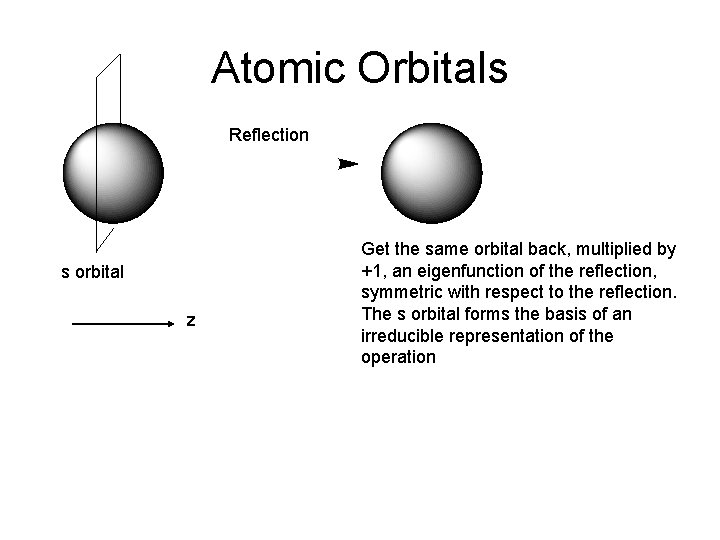
Atomic Orbitals Reflection s orbital z Get the same orbital back, multiplied by +1, an eigenfunction of the reflection, symmetric with respect to the reflection. The s orbital forms the basis of an irreducible representation of the operation

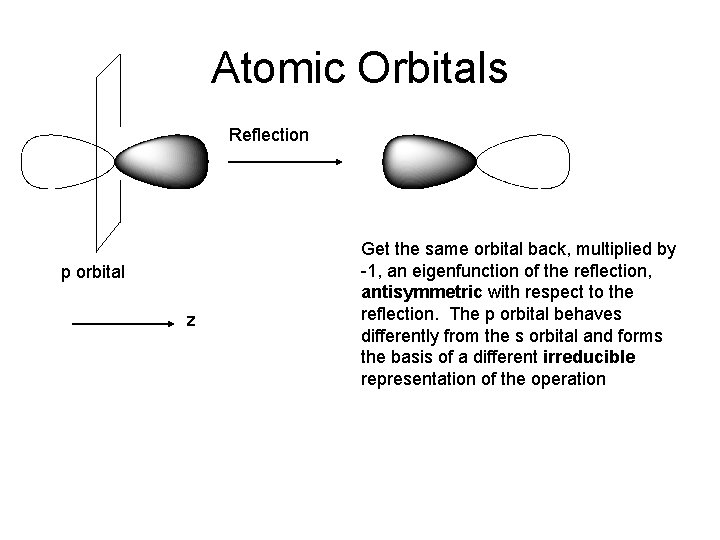
Atomic Orbitals Reflection p orbital z Get the same orbital back, multiplied by -1, an eigenfunction of the reflection, antisymmetric with respect to the reflection. The p orbital behaves differently from the s orbital and forms the basis of a different irreducible representation of the operation

Different ways that objects can behave for a group consisting of E and the reflection plane. Cs E sh A’ A” 1 1 1 x, y, Rz x 2, y 2, z 2, xy -1 z, Rx, Ry yz, xz s orbital is spherical behaves as x 2 + y 2 + z 2. s orbital is A’ pz orbital has a multiplicative factor of z times a spherical factor. Behaves as A”.

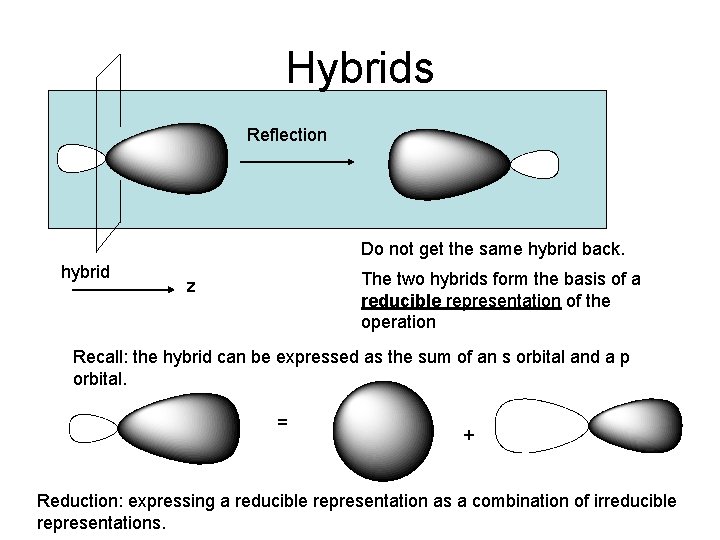
Hybrids Reflection Do not get the same hybrid back. hybrid The two hybrids form the basis of a reducible representation of the operation z Recall: the hybrid can be expressed as the sum of an s orbital and a p orbital. = + Reduction: expressing a reducible representation as a combination of irreducible representations.

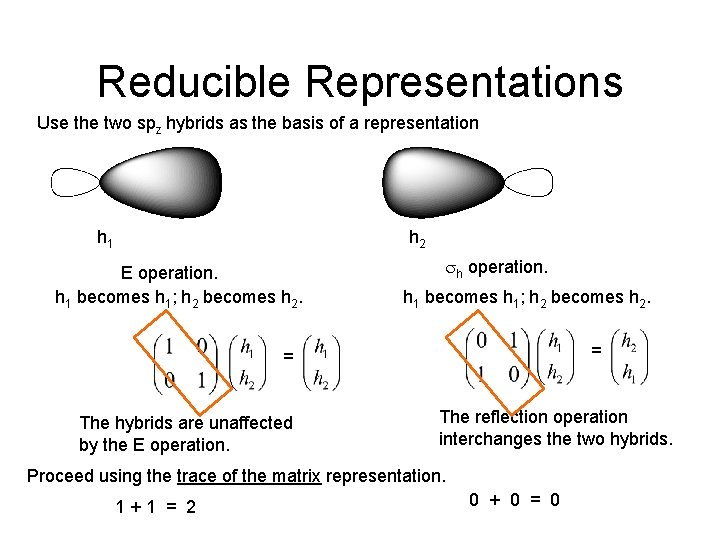
Reducible Representations Use the two spz hybrids as the basis of a representation h 1 h 2 E operation. h 1 becomes h 1; h 2 becomes h 2. sh operation. h 1 becomes h 1; h 2 becomes h 2. = = The hybrids are unaffected by the E operation. The reflection operation interchanges the two hybrids. Proceed using the trace of the matrix representation. 1+1 = 2 0 + 0 = 0

Representations Cs E sh A’ A” 1 1 1 x, y, Rz x 2, y 2, z 2, xy -1 z, Rx, Ry yz, xz The representation derived from the two hybrids can be attached to the table. G 2 0 (h 1, h 2) Note that G = A’ + A”

Character Tables - 3 Irreducible representations are not linear combinations of other representation (Reducible representations are) # of irreducible representations = # of classes of symmetry operations Instead of the matrices, the characters are used (traces of matrices) A character Table is the complete set of irreducible representations of a point group

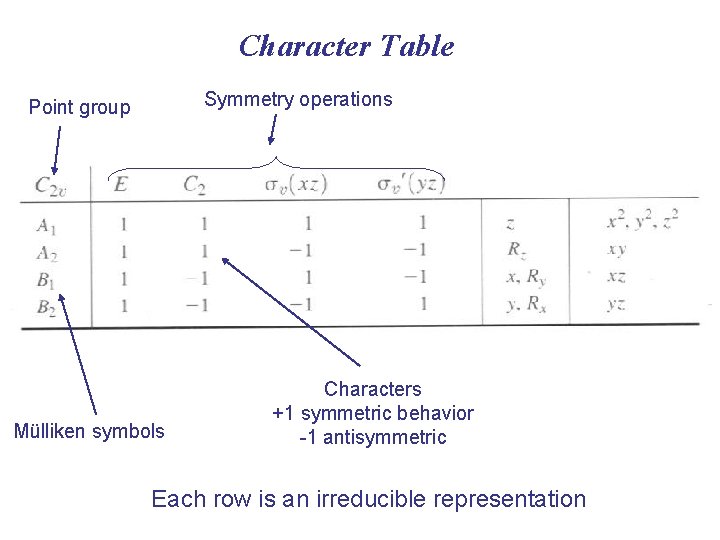
Character Table Symmetry operations Point group Mülliken symbols Characters +1 symmetric behavior -1 antisymmetric Each row is an irreducible representation

Classes of operations dxy, dxz, dyz, as xy, xz, yz dx 2 - y 2 behaves as x 2 – y 2 dz 2 behaves as 2 z 2 - (x 2 + y 2) px, py, pz behave as x, y, z s behaves as x 2 + y 2 + z 2 x, y, z Symmetry of translations (p orbitals) Rx, Ry, Rz: rotations