CH 4 fourfold improper rotation Special Features of

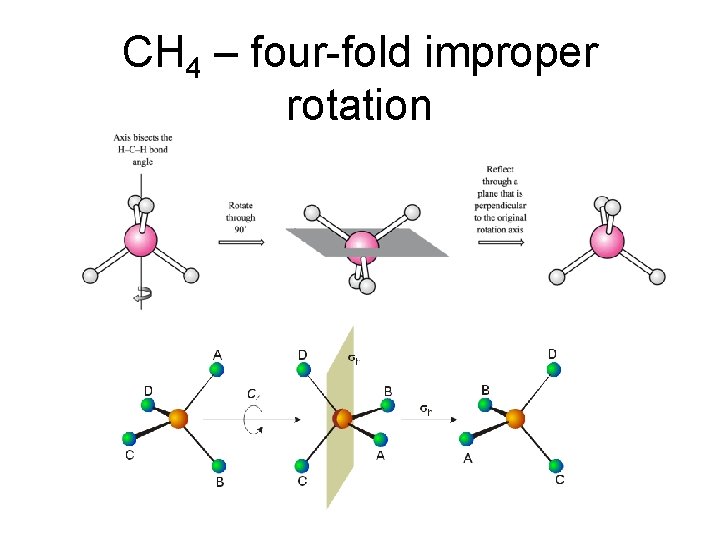
CH 4 – four-fold improper rotation

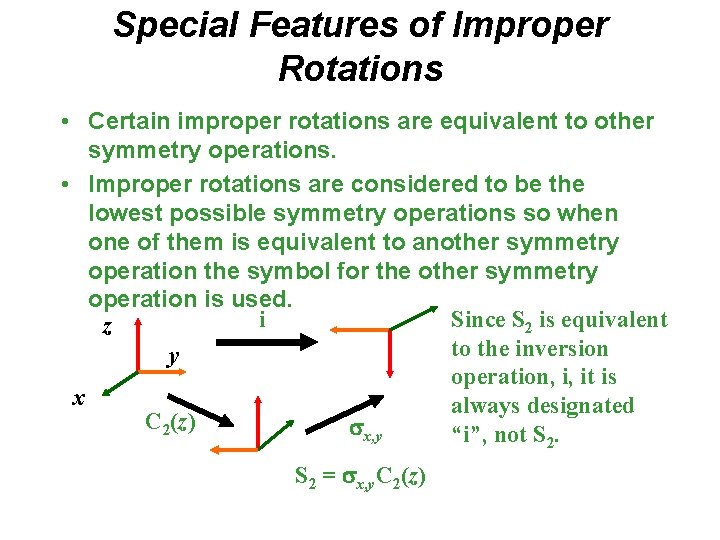
Special Features of Improper Rotations • Certain improper rotations are equivalent to other symmetry operations. • Improper rotations are considered to be the lowest possible symmetry operations so when one of them is equivalent to another symmetry operation the symbol for the other symmetry operation is used. i Since S 2 is equivalent z to the inversion y operation, i, it is x always designated C 2(z) x, y “i”, not S 2 = x, y. C 2(z)

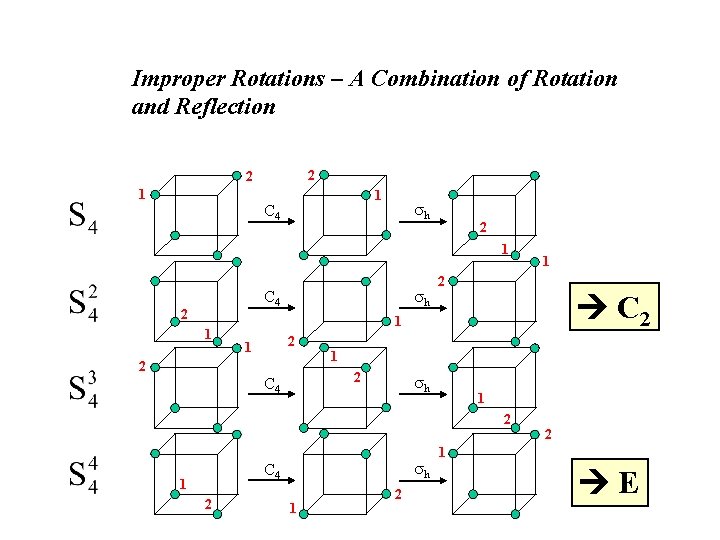
Improper Rotations – A Combination of Rotation and Reflection 2 2 1 1 C 4 h 2 1 h C 4 2 1 1 2 C 2 1 2 1 2 C 4 h 1 2 2 h C 4 1 2 1 E

• Consider the operation Snm for even values of m. – The reflection operation in S is always done an even number of times so Snm = Cnm E = Cnm when m is even. • Consider the operation Snn for odd values of n. – In this specific case where n = m, the rotation operation has been carried through an angle of 2. – Since n is odd, the reflection operation is carried out an odd number of times so n = . – The result is that in the specific case where n is odd, Snn = . • Consider Snm generally when n is odd. – When n is odd, Snn = and Snn+1 = Cn. – When n is even, Snn = E and Snn+1 = Sn and cannot be reduced except for S 2 which is the same as the inversion. – We conclude that when n is odd, the existence of a Sn axis requires the existence of both a Cn axis and a plane.

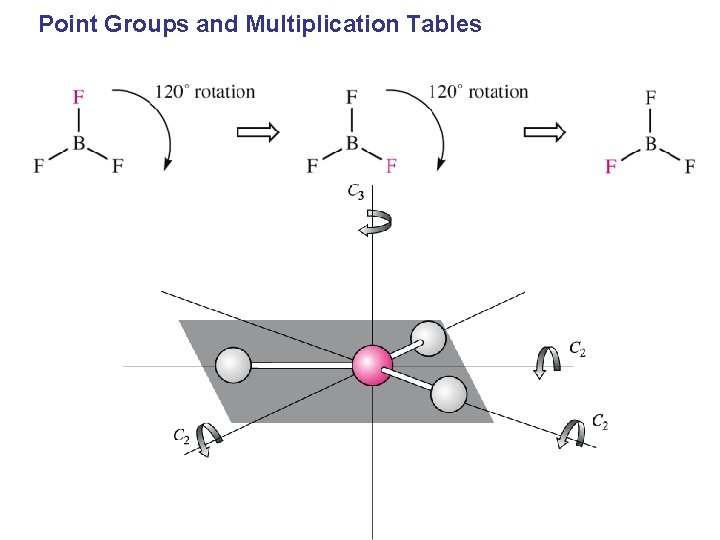
Point Groups and Multiplication Tables

Point groups • So called because all the symmetry elements pass through one common point • It is useful to be able to classify the molecular point group so that we can easily identify all the symmetry elements • Symmetry classification can be used to discuss molecular properties. • We can use symmetry transformations of orbitals to decide which atomic orbitals contribute to the formation of molecular orbitals, and select linear combinations of atomic orbitals that match the symmetry of the molecule.

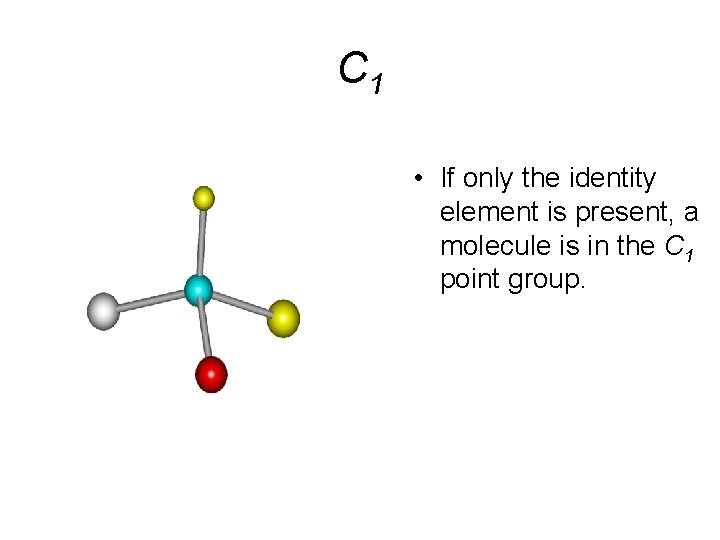
C 1 • If only the identity element is present, a molecule is in the C 1 point group.

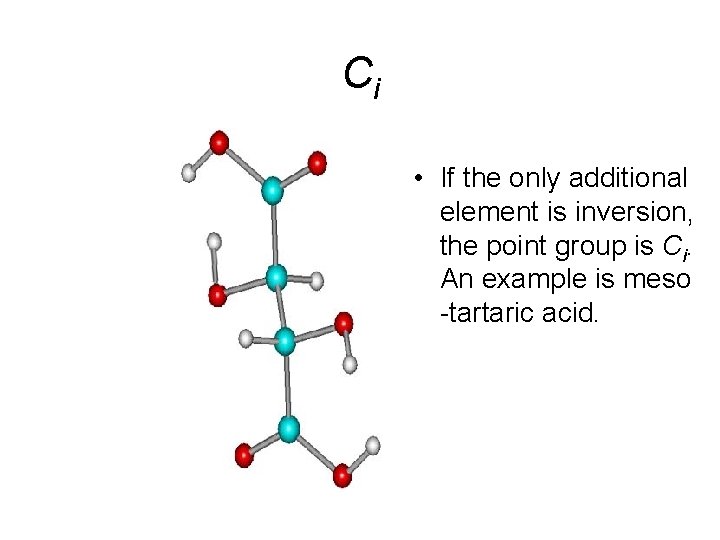
Ci • If the only additional element is inversion, the point group is Ci. An example is meso -tartaric acid.

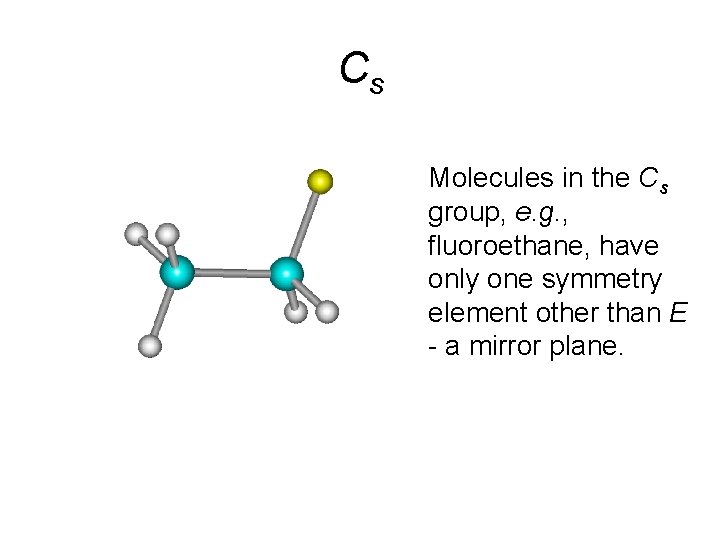
Cs • Molecules in the Cs group, e. g. , fluoroethane, have only one symmetry element other than E - a mirror plane.

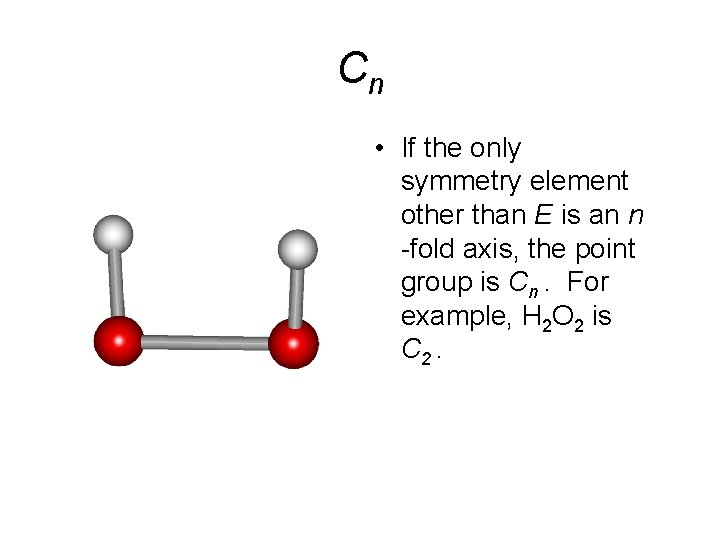
Cn • If the only symmetry element other than E is an n -fold axis, the point group is Cn. For example, H 2 O 2 is C 2.

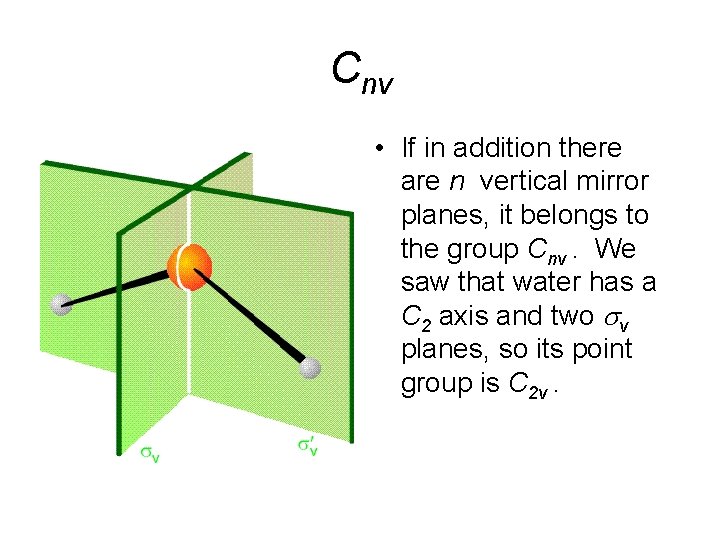
Cnv • If in addition there are n vertical mirror planes, it belongs to the group Cnv. We saw that water has a C 2 axis and two sv planes, so its point group is C 2 v.

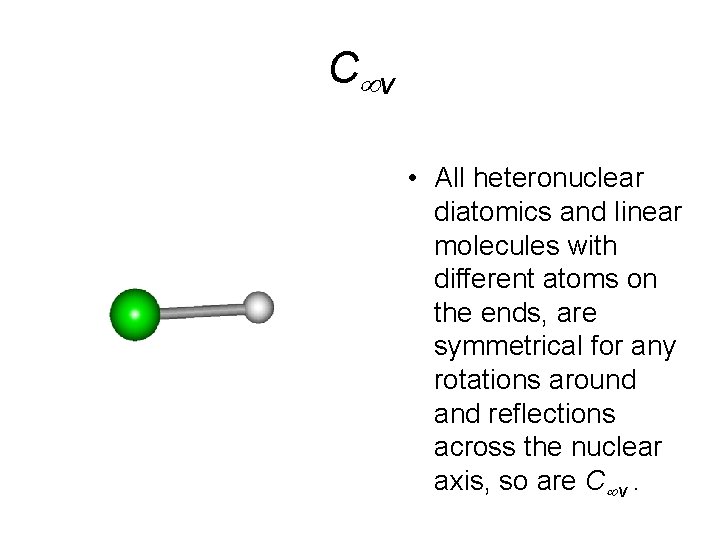
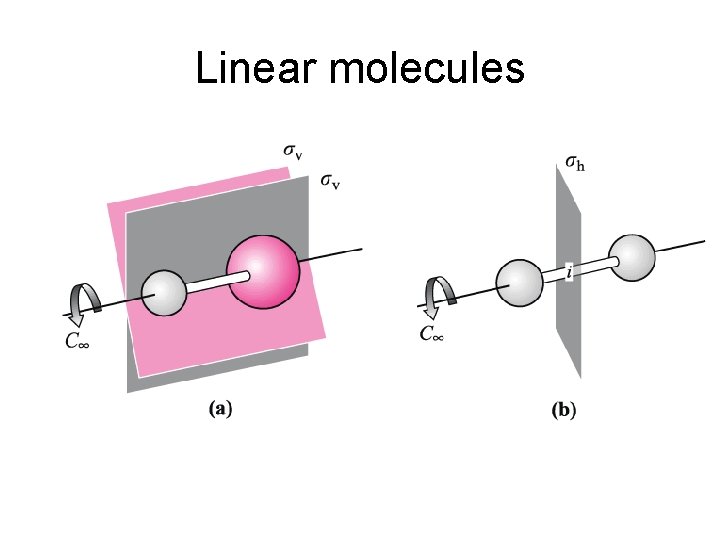
C v • All heteronuclear diatomics and linear molecules with different atoms on the ends, are symmetrical for any rotations around and reflections across the nuclear axis, so are C v.

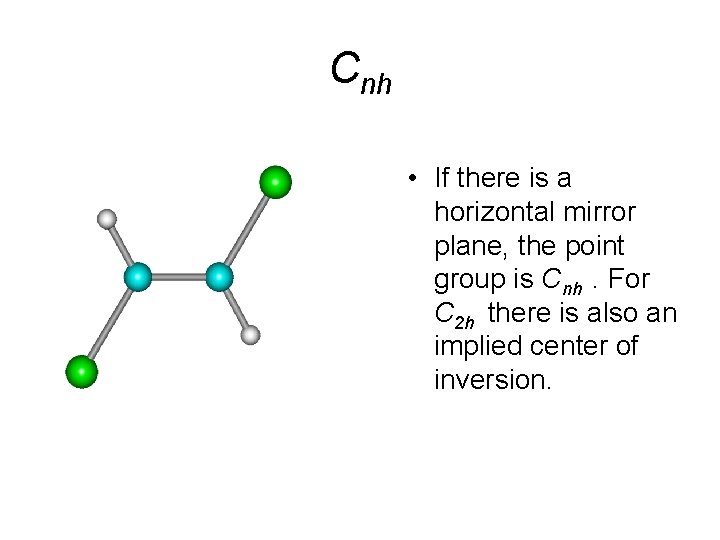
Cnh • If there is a horizontal mirror plane, the point group is Cnh. For C 2 h there is also an implied center of inversion.

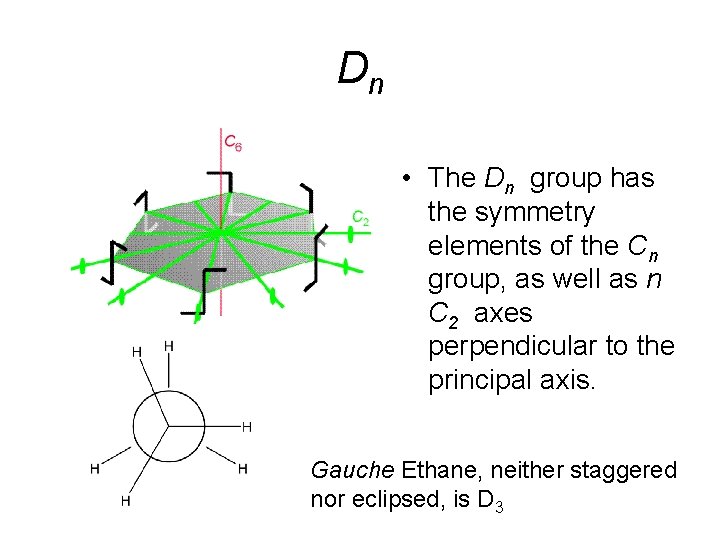
Dn • The Dn group has the symmetry elements of the Cn group, as well as n C 2 axes perpendicular to the principal axis. Gauche Ethane, neither staggered nor eclipsed, is D 3

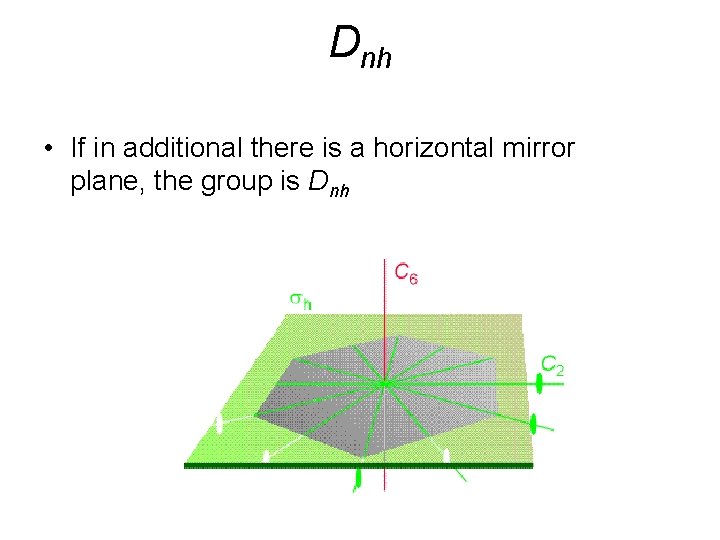
Dnh • If in additional there is a horizontal mirror plane, the group is Dnh

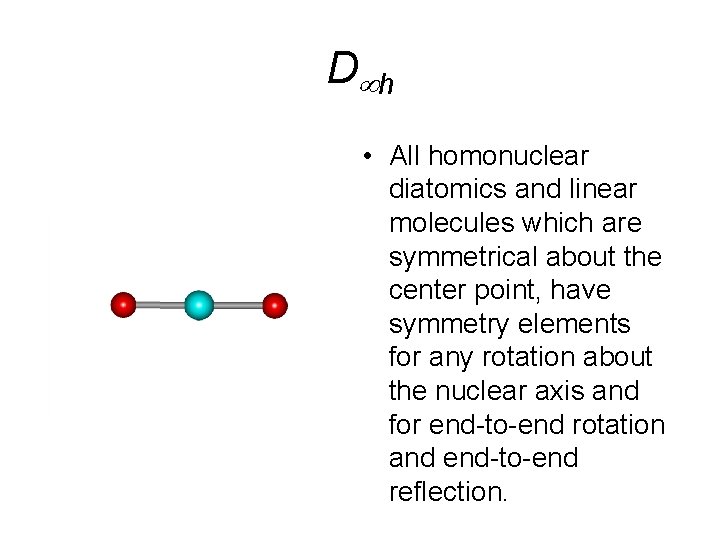
D h • All homonuclear diatomics and linear molecules which are symmetrical about the center point, have symmetry elements for any rotation about the nuclear axis and for end-to-end rotation and end-to-end reflection.

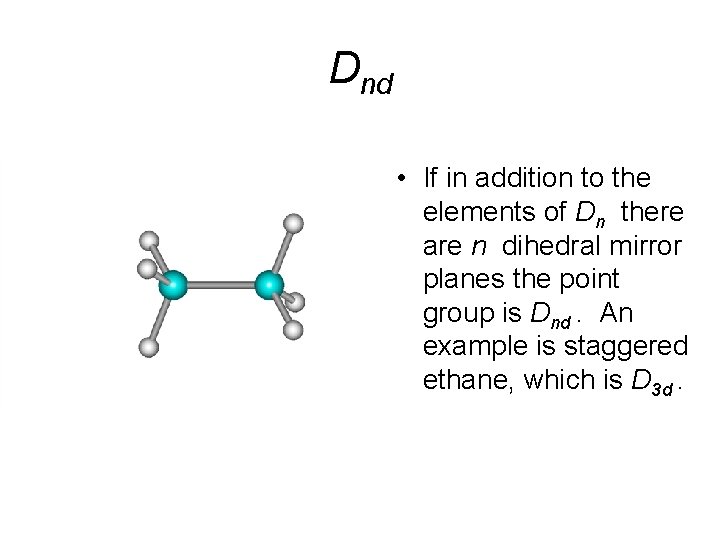
Dnd • If in addition to the elements of Dn there are n dihedral mirror planes the point group is Dnd. An example is staggered ethane, which is D 3 d.

Sn • Molecules which do not fit one of the above classifications, but which possess one Sn axis, belong to the Sn group. • n is a multiple of two, but S 2 is equivalent to Ci , and the latter designation takes precedence. • Members of the Sn group also have a Cn/2 axis; e. g. , an S 4 molecule will have a C 2 axis.

The cubic groups • So far we have seen molecules with one principal axis (if any). • Some highly symmetrical molecules have more than one principal axis, and most of these belong to the cubic groups.

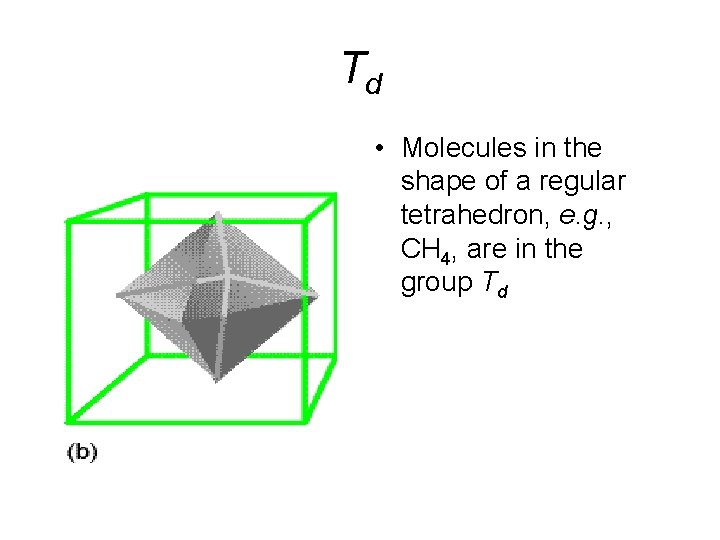
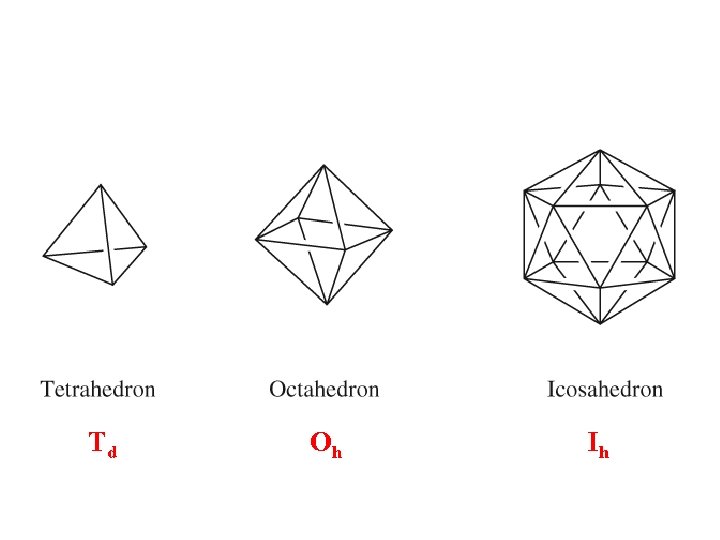
Td • Molecules in the shape of a regular tetrahedron, e. g. , CH 4, are in the group Td

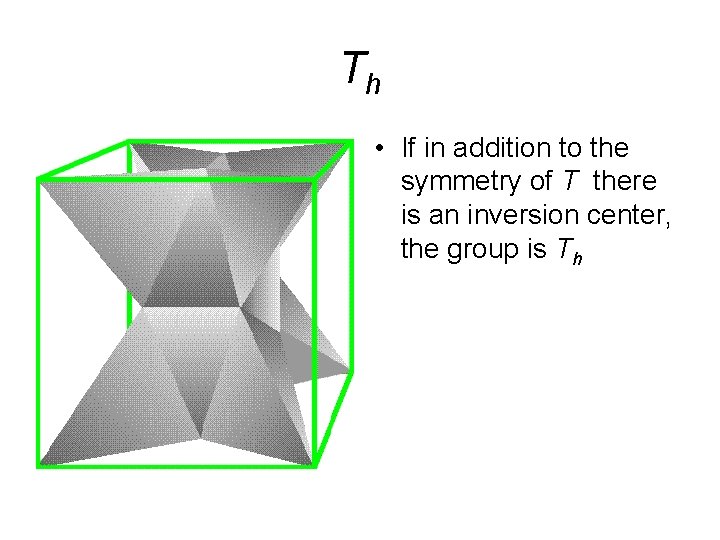
Th • If in addition to the symmetry of T there is an inversion center, the group is Th

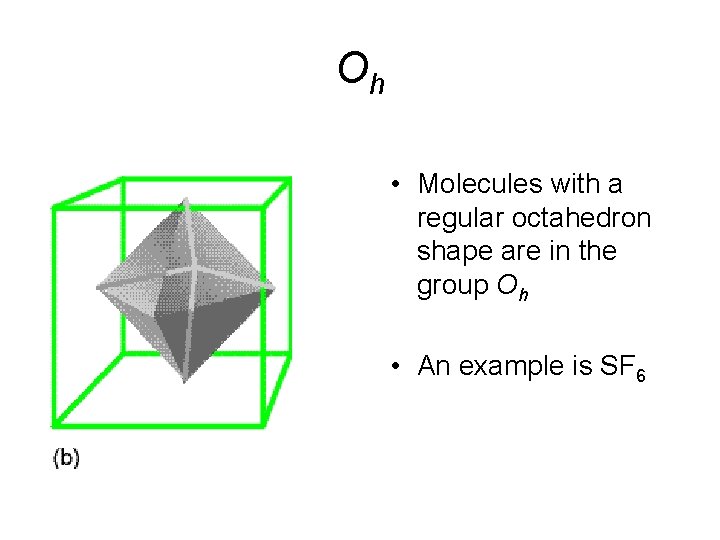
Oh • Molecules with a regular octahedron shape are in the group Oh • An example is SF 6

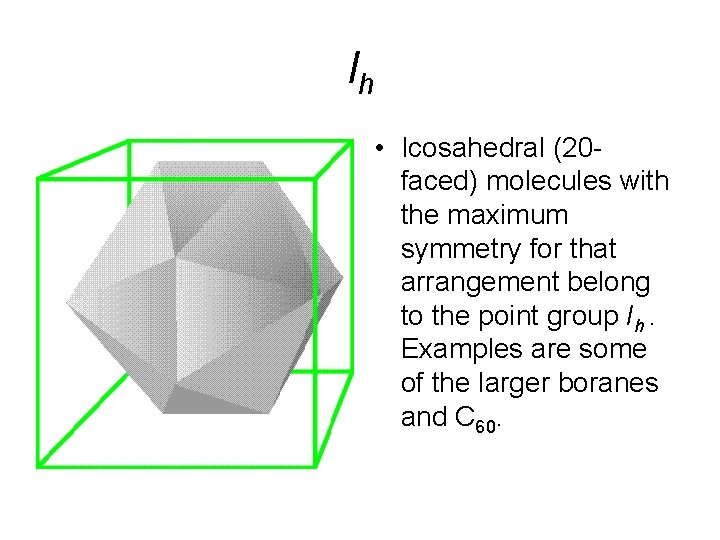
Ih • Icosahedral (20 faced) molecules with the maximum symmetry for that arrangement belong to the point group Ih. Examples are some of the larger boranes and C 60.

Td Oh Ih

Linear molecules

R 3 • An atom or a sphere has an infinite number of rotation axes in three dimensions and for all possible values of n. In these cases the point group is R 3

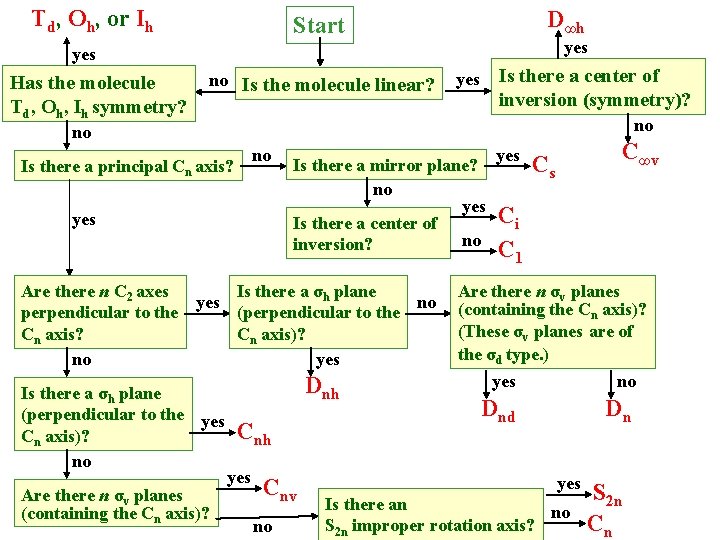
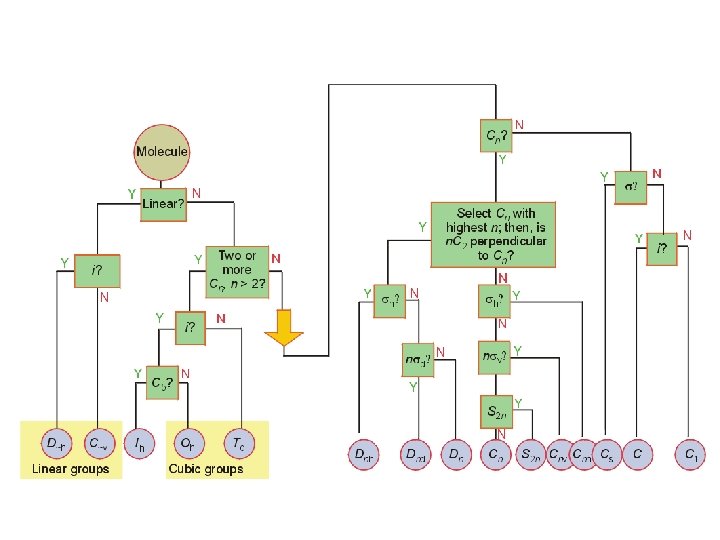
Td, Oh, or Ih D∞h Start yes Has the molecule Td, Oh, Ih symmetry? no Is the molecule linear? Is there a center of inversion (symmetry)? yes no no no Is there a principal Cn axis? yes Is there a mirror plane? no yes Is there a center of no inversion? Are there n C 2 axes Is there a σh plane yes no perpendicular to the (perpendicular to the Cn axis? Cn axis)? no yes Is there a σh plane (perpendicular to the yes Cn axis)? no Are there n σv planes (containing the Cn axis)? Dnh Cnh yes Cnv no yes C∞v Cs Ci C 1 Are there n σv planes (containing the Cn axis)? (These σv planes are of the σd type. ) yes no Dnd Dn yes Is there an no S 2 n improper rotation axis? S 2 n Cn