Last Time Introduction to parametric curves Hermite curves

Last Time • • Introduction to parametric curves Hermite curves Bezier curves Continuity 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Today • Geometric continuity • Parametric surfaces – General Tensor product surfaces – Bezier surfaces • BSplines • Homework 7 available, due Thursday May 6 in class 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Continuity • When two curves are joined, we typically want some degree of continuity across the boundary (the knot) – C 0, “C-zero”, point-wise continuous, curves share the same point where they join – C 1, “C-one”, continuous derivatives, curves share the same parametric derivatives where they join – C 2, “C-two”, continuous second derivatives, curves share the same parametric second derivatives where they join – Higher orders possible 4/27/04 © University of Wisconsin, CS 559 Spring 2004

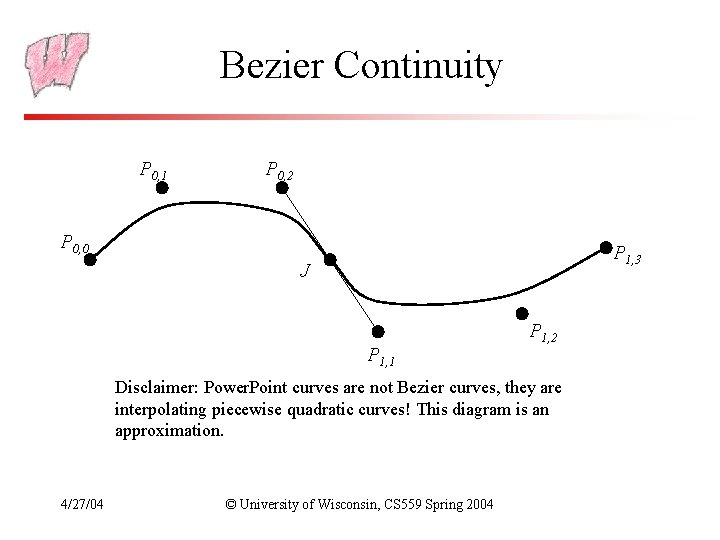
Bezier Continuity P 0, 1 P 0, 2 P 0, 0 P 1, 3 J P 1, 1 P 1, 2 Disclaimer: Power. Point curves are not Bezier curves, they are interpolating piecewise quadratic curves! This diagram is an approximation. 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Sketch of Proof for C 1 Bezier curve equation: Parametric derivative: Evaluated at endpoint of curve (note proves tangent property): 4/27/04 © University of Wisconsin, CS 559 Spring 2004

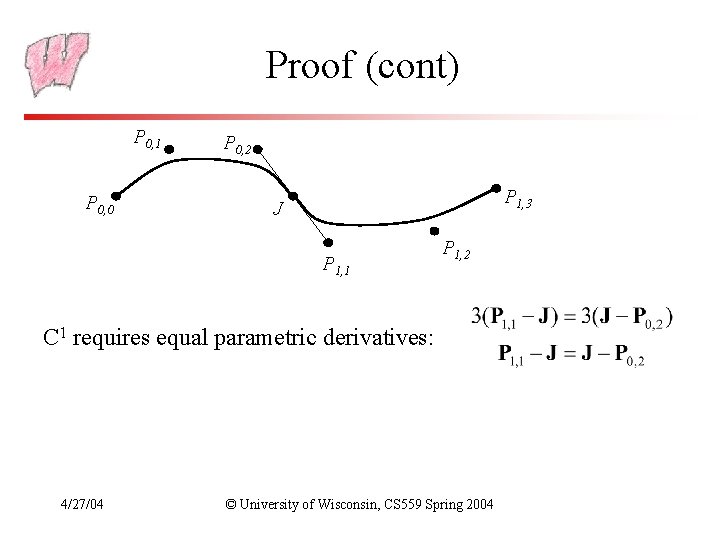
Proof (cont) P 0, 1 P 0, 0 P 0, 2 P 1, 3 J P 1, 1 P 1, 2 C 1 requires equal parametric derivatives: 4/27/04 © University of Wisconsin, CS 559 Spring 2004

DOF and Locality • The number of degrees of freedom (DOF) can be thought of as the number of things a user gets to specify – If we have n piecewise Bezier curves joined with C 0 continuity, how many DOF does the user have? – If we have n piecewise Bezier curves joined with C 1 continuity, how many DOF does the user have? • Locality refers to the number of curve segments affected by a change in a control point – Local change affects fewer segments – How many segments of a piecewise cubic Bezier curve are affected by each control point if the curve has C 1 continuity? – What about C 2? 4/27/04 © University of Wisconsin, CS 559 Spring 2004

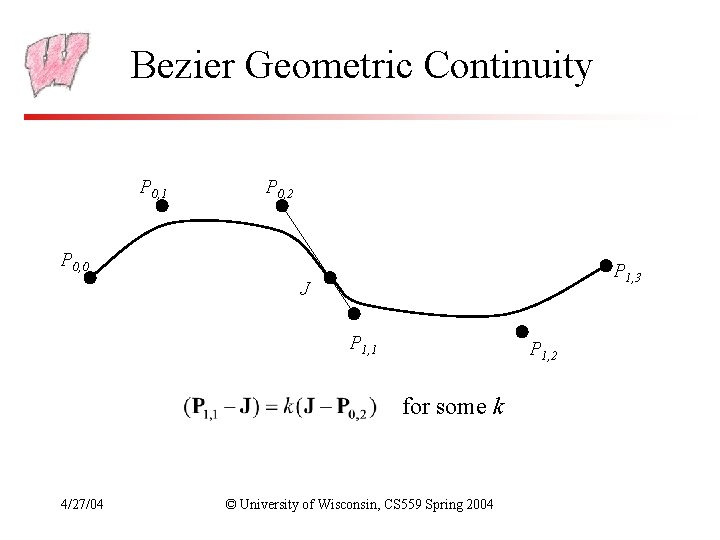
Geometric Continuity • Derivative continuity is important for animation – If an object moves along the curve with constant parametric speed, there should be no sudden jump at the knots • For other applications, tangent continuity might be enough – – Requires that the tangents point in the same direction Referred to as G 1 geometric continuity Curves could be made C 1 with a re-parameterization: u=f(t) The geometric version of C 2 is G 2, based on curves having the same radius of curvature across the knot • What is the tangent continuity constraint for a Bezier curve? 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Bezier Geometric Continuity P 0, 1 P 0, 2 P 0, 0 P 1, 3 J P 1, 1 P 1, 2 for some k 4/27/04 © University of Wisconsin, CS 559 Spring 2004

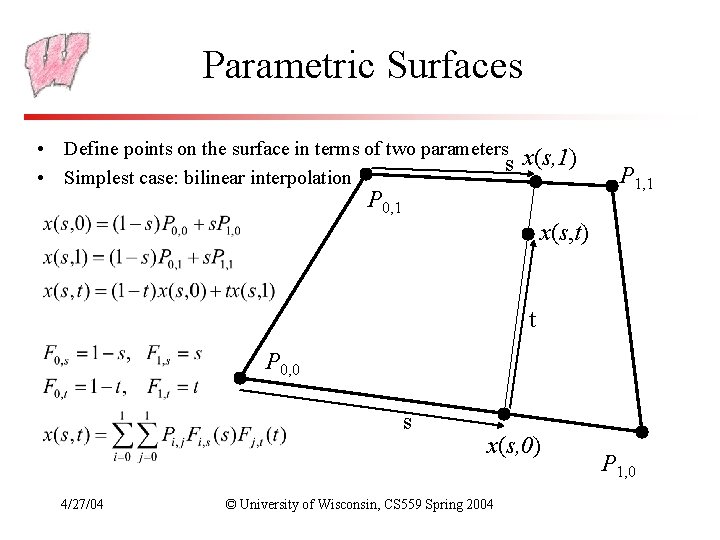
Parametric Surfaces • Define points on the surface in terms of two parameters x(s, 1) s • Simplest case: bilinear interpolation P 0, 1 P 1, 1 x(s, t) t P 0, 0 s 4/27/04 x(s, 0) © University of Wisconsin, CS 559 Spring 2004 P 1, 0

Tensor Product Surface Patches • Defined over a rectangular domain – Valid parameter values come from within a rectangular region in parameter space: 0 s<1, 0 t<1 • Use a rectangular grid of control points to specify the surface – 4 points in the bi-linear case on the previous slide, more in other cases • Surface takes the form: – For some functions Fi, s and Fj, t 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Bezier Patches • As with Bezier curves, Bin(s) and Bjm(t) are the Bernstein polynomials of degree n and m respectively • Most frequently, use n=m=3: cubic Bezier patch – Need 4 x 4=16 control points, Pi, j 4/27/04 © University of Wisconsin, CS 559 Spring 2004

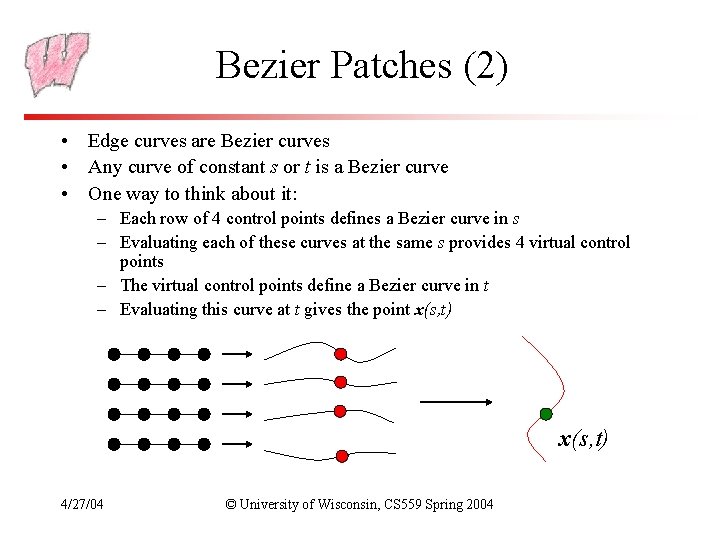
Bezier Patches (2) • Edge curves are Bezier curves • Any curve of constant s or t is a Bezier curve • One way to think about it: – Each row of 4 control points defines a Bezier curve in s – Evaluating each of these curves at the same s provides 4 virtual control points – The virtual control points define a Bezier curve in t – Evaluating this curve at t gives the point x(s, t) 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Properties of Bezier Patches • Which vertices, if any, does the patch interpolate? Why? • What can you say about the tangent plane at each corner? Why? • Does the patch lie within the convex hull of its control vertices? 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Properties of Bezier Patches • The patch interpolates its corner points – Comes from the interpolation property of the underlying curves • The tangent plane at each corner interpolates the corner vertex and the two neighboring edge vertices – The tangent plane is the plane that is perpendicular to the normal vector at a point – The tangent plane property derives from the curve tangent properties and the way to compute normal vectors • The patch lies within the convex hull of its control vertices – The basis functions sum to one and are positive everywhere 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Bezier Patch Matrix Form • Note that the 3 matrices stay the same if the control points do not change – The middle product can be pre-computed, leaving only: 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Bezier Patch Meshes • A patch mesh is just many patches joined together along their edges – Patches meet along complete edges – Each patch must be a quadrilateral OK OK 4/27/04 Not OK © University of Wisconsin, CS 559 Spring 2004 Not OK

Bezier Mesh Continuity • Just like curves, the control points must satisfy constraints to ensure parametric continuity – How do we ensure C 0 continuity along an edge? – How do we ensure C 1 continuity along an edge? – How do we ensure C 2 continuity along an edge? • For geometric continuity, constraints are less rigid • What can you say about the vertices around a corner if there must be C 1 continuity at the corner point? 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Bezier Mesh Continuity • Just like curves, the control points must satisfy rigid constraints to ensure parametric continuity – C 0 continuity along an edge? Share control points at the edge – C 1 continuity along an edge? Control points across edge are collinear and equally spaced – C 2 continuity along an edge? Constraints extent to points farther from the edge • For geometric continuity, constraints are less rigid – Still collinear for G 1, but can be anywhere along the line • What can you say about the vertices around a corner if there must be C 1 continuity at the corner point? – They are co-planar (not the interior points, just corner and edge) 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Rendering Bezier Patches • Option 1: Evaluate at fixed set of parameter values and join up with triangles – – Can’t use quadrilaterals because points may not be co-planar Ideal situation for triangle strips Advantage: Simple, and Open. GL has commands to do it for you Disadvantage: No easy way to control quality of appearance • Option 2: Subdivision – Allows control of error in the triangle approximation – Extend 1 D curve subdivision to do surfaces – Similar to other subdivision schemes we’ve seen 4/27/04 © University of Wisconsin, CS 559 Spring 2004

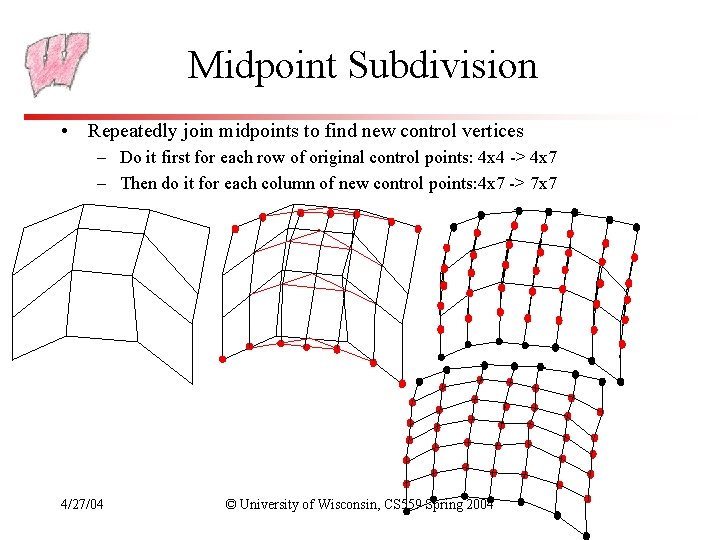
Midpoint Subdivision • Repeatedly join midpoints to find new control vertices – Do it first for each row of original control points: 4 x 4 -> 4 x 7 – Then do it for each column of new control points: 4 x 7 -> 7 x 7 4/27/04 © University of Wisconsin, CS 559 Spring 2004

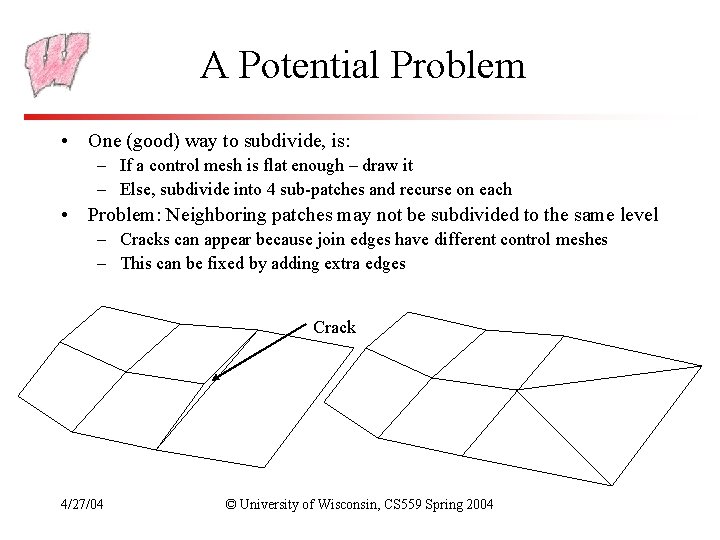
A Potential Problem • One (good) way to subdivide, is: – If a control mesh is flat enough – draw it – Else, subdivide into 4 sub-patches and recurse on each • Problem: Neighboring patches may not be subdivided to the same level – Cracks can appear because join edges have different control meshes – This can be fixed by adding extra edges Crack 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Computing Normal Vectors • The partial derivative in the s direction is one tangent vector • The partial derivative in the t direction is another • Take their cross product, and normalize, to get the surface normal vector 4/27/04 © University of Wisconsin, CS 559 Spring 2004

Bezier Curve/Surface Problems • To make a long continuous curve with Bezier segments requires using many segments – Same for large surface • Maintaining continuity requires constraints on the control point positions – The user cannot arbitrarily move control vertices and automatically maintain continuity – The constraints must be explicitly maintained – It is not intuitive to have control points that are not free 4/27/04 © University of Wisconsin, CS 559 Spring 2004