KS 091201 MATEMATIKA DISKRIT DISCRETE MATHEMATICS The Fundamentals

KS 091201 MATEMATIKA DISKRIT (DISCRETE MATHEMATICS ) The Fundamentals: Algorithm Discrete Math Team

2 Outline What Algorithm Is. Algorithm 1 : Maximum element Algorithm 2 : Linier Search Algorithm 3 : Binary Search Sorting Algorithm

3 What is an algorithm? An algorithm is “a finite set of precise instructions for performing a computation or for solving a problem” A program is one type of algorithm All programs are algorithms Not all algorithms are programs! Directions to somebody’s house is an algorithm A recipe for cooking a cake is an algorithm The steps to compute the cosine of 90° is an algorithm

4 Algorithm 1: Maximum element Given a list, how do we find the maximum element in the list? To express the algorithm, we’ll use pseudocode Pseudocode is kinda like a programming language, but not really

5 Algorithm 1: Maximum element Algorithm for finding the maximum element in a list: procedure max (a 1, a 2, …, an: integers) max : = a 1 for i : = 2 to n if max < ai then max : = ai {max is the largest element}

6 Algorithm 1: Maximum element procedure max (a 1, a 2, …, an: integers) max : = a 1 for i : = 2 to n if max < ai then max : = ai max a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a 10 4 1 7 0 5 2 9 3 6 8 i 10 9 8 7 6 5 4 3 2 9 7 4

7 Maximum element running time How long does this take? If the list has n elements, worst case scenario is that it takes n “steps” Here, a step is considered a single step through the list

8 Properties of algorithms Algorithms properties: Input: generally share a set of what the algorithm takes in as input Output: what the algorithm produces as output Definiteness: the steps are defined precisely Correctness: should produce the correct output Finiteness: the steps required should be finite Effectiveness: each step must be able to be performed in a finite amount of time Generality: the algorithm should be applicable to all problems of a similar form

9 Searching algorithms Given a list, find a specific element in the list We will see two types Linear search a. k. a. sequential search Binary search

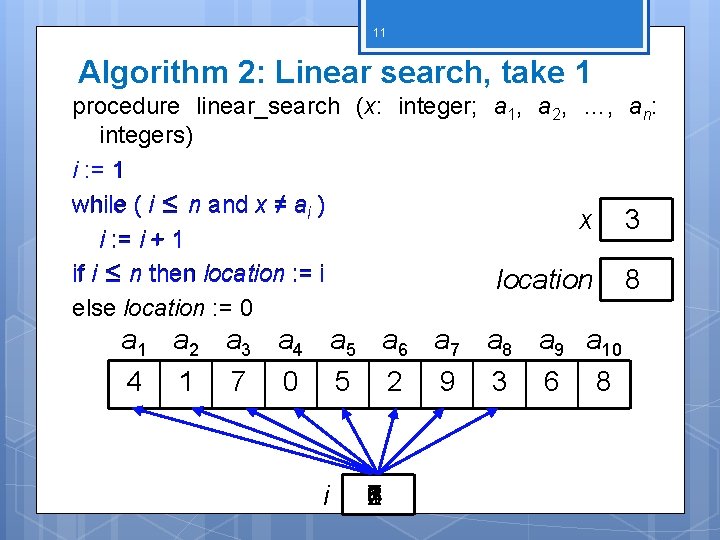
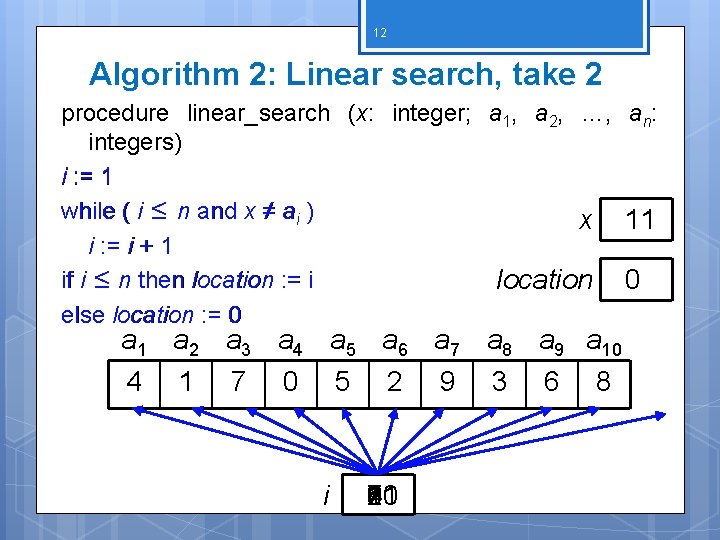
10 Algorithm 2: Linear search Given List a list, find a specific element in the list does NOT have to be sorted! procedure linear_search (x: integer; a 1, a 2, …, an: integers) i : = 1 while ( i ≤ n and x ≠ ai ) i : = i + 1 if i ≤ n then location : = i else location : = 0 {location is the subscript of the term that equals x, or it is 0 if x is not found}

11 Algorithm 2: Linear search, take 1 procedure linear_search (x: integer; a 1, a 2, …, an: integers) i : = 1 while ( i ≤ n and x ≠ ai ) x 3 i : = i + 1 if i ≤ n then location : = i location 8 else location : = 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a 10 4 1 7 0 5 2 9 3 6 8 i 1 8 7 6 5 4 3 2

12 Algorithm 2: Linear search, take 2 procedure linear_search (x: integer; a 1, a 2, …, an: integers) i : = 1 while ( i ≤ n and x ≠ ai ) x 11 i : = i + 1 if i ≤ n then location : = i location 0 else location : = 0 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a 10 4 1 7 0 5 2 9 3 6 8 i 90 8 7 6 5 4 3 2 1 11

13 Linear search running time How long does this take? If the list has n elements, worst case scenario is that it takes n “steps” Here, a step is considered a single step through the list

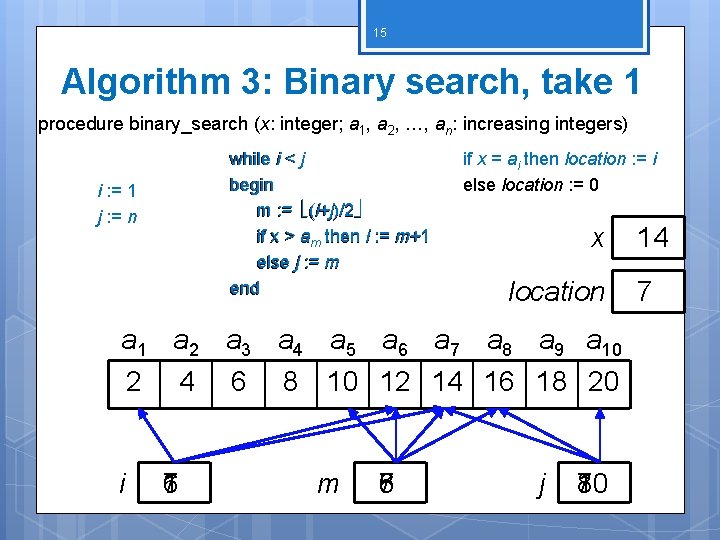
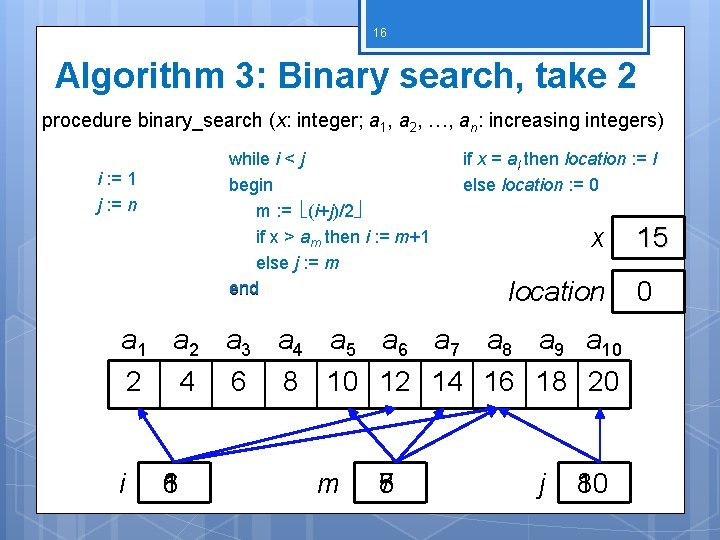
14 Algorithm 3: Binary search Given a list, find a specific element in the list List MUST be sorted! Each time it iterates through, it cuts the list in half procedure binary_search (x: integer; a 1, a 2, …, an: increasing integers) i : = 1 { i is left endpoint of search interval } j : = n { j is right endpoint of search interval } while i < j begin m : = (i+j)/2 { m is the point in the middle } if x > am then i : = m+1 else j : = m end if x = ai then location : = i else location : = 0 {location is the subscript of the term that equals x, or it is 0 if x is not found}

15 Algorithm 3: Binary search, take 1 procedure binary_search (x: integer; a 1, a 2, …, an: increasing integers) while i < j begin m : = (i+j)/2 if x > am then i : = m+1 else j : = m end i : = 1 j : = n if x = ai then location : = i else location : = 0 x location a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a 10 2 4 6 8 10 12 14 16 18 20 i 1 6 7 m 5 8 7 6 j 10 8 7 14 7

16 Algorithm 3: Binary search, take 2 procedure binary_search (x: integer; a 1, a 2, …, an: increasing integers) while i < j begin m : = (i+j)/2 if x > am then i : = m+1 else j : = m end i : = 1 j : = n if x = ai then location : = Ii else location : = 0 x location a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a 10 2 4 6 8 10 12 14 16 18 20 i 1 6 8 m 5 8 7 j 10 8 15 0

17 Binary search running time How long does this take (worst case)? If the list has 8 elements If the list has 16 elements If the list has 64 elements If the list has n elements It takes 3 steps It takes 4 steps It takes 6 steps It takes log 2 n steps

18 Sorting algorithms Given a list, put it into some order Numerical, We lexicographic, etc. will see two types Bubble sort Insertion sort

19 Algorithm 4: Bubble sort One of the most simple sorting algorithms Also one of the least efficient It takes successive elements and “bubbles” them up the list procedure bubble_sort (a 1, a 2, …, an) for i : = 1 to n-1 for j : = 1 to n-i if aj > aj+1 then interchange aj and aj+1 { a 1, …, an are in increasing order }

20 Bubble sort running time Bubble sort algorithm: for i : = 1 to n-1 for j : = 1 to n-i if aj > aj+1 then interchange aj and aj+1 Outer for loop does n-1 iterations Inner for loop does n-1 iterations the first time n-2 iterations the second time … 1 iteration the last time Total: (n-1) + (n-2) + (n-3) + … + 2 + 1 = (n 2 -n)/2 We can say that’s “about” n 2 time

21 Algorithm 5: Insertion sort Another simple (and inefficient) algorithm It starts with a list with one element, and inserts new elements into their proper place in the sorted part of the list procedure insertion_sort (a 1, a 2, …, an) for j : = 2 to n take successive elements in the list begin i : = 1 while aj > ai find where that element should be in i : = i +1 the sorted portion of the list m : = aj for k : = 0 to j-i-1 move all elements in the sorted portion aj-k : = aj-k-1 of the list that are greater than the ai : = m element up by one end { a 1, a 2, …, an are sortedcurrent } put the current element into it’s proper place in the sorted portion of the list

22 Insertion sort running time for j : = 2 to n begin i : = 1 while aj > ai i : = i +1 m : = aj for k : = 0 to j-i-1 aj-k : = aj-k-1 ai : = m end { a 1, a 2, …, an are sorted } Outer for loop runs n-1 times In the inner for loop: Worst case is when the while keeps i at 1, and the for loop runs lots of times If i is 1, the inner for loop runs 1 time (k goes from 0 to 0) on the first iteration, 1 time on the second, up to n-2 times on the last iteration Total is 1 + 2 + … + n-2 = (n-1)(n-2)/2 We can say that’s “about” n 2 time

23 Comparison of running times Searches Linear: n steps Binary: log 2 n steps Binary search is about as fast as you can get Sorts Bubble: n 2 steps Insertion: n 2 steps There are other, more In efficient, sorting techniques principle, the fastest are heap sort, quick sort, and merge sort These each take n * log 2 n steps In practice, quick sort is the fastest, followed by merge sort

24 Example Describe an algorithm that takes as input a list of n integers in nondecreasing order and produces the list of all values that occur more than one.

25 Answer procedure duplicates (a 1, a 2, . . . , an: integers in nondecreasing order) k : = 0 (this count the duplicates) j : = 2 while j ≤ n begin if aj = aj-1 then begin k : = k +1 ck : = aj while (j ≤ n and aj : = ck) j : = j +1 end {c 1, c 2, . . . , ck is the desired list}