Introduzione alle equazioni di Maxwell Gauss Maxwell Faraday

Introduzione alle equazioni di Maxwell Gauss Maxwell Faraday Ampere

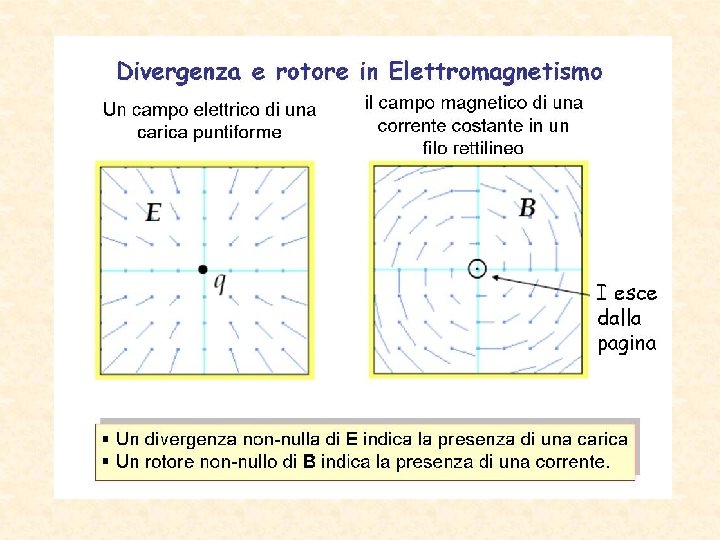
Per caratterizzare un campo vettoriale serve capire come “fluisce” e come “circola”, cioè serve conoscere il rotore e la divergenza. Helmholtz

ingredienti Teorema della media q circuitazione = integrale curvilineo di un campo vettoriale lungo una curva chiusa; componenti tangenziali rotore (teorema di Stokes) q flusso di un campo vettoriale attraverso superfici chiuse ed aperte; componenti normali, divergenza (teorema di Gauss)

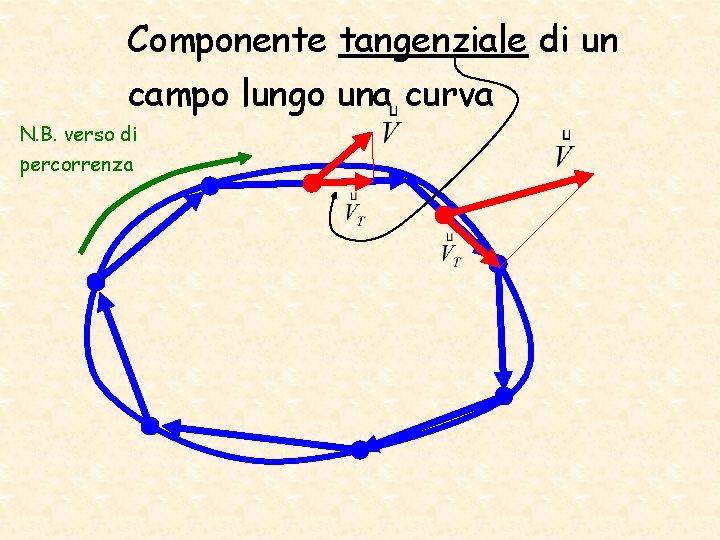
Componente tangenziale di un campo lungo una curva N. B. verso di percorrenza

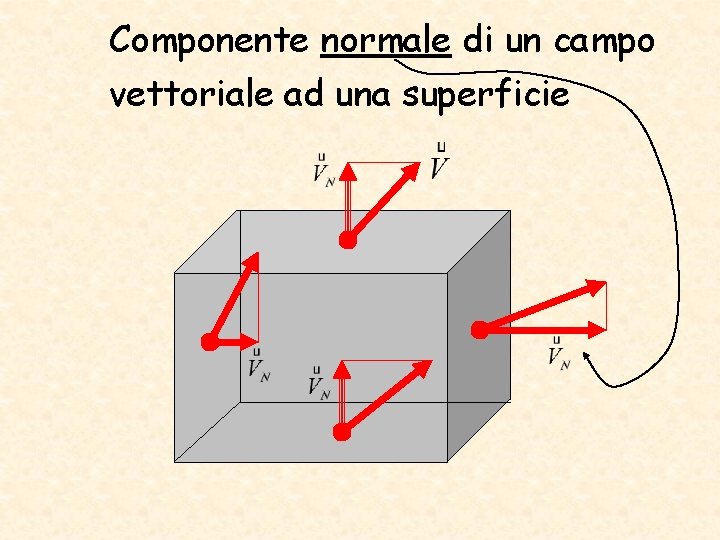
Componente normale di un campo vettoriale ad una superficie

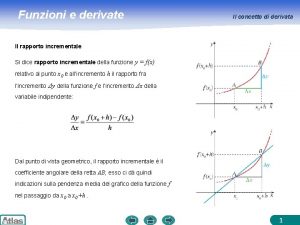
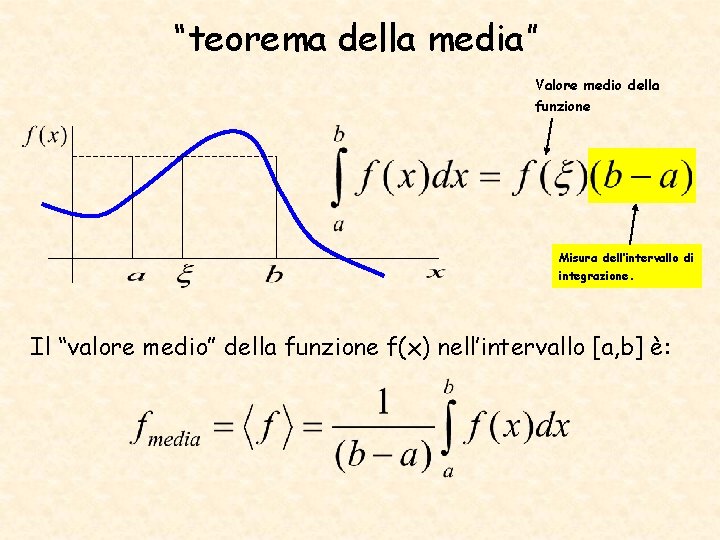
“teorema della media” Valore medio della funzione Misura dell’intervallo di integrazione. Il “valore medio” della funzione f(x) nell’intervallo [a, b] è:

il flusso, la circuitazione (teorema della media) Flusso di attraverso una superficie chiusa S (area di S) Misura dell’insieme di integrazione. circuitazione di lungo una curva chiusa C (lunghezza di C)

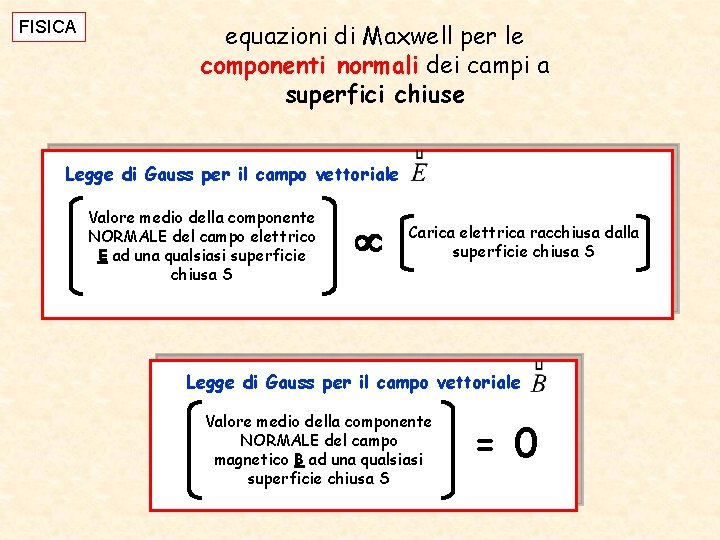
FISICA equazioni di Maxwell per le componenti normali dei campi a superfici chiuse Legge di Gauss per il campo vettoriale Valore medio della componente NORMALE del campo elettrico E ad una qualsiasi superficie chiusa S Carica elettrica racchiusa dalla superficie chiusa S Legge di Gauss per il campo vettoriale Valore medio della componente NORMALE del campo magnetico B ad una qualsiasi superficie chiusa S = 0

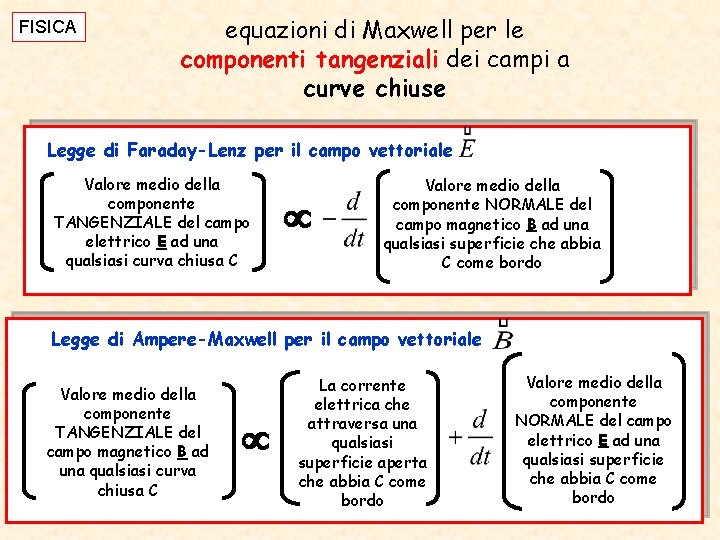
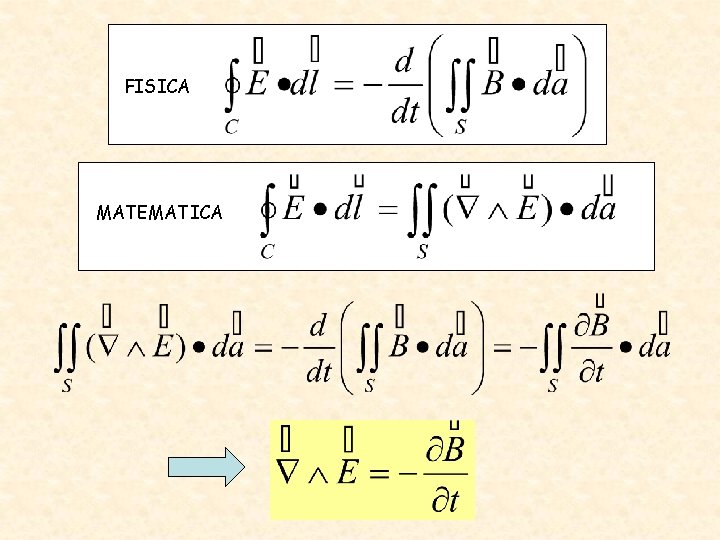
FISICA equazioni di Maxwell per le componenti tangenziali dei campi a curve chiuse Legge di Faraday-Lenz per il campo vettoriale Valore medio della componente TANGENZIALE del campo elettrico E ad una qualsiasi curva chiusa C Valore medio della componente NORMALE del campo magnetico B ad una qualsiasi superficie che abbia C come bordo Legge di Ampere-Maxwell per il campo vettoriale Valore medio della componente TANGENZIALE del campo magnetico B ad una qualsiasi curva chiusa C La corrente elettrica che attraversa una qualsiasi superficie aperta che abbia C come bordo Valore medio della componente NORMALE del campo elettrico E ad una qualsiasi superficie che abbia C come bordo

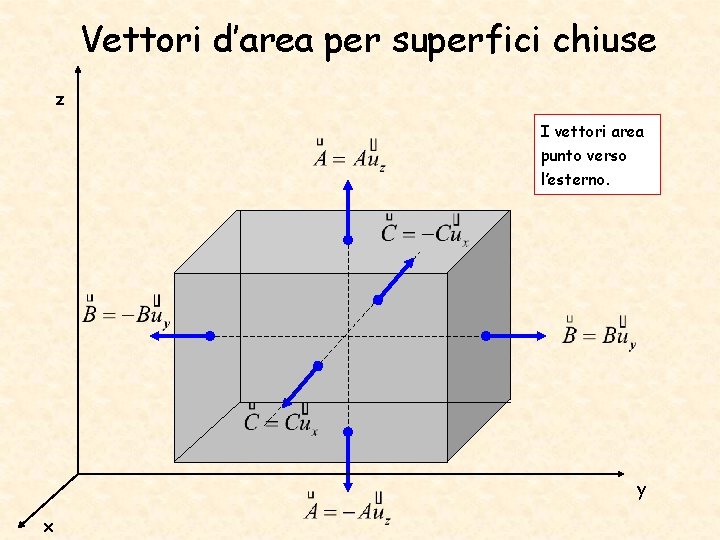
Vettori d’area per superfici chiuse z I vettori area punto verso l’esterno. y x

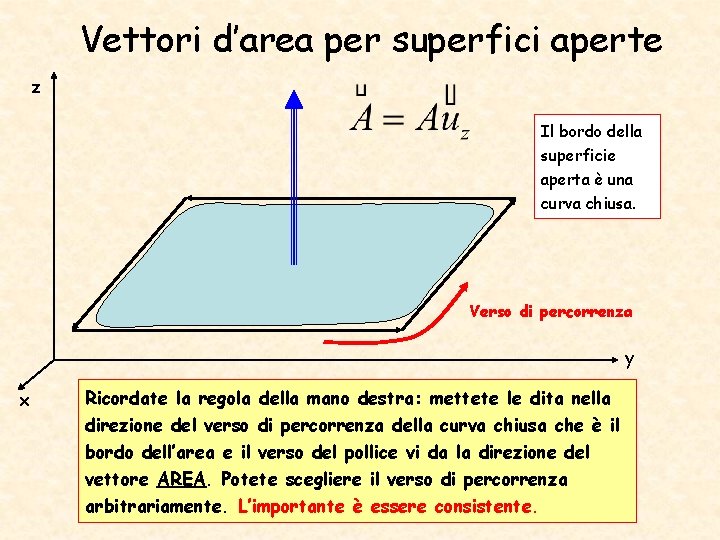
Vettori d’area per superfici aperte z Il bordo della superficie aperta è una curva chiusa. Verso di percorrenza y x Ricordate la regola della mano destra: mettete le dita nella direzione del verso di percorrenza della curva chiusa che è il bordo dell’area e il verso del pollice vi da la direzione del vettore AREA. Potete scegliere il verso di percorrenza arbitrariamente. L’importante è essere consistente.

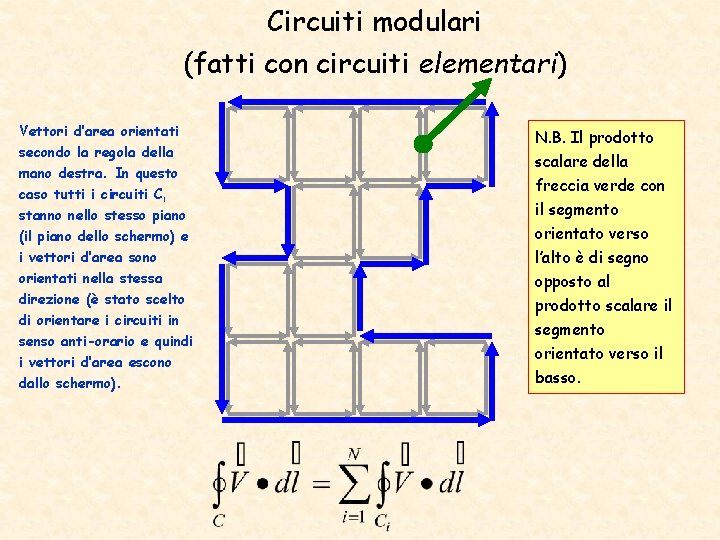
Circuiti modulari (fatti con circuiti elementari) Vettori d’area orientati secondo la regola della mano destra. In questo caso tutti i circuiti Ci stanno nello stesso piano (il piano dello schermo) e i vettori d’area sono orientati nella stessa direzione (è stato scelto di orientare i circuiti in senso anti-orario e quindi i vettori d’area escono dallo schermo). N. B. Il prodotto scalare della freccia verde con il segmento orientato verso l’alto è di segno opposto al prodotto scalare il segmento orientato verso il basso.

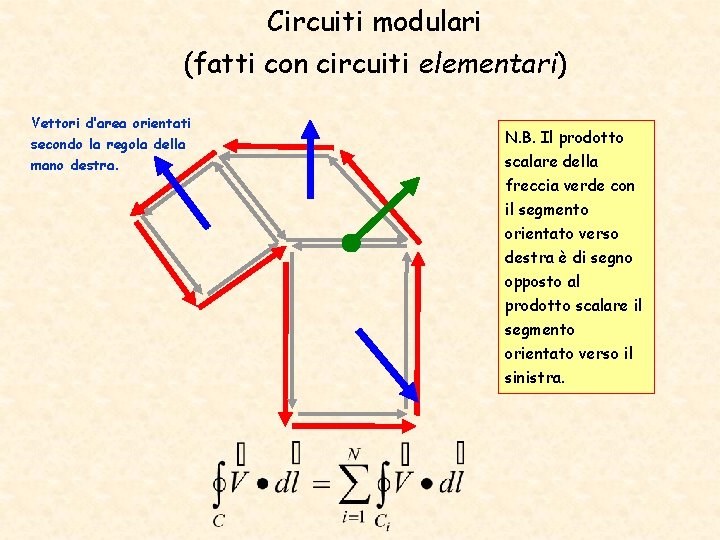
Circuiti modulari (fatti con circuiti elementari) Vettori d’area orientati secondo la regola della mano destra. N. B. Il prodotto scalare della freccia verde con il segmento orientato verso destra è di segno opposto al prodotto scalare il segmento orientato verso il sinistra.

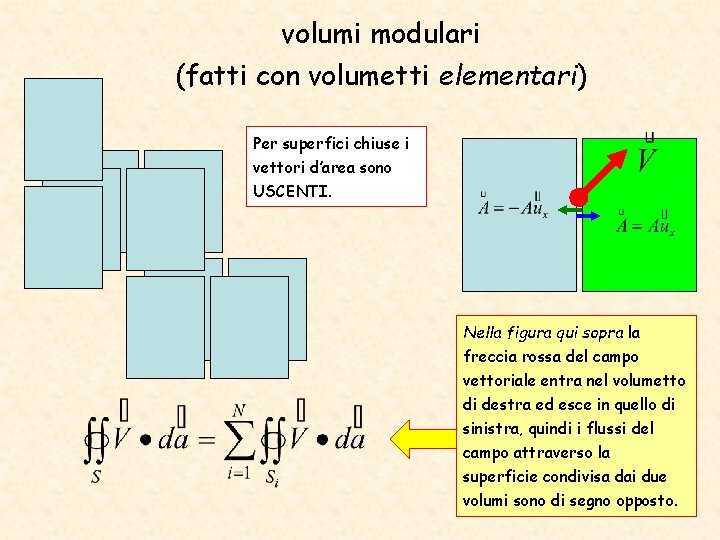
volumi modulari (fatti con volumetti elementari) Per superfici chiuse i vettori d’area sono USCENTI. Nella figura qui sopra la freccia rossa del campo vettoriale entra nel volumetto di destra ed esce in quello di sinistra, quindi i flussi del campo attraverso la superficie condivisa dai due volumi sono di segno opposto.

Teoria dell’elettromagnetismo in forma integrale: Carica interna alla superficie S (nel volume V) FISICA Legge di Gauss per il campo E Legge di Gauss per il campo B Legge di Lorentz Legge di Faraday-Lenz Legge di Ampere-Maxwell Corrente elettrica I che buca la superficie S (che è concatenata da C) Corrente di “spostamento”

MATEMATICA Teorema di Stokes (teorema del rotore) Superficie aperta S con buco. Il buco ha bordo C. buco “La circuitazione di un campo vettoriale lungo una qualsiasi curva chiusa C è uguale al flusso del rotore attraverso qualsiasi superficie aperta (bucato) che ha C come bordo del buco. Il verso di percorrenza della curva C e l’orientazione dei vettori di area sono legati dalla regola della mano destra. ”

MATEMATICA Teorema di Stokes (teorema del rotore) Superficie aperta S con buco. Il buco ha bordo C. buco Ricordate la regola della mano destra: mettete le dita nella direzione del verso di percorrenza del circuito C e il pollice sarà nella direzione del vettore AREA. Potete scegliere il verso di percorrenza arbitrariamente. L’importante è essere consistente. Qualsiasi superficie aperta S che abbia C come bordo (“che sia appoggia su C”)

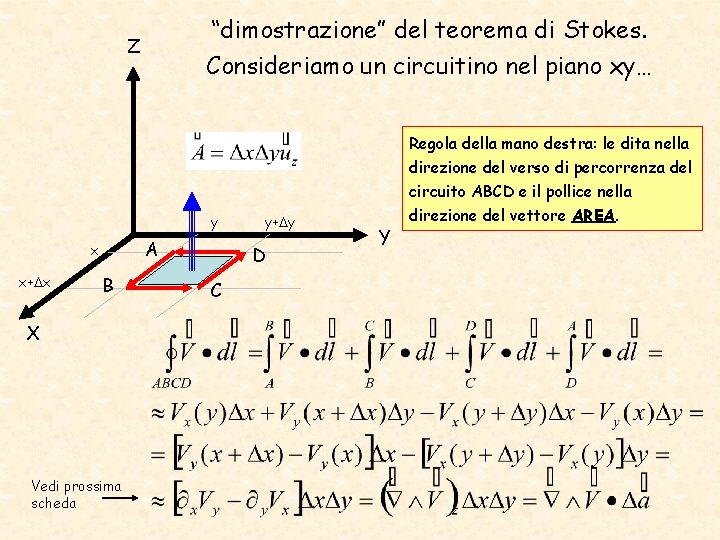
“dimostrazione” del teorema di Stokes. Consideriamo un circuitino nel piano xy… Z y A x x+ x B X Vedi prossima scheda y+ y D C Y Regola della mano destra: le dita nella direzione del verso di percorrenza del circuito ABCD e il pollice nella direzione del vettore AREA.

Derivate parziali Rapporto incrementale della funzione Vy variando solo la x quindi

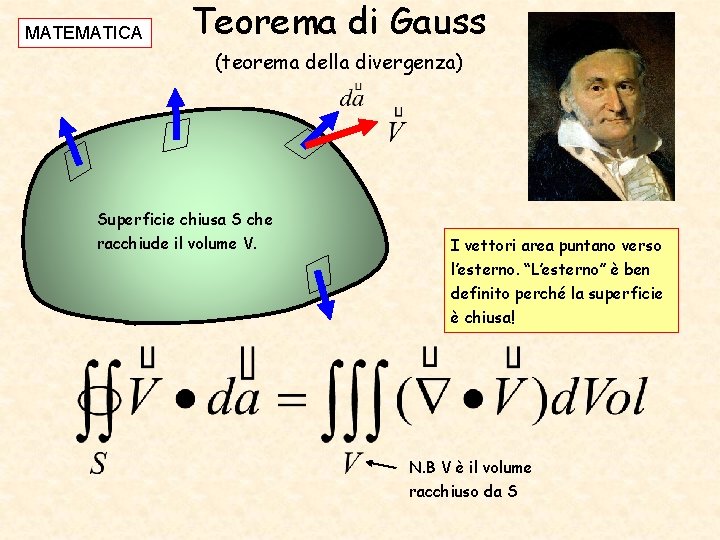
MATEMATICA Teorema di Gauss (teorema della divergenza) Superficie chiusa S che racchiude il volume V. “Il flusso di un campo vettoriale attraverso una qualsiasi superficie chiusa S (senza buchi) è uguale all’integrale di volume della divergenza. ”

MATEMATICA Teorema di Gauss (teorema della divergenza) Superficie chiusa S che racchiude il volume V. I vettori area puntano verso l’esterno. “L’esterno” è ben definito perché la superficie è chiusa! N. B V è il volume racchiuso da S

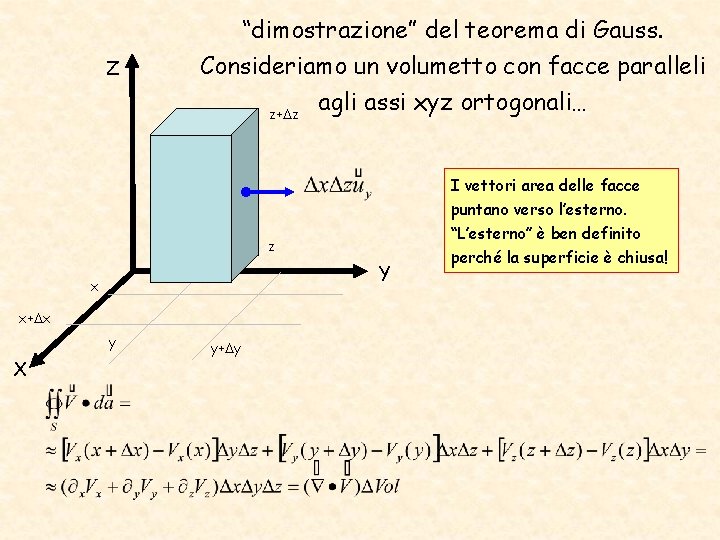
Z “dimostrazione” del teorema di Gauss. Consideriamo un volumetto con facce paralleli agli assi xyz ortogonali… z+ z z Y x x+ x y X y+ y I vettori area delle facce puntano verso l’esterno. “L’esterno” è ben definito perché la superficie è chiusa!

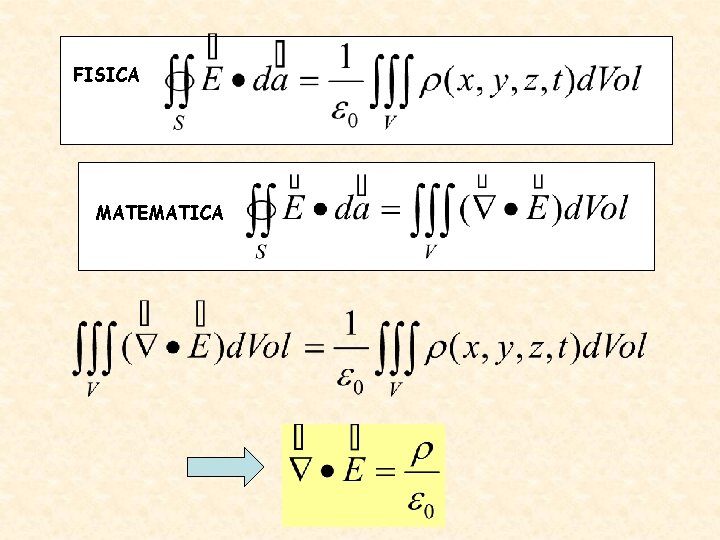
Per i teoremi di Gauss e Stokes le equazioni di Maxwell si possono scrivere in forma differenziale: divergenze rotori FISICA

FISICA MATEMATICA

FISICA MATEMATICA