Introduction to PCP and Hardness of Approximation Dana

Introduction to PCP and Hardness of Approximation Dana Moshkovitz Princeton University and The Institute for Advanced Study 1

This Talk A Groundbreaking Discovery! (From 1991 -2) The PCP Theorem and Hardness of Approximation 2

A Canonical Optimization Problem MAX-3 SAT: Given a 3 CNF Á, what fraction of the clauses can be satisfied simultaneously? Á = (x 7 : x 12 x 1) Æ … Æ (: x 5 : x 9 x 28) x 1 x 5 xn-3 x 2 x 6 x 3 x 7 xn-1 x 4 x 8 xn . . . xn-2 3

Good Assignment Exists Claim: There must exist an assignment that satisfies at least 7/8 fraction of clauses. Proof: Consider a random assignment. . x 1 x 2 x 3 . . xn 4

1. Find the Expectation Let Yi be the random variable indicating whether the i-th clause is satisfied. For any 1 i m, FFFF F F TT FTFT F TTT TFFT TF TT TTFT TTTT 5

1. Find the Expectation The number of clauses satisfied is a random variable Y= Yi. By the linearity of the expectation: E[Y] = E[ Yi] = E[Yi] = 7/8 m 6

2. Conclude Existence Thus, there exists an assignment which satisfies at least the expected fraction (7/8) of clauses. 7

®-Approximation (Max Version) For every input x, computed value C(x): ® ¢ OPT(x) · C(x) · OPT(x) Corollary: There is an efficient ⅞-approximation algorithm for MAX-3 SAT. 8

Better Approximation? Fact: An efficient tighter than ⅞-approximation algorithm is not known. Our Question: Can we prove that if P≠NP such algorithm does not exist? ? 9

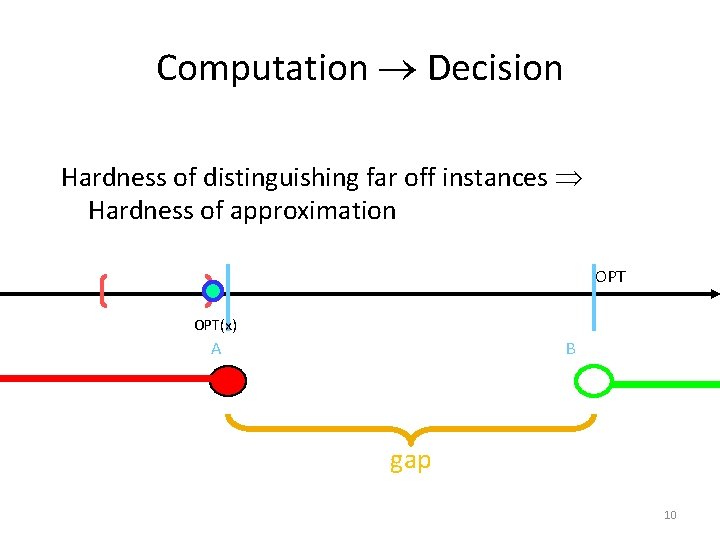
Computation Decision Hardness of distinguishing far off instances Hardness of approximation OPT(x) A B gap 10

Gap Problems (Max Version) • Instance: … • Problem: to distinguish between the following two cases: The maximal solution ≥ B The maximal solution < A 11

Gap NP-Hard Approximation NP-hard Claim: If the [A, B]-gap version of a problem is NP-hard, then that problem is NP-hard to approximate to within factor A/B. 12

Gap NP-Hard Approximation NP-hard Proof (for maximization): Suppose there is an approximation algorithm that, for every x, outputs C(x) ≤ OPT so that C(x) ≥ A/B¢OPT. Distinguisher(x): * If C(x) ≥ A, return ‘YES’ * Otherwise return ‘NO’ A B 13

Gap NP-Hard Approximation NP-hard (1) If OPT(x) ≥ B (the correct answer is ‘YES’), then necessarily, C(x) ≥ A/B¢OPT(x) ≥ A/B·B = A (we answer ‘YES’) (2) If OPT(x)<A (the correct answer is ‘NO’), then necessarily, C(x) ≤ OPT(x) < A (we answer ‘NO’). 14

New Focus: Gap Problems Can we prove that gap-MAX-3 SAT is NP-hard? 15

Connection to Probabilistic Checking of Proofs [FGLSS 91, AS 92, ALMSS 92] Claim: If [A, 1]-gap-MAX-3 SAT is NP-hard, then every NP language L has a probabilistically checkable proof (PCP): There is an efficient randomized verifier that queries 3 proof symbols: • x L: There exists a proof that is always accepted. • x L: For any proof, the probability to err and accept is ≤A. Note: Can get error probability ² by making O(log 1/²) queries. 16

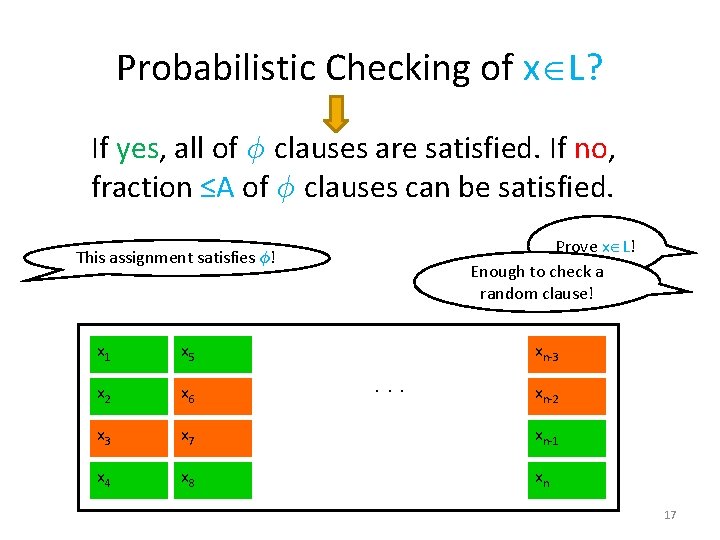
Probabilistic Checking of x L? If yes, all of Á clauses are satisfied. If no, fraction ≤A of Á clauses can be satisfied. Prove x L! Enough to check a random clause! This assignment satisfies Á! x 1 x 5 xn-3 x 2 x 6 x 3 x 7 xn-1 x 4 x 8 xn . . . xn-2 17

Other Direction: PCP Gap-MAX-3 SAT NP-Hard • Note: Every predicate on O(1) Boolean variables can be written as a conjunction of O(1) 3 -clauses on the same variables, as well as, perhaps, O(1) more variables. – If the predicate is satisfied, then there exists an assignment for the additional variables, so that all 3 -clauses are satisfied. – If the predicate is not satisfied, then for any assignment to the additional variables, at least one 3 -clause is not satisfied. 18

The PCP Theorem […, AS 92, ALMSS 92]: Every NP language L has a probabilistically checkable proof (PCP): There is an efficient randomized verifier that queries O(1) proof symbols: x L: There exists a proof that is always accepted. x L: For any proof, the probability to accept is ≤½. Remark: Elegant combinatorial proof by Dinur, 05. 19

Conclusion Probabilistic Checking of Proofs (PCP) Hardness of Approximation 20

Tight Inapproximability? • Corollary: NP-hard to approximate MAX-3 SAT to within some constant factor. • Question: Can we get tight ⅞-hardness? 21

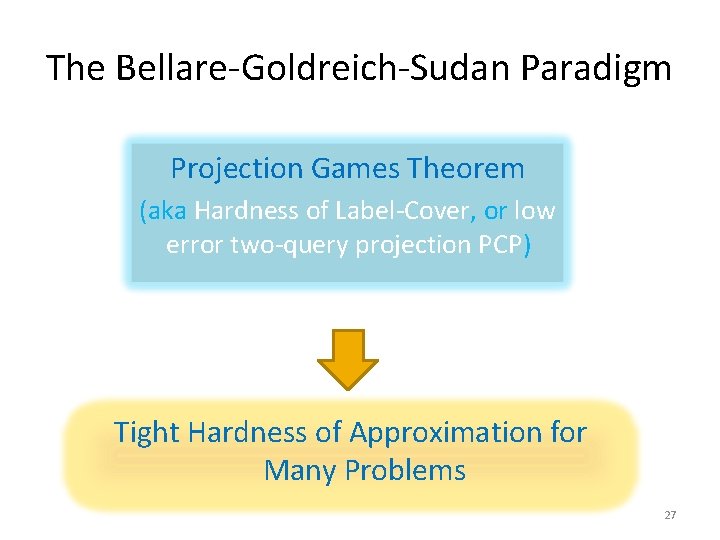
The Bellare-Goldreich-Sudan Paradigm, 1995 Projection Games Theorem (aka Hardness of Label-Cover, or low error two-query projection PCP) Long-code based reduction Tight Hardness of Approximating 3 SAT [Håstad 97] 22

The Bellare-Goldreich-Sudan Paradigm, 1995 Projection Games Theorem (aka Hardness of Label-Cover, or low error two-query projection PCP) Long-code based reduction e. g. , Set-Cover [Feige 96] Tight Hardness of Approximation for Many Problems 23

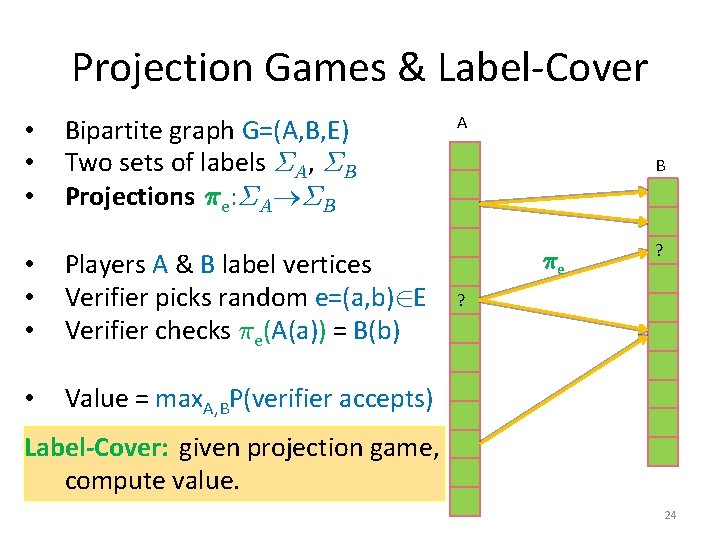
Projection Games & Label-Cover • • • Bipartite graph G=(A, B, E) Two sets of labels §A, §B Projections ¼e: §A §B • • • Players A & B label vertices Verifier picks random e=(a, b)2 E Verifier checks ¼e(A(a)) = B(b) • Value = max. A, BP(verifier accepts) A B ¼e ? ? Label-Cover: given projection game, compute value. 24

Equivalent Formulation of PCP Thm Theorem […, AS 92, ALMSS 92]: NP-hard to approximate Label-Cover within some constant. Proof: by reduction to Label. Cover (see picture). Verifier randomness Proof entries s… Verifier querie n = eck o i ct ch e j y Pro tenc sis n o c symbol Accepting verifier view 25

Projection Games Theorem: Low Error PCP Theorem Claim: There is an efficient 1/k-approximation algorithm for projection games on k labels (i. e. , |§A|, |§B|·k). Projection Games Theorem For every ²>0, there is k=k(²), such that it is NPhard to decide for a given projection game on k labels whether its value = 1 or < ². 26

The Bellare-Goldreich-Sudan Paradigm Projection Games Theorem (aka Hardness of Label-Cover, or low error two-query projection PCP) Tight Hardness of Approximation for Many Problems 27

How To Prove The Projection Games Theorem? [AS 92, ALMSS 92] PCP Theorem Parallel repetition Theorem [Raz 94] ? ? [M-Raz 08] Construction Projection Games Theorem Hardness of Approximation 28

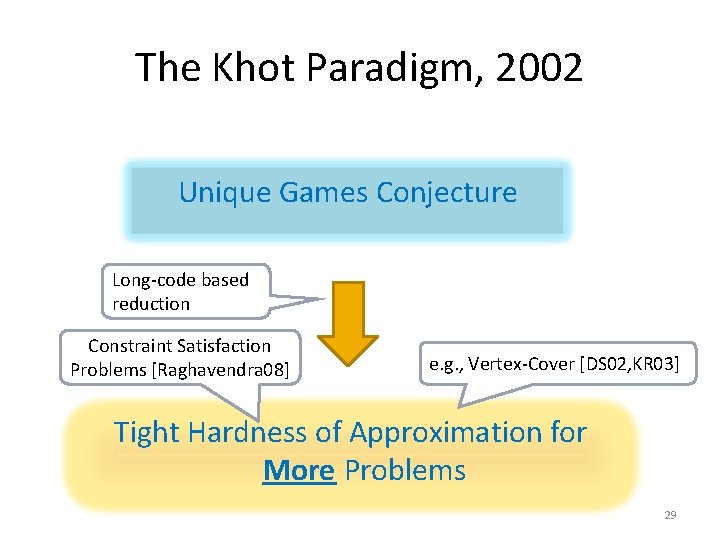
The Khot Paradigm, 2002 Unique Games Conjecture Long-code based reduction Constraint Satisfaction e. g. , Max-Cut [KKMO 05] Problems [Raghavendra 08] e. g. , Vertex-Cover [DS 02, KR 03] Tight Hardness of Approximation for More Problems 29

Thank You! 30