Introduction to Algorithms Amortized Analysis Introduction to Algorithms

Introduction to Algorithms: Amortized Analysis

Introduction to Algorithms Amortized Analysis • Dynamic tables • Aggregate method • Accounting method • Potential method • Binary Counter • Multi-pop Stack CS 421 - Introduction to Algorithms 2

How large should a Hash Table be? Goal: Make the table as small as possible, but large enough so that it won’t overflow. Problem: What if we don’t know the proper size in advance? Solution: Dynamic tables. IDEA: Whenever the table overflows, “grow” it by allocating (via malloc or new) a new, larger table. Move all items from the old table into the new one, and free the storage for the old table. CS 421 - Introduction to Algorithms 3

1. INSERT 2. INSERT 1 overflow CS 421 - Introduction to Algorithms 4

Example of a Dynamic Table 1. INSERT 2. INSERT 11 overflow CS 421 - Introduction to Algorithms 5

Example of a Dynamic Table 1. INSERT 2. INSERT 11 2 CS 421 - Introduction to Algorithms 6

Example of a Dynamic Table 1. INSERT 2. INSERT 3. INSERT 11 22 overflow CS 421 - Introduction to Algorithms 7

Example of a Dynamic Table 1. INSERT 2. INSERT 3. INSERT 1 2 overflow CS 421 - Introduction to Algorithms 8

Example of a Dynamic Table 1. INSERT 2. INSERT 3. INSERT 1 2 CS 421 - Introduction to Algorithms 9

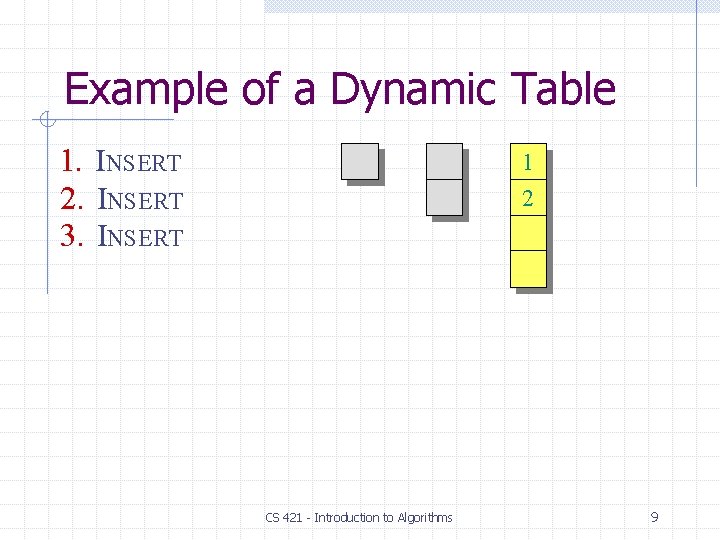
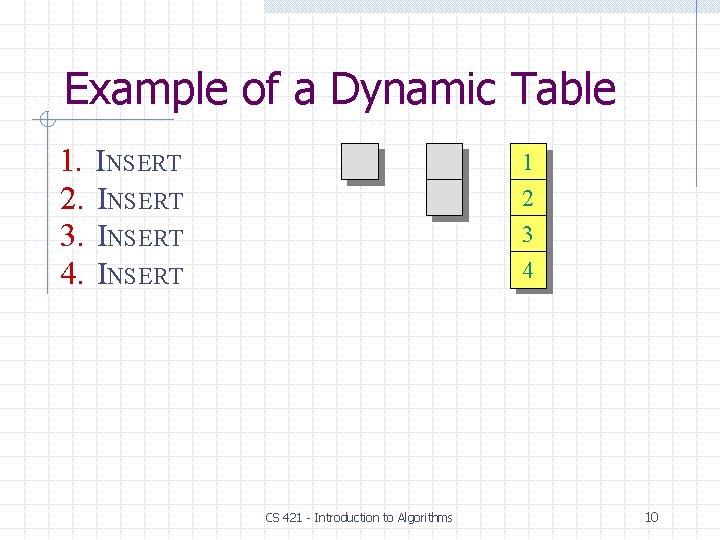
Example of a Dynamic Table 1. 2. 3. 4. INSERT 1 2 3 4 CS 421 - Introduction to Algorithms 10

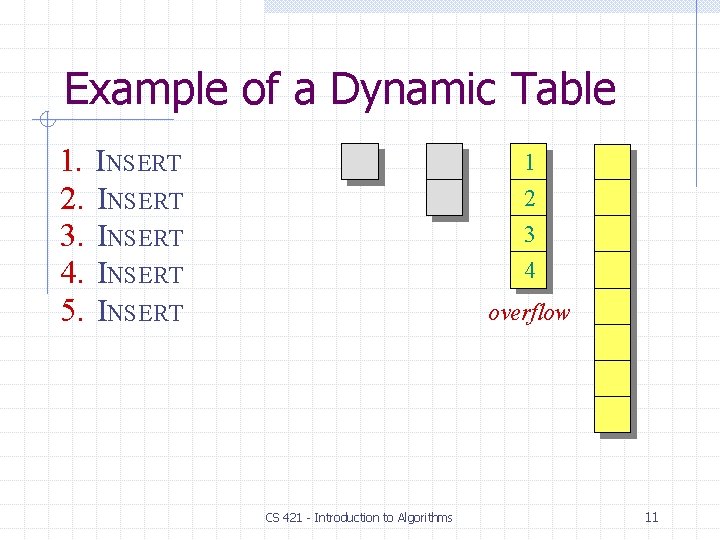
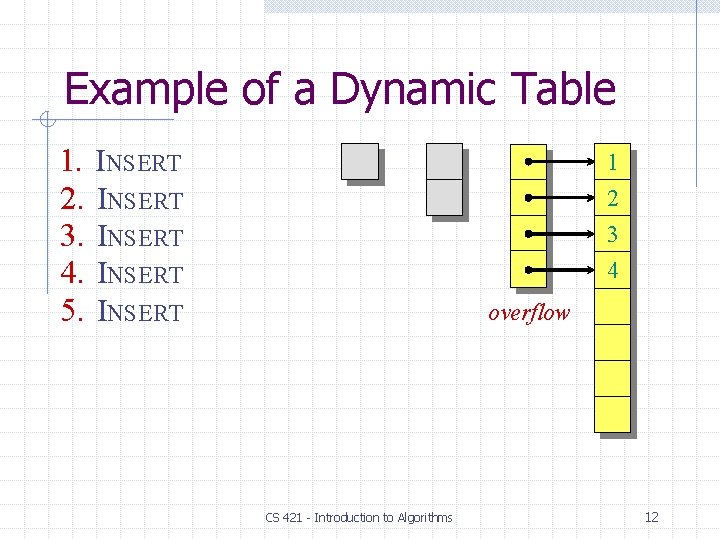
Example of a Dynamic Table 1. 2. 3. 4. 5. INSERT INSERT 1 2 3 4 overflow CS 421 - Introduction to Algorithms 11

Example of a Dynamic Table 1. 2. 3. 4. 5. INSERT INSERT 1 2 3 4 overflow CS 421 - Introduction to Algorithms 12

Example of a Dynamic Table 1. 2. 3. 4. 5. INSERT INSERT 1 2 3 4 CS 421 - Introduction to Algorithms 13

Example of a Dynamic Table 1. 2. 3. 4. 5. 6. 7. INSERT INSERT 1 2 3 4 5 6 7 CS 421 - Introduction to Algorithms 14

Worst-Case Analysis Consider a sequence of n insertions. The worst-case time to execute one insertion is (n). Therefore, the worst-case time for n insertions is n · (n) = (n 2). CS 421 - Introduction to Algorithms 15

Worst-Case Analysis Consider a sequence of n insertions. The worst-case time to execute one insertion is (n). Therefore, the worst-case time for n insertions is n · (n) = (n 2). WRONG! In fact, the worst-case cost for n insertions is only (n) ≪ (n 2). Let’s see why. CS 421 - Introduction to Algorithms 16

Tighter Analysis Let ci = the cost of the i th insertion i if i – 1 is an exact power of 2, = 1 otherwise. i 1 2 3 4 5 6 7 8 9 sizei 1 2 4 4 8 8 16 16 ci 1 2 3 1 5 1 1 1 9 CS 421 - Introduction to Algorithms 10 1 17

Tighter Analysis Let ci = the cost of the i th insertion i if i – 1 is an exact power of 2, = 1 otherwise. i 1 2 3 4 5 6 7 8 9 sizei 1 2 4 4 8 8 16 16 ci 1 1 2 1 1 4 1 1 8 CS 421 - Introduction to Algorithms 10 1 18

Tighter Analysis (cont'd) n Cost of n insertions ci i 1 n lg(n-1) j 0 2 j 3 n (n). Thus, the average cost of each dynamic table operation is (n)/n = (1). CS 421 - Introduction to Algorithms 19

Amortized Analysis An amortized analysis is any strategy for analyzing a sequence of operations to show that the average cost per operation is small, even though a single operation within the sequence might be expensive. Even though we’re taking averages, however, probability is not involved! • An amortized analysis guarantees the average performance of each operation in the worst case. CS 421 - Introduction to Algorithms 20

Types of Amortized Analyses Three common amortization arguments: • the aggregate method, • the accounting method, • the potential method. We’ve just seen an aggregate analysis. The aggregate method, though simple, lacks the precision of the other two methods. In particular, the accounting and potential methods allow a specific amortized cost to be allocated to each operation. 21 CS 421 - Introduction to Algorithms

Accounting Method • Charge i th operation a fictitious amortized cost ĉi, where $1 pays for 1 unit of work (i. e. , time). • This fee is consumed to perform the operation. • Any amount not immediately consumed is stored in the bank for use by subsequent operations. • The bank balance must not go negative! We must n n ensure that ci c i i 1 for all n. • Thus, the total amortized costs provide an upper bound on the total true costs. CS 421 - Introduction to Algorithms 22

Accounting Analysis: Dynamic Tables Charge an amortized cost of ĉi = $3 for the i th insertion. • $1 pays for the immediate insertion. • $2 is stored for later table doubling. When the table doubles, $1 pays to move a recent item, and $1 pays to move an old item. Example: $0 $0 $0 $2 $2 $2 overflow $0 $0 $0 CS 421 - Introduction to Algorithms 23

Accounting Analysis: Dynamic Tables Charge an amortized cost of ĉi = $3 for the i th insertion. • $1 pays for the immediate insertion. • $2 is stored for later table doubling. When the table doubles, $1 pays to move a recent item, and $1 pays to move an old item. Example: $0 $0 $2 $2 overflow $0 $0 $2 $2 CS 421 - Introduction to Algorithms 24

Accounting Analysis: Dynamic Tables Charge an amortized cost of ĉi = $3 for the i th insertion. • $1 pays for the immediate insertion. • $2 is stored for later table doubling. When the table doubles, $1 pays to move a recent item, and $1 pays to move an old item. Example: $0 $0 $2 $2 $0 $0 $2 $2 $2 CS 421 - Introduction to Algorithms 25

Accounting Analysis (cont'd) Key invariant: Bank balance never drops below 0. Thus, the sum of the amortized costs provides an upper bound on the sum of the true costs. i 1 2 3 4 5 6 7 8 9 sizei 1 2 4 4 8 8 16 16 ci 1 2 3 1 5 1 1 1 9 1 ĉi 2* 3 3 3 3 3 1 2 4 6 8 2 4 banki 2 10 *Okay, so I lied. The first operation costs only $2, not $3. CS 421 - Introduction to Algorithms 26

Potential Method IDEA: View the bank account as the potential energy (à la physics) of the dynamic set. Framework: • Start with an initial data structure D 0. • Operation i transforms Di– 1 to Di. • The cost of operation i is ci. • Define a potential function : {Di} R, such that (D 0 ) = 0 and (Di ) 0 for all i. • The amortized cost ĉi with respect to is defined to be ĉi = ci + (Di) – (Di– 1). CS 421 - Introduction to Algorithms 27

Understanding Potentials ĉi = ci + (Di) – (Di– 1) potential difference i • If i > 0, then ĉi > ci. Operation i stores work in the data structure for later use. • If i < 0, then ĉi < ci. The data structure delivers up stored work to help pay for operation i. CS 421 - Introduction to Algorithms 28

Amortized Costs Bound True Costs The total amortized cost of n operations is n n i 1 c i ci (Di ) (Di 1 ) Summing both sides. CS 421 - Introduction to Algorithms 29

Amortized Costs Bound True Costs The total amortized cost of n operations is n n i 1 c i ci (Di ) (Di 1 ) n ci (Dn ) (D 0 ) i 1 The series telescopes. CS 421 - Introduction to Algorithms 30

Amortized Costs Bound True Costs The total amortized cost of n operations is n n i 1 c i ci (Di ) (Di 1 ) n ci (Dn ) (D 0 ) i 1 n ci i 1 since (Dn) 0 and (D 0 ) = 0. CS 421 - Introduction to Algorithms 31

Potential Analysis: Table Doubling Define the potential of the table after the ith insertion by (Di) = 2 i – 2�lg i� (Assume 2 �lg 0� = 0). Note: • (D 0 ) = 0 • (Di) 0 for all i. Example: • • • • ( $0 $0 $2 $2 = 2· 6 – 23 = 4 accounting method) CS 421 - Introduction to Algorithms 32

Calculation of Amortized Costs The amortized cost of the i th insertion is ĉi = ci + (Di) – (Di– 1) CS 421 - Introduction to Algorithms 33

Calculation of Amortized Costs The amortized cost of the i th insertion is ĉi = ci + (Di) – (Di– 1) = i if i – 1 is an exact power of 2 1 otherwise + (2 i – 2�lg i�)– (2(i – 1) – 2�lg (i – 1)� ) CS 421 - Introduction to Algorithms 34

Calculation of Amortized Costs The amortized cost of the i th insertion is ĉi = ci + (Di) – (Di– 1) = i if i – 1 is an exact power of 2 1 otherwise + (2 i – 2�lg i�)– (2(i – 1) – 2�lg (i – 1)� = ) i if i – 1 is an exact power of 2 1 otherwise + 2 – 2�lg i�+ 2�lg (i – 1)� CS 421 - Introduction to Algorithms 35

Calculation Case 1: i – 1 is an exact power of 2. CS 421 - Introduction to Algorithms 36

Calculation Case 1: i – 1 is an exact power of 2. �lg i � �lg (i – 1)� +2 ĉi = i + 2 – 2 CS 421 - Introduction to Algorithms 37

Calculation Case 1: i – 1 is an exact power of 2. �lg i � �lg (i – 1)� +2 ĉi = i + 2 – 2(i – 1) + (i – 1) CS 421 - Introduction to Algorithms 38

Calculation Case 1: i – 1 is an exact power of 2. �lg i � �lg (i – 1)� +2 ĉi = i + 2 – 2(i – 1) + (i – 1) = i + 2 – 2 i + 2 + i – 1 CS 421 - Introduction to Algorithms 39

Calculation Case 1: i – 1 is an exact power of 2. �lg i � �lg (i – 1)� +2 ĉi = i + 2 – 2(i – 1) + (i – 1) = i + 2 – 2 i + 2 + i – 1 =3 CS 421 - Introduction to Algorithms 40

Calculation Case 1: i – 1 is an exact power of 2. �lg i � �lg (i – 1)� +2 ĉi = i + 2 – 2(i – 1) + (i – 1) = i + 2 – 2 i + 2 + i – 1 =3 Case 2: i – 1 is not an exact power of 2. CS 421 - Introduction to Algorithms 41

Calculation Case 1: i – 1 is an exact power of 2. lg i �lg (i – 1)� ĉi = i + 2 – 2 + 2 = i + 2 – 2(i – 1) + (i – 1) = i + 2 – 2 i + 2 + i – 1 =3 Case 2: i – 1 is not an exact power of 2. �lg i � �lg (i – 1)� +2 ĉi = 1 + 2 – 2 CS 421 - Introduction to Algorithms 42

Calculation Case 1: i – 1 is an exact power of 2. lg i �lg (i – 1)� ĉi = i + 2 – 2 + 2 = i + 2 – 2(i – 1) + (i – 1) = i + 2 – 2 i + 2 + i – 1 =3 Case 2: i – 1 is not an exact power of 2. �lg i � �lg (i – 1)� +2 ĉi = 1 + 2 – 2 =3 (since 2�lg i � = 2�lg (i – 1)� ) CS 421 - Introduction to Algorithms 43

Calculation Case 1: i – 1 is an exact power of 2. lg i �lg (i – 1)� ĉi = i + 2 – 2 + 2 = i + 2 – 2(i – 1) + (i – 1) = i + 2 – 2 i + 2 + i – 1 =3 Case 2: i – 1 is not an exact power of 2. lg i �lg (i – 1)� ĉi = 1 + 2 – 2 + 2 =3 (since 2 lg i = 2�lg (i – 1)�) Therefore, n insertions cost (n) in the worst case. CS 421 - Introduction to Algorithms 44

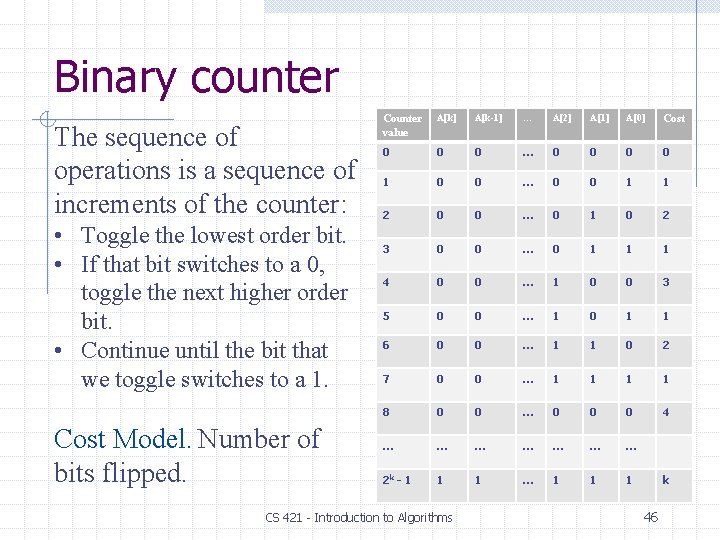
Binary counter Goal. Increment a k-bit binary counter (mod 2 k). Representation. aj = jth least significant bit of counter. Counter value A[k] A[k-1] … A[2] A[1] A[0] 0 0 0 … 0 0 0 1 0 0 … 0 0 1 2 0 0 … 0 1 0 3 0 0 … 0 1 1 4 0 0 … 1 0 0 5 0 0 … 1 0 1 6 0 0 … 1 1 0 7 0 0 … 1 1 1 8 0 0 … 0 0 0 … … … … 2 k - 1 1 1 … 1 1 1 CS 421 - Introduction to Algorithms 45

Binary counter The sequence of operations is a sequence of increments of the counter: • Toggle the lowest order bit. • If that bit switches to a 0, toggle the next higher order bit. • Continue until the bit that we toggle switches to a 1. Cost Model. Number of bits flipped. Counter value A[k] A[k-1] … A[2] A[1] A[0] Cost 0 0 0 … 0 0 1 1 2 0 0 … 0 1 0 2 3 0 0 … 0 1 1 1 4 0 0 … 1 0 0 3 5 0 0 … 1 0 1 1 6 0 0 … 1 1 0 2 7 0 0 … 1 1 8 0 0 … 0 0 0 4 … … … … 2 k - 1 1 1 … 1 1 1 CS 421 - Introduction to Algorithms k 46

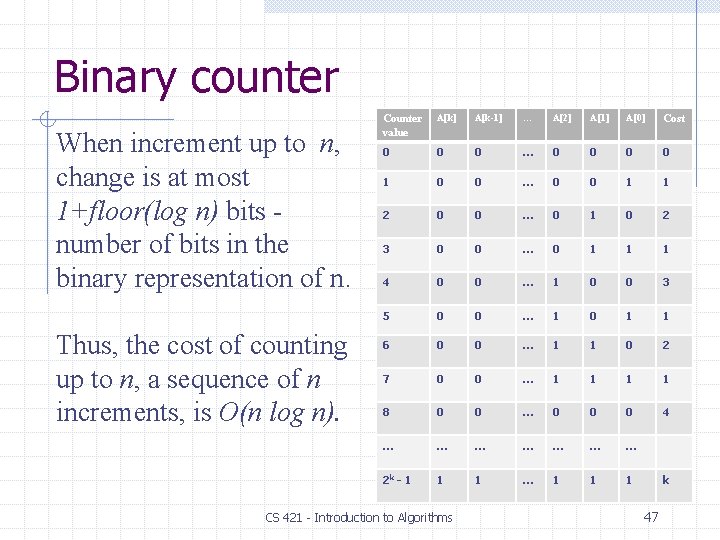
Binary counter When increment up to n, change is at most 1+floor(log n) bits number of bits in the binary representation of n. Thus, the cost of counting up to n, a sequence of n increments, is O(n log n). Counter value A[k] A[k-1] … A[2] A[1] A[0] Cost 0 0 0 … 0 0 1 1 2 0 0 … 0 1 0 2 3 0 0 … 0 1 1 1 4 0 0 … 1 0 0 3 5 0 0 … 1 0 1 1 6 0 0 … 1 1 0 2 7 0 0 … 1 1 8 0 0 … 0 0 0 4 … … … … 2 k - 1 1 1 … 1 1 1 CS 421 - Introduction to Algorithms k 47

Aggregate Method Aggregate method. Sum up sequence of operations, weighted by their cost. How often we flip each individual bit? Then sum those up to bound the total, rather than individually obtaining a worst case bound for each bit. How often is A[0] toggled in counting up to n? How often is A[1] toggled, A[2] toggled, etc? Every time, every other time, every fourth time, . . . CS 421 - Introduction to Algorithms 48

Aggregate Method CS 421 - Introduction to Algorithms 49

Aggregate Method k-1 ∞ j 0 CS 421 - Introduction to Algorithms 50

Accounting Method Recall. Each individual operation pays a certain amount to a central pot (ĉi – the amortized cost) • the actual cost of some operations is less than the amortized cost (ci < ĉi) and leaves a reserve for future operations. • some operations cost more than the amortized cost (ci > ĉi) and use the reserve in the central pot. The amount that each individual operation pays into the pot is set so that there is just enough to do all the work. CS 421 - Introduction to Algorithms 51

Accounting Method Binary Counter. For the binary counter, the only work is toggling a bit, so let cost be $1 (ci) to toggle a bit. What’s the amortized cost to pay for all the toggles as they occur? By the aggregate method, we found ĉi = 2, $2 would be a good guess (though not a guarantee). CS 421 - Introduction to Algorithms 52

Accounting Method What happens on an increment? • some m low-order bits (m ≥ 0) change from 1 to 0 • the m-th bit changes from 0 to 1. We pay $2 for flipping the m-th bit from 0 to 1 but only use $1, and leave at the m-th bit for later use. For the m bits changed from 1 to 0, we pay for those with the $1 left at those bits by previous operations. CS 421 - Introduction to Algorithms 53

Accounting Method Example. Assume a 6 -bit counter initialized to zero: A[5] A[4] A[3] A[2] A[1] A[0] 0 0 0 CS 421 - Introduction to Algorithms 54

Accounting Method Increment. Pay $1 to flip A[0] and save $1 at that location for future operations. A[5] A[4] A[3] A[2] A[1] A[0] 0 0 0 1 CS 421 - Introduction to Algorithms 55

Accounting Method Increment. Pay $1 to flip A[1] and save $1 at that location for future operations. Pay $1 from reserve for flipping A[0]. A[5] A[4] A[3] A[2] A[1] A[0] 0 0 1 0 CS 421 - Introduction to Algorithms 56

Accounting Method Increment. Pay $1 to flip A[0] and save $1 at that location for future operations. A[5] A[4] A[3] A[2] A[1] A[0] 0 0 1 1 CS 421 - Introduction to Algorithms 57

Accounting Method Increment. Pay $1 to flip A[2] and save $1 at that location for future operations. Pay $2 from reserve for flipping A[0] and A[1]. A[5] A[4] A[3] A[2] A[1] A[0] 0 0 0 1 0 0 CS 421 - Introduction to Algorithms 58

Accounting Method Increment. Pay $1 to flip A[0] and save $1 at that location for future operations. A[5] A[4] A[3] A[2] A[1] A[0] 0 0 0 1 CS 421 - Introduction to Algorithms 59

Accounting Method And so on… A[5] A[4] A[3] A[2] A[1] A[0] 0 0 0 1 CS 421 - Introduction to Algorithms 60

Accounting Method Theorem. Starting from the zero counter, a sequence of n increment operations flips O(n) bits. Proof. Because the algorithm maintain the invariant that every bit currently set to 1 has $1 credit that can used to flip back to 0. So the value of the credits at each bit is always ≥ 0. Thus, the amortized cost of the increment is 2, and the overall time is O(n) for n increments. . CS 421 - Introduction to Algorithms 61

Potential Method Potential Function. Let the potential Φ(Di) of the counter after the i-th operation be bi, the number of 1 s in the counter after the i-th operation. Φ(D 0) = 0 Φ(Di) ≥ 0 for all Di CS 421 - Introduction to Algorithms 62

Potential Method CS 421 - Introduction to Algorithms 63

Potential Method CS 421 - Introduction to Algorithms 64

Conclusions • Amortized costs can provide a clean abstraction of data-structure performance. • Any of the analysis methods can be used when an amortized analysis is called for, but each method has some situations where it is arguably the simplest or most precise. • Different schemes may work for assigning amortized costs in the accounting method, or potentials in the potential method, sometimes yielding radically different bounds. CS 421 - Introduction to Algorithms 65