Speeding Up Enumeration Algorithms with Amortized Analysis Takeaki

Speeding Up Enumeration Algorithms with Amortized Analysis Takeaki Uno (National Institute of Informatics, JAPAN)

Motivation & Goal • There have been proposed huge number of (output) polynomial time listing, enumeration, and generation algorithms <= Good construction schemes: Back tracking, Gray code, Binary partition, and Reverse search • But, there are relatively few studies on Speeding up those algorithms (reducing complexities)

Motivation & Goal (2) • Recently, enumeration algorithms are used in practical problems: data mining, bioinformatics, computational linguistics Practical & theoretical fast algorithms are required • However, reducing time complexity ( per output ) is not easy

Motivation & Goal (3) • Reducing # of iterations usually, hard ( or impossible if O(#output) ) • Reducing time complexity of iterations usually, difficult ( O(n 5) O(n 4) is possible, but O(n) O(log n), O(1) is hard ) Scheme using amortized analysis is required we propose a scheme with amortized analysis

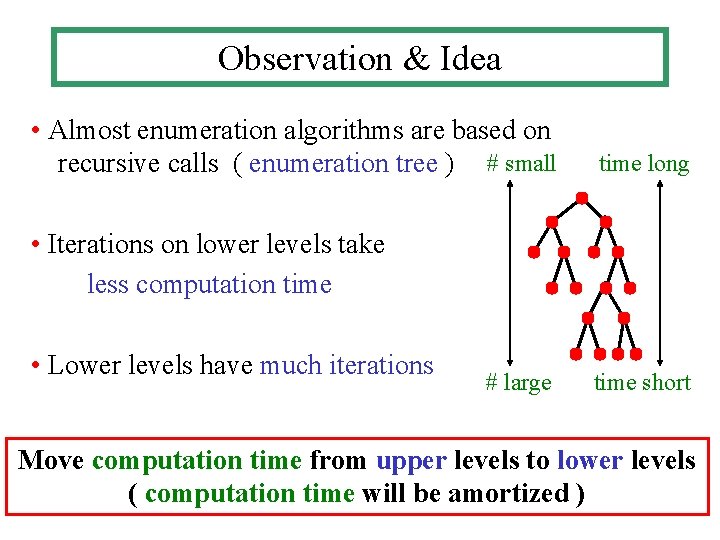
Observation & Idea • Almost enumeration algorithms are based on recursive calls ( enumeration tree ) # small time long • Iterations on lower levels take less computation time • Lower levels have much iterations # large time short Move computation time from upper levels to lower levels ( computation time will be amortized )

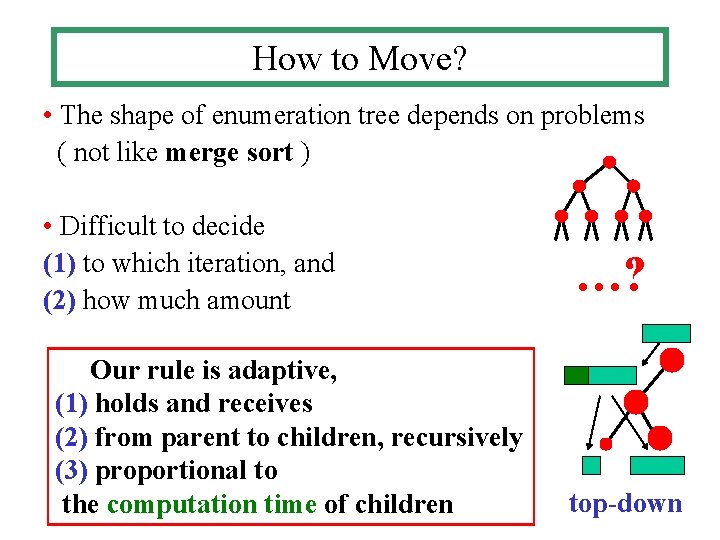
How to Move? • The shape of enumeration tree depends on problems ( not like merge sort ) • Difficult to decide (1) to which iteration, and (2) how much amount Our rule is adaptive, (1) holds and receives (2) from parent to children, recursively (3) proportional to the computation time of children …? top-down

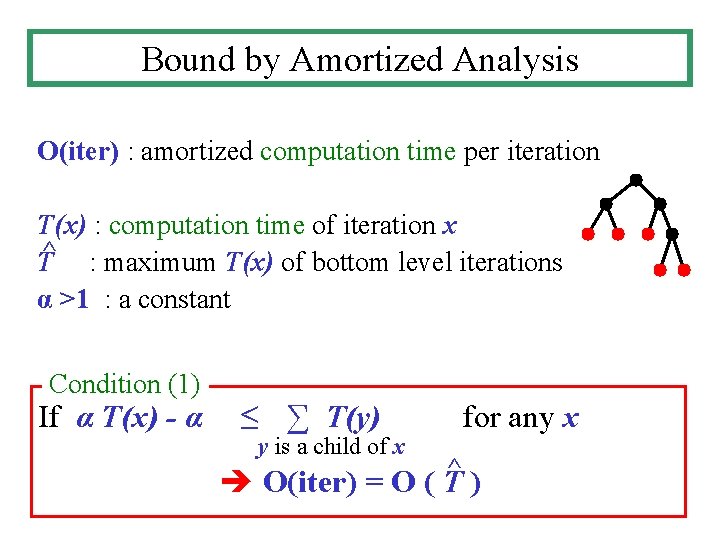
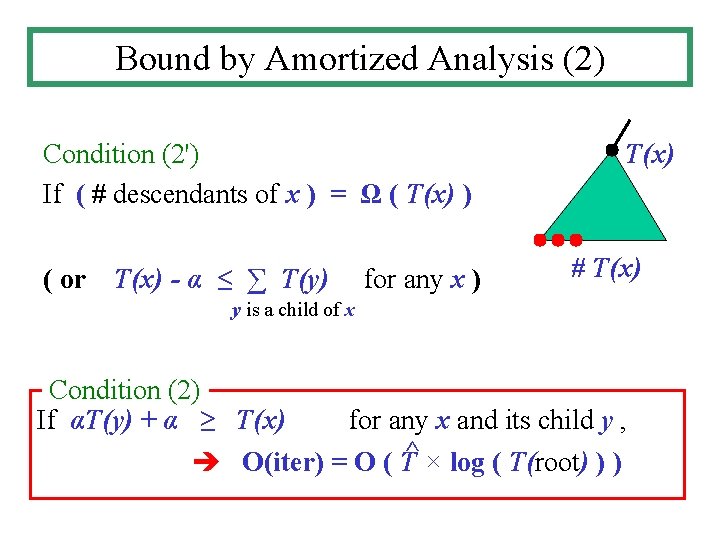
Bound by Amortized Analysis O(iter) : amortized computation time per iteration T(x) : computation time of iteration x T^ : maximum T(x) of bottom level iterations α >1 : a constant Condition (1) If α T(x) - α ≤ ∑ T(y) y is a child of x for any x ^ O(iter) = O ( T )

Condition (1) does not hold If several x do not hold Condition (1) : α T(x) - α ≤ ∑ T(y) Some iterations receive much computation time from parents If x receives > α T(x) move computation time to all descendants of x x

Bound by Amortized Analysis (2) Condition (2') If ( # descendants of x ) = Ω ( T(x) ) ( or T(x) - α ≤ ∑ T(y) for any x ) T(x) # T(x) y is a child of x Condition (2) If αT(y) + α ≥ T(x) for any x and its child y , O(iter) = O ( T^ × log ( T(root) ) )

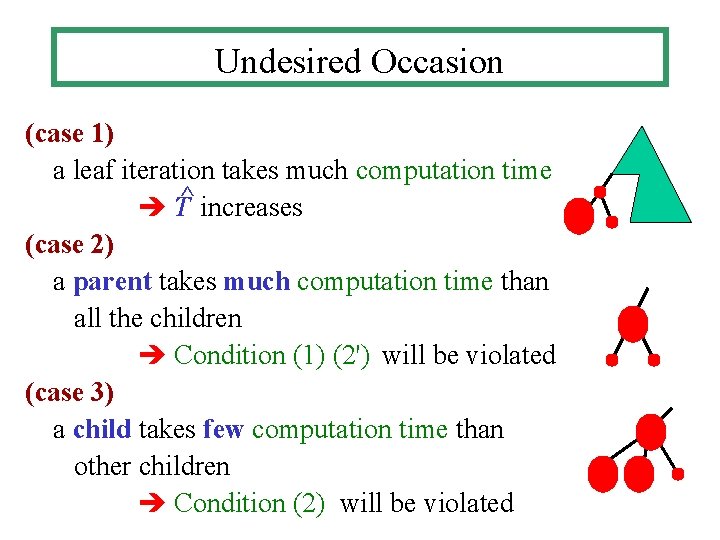
Undesired Occasion (case 1) a leaf iteration takes much computation time T^ increases (case 2) a parent takes much computation time than all the children Condition (1) (2') will be violated (case 3) a child takes few computation time than other children Condition (2) will be violated

Procedure to Avoid In each iteration, we do Trimming: remove unnecessary parts of input of each iteration for avoiding ( case 1 & 2 ) Balancing: take balance of computation time of children for avoiding ( case 3 )

Results ( previous best new ) Matchings Algorithm satisfying Condition (1) O(|V|) O( 1 ) Matroid Bases Algorithm satisfying Condition (1) m : #elements O(mn) O(1) ( oracle calls ) n : rank Directed spanning trees Trimming & balancing satisfying Condition (2') & (2) O( |V|1/2 ) O( log 2|V| ) Bipartite Perfect matchings Trimming & balancing satisfying Condition (2') & (2) O( |V| ) O( log|V| )

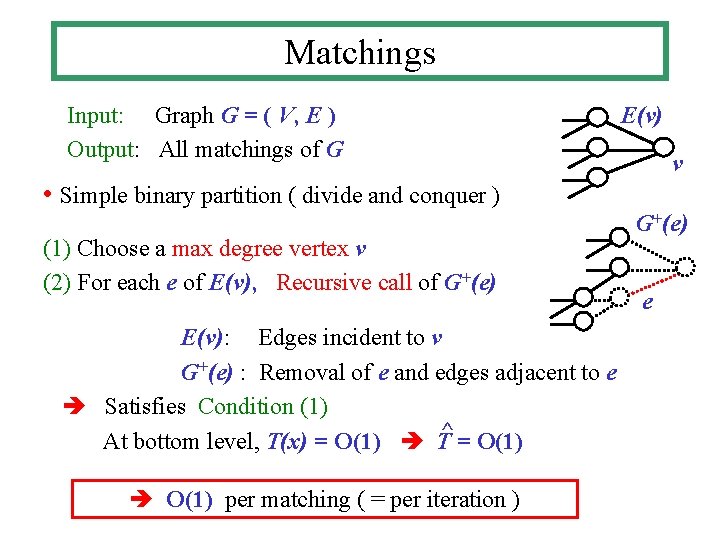
Matchings Input: Graph G = ( V, E ) Output: All matchings of G • Simple binary partition ( divide and conquer ) (1) Choose a max degree vertex v (2) For each e of E(v), Recursive call of G+(e) E(v): Edges incident to v G+(e) : Removal of e and edges adjacent to e Satisfies Condition (1) At bottom level, T(x) = O(1) T^ = O(1) per matching ( = per iteration ) E(v) v G+(e) e

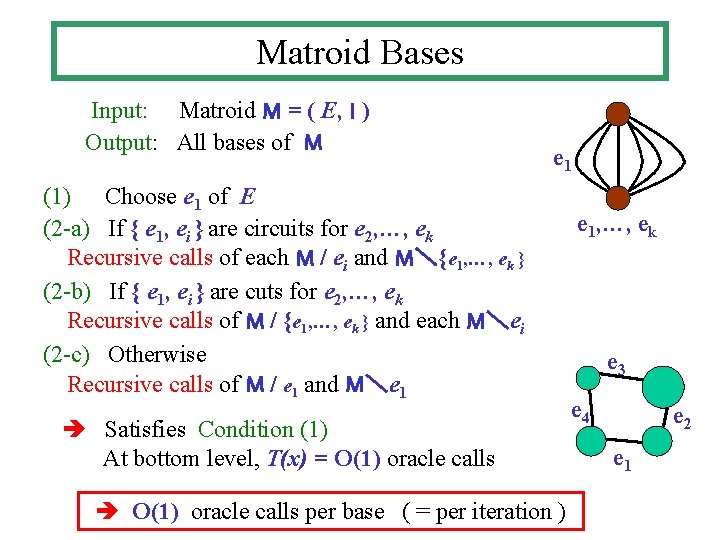
Matroid Bases Input: Matroid M = ( E, I ) Output: All bases of M e 1 (1) Choose e 1 of E (2 -a) If { e 1, ei } are circuits for e 2, …, ek Recursive calls of each M / ei and M＼{e 1, …, ek } (2 -b) If { e 1, ei } are cuts for e 2, …, ek Recursive calls of M / {e 1, …, ek } and each M＼ei (2 -c) Otherwise Recursive calls of M / e 1 and M＼e 1 Satisfies Condition (1) At bottom level, T(x) = O(1) oracle calls per base ( = per iteration ) e 1, …, ek e 3 e 4 e 2 e 1

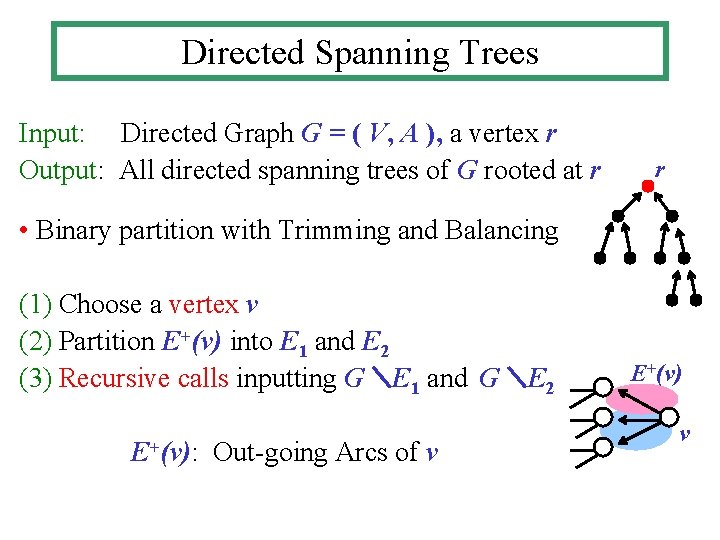
Directed Spanning Trees Input: Directed Graph G = ( V, A ), a vertex r Output: All directed spanning trees of G rooted at r r • Binary partition with Trimming and Balancing (1) Choose a vertex v (2) Partition E+(v) into E 1 and E 2 (3) Recursive calls inputting G＼E 1 and G＼E 2 E+(v): Out-going Arcs of v E+(v) v

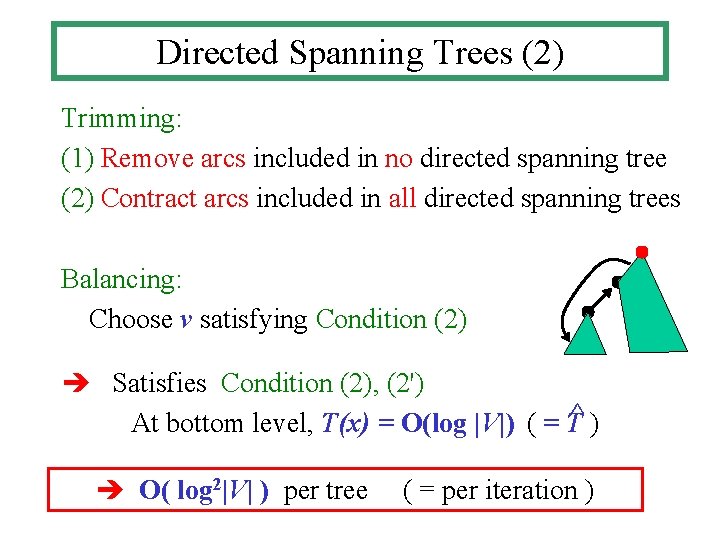
Directed Spanning Trees (2) Trimming: (1) Remove arcs included in no directed spanning tree (2) Contract arcs included in all directed spanning trees Balancing: Choose v satisfying Condition (2) Satisfies Condition (2), (2') ^) At bottom level, T(x) = O(log |V|) ( = T O( log 2|V| ) per tree ( = per iteration )

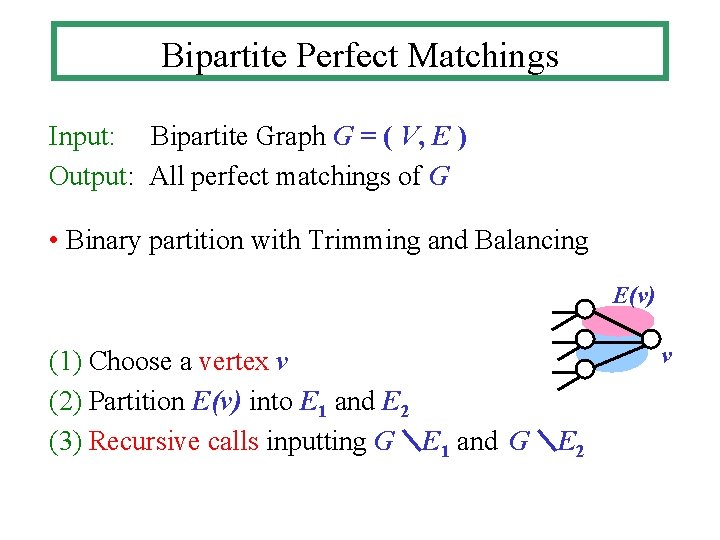
Bipartite Perfect Matchings Input: Bipartite Graph G = ( V, E ) Output: All perfect matchings of G • Binary partition with Trimming and Balancing E(v) (1) Choose a vertex v (2) Partition E(v) into E 1 and E 2 (3) Recursive calls inputting G＼E 1 and G＼E 2 v

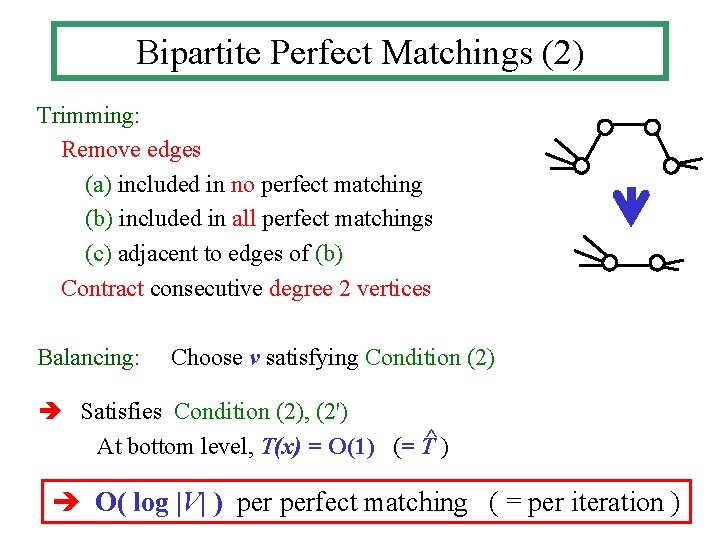
Bipartite Perfect Matchings (2) Trimming: Remove edges (a) included in no perfect matching (b) included in all perfect matchings (c) adjacent to edges of (b) Contract consecutive degree 2 vertices Balancing: Choose v satisfying Condition (2) Satisfies Condition (2), (2') At bottom level, T(x) = O(1) (= T^ ) O( log |V| ) perfect matching ( = per iteration )

Conclusion • Proposed a new amortized analysis • Proposed a new speeding up scheme ( trimming and balancing ) • Proposed fast enumeration algorithms for • mathings • matroid bases • directed spanning trees • bipartite perfect mathings

Future Works • Improve other algorithms • possible? undirected s-t paths minimal cuts of planer graphs directed paths of planer graphs • impossible? minimal cuts directed s-t paths stable sets