Informcielmlet Nagy Szilvia 8 Hammingkdok 2005 Szchenyi Informcielmlet

Információelmélet Nagy Szilvia 8. Hamming-kódok 2005.

Széchenyi Információelmélet – Hamming-kódok István Egyetem Hamming-kódok Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód A Hamming-kódok olyan perfekt kódok, amelyek egyszerű hibát képesek kijavítani. Megközelítés: adott n k paritásszegmenshosszhoz megtalálni a maximális k üzenethosszt, amelyre a kód egy hibát még tud javítani (azaz amelyre a kódtávolság még 2 -nél nem kisebb). 2

Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Bináris Hamming-kódok esetén mind a tömörített üzenet, mind a kódszavak csak 0 -kból és 1 -esekből állnak: b {0, 1}k, c {0, 1}n. A csatorna által a v-ben létrehozott (egyetlen) hiba csak 1 nagyságú lehet, csak a pozíciója kérdéses. 3

Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Legyen a paritásmátrix Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Egy hiba esetén Δc egyetlen 1 -est (és n k 1 db nullát) tartalmaz, ha az az egyetlen 1 -es az i-edik helyen van, 4

Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Írjuk egymás alá az összes lehetséges nem nulla szindrómát – az összes nem csupa nullából álló n k hosszúságú vektort: • Az így kapott HT paritásmátrixszal szorozzunk meg egy vektort, • A kapott szindrómát keressük meg HTben: ahányadik sorban az van, annyiadik helyen hibázott a csatorna. • Arra a helyre ellentétes bitet írunk, és a vektort kijavítottuk. 5

Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód HT oszlopainak száma n k, az összes lehetséges n k hosszú, 0 -kból és 1 -ekbők álló vektorok száma: Ebből egy tiszta nullából áll, így a HT sorainak száma: n=2 n k 1 Néhány összetartozó n és k érték: 2 3 4 5 6 7 3 7 15 31 63 127 k 1 4 11 26 57 120 6

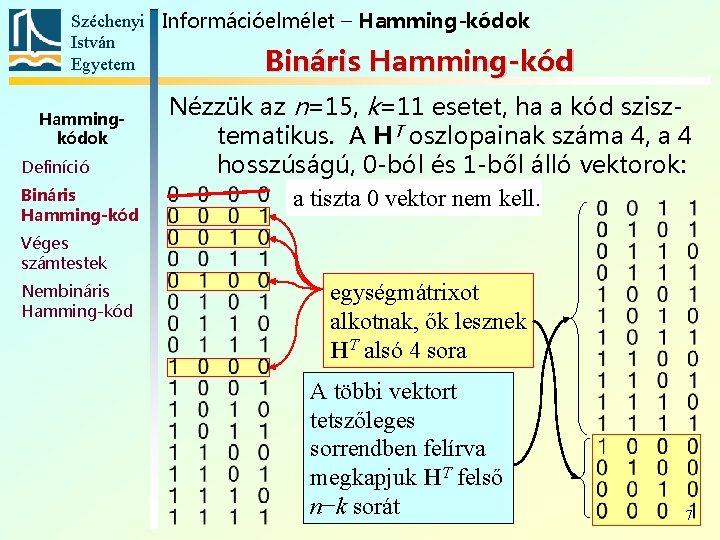
Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Nézzük az n=15, k=11 esetet, ha a kód szisztematikus. A HT oszlopainak száma 4, a 4 hosszúságú, 0 -ból és 1 -ből álló vektorok: a tiszta 0 vektor nem kell. Véges számtestek Nembináris Hamming-kód egységmátrixot alkotnak, ők lesznek HT alsó 4 sora A többi vektort tetszőleges sorrendben felírva megkapjuk HT felső n−k sorát 7

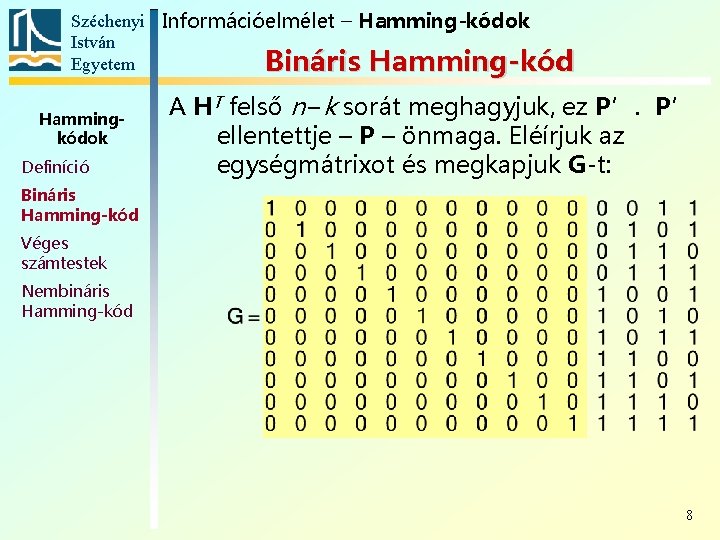
Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció A HT felső n−k sorát meghagyjuk, ez P’. P’ ellentettje – P – önmaga. Eléírjuk az egységmátrixot és megkapjuk G-t: Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód 8

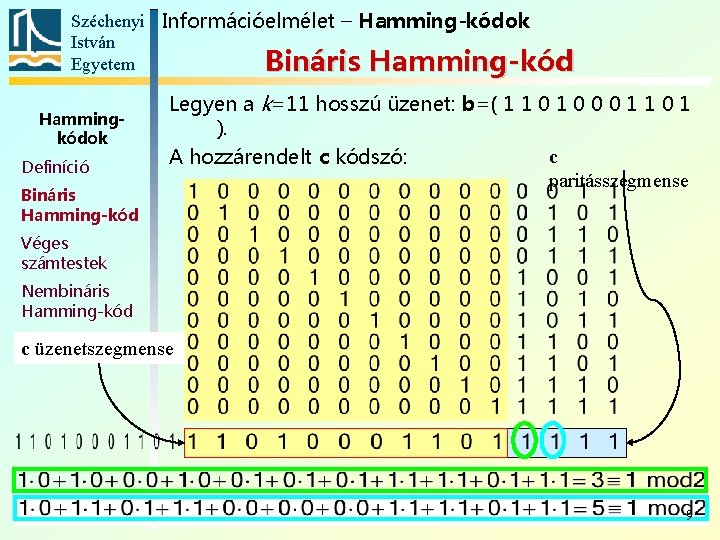
Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Legyen a k=11 hosszú üzenet: b=( 1 1 0 0 0 1 1 0 1 ). c A hozzárendelt c kódszó: paritásszegmense Véges számtestek Nembináris Hamming-kód c üzenetszegmense 9

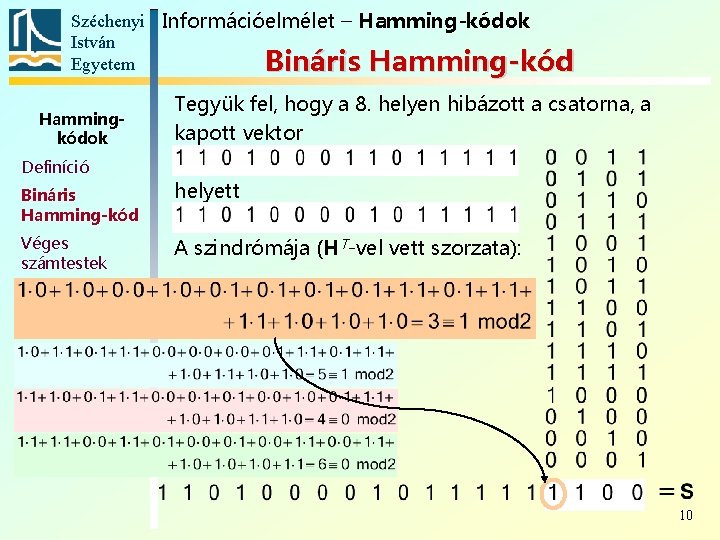
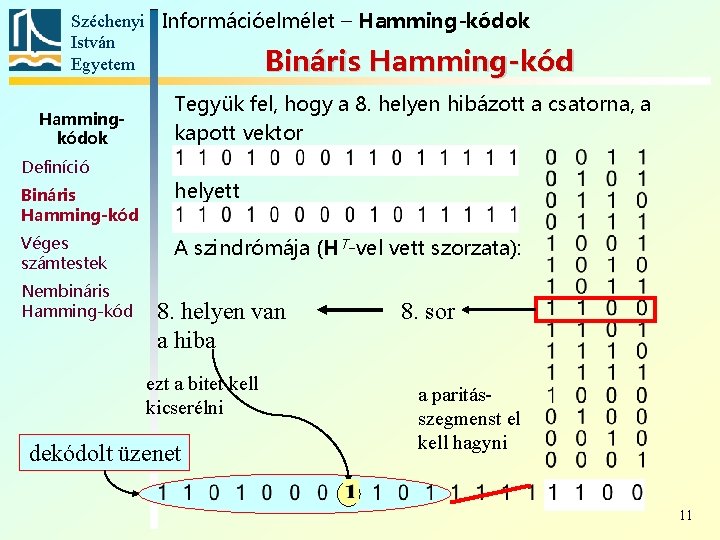
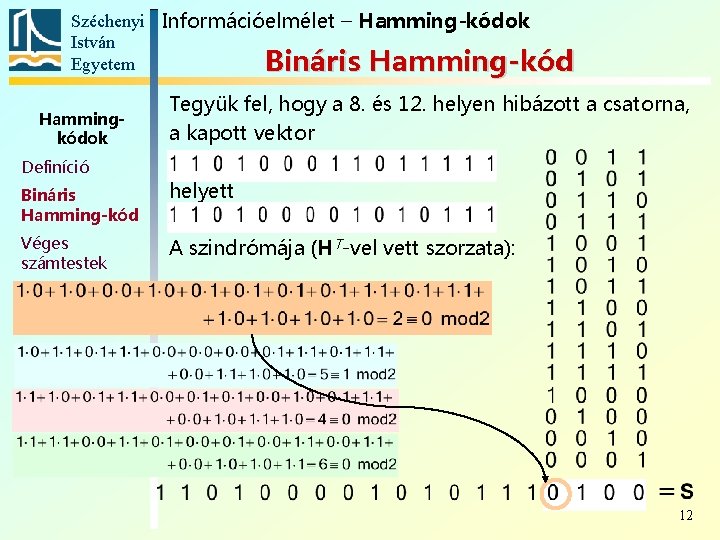
Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Tegyük fel, hogy a 8. helyen hibázott a csatorna, a kapott vektor Bináris Hamming-kód helyett Véges számtestek A szindrómája (HT-vel vett szorzata): Nembináris Hamming-kód 10

Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Tegyük fel, hogy a 8. helyen hibázott a csatorna, a kapott vektor Bináris Hamming-kód helyett Véges számtestek A szindrómája (HT-vel vett szorzata): Nembináris Hamming-kód 8. helyen van a hiba ezt a bitet kell kicserélni dekódolt üzenet 8. sor a paritásszegmenst el kell hagyni 11

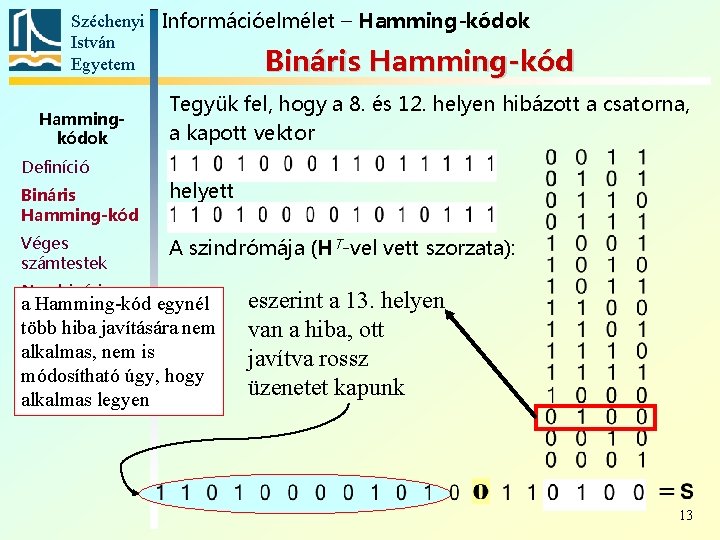
Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Tegyük fel, hogy a 8. és 12. helyen hibázott a csatorna, a kapott vektor Bináris Hamming-kód helyett Véges számtestek A szindrómája (HT-vel vett szorzata): Nembináris Hamming-kód 12

Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Tegyük fel, hogy a 8. és 12. helyen hibázott a csatorna, a kapott vektor Bináris Hamming-kód helyett Véges számtestek A szindrómája (HT-vel vett szorzata): Nembináris eszerint a 13. helyen van a hiba, ott javítva rossz üzenetet kapunk a. Hamming-kód egynél több hiba javítására nem alkalmas, nem is módosítható úgy, hogy alkalmas legyen 13

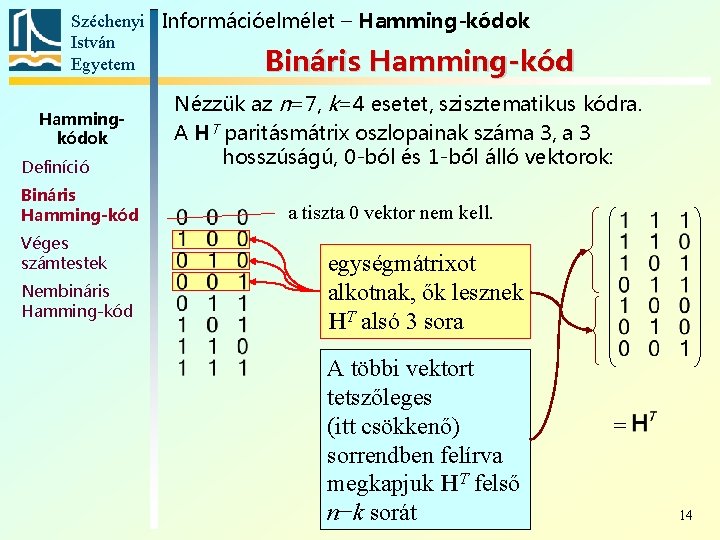
Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Nézzük az n=7, k=4 esetet, szisztematikus kódra. A HT paritásmátrix oszlopainak száma 3, a 3 hosszúságú, 0 -ból és 1 -ből álló vektorok: a tiszta 0 vektor nem kell. egységmátrixot alkotnak, ők lesznek HT alsó 3 sora A többi vektort tetszőleges (itt csökkenő) sorrendben felírva megkapjuk HT felső n−k sorát 14

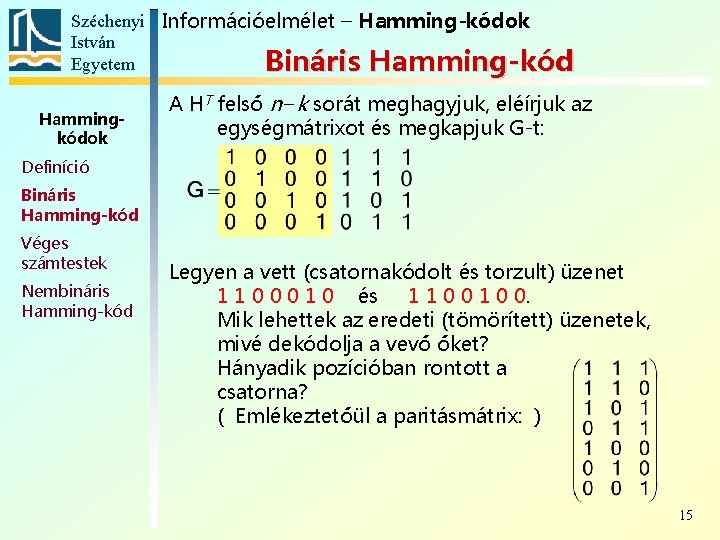
Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok A HT felső n−k sorát meghagyjuk, eléírjuk az egységmátrixot és megkapjuk G-t: Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Legyen a vett (csatornakódolt és torzult) üzenet 1 1 0 0 0 1 0 és 1 1 0 0. Mik lehettek az eredeti (tömörített) üzenetek, mivé dekódolja a vevő őket? Hányadik pozícióban rontott a csatorna? ( Emlékeztetőül a paritásmátrix: ) 15

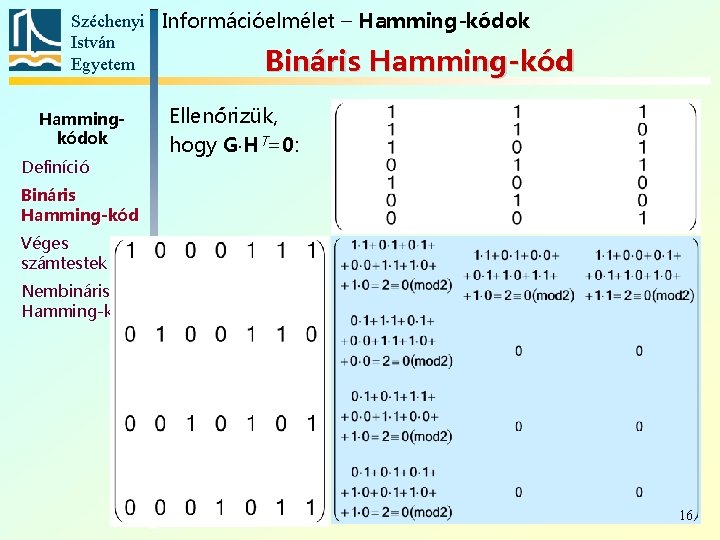
Széchenyi Információelmélet – Hamming-kódok István Egyetem Bináris Hamming-kód Hammingkódok Definíció Ellenőrizük, hogy G HT=0: Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód 16

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Egy számokból álló GF(N)={0, 1, …, N− 1} halmaz véges test, vagy Galois-test, ha értelmezve van a t és u V elemei között egy összeadás ( t + u GF(N) ) és egy szorzás ( t u GF(N) ) amelyekre: 1. ) a) t + u = u + t (az összeadás kommutatív) b) ha s GF(N), ( s + t )+ u = s + ( t + u ) (asszociatív) c) 0, melyre t GF(N): t+0=t d) t GF(N)-re −t , melyre t + (−t ) = 0 17

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Egy számokból álló GF(N)={0, 1, …, N− 1} halmaz véges test, vagy Galois-test, ha értelmezve van a t és u V elemei között egy összeadás ( t + u GF(N) ) és egy szorzás ( t u GF(N) ) amelyekre: 2. ) a) t u = u t (a szorzás kommutatív) b) ha s GF(N), ( s t ) u = s ( t u ) (asszociatív) c) 1, melyre t GF(N): t 1=t d) t GF(N)-re t − 1 , melyre t ( t − 1 ) = 1 18

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Egy számokból álló GF(N)={0, 1, …, N− 1} halmaz véges test, vagy Galois-test, ha értelmezve van a t és u V elemei között egy összeadás ( t + u GF(N) ) és egy szorzás ( t u GF(N) ) amelyekre: 3. ) a) ha s GF(N), s ( t + u ) = s t + s u (+ és disztributív) b) t GF(N): t 0 = 0. 19

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Példa: a {0, 1} halmaz a következő szorzó és összeadó táblával: + 0 1 0 0 0 1 1 0 1 Ez a hagyományos összeadás és szorzás azzal a kitétellel, hogy ha az eredmény kivezetne a halmazból, akkor a 2 -vel való osztás utáni maradékát vesszük. 20

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Legyen GF(5)={0, 1, 2, 3, 4} elemei között értelmezett összeadás és szorzás a szokásos számok közötti összeadás és Definíció szorzás azzal a megkötéssel, hogy ha az Bináris eredmény kivezetne a halmazból, akkor Hamming-kód annak 5 -tel való osztása utáni maradékát Véges vesszük eredménynek (moduló 5 számtestek összeadás és szorzás) Nembináris Hamming-kód 1. ) a) t + u = u + t Ezek teljesülése b) ha s GF(N), ( s + t )+ u = s + ( t + u ) egyértelmű: a modulo 5 c) 0, melyre t GF(N): t+0=t osztás és az d) t GF(N)-re −t , melyre összeadás t + (−t ) = 0 felcserélhető Hammingkódok a nullelem a 0 21

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód testekről 1. ) d) t GF(N)-re −t , melyre t + (−t ) = 0 nem véges testek esetén egy szám ellentettje negatív lenne. Vegyük ennek 5 -tel való osztása után keletkező maradékot, ez lesz a szám ellentettje: szám ellentett 0 0 1 2 3 4 5− 1= 5− 2= 5− 3= 5− 4= 4 3 2 1 22

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Legyen GF(5)={0, 1, 2, 3, 4} elemei között értelmezett összeadás és szorzás a szokásos számok közötti összeadás és Definíció szorzás azzal a megkötéssel, hogy ha az Bináris eredmény kivezetne a halmazból, akkor Hamming-kód annak 5 -tel való osztása utáni maradékát Véges vesszük eredménynek (moduló 5 számtestek összeadás és szorzás) Nembináris Hamming-kód 2. ) a) t u = u t Ezek teljesülése b) ha s GF(N), ( s t ) u = s ( t u ) egyértelmű: a modulo 5 c) 1, melyre t GF(N): t 1=t osztás és a − 1 , melyre d) t GF ( N )-re t szorzás − 1 ) = 1 t ( t felcserélhető Hammingkódok az egységelem az 1 23

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem Hammingkódok 2. ) testekről d) t GF(N)-re t − 1 , melyre Definíció t ( t − 1 ) = 1 Bináris nem véges testek esetén egy szám inverze Hamming-kód tört lenne. Az 5 prímszám, sem 2, sem 3, Véges sem pedig 4 nem osztója, ha ezek közül számtestek kettőt összeszorzunk, nem kaphatunk 0 Nembináris Hamming-kód maradékot. A szorzótáblájuk: 2 3 4 2 2 2=4≡ 4 mod 5 2 3=6≡ 1 mod 5 2 4=8≡ 3 mod 5 3 3 2=6≡ 1 mod 5 3 3=9≡ 4 mod 5 3 4=12≡ 2 mod 5 4 4 2=8≡ 3 mod 5 4 3=12≡ 2 mod 5 4 4=16≡ 1 mod 5 2 inverze 3, 3 -é 2, 4 -é pedig önmaga. (1 24 inverze eleve önmaga)

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem Hammingkódok 2. ) testekről d) t GF(N)-re t − 1 , melyre Definíció t ( t − 1 ) = 1 Bináris nem véges testek esetén egy szám inverze Hamming-kód tört lenne. Az 5 prímszám, sem 2, sem 3, Véges sem pedig 4 nem osztója, ha ezek közül számtestek kettőt összeszorzunk, nem kaphatunk 0 Nembináris Hamming-kód maradékot. A szorzótáblájuk: 2 3 4 2 2 2=4≡ 4 mod 5 2 3=6≡ 1 mod 5 2 4=8≡ 3 mod 5 3 3 2=6≡ 1 mod 5 3 3=9≡ 4 mod 5 3 4=12≡ 2 mod 5 4 4 2=8≡ 3 mod 5 4 3=12≡ 2 mod 5 4 4=16≡ 1 mod 5 Egy t szám inverze a GF(5) véges testen belül az az elem amellyel összeszorozva az eredmény 5 -tel osztva 1 maradékot ad. 25

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Legyen GF(5)={0, 1, 2, 3, 4} elemei között értelmezett összeadás és szorzás a szokásos számok közötti összeadás és szorzás azzal a megkötéssel, hogy ha az eredmény kivezetne a halmazból, akkor annak 5 -tel való osztása utáni maradékát vesszük eredménynek (moduló 5 összeadás és szorzás) 3. ) a) ha s GF(N), s ( t + u ) = s t + s u b) t GF(N): t 0 = 0. Ez a két feltétel is teljesül. Például: 3 (2+1)=9≡ 4 mod 5 3 2+3 1=9≡ 4 mod 5 26

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Az iménti eljárás általánosítható tetszőleges N prímszámra: Legyen GF(N)={0, 1, …, N− 1} elemei között értelmezett összeadás és szorzás a szokásos számok közötti összeadás és szorzás azzal a megkötéssel, hogy ha az eredmény kivezetne a halmazból, akkor annak N-nel való osztása utáni maradékát vesszük eredménynek (moduló N összeadás és szorzás). A véges számtest feltételei közül az ellentett és az inverz létezését kivéve mindegyik triviálisan teljesül. 27

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Inverz és ellentett elemet az 5 -ös esethez hasonlóan: • −t = N − t • A t − 1: t GF(N)={t 0 + t 1 + t 2 + …+ +t (N − 1)} számok mindegyike más és más, így közülük az egyik biztosan 1 (az t inverze, amelyikkel összeszorozva az 1 -et adja). Indoklás: Legyen s ≠ u , s, u GF(N). Ha t s = t u , akkor így s −u = 0, ami ellentmond a kezdőfeltételnek. (vagy t=0, de az nem érdekes) 28

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Egy t GF(N) elem hatványait is lehet értelmezni, mint önmagával vett szorzatait: Rekurzív definícióval t n-edik hatványa: • adott t 1=t • amíg i < n • t i + 1 = t i t. 29

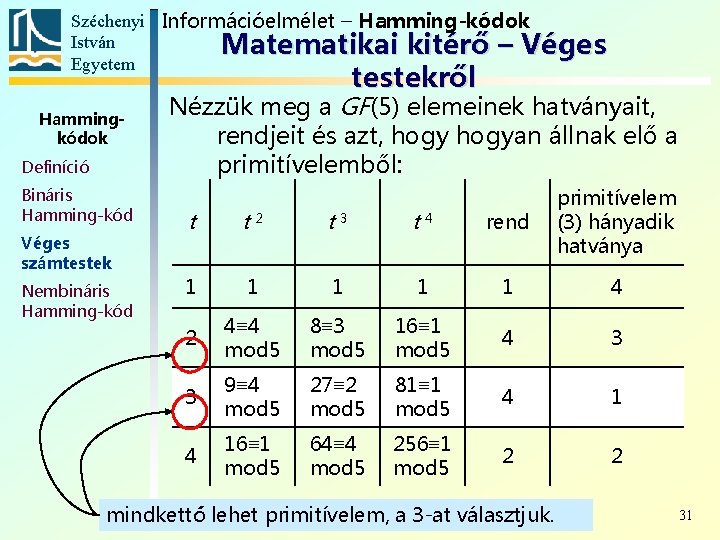
Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok A t GF(N) elem rendje Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Az 1 rendje 1, a 0 -nak nincs rendje. Az a t GF(N) elem, amelyre t első N− 1 hatványa mind különböző a véges test primitíveleme. Minden s GF(N) előáll a primitívelem hatványaként. 30

Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Nézzük meg a GF(5) elemeinek hatványait, rendjeit és azt, hogyan állnak elő a primitívelemből: t t 2 t 3 t 4 rend primitívelem (3) hányadik hatványa 1 1 1 4 2 4≡ 4 mod 5 8≡ 3 mod 5 16≡ 1 mod 5 4 3 3 9≡ 4 mod 5 27≡ 2 mod 5 81≡ 1 mod 5 4 16≡ 1 mod 5 64≡ 4 mod 5 256≡ 1 mod 5 2 2 mindkettő lehet primitívelem, a 3 -at választjuk. 31

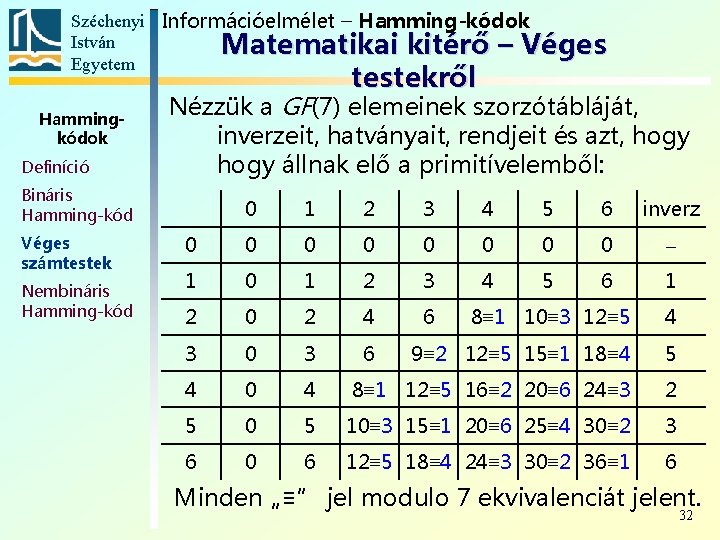
Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Nézzük a GF(7) elemeinek szorzótábláját, inverzeit, hatványait, rendjeit és azt, hogy állnak elő a primitívelemből: Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód 0 1 2 3 4 5 6 inverz 0 0 0 0 1 0 1 2 3 4 5 6 1 2 0 2 4 6 3 0 3 6 4 0 5 6 8≡ 1 10≡ 3 12≡ 5 4 9≡ 2 12≡ 5 15≡ 1 18≡ 4 5 4 8≡ 1 12≡ 5 16≡ 2 20≡ 6 24≡ 3 2 0 5 10≡ 3 15≡ 1 20≡ 6 25≡ 4 30≡ 2 3 0 6 12≡ 5 18≡ 4 24≡ 3 30≡ 2 36≡ 1 6 Minden „≡” jel modulo 7 ekvivalenciát jelent. 32

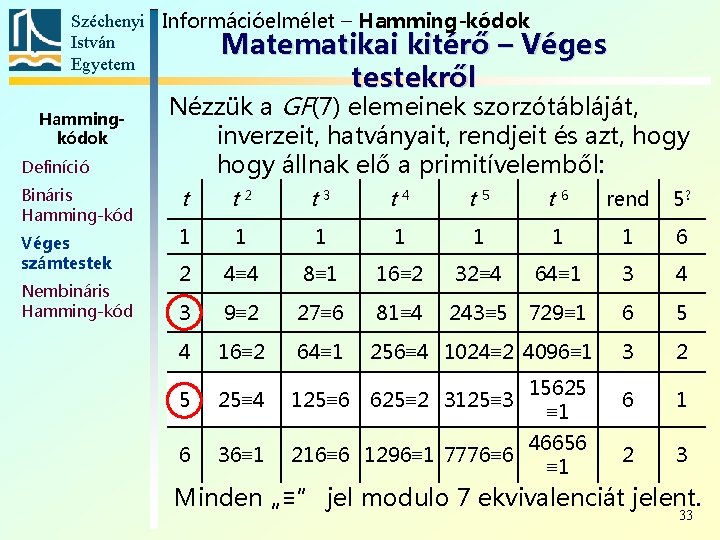
Széchenyi Információelmélet – Hamming-kódok István Matematikai kitérő – Véges Egyetem testekről Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Nézzük a GF(7) elemeinek szorzótábláját, inverzeit, hatványait, rendjeit és azt, hogy állnak elő a primitívelemből: t t 2 t 3 t 4 t 5 t 6 rend 5? 1 1 1 1 6 2 4≡ 4 8≡ 1 16≡ 2 32≡ 4 64≡ 1 3 4 3 9≡ 2 27≡ 6 81≡ 4 243≡ 5 729≡ 1 6 5 4 16≡ 2 64≡ 1 256≡ 4 1024≡ 2 4096≡ 1 3 2 5 25≡ 4 125≡ 6 625≡ 2 3125≡ 3 15625 ≡ 1 6 36≡ 1 216≡ 6 1296≡ 1 7776≡ 6 46656 ≡ 1 2 3 Minden „≡” jel modulo 7 ekvivalenciát jelent. 33

Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kódok esetén mind a tömörített üzenet, mind a kódszavak csak 0 -n és 1 -esen kívül más egész számokat is tartalmaznak: b {0, 1, …, N 1}k, c {0, 1, …, N 1}n, ahol N prím. A csatorna által a v-ben létrehozott (egyetlen) hiba nem csak 1 nagyságú lehet, így a pozícióján kívül a nagyságát is ki kell találni. Írjuk fel a paritásmátrixot itt is alakban. 34

Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Egyetlen hiba esetén a Δc hibavektor egyetlen nem nulla elemet (és n k 1 db nullát) tartalmaz. Legyen a hiba nagysága Δc, és legyen az i-edik pozícióban. Ekkor a szindróma: Ha HT sorainak – hi-knek – első nem nulla eleme 1, akkor a szindróma első nem nulla eleme pont Δc lesz. Írjuk egymás alá az összes lehetséges olyan nem nulla, n k hosszúságú vektort, amelynek az első nem nulla eleme 1: 35

Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Írjuk egymás alá az összes lehetséges olyan nem nulla, n k hosszúságú vektort, amelynek az első nem nulla eleme 1: ha az így kapott HT paritásmátrixszal szorzunk meg egy vektort, a kapott szindróma első nem nulla eleme lesz a hiba nagysága (Δc). A szindrómát a hiba nagyságával elosztva kapott új vektort (s/Δc) megkeressük HTben, ahányadik sorban az van, annyiadik helyen hibázott a csatorna. Azon a helyen a kapott hibanagysággal (Δcvel) korrigálunk, és a vektort kijavítottuk. 36

Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Az összes lehetséges olyan nem nulla, n k hosszúságú vektort, amelynek az első nem nulla eleme 1 száma, azaz az n kódszóhossz: a nem csupa nulla n k hosszú vektorok száma Véges számtestek Nembináris Hamming-kód Átrendezve: az első nem nulla elem N 1 féle lehet, ebből nekünk egy felel meg (az 1 -es) 37

Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód A gömbpakolási korlát (Hamming-korlát) n =1 hibára (r=N): Véges számtestek Nembináris Hamming-kód a Hammingkódok perfekt kódok 38

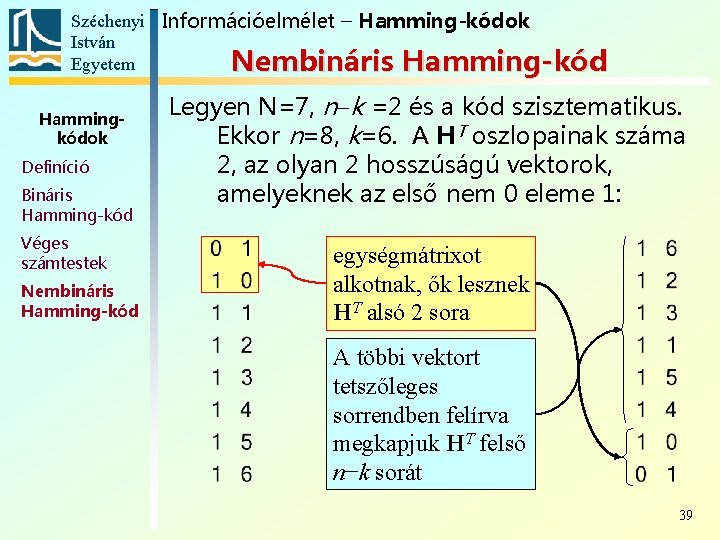
Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Legyen N=7, n k =2 és a kód szisztematikus. Ekkor n=8, k=6. A HT oszlopainak száma 2, az olyan 2 hosszúságú vektorok, amelyeknek az első nem 0 eleme 1: egységmátrixot alkotnak, ők lesznek HT alsó 2 sora A többi vektort tetszőleges sorrendben felírva megkapjuk HT felső n−k sorát 39

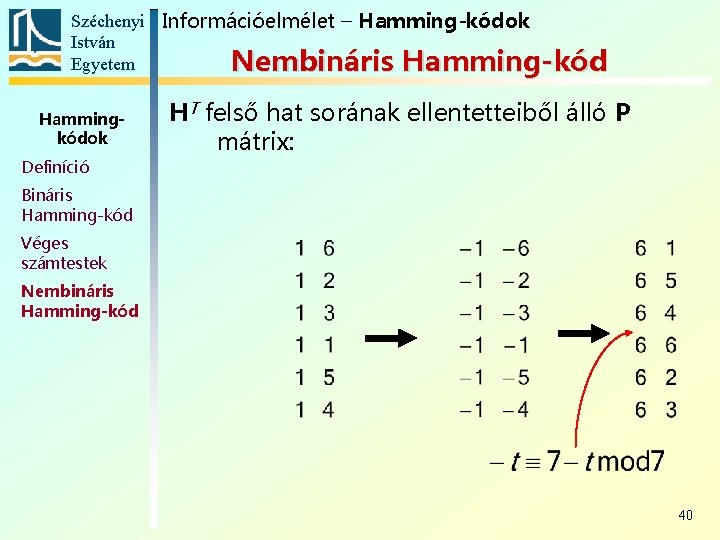
Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció HT felső hat sorának ellentetteiből álló P mátrix: Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód 40

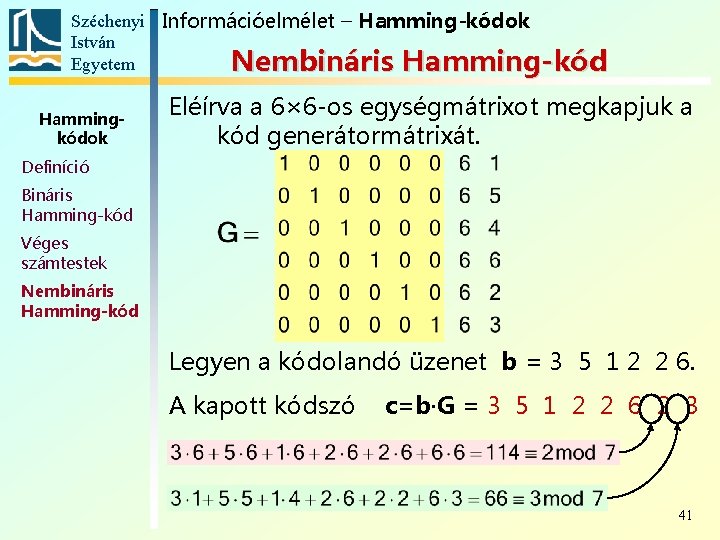
Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Eléírva a 6× 6 -os egységmátrixot megkapjuk a kód generátormátrixát. Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Legyen a kódolandó üzenet b = 3 5 1 2 2 6. A kapott kódszó c=b∙G = 3 5 1 2 2 6 2 3 41

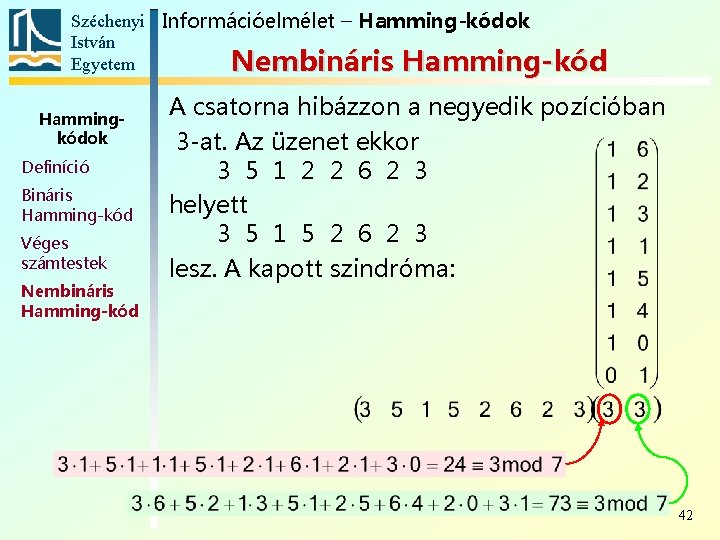
Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód A csatorna hibázzon a negyedik pozícióban 3 -at. Az üzenet ekkor 3 5 1 2 2 6 2 3 helyett 3 5 1 5 2 6 2 3 lesz. A kapott szindróma: 42

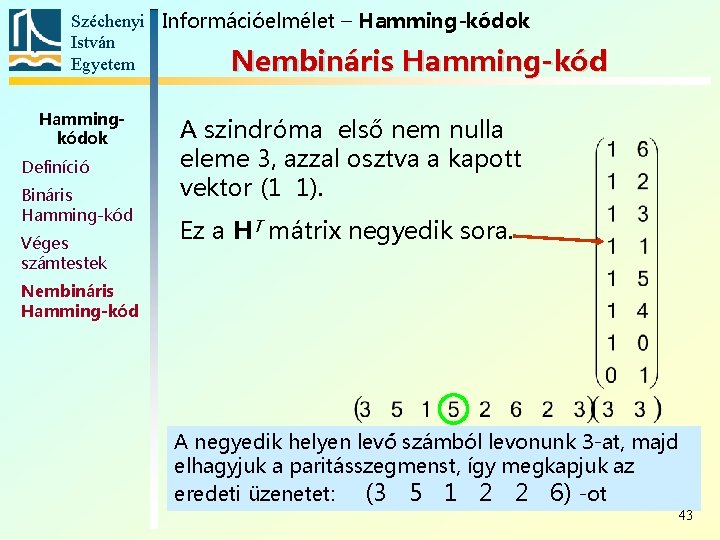
Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek A szindróma első nem nulla eleme 3, azzal osztva a kapott vektor (1 1). Ez a HT mátrix negyedik sora. Nembináris Hamming-kód A negyedik helyen levő számból levonunk 3 -at, majd elhagyjuk a paritásszegmenst, így megkapjuk az eredeti üzenetet: (3 5 1 2 2 6) -ot 43

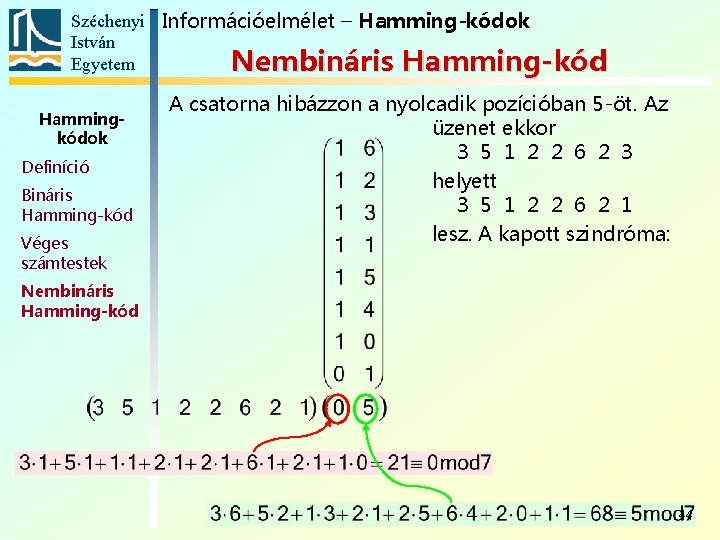
Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek A csatorna hibázzon a nyolcadik pozícióban 5 -öt. Az üzenet ekkor 3 5 1 2 2 6 2 3 helyett 3 5 1 2 2 6 2 1 lesz. A kapott szindróma: Nembináris Hamming-kód 44

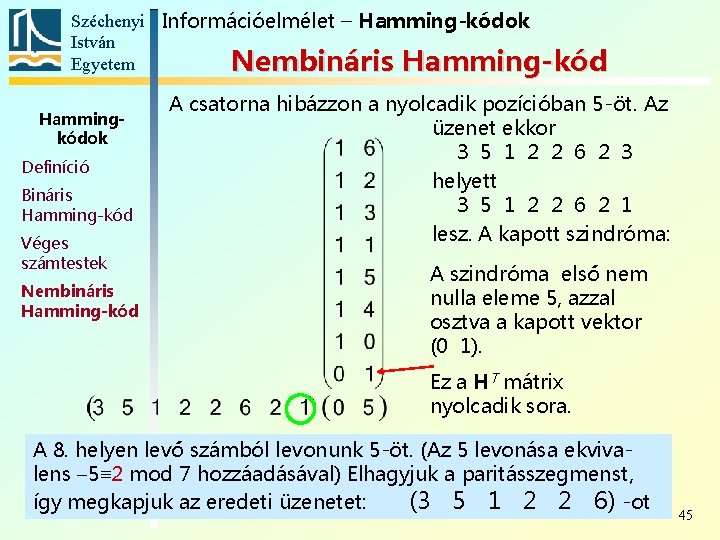
Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód A csatorna hibázzon a nyolcadik pozícióban 5 -öt. Az üzenet ekkor 3 5 1 2 2 6 2 3 helyett 3 5 1 2 2 6 2 1 lesz. A kapott szindróma: A szindróma első nem nulla eleme 5, azzal osztva a kapott vektor (0 1). Ez a HT mátrix nyolcadik sora. A 8. helyen levő számból levonunk 5 -öt. (Az 5 levonása ekvivalens 5≡ 2 mod 7 hozzáadásával) Elhagyjuk a paritásszegmenst, így megkapjuk az eredeti üzenetet: (3 5 1 2 2 6) -ot 45

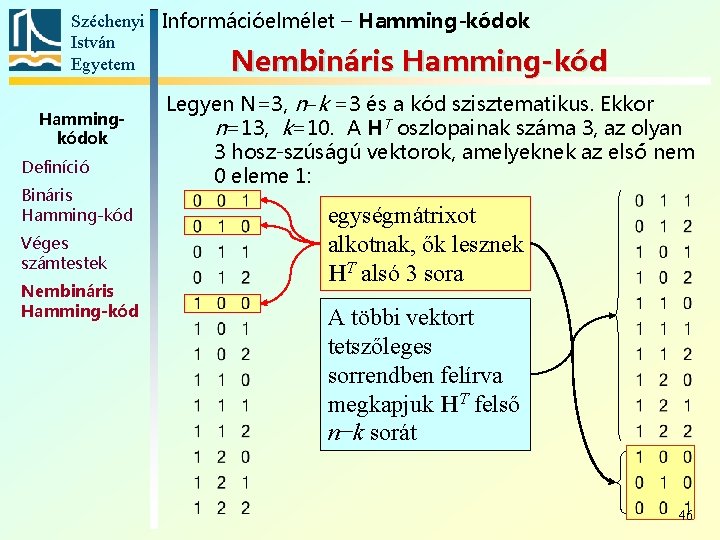
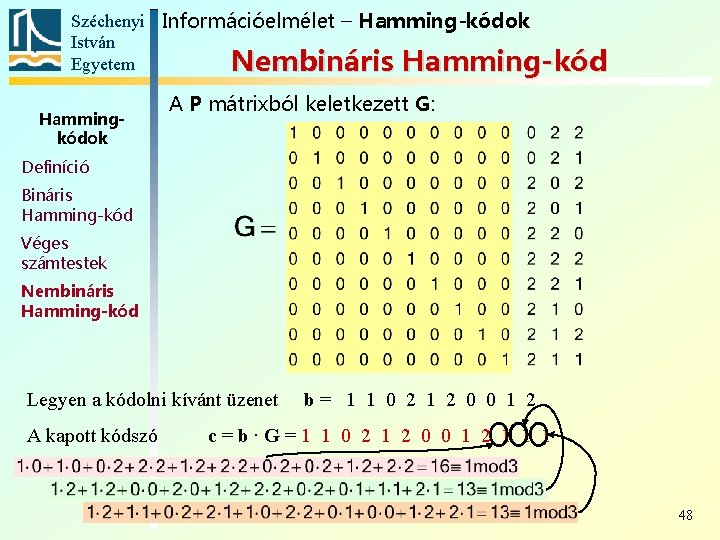
Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Legyen N=3, n k =3 és a kód szisztematikus. Ekkor n=13, k=10. A HT oszlopainak száma 3, az olyan 3 hosz-szúságú vektorok, amelyeknek az első nem 0 eleme 1: egységmátrixot alkotnak, ők lesznek HT alsó 3 sora A többi vektort tetszőleges sorrendben felírva megkapjuk HT felső n−k sorát 46

Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok HT felső hat sorának ellentetteiből álló P mátrix: Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód 47

Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok A P mátrixból keletkezett G: Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód Legyen a kódolni kívánt üzenet A kapott kódszó b= 1 1 0 2 1 2 0 0 1 2. c=b∙G=1 1 0 2 1 2 0 0 1 2 1 1 1 48

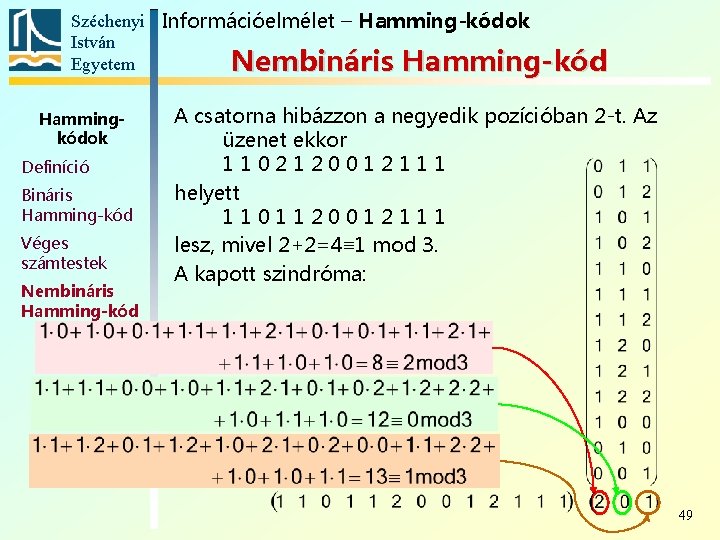
Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód A csatorna hibázzon a negyedik pozícióban 2 -t. Az üzenet ekkor 1102120012111 helyett 1101120012111 lesz, mivel 2+2=4≡ 1 mod 3. A kapott szindróma: 49

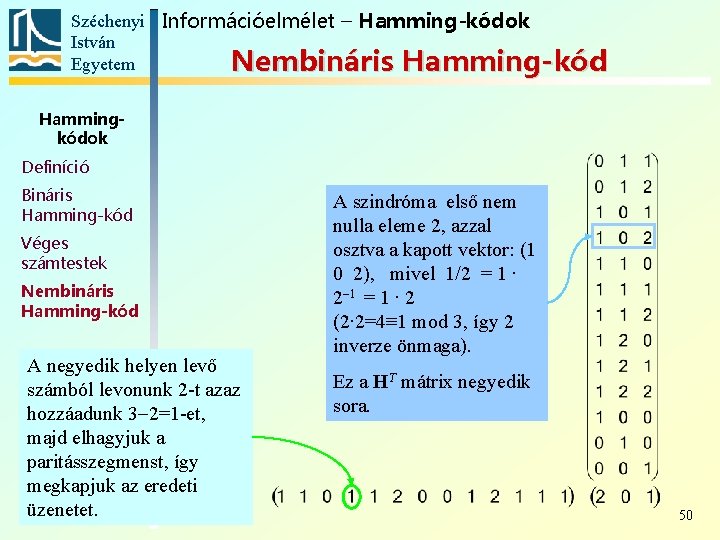
Széchenyi Információelmélet – Hamming-kódok István Egyetem Nembináris Hamming-kód Hammingkódok Definíció Bináris Hamming-kód Véges számtestek Nembináris Hamming-kód A negyedik helyen levő számból levonunk 2 -t azaz hozzáadunk 3 2=1 -et, majd elhagyjuk a paritásszegmenst, így megkapjuk az eredeti üzenetet. A szindróma első nem nulla eleme 2, azzal osztva a kapott vektor: (1 0 2), mivel 1/2 = 1 ∙ 2 1 = 1 ∙ 2 (2∙ 2=4≡ 1 mod 3, így 2 inverze önmaga). Ez a HT mátrix negyedik sora. 50