Informcielmlet Nagy Szilvia 10 ReedSolomonkdok 2005 Szchenyi Informcielmlet

Információelmélet Nagy Szilvia 10. Reed—Solomon-kódok 2005.

Széchenyi Információelmélet – Reed—Solomon-kódok István Generálóelemek Egyetem Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Legyen t 0 , t 1 , t 2 , …, tn− 1 a GF(N) véges test n darab különböző eleme, n<N. A Reed—Solomon-kódok a b=(b 0 , b 1 , …, b k− 1 ) üzenethez azt a c=(c 0 , c 1 , …, c n− 1 ) kódszót rendelik hozzá, amelynek a c i komponensei a Generátorpolinom Paritásellenőrzés GF(NM) számtestek formula szerint állnak elő. A t i generálóelemek kiválasztása határozza meg a kódot. 2

Széchenyi Információelmélet – Reed—Solomon-kódok István Generálóelemek Egyetem A kód generátormátrixa: Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek Ha ezzel a mátrixszal állítjuk elő a kódszót a b=(b 0 , b 1 , …, b k− 1 ) üzenetből, annak i-edik komponense: ami valóban b(ti). 3

Széchenyi Információelmélet – Reed—Solomon-kódok István Generálóelemek Egyetem Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Példa: Legyen t i=2 GF(5), b=(3, 1, 0, 2), a kapott c=(c 0, c 1, …, c n− 1 ) kódszó c i komponense ugyanez a generátormátrix i-edik oszlopával: Generátorpolinom Paritásellenőrzés GF(NM) számtestek 4

Széchenyi Információelmélet – Reed—Solomon-kódok István Egyetem Maximális távolság Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés Egy (n, k ) paraméterű Reed—Solomon-kód kódtávolsága dmin=n−k+1, azaz a kódra a Singleton-korlátban egyenlőség teljesül, tehát a Reed—Solomon-kódok maximális távolságúak (MDS-ek). Bizonyítás: Lineáris kódoknál a csupa nullából álló n hosszúságú vektor is a K halmaz eleme (kódszó), bármely c K vektornak ettől a vektortól vett eltérése a c súlya: GF(NM) számtestek 5

Széchenyi Információelmélet – Reed—Solomon-kódok István Egyetem Maximális távolság Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek c komponensei b(t i ) polinom-alakban állnak elő. A b(t ) polinom csak a gyökeire ad nulla eredményt. Mivel t i ≠ t j , egy gyök c-ben nem szerepelhet kétszer, a c nulla komponenseinek a száma tehát nem nagyobb, mint a b(t ) polinom gyökeinek a száma. A b(t ) k− 1 -edfokú polinom legfeljebb k− 1 gyökkel rendelkezik, így 6

Széchenyi Információelmélet – Reed—Solomon-kódok István Egyetem Maximális távolság Reed— Solomon-kódok Generáló elemek A kódtávolság – minimális súly: ugyanakkor a Singleton-korlát: Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek E két eredményt összevetve az állítást beláttuk. Ha dmin=n−k+1, akkor a kód legfeljebb n−k hibát tud jelezni, n−k törléses és (n−k )/2 egyszerű hibát tud javítani. 7

Széchenyi Információelmélet – Reed—Solomon-kódok István Egyetlen generálóelem Egyetem Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Legyen GF(N) rendje legalább n. ( ≠ 0) Ekkor -nak a 0 -diktól az n− 1 -edikig terjedő hatványai mind különbözőek lesznek, ezek lehetnek a Reed—Solomon-kódot létrehozó t i GF(N) véges testbeli elemek: A generátormátrix ezekkel: Paritásellenőrzés GF(NM) számtestek 8

Széchenyi Információelmélet – Reed—Solomon-kódok István Egyetlen generálóelem Egyetem Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom A GF(N) generáló elemmel definiált Reed— Solomon-kód a b=(b 0 , b 1 , …, b k− 1 ) üzenethez azt a c=(c 0 , c 1 , …, c n− 1 ) kódszót rendeli hozzá, amelynek a c i komponensei: avagy Paritásellenőrzés GF(NM) számtestek 9

Széchenyi Információelmélet – Reed—Solomon-kódok István Egyetlen generálóelem Egyetem A c kódszóhoz, melynek komponensei: Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek a ciklikus kódoknál megszokott módon polinomokat lehet rendelni: Generátorpolinom Paritásellenőrzés GF(NM) számtestek ami c i kifejezését beírva: alakú lesz. 10

Széchenyi Információelmélet – Reed—Solomon-kódok István Paritásegyenletek Egyetem Reed— Solomon-kódok Generáló elemek Helyettesítsünk be a ℓ GF(N) elemeket ℓ = 0, 1, …, n k -ra a Reed—Solomon-kód egyes kódszavaihoz rendelt polinomokba: Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek Mivel 0 < ℓ ≤ n k , és 0 ≤ j ≤ k 1, 0 < j + ℓ ≤ n 1. Mivel legalább n-edrendű elem GF(N)-ben, Így a mértani sor összegképlete szerint: 11

Széchenyi Információelmélet – Reed—Solomon-kódok István Paritásegyenletek Egyetem Reed— Solomon-kódok Generáló elemek Generálóelem A mértani sor összegképlete szerint: Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek mivel n =1, a számláló 0, így c( ℓ ) = 0, ℓ = 1, …, n k -ra. Ezek a Reed—Solomon-kód paritásegyenletei. 12

Széchenyi Információelmélet – Reed—Solomon-kódok István Paritásegyenletek Egyetem Reed— Solomon-kódok A c ( ℓ ) = 0, ℓ = 1, 2, …, n k paritásegyenletek alternatív leírása: Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom A c ( ℓ ) = 0 azt jelenti, hogy minden egyes kódszó polinomjában szerepelnek a Paritásellenőrzés GF(NM) számtestek gyöktényezők, azaz minden egyes kódszó előáll a alakban. 13

Széchenyi Információelmélet – Reed—Solomon-kódok István Paritásegyenletek Egyetem Reed— Solomon-kódok A Reed—Solomon-kódok minden egyes kódszava előáll a Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés alakban. A Reed—Solomon-kódok tehát tulajdonképpen ciklikus kódok, melyeknek a generátorpolinomja GF(NM) számtestek 14

Széchenyi Információelmélet – Reed—Solomon-kódok István Generátorpolinom Egyetem Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek A Reed—Solomon-kódunkhoz rendelhető, a (t n − 1) polinommal meghatározott ciklikus kód generátorpolinomja tehát gyöktényezős alakban: A (t n − 1) „alap”-polinom gyökei i -k, i=0, 1, …, n 1, tehát g(t ) gyökei t n − 1 -nek is gyökei lesznek, így g(t ) valóban osztója lesz t n − 1 -nek. Bizonyítás: ha az n kódszóhossz megegyezik a elem rendjével, akkor n =1. 15

Széchenyi Információelmélet – Reed—Solomon-kódok István Generátorpolinom Egyetem Reed— Solomon-kódok Generáló elemek Generálóelem Bizonyítás: ha az n kódszóhossz megegyezik a elem rendjével, akkor n =1. Így in=1, tehát ha (tn− 1)-ben t helyére -t, illetve bármely i-edik hatványát írjuk: Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek tehát bármely hatványa a (tn− 1) polinom gyöke. Ezek közül az 1 -től n−k-ig terjedő hatványokból alkotott gyöktényezők alkotják a generátorpolinomot: a többi adja a paritásellenőrző polinomot. 16

Széchenyi Információelmélet – Reed—Solomon-kódok István Paritásellenőrzés Egyetem A paritásellenőrző polinom tehát : Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek A GF(N) generálóelemmel definiált Reed— Solomon-kód paritásellenőrző mátrixa belátható, hogy G∙HT=0, így az állítás ellenőrizhető. 17

Széchenyi Információelmélet – Reed—Solomon-kódok István Matematikai kitérő – Egyetem A GF (N M ) véges számtestekről Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek Egy {0, 1, 2, …, N M 1} halmazon lehet úgy összeadást és szorzást definiálni, hogy véges testet alkosson. Rendeljünk hozzá a halmaz minden ele-méhez egy-egyértelműen a GF(P( t )) GF(N) feletti polinom-Galois-test elemei közül egyet, és úgy szorozzuk és adjuk össze a számokat, mint a nekik megfeleltetett polinomokat. Így tudunk nem prím, hanem prímszám egész hatványa elemszámú véges számtestet létrehozni (1 bájt=8 bit) 18

Széchenyi Információelmélet – Reed—Solomon-kódok István Matematikai kitérő – Egyetem A GF (N M ) véges számtestekről Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek Példa: másodfokú irreducíbilis polinom a t 2 + t + 1. A GF( 4 ) = GF( 22 ) véges test elemei a 0, 1, 2, 3 számok, bináris alakban 0 0, 0 1, 1 0 és 1 1. Minden számhoz rendeljünk egy legfeljebb 2 1=1 -fokú GF(2) feletti polinomot a következőképpen: ha a szám bináris alakja a b, akkor a hozzá rendelt polinom a ∙ t + b. Az összeadás a következő esetekben triviális: 19

Széchenyi Információelmélet – Reed—Solomon-kódok István Matematikai kitérő – Egyetem A GF (N M ) véges számtestekről Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Példa: GF( 4 ) = GF( 22 ) véges test, a t 2 + t + 1 másodfokú irreducíbilis polinommal. Összeadás esetén a mod 2 műveleteket is kell használni: Paritásellenőrzés GF(NM) számtestek A polinomos megfontolásokat csak néhány szorzás esetében kell használni: 20

Széchenyi Információelmélet – Reed—Solomon-kódok István Matematikai kitérő – Egyetem A szorzások: Reed— Solomon-kódok A GF (N M ) véges számtestekről Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek 21

Széchenyi Információelmélet – Reed—Solomon-kódok István Matematikai kitérő – Egyetem A szorzások: Reed— Sólomon-kódok A GF (N M ) véges számtestekről Generáló elemek Generálóelem Mivel az egység. Paritásegyenletek elem a 0 t+1, az Generátorpolinom inverzpárok: Paritásellenőrzés 01— 01 M) 10— 11 GF(N számtestek 22

Széchenyi Információelmélet – Reed—Solomon-kódok István Matematikai kitérő – Egyetem A szorzások: Reed— Sólomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek A GF (N M ) véges számtestekről Példa: GF( 4 ) = GF( 22 ) véges test, a t 2 + t + 1 másodfokú irreducíbilis polinommal. Összeadó- és szorzótábla: + 0 1 2 3 ∙ 0 1 2 3 0 0 0 1 1 0 3 2 1 0 1 2 3 2 2 3 0 1 2 0 2 3 1 3 3 2 1 0 3 1 2 23

Széchenyi Információelmélet – Reed—Solomon-kódok István Matematikai kitérő – Egyetem A GF (N M ) véges számtestekről Reed— Solomon-kódok Generáló elemek A GF( 28 ) bájtokat kezelni képes véges test GF(P( t )) polinom-Galois-testjének generáló irreducíbilis polinomja Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek Az p 7 p 6 p 5 p 4 p 3 p 2 p 1 p 0 bináris alakú számhoz a következő, GF( 2 ) feletti, legfeljebb hetedfokú polinomot rendeljük hozzá: Vegyük észre, hogy a fenti hozzárendelés tulajdonképpen egy bináris vektor – bináris polinom hozzárendelés: 8 elemű bináris vektor hetedfokú bináris polinom 24

Széchenyi Információelmélet – Reed—Solomon-kódok István Egyetem Reed—Solomon-kódok GF(NM) Reed— Solomon-kódok Generáló elemek Generálóelem Paritásegyenletek Generátorpolinom Paritásellenőrzés GF(NM) számtestek felett Reed—Solomon kódokat lehet nem csak prím, hanem prímhatvány elemszámú véges test felett is definiálni a GF(N) esettel analóg módon. A különbségek: • GF(NM) összeadó- és szorzótábla • GF(NM) hatványok • a generáló elemnek GF(NM)-ben kell n-edrendűnek lennie. 25

Információelmélet Nagy Szilvia 11. A Reed—Solomon-kódok spektruma és dekódolása 2005.

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Fourier-transzformálás véges testeken Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció Legyen a c=(c 0 , c 1 , …, c n− 1 ) GF(NM )-beli n komponensű vektor C =(C 0 , C 1 , …, C n− 1 ) (GF(NM ))n Fouriertranszformáltjának komponensei a A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása képlet szerint állnak elő, a véges test nedrendű eleme. Szokás a C Fourier-transzformáltat F {c}-ként írni és a c spektrumának nevezni. 27

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Fourier-transzformálás véges testeken Reed— Solomon-kódok II. Fouriertranszformáció Példa: számoljuk ki a c=(3 0 1 4) GF(5 )-beli 4 komponensű vektor Fourier-transzformáltjának komponenseit =3 -mal: Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 28

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Fourier-transzformálás véges testeken Reed— Solomon-kódok II. A Fourier-transzformációnak van inverz művelete: Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása ahol n− 1 az n-nek a GF(N M) véges testen belüli inverze. Bináris esetben, azaz ha N=2, n− 1=1 (ha n páratlan). Egyszerű hibák javítása 29

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. Fouriertranszformáció Legyen a t=(t 0 , t 1 , …, t n− 1 ) és u=(u 0 , u 1 , …, u M n− 1 ) két GF(N )-beli n komponensű vektor. Az s=t u ciklikus konvolúciója az az s =(s M n 0 , s 1 , …, s n− 1 ) (GF(N )) vektor, melynek komponensei: Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A ciklikus konvolúcióra érvényes a konvolúciós tétel: Ha az s, t, u vektorok Fouriertranszformáltjai rendre S, T, U, és a vektorok komponensei között fennáll, hogy akkor a spektrum vektorokra igaz, hogy 30

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. A konvolúciós tétel belátása: az s vektorok Fourier-transzformáltjának, S-nek az i-edik komponense Fouriertranszformáció Konvolúció A spektrum jellemzői behelyettesítve u-t, mint U-nak az inverz. Fourier-transzformáltját Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása ha j−k<0, akkor az nnel vett osztás utáni maradékát kell venni 31

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. Példa: adjuk meg az a=(3 0 1 4) és a b=(2 0 2 1) vektorok konvolúcióját GF(5) felett. (n=4, 4− 1≡ 4 mod 5. ) Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 32

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. Fouriertranszformáció Legyen a GF(NM )test n-edrendű eleme. Egy c (GF(NM ))n vektor spektrum-polinomja a C=(C 0 , C 1 , …, C n− 1 ) spektrumához rendelt legfeljebb n− 1 -edfokú polinom: Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 33

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői A GF(NM ) n-edrendű elem i-edik hatványa, i akkor és csak akkor lehet gyöke egy c( t ) polinomnak, ha a polinomhoz tartozó vektor C spektrumában az i-edik elem nulla: Bizonyítás: ha i gyöke c(t)-nek, akkor c( i) = 0. Kifejtve: Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása ami pont C i. 34

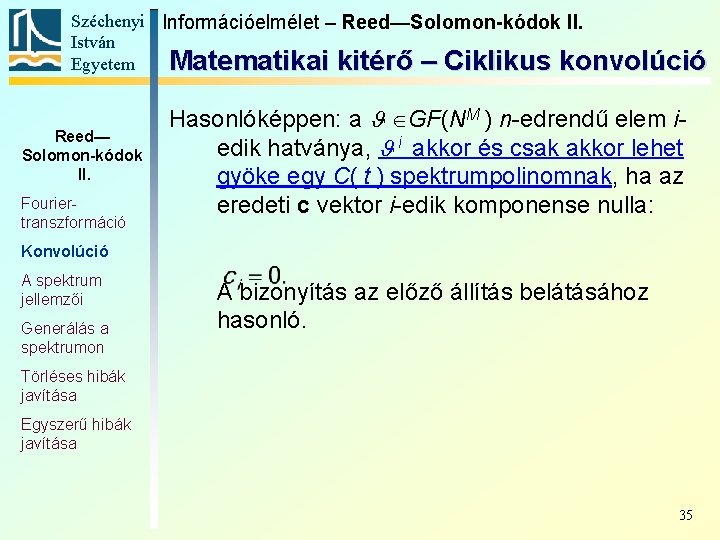
Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. Fouriertranszformáció Hasonlóképpen: a GF(NM ) n-edrendű elem iedik hatványa, i akkor és csak akkor lehet gyöke egy C( t ) spektrumpolinomnak, ha az eredeti c vektor i-edik komponense nulla: Konvolúció A spektrum jellemzői Generálás a spektrumon A bizonyítás az előző állítás belátásához hasonló. Törléses hibák javítása Egyszerű hibák javítása 35

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem A Reed—Solomon-kódok spektruma Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Legyen a Reed—Solomon-kód generátorpolinomja g( t ), a kódolandó üzenet polinomja b( t ), a hozzárendelt kódszópolinom c( t ). A c( t ) n− 1 -edfokú, b( t ) k− 1 -edfokú, g( t ) pedig n−k− 1 -edfokú. Az n− 1 -edfokú polinomok között a b( t )-nek és g( t )-nek az utolsó együtthatói nullák. Mindhárom polinom származtatható n komponensű vektorokból is: Törléses hibák javítása Egyszerű hibák javítása 36

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem A Reed—Solomon-kódok spektruma Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A Reed—Solomon-kód c( t ) kódszópolinomjai a következőképpen állíthatók elő: A polinomszorzás definíciója szerint az i-edfokú együttható: A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása ami g b i-edik komponense. Tehát c = g b. A konvolúciós tétel szerint ekkor a vektorok spektruma között a következő összefüggés áll fenn: 37

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem A Reed—Solomon-kódok spektruma Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Legyen a Reed—Solomon-kódot generáló és egyben a Fourier- transzformációt definiáló n -edrendű GF(NM )-beli elem . A generátorpolinomnak, s így minden kódszópolinomnak gyöke 1 -től n – kadikig terjedő hatványa. Így minden kódszóvektor spektrumának az 1 -től n – k-adikig terjedő indexű komponense nulla: Egyszerű hibák javítása 38

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem A Reed—Solomon-kódok spektruma Reed— Solomon-kódok II. Minden kódszóvektor spektrumának az 1 -től n – k-adikig terjedő indexű komponense nulla: Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása Ez a tény lehetővé teszi a kódszavak spektrumukon keresztül történő definiálását: a (b 0 , b 1 , …, b k− 1) üzenethez rendelt kódszó spektrumának – az első n−k eleme 0 – az utolsó k eleme b 0 , b 1 , …, b k− 1 39

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem A hibák javítása A paritásellenőrző mátrix: Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Ebből a szindróma: Törléses hibák javítása Elemenként kifejtve: Egyszerű hibák javítása Ismerve a szindróma n−k elemét, ennek az egyenletrendszernek kell a legkisebb súlyú Dc megoldását megkeresni 40

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Törléses hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása Törléses hibák esetén ismerjük azt, hogy Dc mely komponensei biztosan 0 -k és melyek nem azok. A 0 elemek a HT bármely oszlopával összeszorozva 0 járulékot adnak, így a velük azonos sorszámú sorokat törölhetjük HT-ből. Összesen legfeljebb n−k nem nulla elem van Dcben, így legfeljebb n−k sora marad a csonkolt HT-nek. Eleve csak n−k oszlopa volt, így négyzetes mátrix marad. Legyen a csonkolt paritásellenőrző mátrix Húzzuk ki Dc-ből is a 0 elemeket, az így kapott vektor: 41

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Törléses hibák javítása A kapott Reed— Solomon-kódok II. Fouriertranszformáció avagy Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása n−k változós egyenletrendszer megoldható. 42

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció A Reed—Solomon-kódok n <(n−k)/2 egyszerű hibát tudnak javítani. Tegyük fel, hogy az ℓ-edik helyen van hiba. Ekkor minden Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása egyenletben szerepel egy-egy nem 0 tag: ℓ-ből egyértelműen megadható a hiba helye, csak meg kell keresni, hogy hányadik hatványa -nak. A ℓ mennyiség a hibahely-lokátor 43

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Legyen Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása a hibahely-polinom, melynek gyökei a hibahelylokátorok inverzei. Ha meg tudjuk határozni L(t)-t, akkor • a gyökeit ki tudjuk számolni • meg tudjuk adni a gyökök inverzét, azaz a hibahely-lokátorokat • meg tudjuk keresni, hogy azok hányadik hatványai, azaz meg tudjuk adni, hol vannak hibák Ha a hibák helyét ismerjük, akkor törléses hibákat kell javítani, azt meg láttuk hogyan kell. 44

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása L-re igaz, hogy Reed— Solomon-kódok II. Fouriertranszformáció Szorozzuk mindkét oldalt Konvolúció A spektrum jellemzői Összegezzünk ℓ=1, 2, …, n –re Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása Helyettesítsük be L(t)=1+L 1 t+…+Ln tn polinom egyelőre ismeretlen együtthatóit: 45

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Szétszorozva hatványait: Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A szindróma a következő volt: 46

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Így kaptunk egyenletrendszert L(t) együtthatóira, amelyben csak a szindróma szerepel: Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása ahol j lehet 0, 1, …, n. A szindróma legmagasabb indexszel a j+n -vel fordul elő az egyenletrendszerben, ami legfeljebb 2 n lehet, ami nem haladja meg s komponenseinek a számát. (Hiszen legfeljebb (n−k)/2 egyszerű hiba javítható, a szindróma meg n−k komponensű. ) Az egyenletrendszer tehát mindig felírható. 47

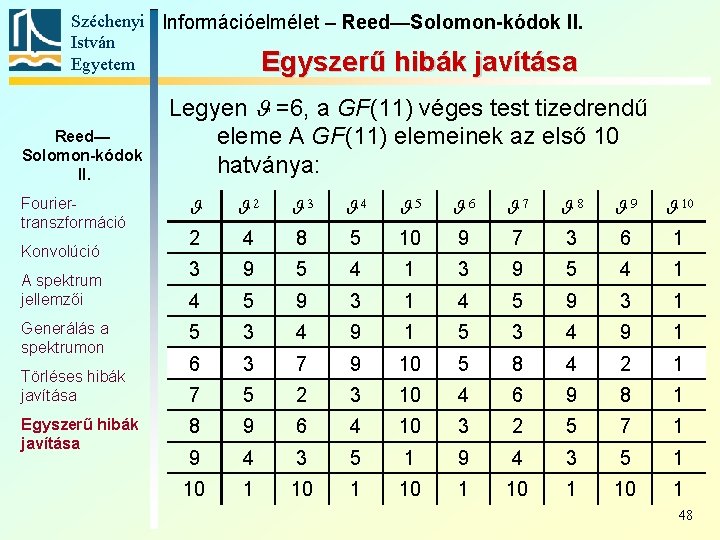
Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása Legyen =6, a GF(11) véges test tizedrendű eleme A GF(11) elemeinek az első 10 hatványa: 2 3 4 5 6 7 8 9 10 2 4 8 5 10 9 7 3 6 1 3 9 5 4 1 4 5 9 3 1 5 3 4 9 1 6 3 7 9 10 5 8 4 2 1 7 5 2 3 10 4 6 9 8 1 8 9 6 4 10 3 2 5 7 1 9 4 3 5 1 10 1 10 1 48

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Legyen =6, a GF(11) véges test feletti (10, 6) paraméterű Reed—Solomon-kód generáló eleme. A generátormátrix: Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A (0 2 6 7 1 1) üzenet által létrehozott kódszó: 49

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Legyen =6, a GF(11) véges test feletti (10, 6) paraméterű Reed—Solomon-kód generáló eleme. A paritásellenőrző mátrix: Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A (6 10 7 5 0 8 0 5 6 0) vett vektorból kapott szindróma: (233 108 230 141)≡ ≡(2 9 10 9). 50

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Dekódoljuk a =6 generáló elemű, GF(11) feletti (10, 6) Reed—Solomon-kód kódszavából torzult (6 10 7 5 0 8 0 5 6 0) vektort. A szindróma: (2 9 10 9). Konvolúció A spektrum jellemzői alkalmazása j=0 és 1 -re: Generálás a spektrumon Törléses hibák javítása azaz Egyszerű hibák javítása 51

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Dekódoljuk a =6 generáló elemű, GF(11) feletti (10, 6) Reed—Solomon-kód kódszavából torzult (6 10 7 5 0 8 0 5 6 0) vektort. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 52

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Dekódoljuk a =6 generáló elemű, GF(11) feletti (10, 6) Reed—Solomon-kód kódszavából torzult (6 10 7 5 0 8 0 5 6 0) vektort. A hibahelypolinom: Konvolúció A spektrum jellemzői Generálás a spektrumon Gyökei: 4 és 5: Törléses hibák javítása Egyszerű hibák javítása Inverzeik: 53

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása 2 3 4 5 6 7 8 9 10 Reed— Solomon-kódok II. 2 4 8 5 10 9 7 3 6 1 3 9 5 4 1 Fouriertranszformáció 4 5 9 3 1 5 3 4 9 1 6 3 7 9 10 5 8 4 2 1 7 5 2 3 10 4 6 9 8 1 8 9 6 4 10 3 2 5 7 1 9 4 3 5 1 10 1 10 1 Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A hibák tehát a 2. és 4. helyen vannak. 54

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A hibák tehát a 2. és 4. helyen vannak. A csonkolt paritásellenőrző mátrix: A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 55

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon A hibák tehát a 2. és 4. helyen vannak. A csonkolt paritásellenőrző mátrix: A csonkolt hibavektor: A szindróma (2 9 10 9) volt, Törléses hibák javítása Egyszerű hibák javítása 56

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon A hibák tehát a 2. és 4. helyen vannak. A csonkolt paritásellenőrző mátrix: A csonkolt hibavektor: A szindróma (2 9 10 9) volt, Törléses hibák javítása Egyszerű hibák javítása 57

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Behelyettesítés után: Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 58

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Átrendezve: Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A többi egyenletbe behelyettesítve az eredmény ellenőrizhető. 59

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Dekódoljuk a =6 generáló elemű, GF(11) feletti (10, 6) Reed—Solomon-kód kódszavából torzult (6 10 7 5 0 8 0 5 6 0) vektort. A hibavektor komponensei: Konvolúció A spektrum jellemzői Generálás a spektrumon A javított kódszó: Törléses hibák javítása (6 10 1 5 3 8 0 5 6 0) Egyszerű hibák javítása 60

Információelmélet Nagy Szilvia 12. A hibacsomók elleni védekezés 2005.

Széchenyi Információelmélet – Hibacsomók elleni védekezés István Egyetem Hibacsomók elleni védekezés Hibacsomó Többutas kódátfűzés Blokkos kódátfűzés CD-k hibavédelme Egy szimbólumsorozatban több, egymás után előforduló hibából álló sorozat a hibacsomó. Egy hosszabb hibacsomó javítása csak rendkívül hosszú kódszavakkal és főleg hosszú paritásszegmenssel lehetséges – hacsak szét nem bontjuk valahogy. Azokat az eljárásokat, amelyek során a kódolandó, illetve dekódolandó szimbólumsorozatot úgy módosítják, hogy az esetleg előforduló hibacsomók szétoszoljanak több kódszó között, kódátfűzésnek vagy interleavingnek hívjuk. 62

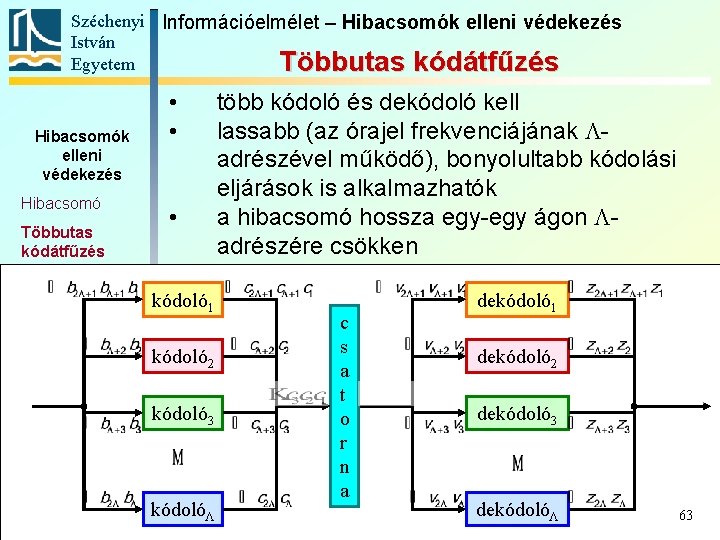
Széchenyi Információelmélet – Hibacsomók elleni védekezés István Egyetem Többutas kódátfűzés Hibacsomók elleni védekezés Hibacsomó Többutas kódátfűzés Blokkos kódátfűzés CD-k hibavédelme • • • kódoló 1 kódoló 2 kódoló 3 kódolóL több kódoló és dekódoló kell lassabb (az órajel frekvenciájának Ladrészével működő), bonyolultabb kódolási eljárások is alkalmazhatók a hibacsomó hossza egy-egy ágon Ladrészére csökken c s a t o r n a dekódoló 1 dekódoló 2 dekódoló 3 dekódolóL 63

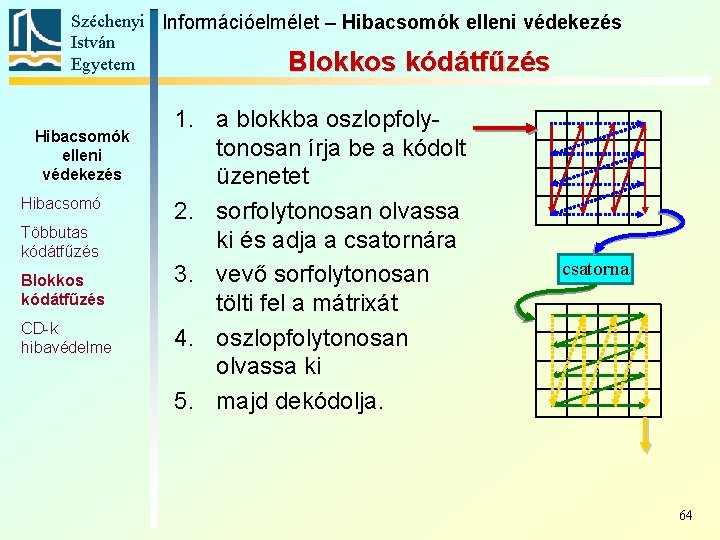
Széchenyi Információelmélet – Hibacsomók elleni védekezés István Egyetem Blokkos kódátfűzés Hibacsomók elleni védekezés Hibacsomó Többutas kódátfűzés Blokkos kódátfűzés CD-k hibavédelme 1. a blokkba oszlopfolytonosan írja be a kódolt üzenetet 2. sorfolytonosan olvassa ki és adja a csatornára 3. vevő sorfolytonosan tölti fel a mátrixát 4. oszlopfolytonosan olvassa ki 5. majd dekódolja. csatorna 64

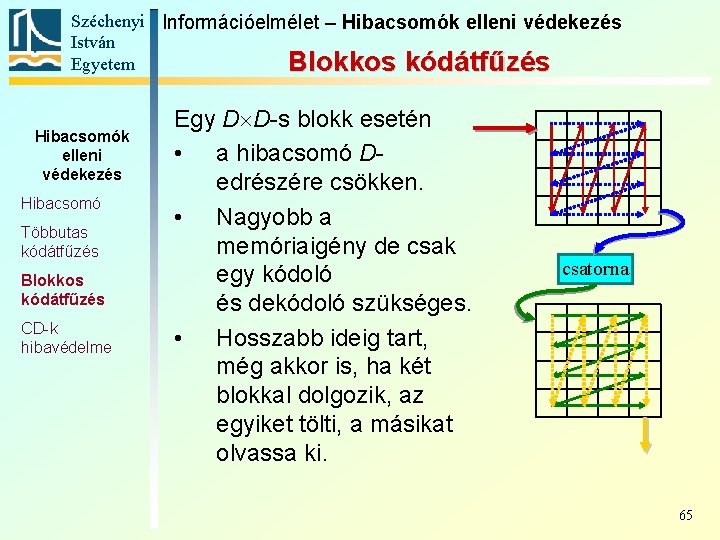
Széchenyi Információelmélet – Hibacsomók elleni védekezés István Egyetem Blokkos kódátfűzés Hibacsomók elleni védekezés Hibacsomó Többutas kódátfűzés Blokkos kódátfűzés CD-k hibavédelme Egy D D-s blokk esetén • a hibacsomó Dedrészére csökken. • Nagyobb a memóriaigény de csak egy kódoló és dekódoló szükséges. • Hosszabb ideig tart, még akkor is, ha két blokkal dolgozik, az egyiket tölti, a másikat olvassa ki. csatorna 65

Széchenyi Információelmélet – Hibacsomók elleni védekezés István Egyetem Hibacsomók elleni védekezés: CD-k Hibacsomók elleni védekezés Hibacsomó Többutas kódátfűzés Blokkos kódátfűzés CD-k hibavédelme A CD-kre írandó hangot 44, 1 k. Hz frekvenciával mintavételezik, két bájtra kvantálják. Sztereó – két hangcsatornás: jobb és bal – rendszerek esetén a következő sorrendbe rendezik a két csatorna egy-egy mintavételezési pontjához tartozó két-két bájtját: jobb 1. bájt, jobb 2. bájt, bal 1. bájt, bal 2. bájt, jelöljük őket x i 1 , x i 2 , y i 1 , y i 2 -vel (i-edik időpont). Minden érték GF(28). 66

Széchenyi Információelmélet – Hibacsomók elleni védekezés István Egyetem Hibacsomók elleni védekezés: CD-k 1. Hibacsomók elleni védekezés 2. Hibacsomó Többutas kódátfűzés Blokkos kódátfűzés CD-k hibavédelme 3. 4. Ezekkel az adatokkal feltöltenek egy 24 24 es mátrixot oszlopfolytonosan. Oszloponként (24, 28) paraméterű, GF(28) feletti Reed—Solomon-kóddal kódolják az adatokat 28 24 -es mátrix. A kapott mátrix sorait is kódolják az iménti R —S-kóddal. 28 28 -as mátrix. Soronként kiolvasva engedik a csatornára. A (24, 28)-as kóddal 2 egyszerű és 4 törléses hibát lehet kijavítani. 67

Széchenyi Információelmélet – Hibacsomók elleni védekezés István Egyetem Hibacsomók elleni védekezés: CD-k 1. Hibacsomók elleni védekezés 2. Hibacsomó Többutas kódátfűzés Blokkos kódátfűzés CD-k hibavédelme 3. A vett adatokkal sorfolytonosan feltöltenek egy 28× 28 -as blokkot Soronként megnézik a szindrómát. Ha • s=0, a sort békén hagyják • s=1, a hibát kijavítják • s=2, a hibák helyét határozzák meg, oda törlésés hibát generálnak • s>2, az egész sorba törléses hibát generálnak Oszloponként ha a törléses hibák száma • 1 vagy 2, akkor azt kijavítják • ha több, interpolálnak, mert az gyorsabb (és a fül elég tehetetlen) 68

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: Huffman-kód Egyetem Legyen a forrásábécé elemeinek előfordulási valószínűsége rendre p (p) =0, 31, p (r) =0, 15, p (s) =0, 11, p (t) =0, 19, és p (w) =0, 24. 69

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: Aritmetikai Egyetem kód Legyen a forrásábécé elemeinek előfordulási valószínűsége rendre p (l) =0, 25, p (m) =0, 125, p (n) =0, 0625, p (o) =0, 1875, és p (p) =0, 375. Rendeljük az egyes elemekhez, ilyen sorrendben a [0, 1) intervallumnak az elem valószínűségével azonos hosszát. Kódoljuk a „p o l o” üzenetet a kapott aritmetikai kóddal. 70

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: LZ 78 Egyetem kód Kódoljuk a „j b c j j b c c j b c” üzenetet LZ 78 eljárással. tüntessük fel az egyes lépésekben a kódoló kimenetén megjelenő értéket is. Használjuk az alábbi táblázatot. Adjuk meg a kódoló kimenetét. n m karakter sorozat 71

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: LZW Egyetem kód Kódoljuk az „ 5 7 7 2 5” üzenetet LZW eljárással. tüntessük fel az egyes lépésekben a kódoló kimenetén megjelenő értéket is. Használjuk az alábbi táblázatot: n m karakter kimenet 72

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: Hamming-kód Egyetem Hozzunk létre egy szisztematikus Hamming-kódot a GF(13) számtest felett. Legyen a paritásszegmens hossza 2. Mi a paritásellenőrző mátrix és mi a generátormátrix? Hány elemű az üzenetszegmens? Mi lesz a csupa 1 -esből álló üzenethez rendelt kódszó? 73

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: Hamming-kód Egyetem Adjuk meg a szisztematikus generátormátrixhoz tartozó paritásellenőrző mátrixot. Milyen véges test felett definiálták a kódot? Adjuk meg az „ 11 0 0 0 11” vett bitsorozat szindrómáját. Mi lehetett az eredeti kódszó? Milyen üzenetből jöhetett létre az iménti vett 74 bitsorozat?

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: Hamming-kód Egyetem Adjuk meg a szisztematikus generátormátrixhoz tartozó paritásellenőrző mátrixot. Milyen véges test felett definiálták a kódot? Adjuk meg az „ 2 4 3 5 1 6 2 0” vett bitsorozat szindrómáját. Mi lehetett az eredeti kódszó? Milyen üzenetből jöhetett létre az iménti vett bitsorozat? 75

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: Ciklikus Egyetem kód Azt tesszük fel, hogy a GF(5) felett a „ 3 1 3 0 4 0” egy ciklikus kód érvényes kódszava. Milyen polinomot tudunk a kódszóhoz rendelni? Két ciklikus eltolás után mi lesz a polinomból? Ha a ciklikus kód generátorpolinomja g(t)=t 2+4 t+1, valóban kódszó-e „ 3 1 3 0 4 0”? Mi a kód paritásellenőrző polinomja? Mennyi a „ 3 1 3 0 4 0”-hez rendelt polinom szindrómája? 76

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: Ciklikus Egyetem kód Egy 7 elemű kódszavakat generáló bináris ciklikus kód generátorpolinomja g(t)=t 3+t+1. Adjuk meg az 1 1 0 1 vektorból általa előállított kódszópolinomot. Mi a paritásellenőrző polinom? Mi t 6+t 5+t 3+1 vett polinom szindrómapolinomja? 77

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: R—S-kód Egyetem A GF(11) véges testben a 2 tizedrendű elem. Legyen 2 egy a GF(11) feletti Reed—Solomon-kódoló generáló eleme. Adjuk meg a b=(3 0 1 8) üzenethez generált tízelemű kódszót. 78

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: R—S-kód Egyetem A GF(5) véges testben a 3 negyedrendű elem. Legyen 3 egy a GF(7) feletti Reed—Solomon-kódoló generáló eleme, s egyben a Fourier-transzformáció definíciójában szereplő elem. Adjuk meg a b=(2 2 3) üzenethez a spektrumon keresztül generált négyelemű kódszót. Adjuk meg a spektrumot is. 79

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: R—S-kód Egyetem A GF(4) véges testben a 3 harmadrendű elem. Legyen 3 egy a GF(4) feletti Reed—Solomon-kódoló generáló eleme, s egyben a Fourier-transzformáció definíciójában szereplő elem. Adjuk meg a b=(2 3) a kódoló által generált háromelemű kódszót. Adjuk meg a spektrumot is. Használjuk az alábbi szorzó és összeadó táblázatokat: + 0 1 2 3 ∙ 0 1 2 3 0 0 0 1 1 0 3 2 1 0 1 2 3 2 2 3 0 1 2 0 2 3 1 3 3 2 1 0 3 1 2 80

Információelmélet Nagy Szilvia 13. Konvolúciós kódolás 2005.

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Keret, kódszókeret, kódsebesség Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló A konvolúciós kódolás során a tömörített b 1 , b 2 , b 3 , … üzenetet k bites szakaszokra – üzenetszegmensekre – bontjuk, és m+1 egymás utáni üzenetszegmensből alakítjuk ki a kódoló aktuális kimenetét. A kódoló mindig m darab k hosszúságú üzenetszegmenst – keretet – tárol, és egy van a bemenetén. Szabad távolság Komplex kódábécé 82

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Keret, kódszókeret, kódsebesség Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé Egy lépés során a kódoló • beolvas egy üzenetszegmenst • az m+1 darab, k hosszúságú bitsorozatból létrehoz egy n hosszúságú kimeneti bitsorozatot, a kódszókeretet. A kódsebesség: R = k/n. • eldobja a legrégebben tárolt keretet és elraktározza az újonnan beolvasottat Egy üzenetszegmens m+1 lépés során befolyásolja a kimenetet, utána tűnik csak el a tárolókból. A kódoló kényszerhossza K = k (m+1) bit. 83

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Kényszerhossz, fa-kód, trellis Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé Ugyanez az üzenetszegmens a kimeneten n (m+1) bit kialakításában vesz részt, az N = n (m+1) mennyiség a kódoló blokkhossza. Engedjük a kódoló bemenetére az összes lehetséges, nullával kezdődő félig végtelen bitsorozatot, és vizsgáljuk a kimeneti félig végtelen bitsorozatokat. A fa-kód ezek között a bemeneti és kimeneti sorozatok közötti hozzárendelés; a legegyszerűbben bináris fa formájában adható meg. Trellis-kódok a véges kényszerhosszú fa-kódok. 84

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Kódparaméterek Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé A K kényszerhosszú, N blokkhosszú, lineáris, időinvariáns trellis kódokat (N, K) paraméterű konvolúciós kódoknak nevezzük. • A konvolúciós kódok tervezése sok esetben lehetőséget nyújt a moduláció tervezésére is. • Lehet nem bináris konvolúciós kódokat is tervezni, de a kódfája akkor nem bináris lesz. Gyakorlatban nem alkalmazzák. • A konvolúciós kódolók létrehozhatók léptetőregiszterekkel, például: k=1, n=2, m=2, K=3, N=6 -ra 85

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Kódparaméterek Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf • A konvolúciós kódolók létrehozhatók léptetőregiszterekkel, például: k=1, n=2, m=2, K=3, N=6 -ra Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 86

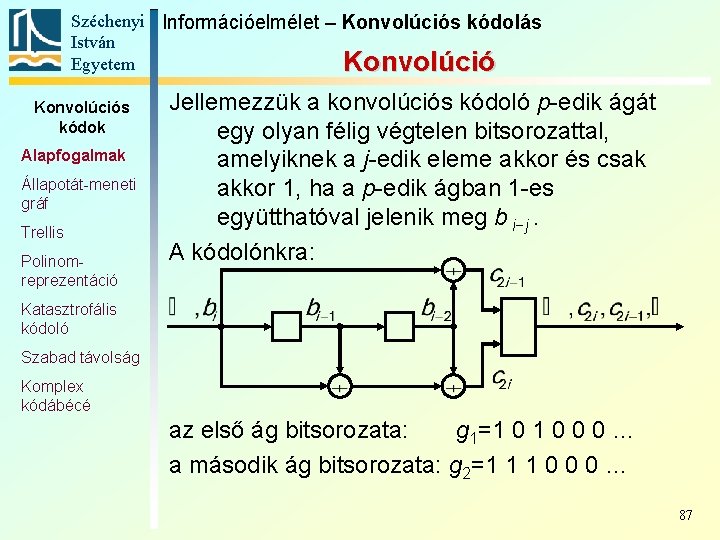
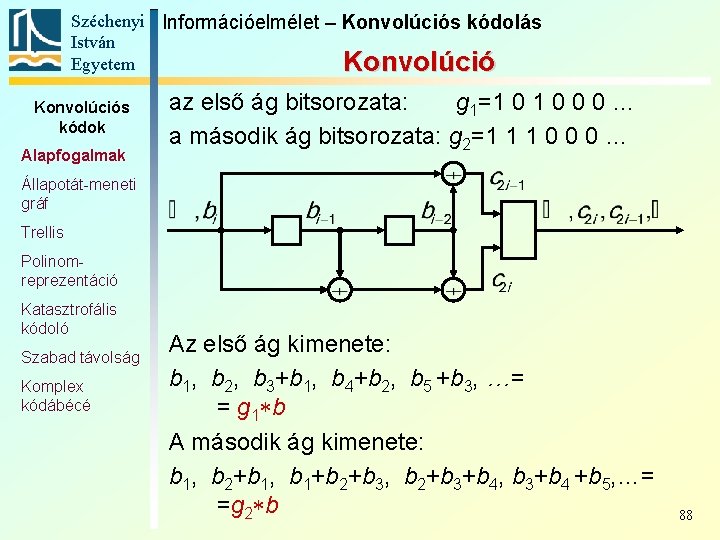
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Jellemezzük a konvolúciós kódoló p-edik ágát egy olyan félig végtelen bitsorozattal, amelyiknek a j-edik eleme akkor és csak akkor 1, ha a p-edik ágban 1 -es együtthatóval jelenik meg b i−j. A kódolónkra: Katasztrofális kódoló Szabad távolság Komplex kódábécé az első ág bitsorozata: g 1=1 0 0 0 … a második ág bitsorozata: g 2=1 1 1 0 0 0 … 87

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Alapfogalmak az első ág bitsorozata: g 1=1 0 0 0 … a második ág bitsorozata: g 2=1 1 1 0 0 0 … Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé Az első ág kimenete: b 1, b 2, b 3+b 1, b 4+b 2, b 5 +b 3, …= = g 1 b A második ág kimenete: b 1, b 2+b 1, b 1+b 2+b 3, b 2+b 3+b 4, b 3+b 4 +b 5, …= =g 2 b 88

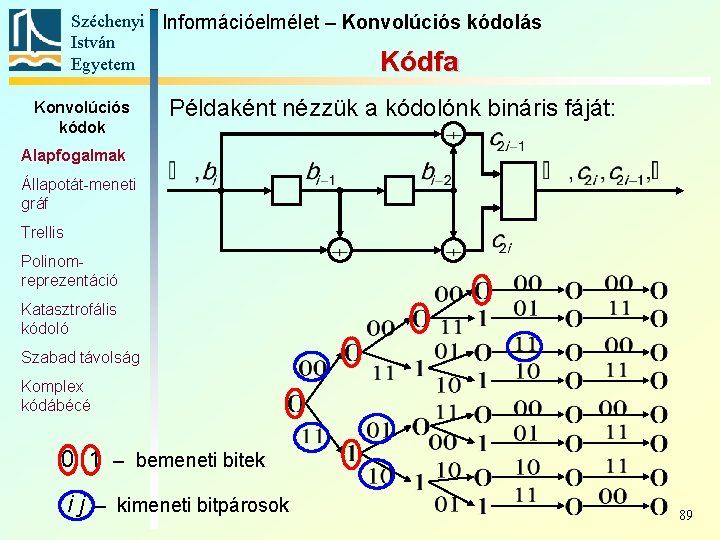
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Kódfa Konvolúciós kódok Példaként nézzük a kódolónk bináris fáját: Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 0 1 – bemeneti bitek i j – kimeneti bitpárosok 89

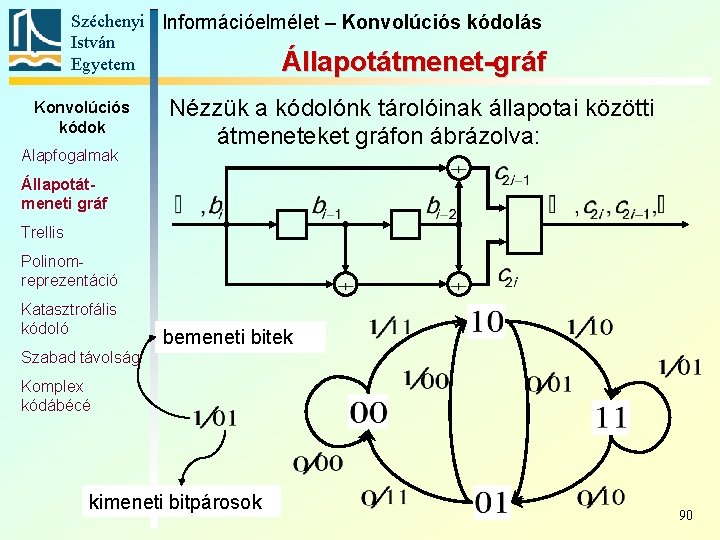
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Állapotátmenet-gráf Konvolúciós kódok Alapfogalmak Nézzük a kódolónk tárolóinak állapotai közötti átmeneteket gráfon ábrázolva: Állapotátmeneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló bemeneti bitek Szabad távolság Komplex kódábécé kimeneti bitpárosok 90

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Trellis diagram Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinoma trellisnek ezen reprezentáció Az állapotátmenet-gráfról, vagy az áramkör blokkváz-latáról leolvashatók a különféle bemeneti kombinációk hatására a kimeneten és a tárolókban megjelent bitek, melyeket a trellisen lehet ábrázolni: része tetszőleges Katasztrofális számszor kódoló ismételhető Szabad távolság Komplex kódábécé a tárolók kiürítése 91

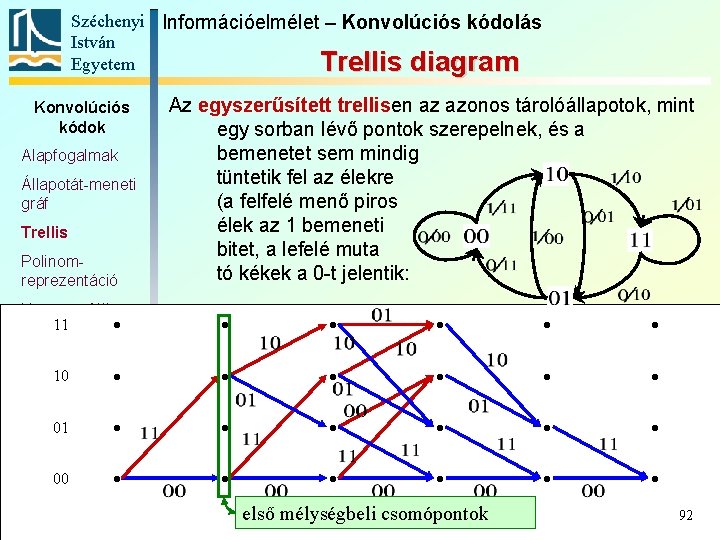
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Trellis diagram Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális 11 kódoló Szabad távolság 10 Komplex kódábécé 01 00 Az egyszerűsített trellisen az azonos tárolóállapotok, mint egy sorban lévő pontok szerepelnek, és a bemenetet sem mindig tüntetik fel az élekre (a felfelé menő piros élek az 1 bemeneti bitet, a lefelé muta tó kékek a 0 -t jelentik: első mélységbeli csomópontok 92

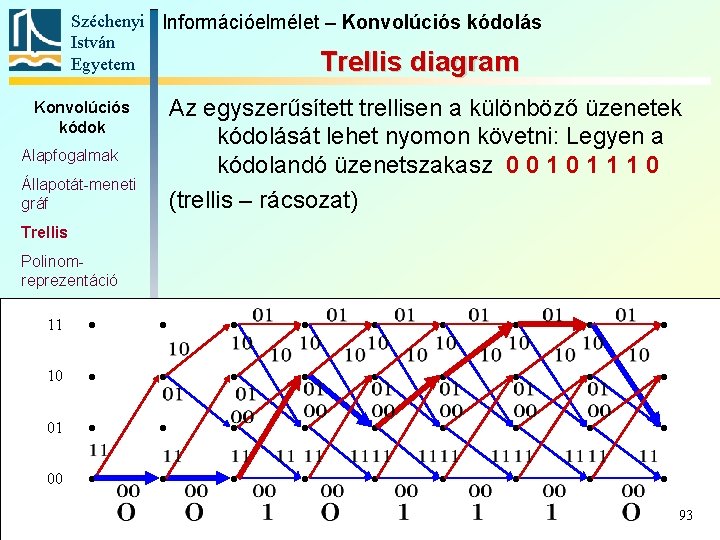
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Trellis diagram Az egyszerűsített trellisen a különböző üzenetek kódolását lehet nyomon követni: Legyen a kódolandó üzenetszakasz 0 0 1 1 1 0 (trellis – rácsozat) Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális 11 kódoló Szabad távolság 10 Komplex kódábécé 01 00 93

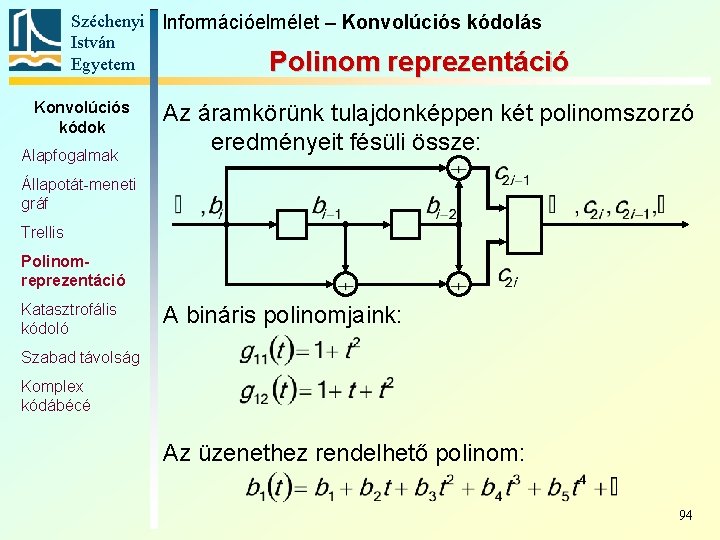
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Polinom reprezentáció Konvolúciós kódok Alapfogalmak Az áramkörünk tulajdonképpen két polinomszorzó eredményeit fésüli össze: Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló A bináris polinomjaink: Szabad távolság Komplex kódábécé Az üzenethez rendelhető polinom: 94

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Polinom reprezentáció Konvolúciós kódok Az ágakat jellemző bináris polinomok: Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Az üzenethez rendelhető polinom: Katasztrofális kódoló Szabad távolság Komplex kódábécé Az kimenet szétosztható 2 darab külön bitfolyamra, melyekhez a következő polinomok rendelhetők: 95

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Polinom reprezentáció Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Ha hosszabb az üzenetkeret, az üzenetet is k darab különálló bitfolyamra kell bontani, és a generáló polinomoknak is két fontos indexe lesz. Ezek a polinomok mátrixba rendezhetők: Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé A mátrix első sora jellemzi az első bemeneti bit hatását az n darab kimenetre, a második sor a második bemeneti bitét, … 96

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Polinom reprezentáció Konvolúciós kódok A kódoló polinom-mátrixa: Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Az üzenethez és a kimenethez rendelhető polinomok vektorokba rendezhetők: Szabad távolság Komplex kódábécé Így 97

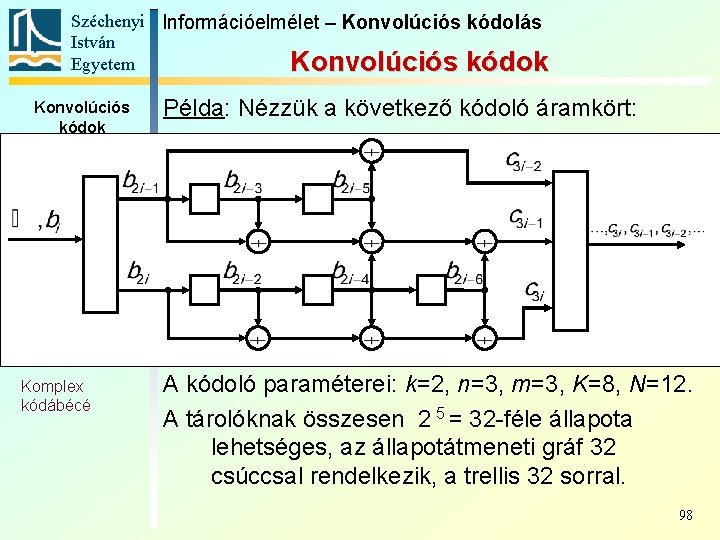
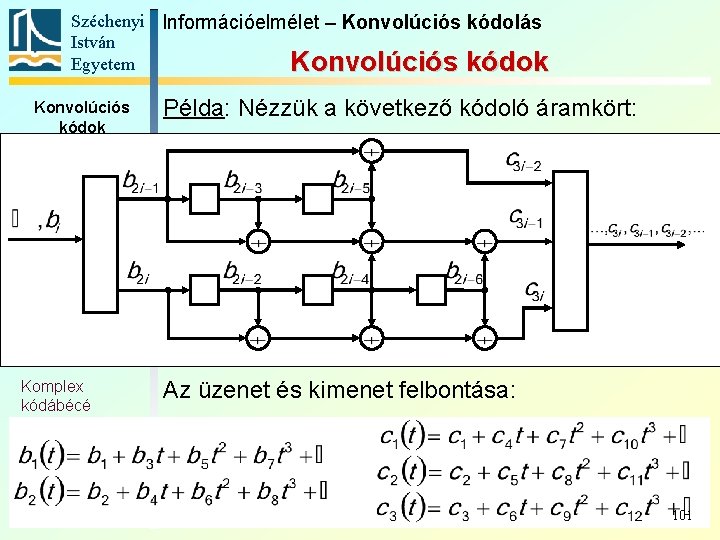
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Példa: Nézzük a következő kódoló áramkört: Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé A kódoló paraméterei: k=2, n=3, m=3, K=8, N=12. A tárolóknak összesen 2 5 = 32 -féle állapota lehetséges, az állapotátmeneti gráf 32 csúccsal rendelkezik, a trellis 32 sorral. 98

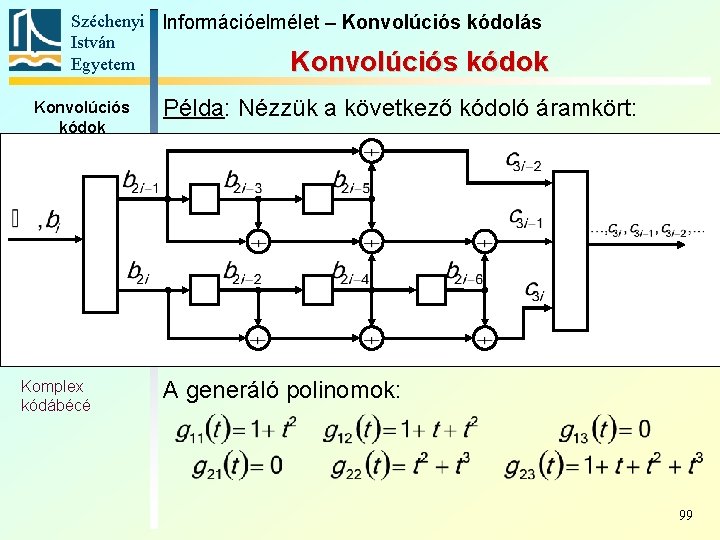
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Példa: Nézzük a következő kódoló áramkört: Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé A generáló polinomok: 99

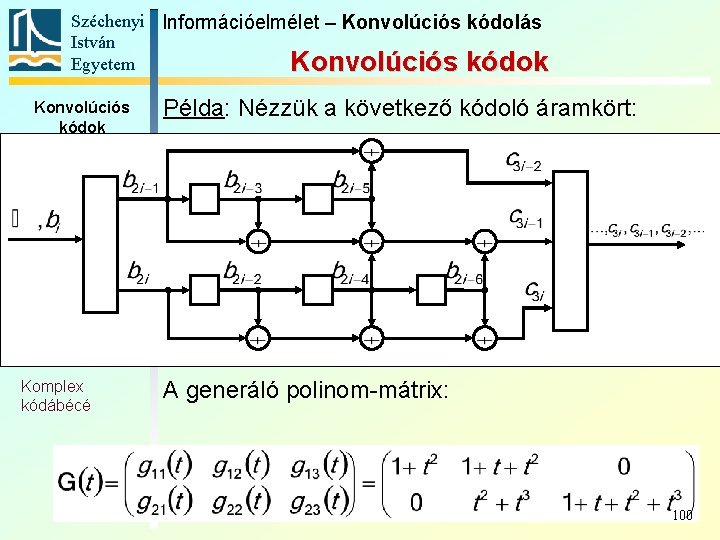
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Példa: Nézzük a következő kódoló áramkört: Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé A generáló polinom-mátrix: 100

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Példa: Nézzük a következő kódoló áramkört: Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé Az üzenet és kimenet felbontása: 101

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Példa: Nézzük a következő kódoló áramkört: Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé Az üzenethez két-, a kimenethez három komponensű polinom-vektor tartozik: 102

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Példa: A polinom-mátrix: Alapfogalmak Állapotát-meneti gráf Trellis A kód komponensei: Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 103

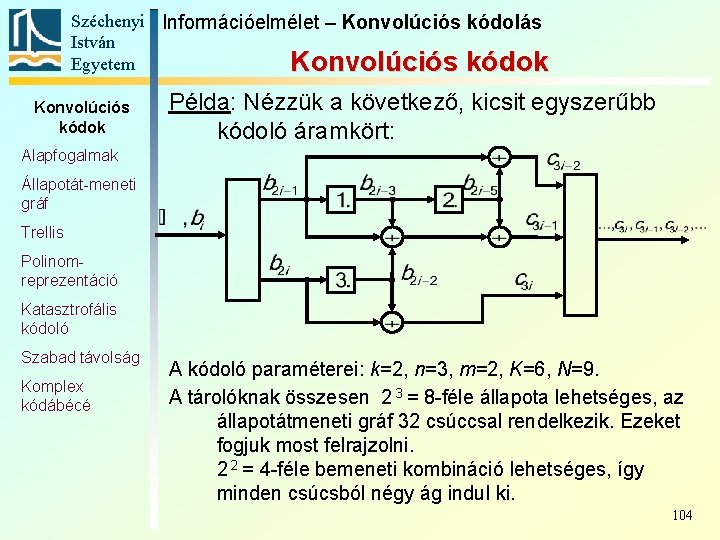
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Példa: Nézzük a következő, kicsit egyszerűbb kódoló áramkört: Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé A kódoló paraméterei: k=2, n=3, m=2, K=6, N=9. A tárolóknak összesen 2 3 = 8 -féle állapota lehetséges, az állapotátmeneti gráf 32 csúccsal rendelkezik. Ezeket fogjuk most felrajzolni. 2 2 = 4 -féle bemeneti kombináció lehetséges, így minden csúcsból négy ág indul ki. 104

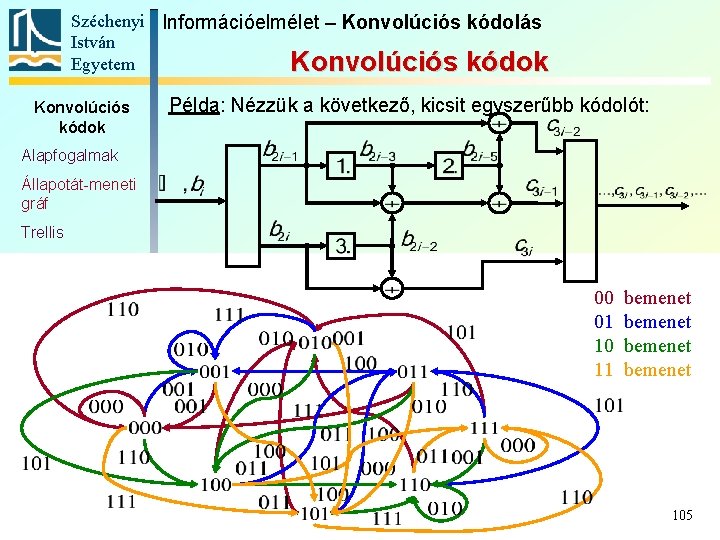
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Példa: Nézzük a következő, kicsit egyszerűbb kódolót: Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 00 01 10 11 bemenet 105

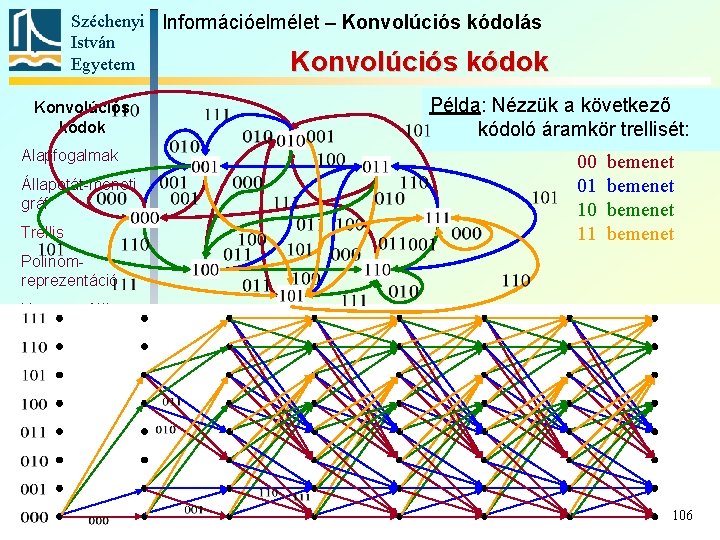
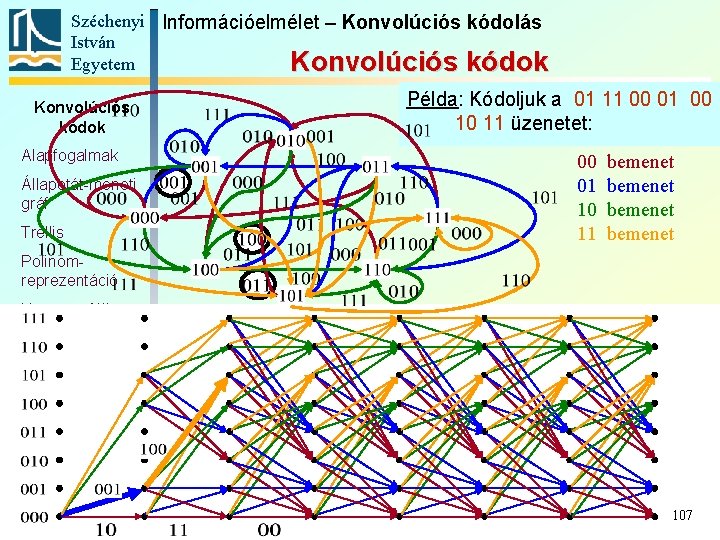
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Példa: Nézzük a következő kódoló áramkör trellisét: 00 01 10 11 bemenet Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 106

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Példa: Kódoljuk a 01 11 00 01 00 10 11 üzenetet: 00 01 10 11 bemenet Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 107

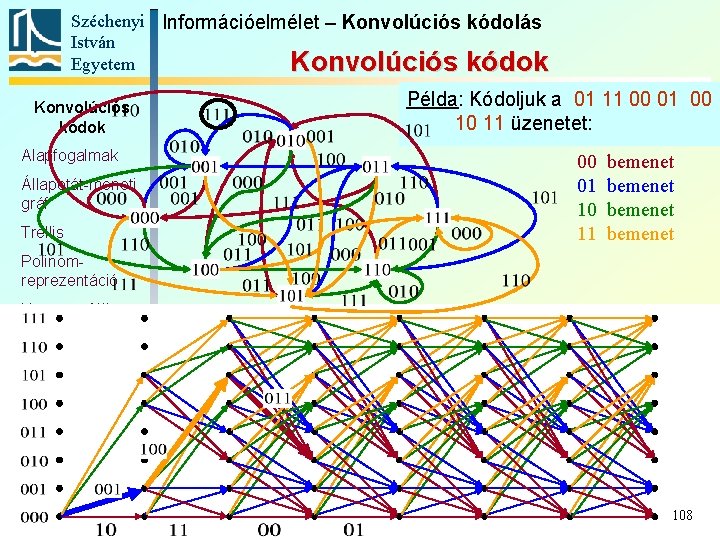
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Példa: Kódoljuk a 01 11 00 01 00 10 11 üzenetet: 00 01 10 11 bemenet Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 108

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Példa: Kódoljuk a 01 11 00 01 00 10 11 üzenetet: 00 01 10 11 bemenet Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 109

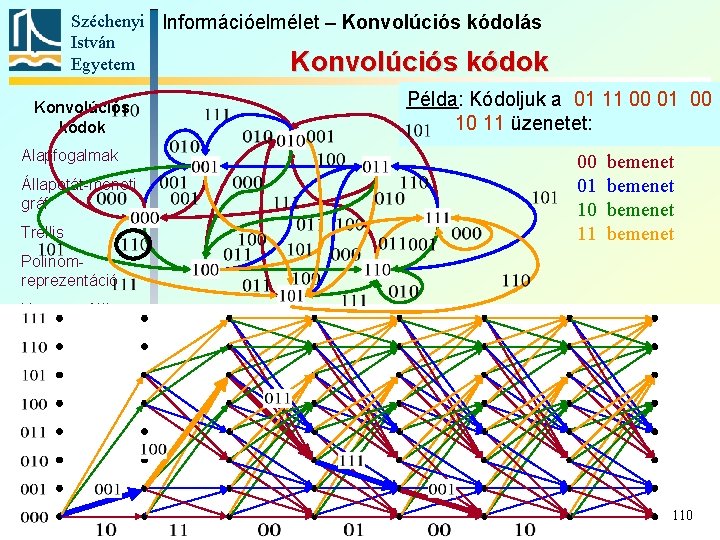
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Példa: Kódoljuk a 01 11 00 01 00 10 11 üzenetet: 00 01 10 11 bemenet Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 110

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Példa: Kódoljuk a 01 11 00 01 00 10 11 üzenetet: 00 01 10 11 bemenet Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 111

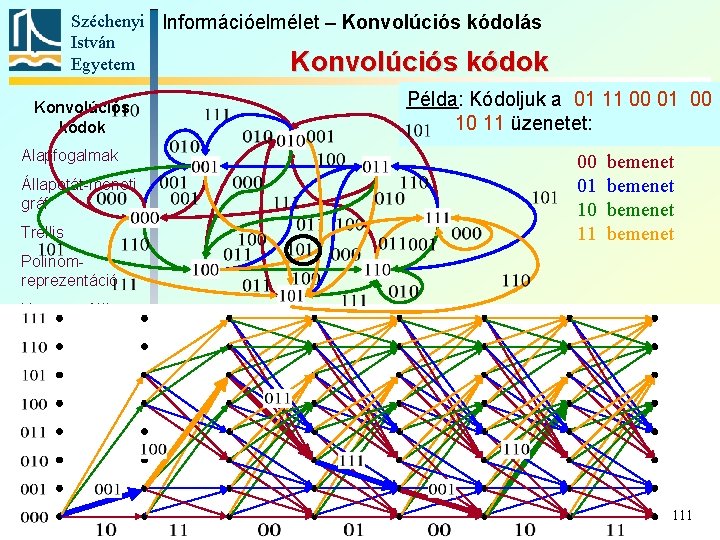
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Példa: Kódoljuk a 01 11 00 01 00 10 11 üzenetet: 00 01 10 11 bemenet Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 112

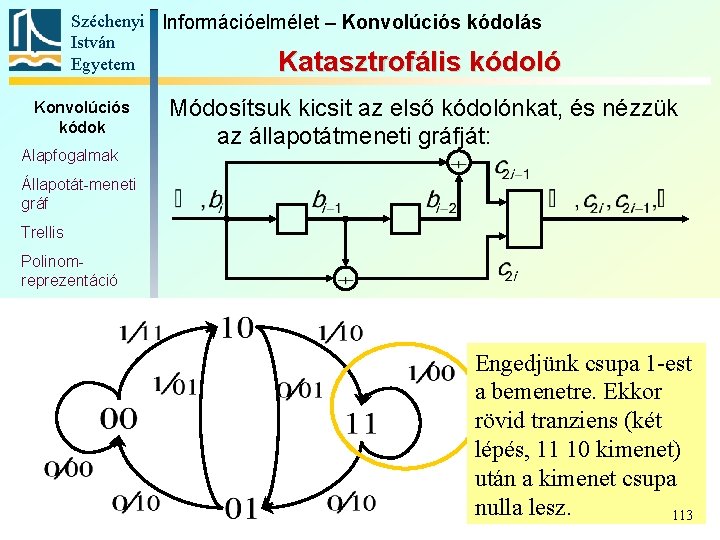
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Katasztrofális kódoló Konvolúciós kódok Alapfogalmak Módosítsuk kicsit az első kódolónkat, és nézzük az állapotátmeneti gráfját: Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé Engedjünk csupa 1 -est a bemenetre. Ekkor rövid tranziens (két lépés, 11 10 kimenet) után a kimenet csupa nulla lesz. 113

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Katasztrofális kódoló Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé Az olyan kódolókat amelyek nem csak tiszta nulla bemenetre, hanem valamilyen más, periodikus bemeneti sorozatra is tiszta nulla kimenetet adnak, katasztrofális kódolóknak nevezik. A katasztrofális kódolónak az állapotátmeneti gráfján mindig van egy olyan hurok, amelyik nem a tiszta nulla állapotból indul és mégis tiszta nulla a kimenete, azaz nulla a hurok kimenetének Hamming 114 súlya.

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Katasztrofális kódoló Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé A katasztrofális kódoló pontos definíciója: Az olyan kódolók, melyek tetszőlegesen nagy Hamming-súlyú bemenetre is korlátos Hamming-súlyú maradhat a kimenet. (l. a kódolónkra bármennyi 1 -est engedünk, a kimenet lehet 3 -nál nem nagyobb súlyú. ) Szeretnénk elkerülni a katasztrofális kódolókat, ezért szeretnénk egy olyan feltételt, amely az állapotátmenet-gráf (hosszadalmas) felrajzolása nélkül is megmondja, hogy katasztrofális-e a kódoló vagy nem. 115

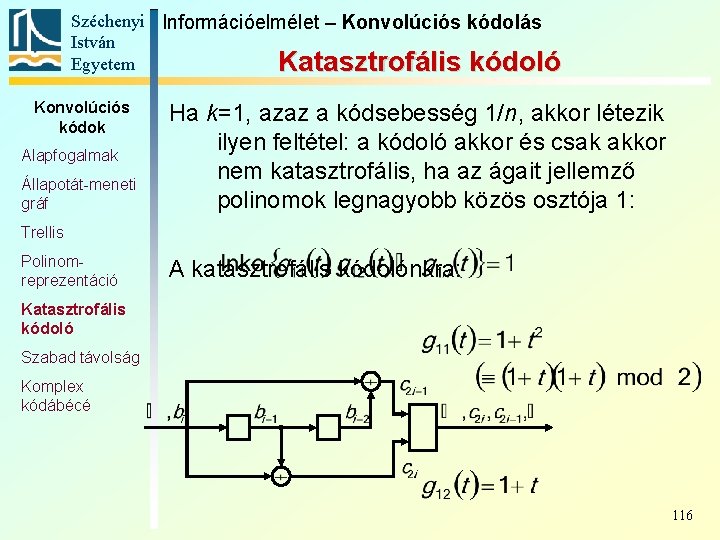
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Katasztrofális kódoló Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Ha k=1, azaz a kódsebesség 1/n, akkor létezik ilyen feltétel: a kódoló akkor és csak akkor nem katasztrofális, ha az ágait jellemző polinomok legnagyobb közös osztója 1: Trellis Polinomreprezentáció A katasztrofális kódolónkra: Katasztrofális kódoló Szabad távolság Komplex kódábécé 116

Információelmélet Nagy Szilvia 14. Viterbi-algoritmus 2005.

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Távolságprofil, szabad távolság Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé Vizsgáljuk a kódoló lehetséges kimeneteiből mindig az első r kódszókeretet. Az így kapott r ∙n hosszúságú vektoroknak értelmezhető a Hamming-távolsága. Jelöljük ezek közül a minimálisat dr*-gal. Ekkor r növelésével ez a minimális távolság nem fog csökkenni: A d 1*, d 2*, d 3*, … sorozatot a kódoló távolságprofiljának nevezik. A dr*-okból álló monoton növekvő sorozat határértéke, avagy ezen értékek maximuma a kód szabad távolsága: 118

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Kódolási nyereség Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció A csatornakódolás során ezesetben is a kódtávolság növelésére törekedünk. Vegyük a kódolatlan üzenet dref szabad távolságát referenciának. A kódolási nyereség: Katasztrofális kódoló Szabad távolság Komplex kódábécé a kódolt üzenet szabad kódtávolságá-nak és a referenciatávolság aránya decibelskálán. 119

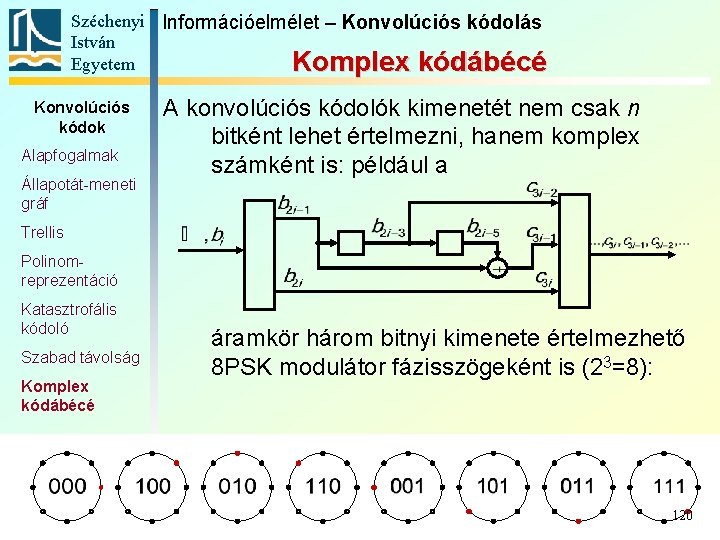
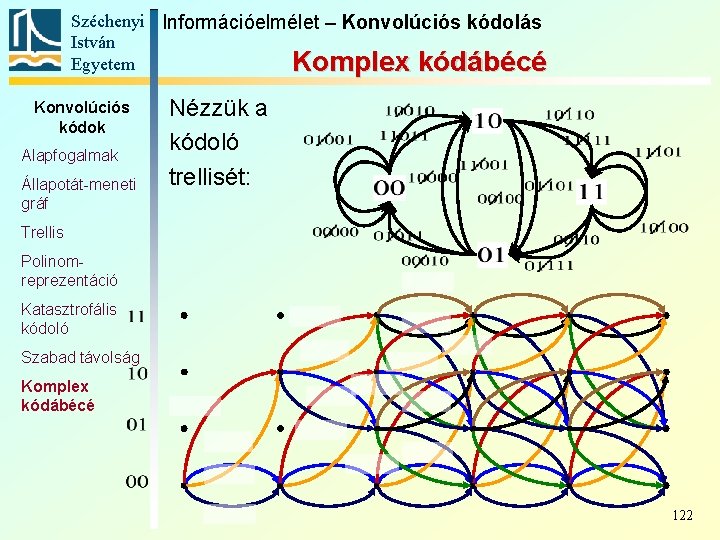
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Komplex kódábécé Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf A konvolúciós kódolók kimenetét nem csak n bitként lehet értelmezni, hanem komplex számként is: például a Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé áramkör három bitnyi kimenete értelmezhető 8 PSK modulátor fázisszögeként is (23=8): 120

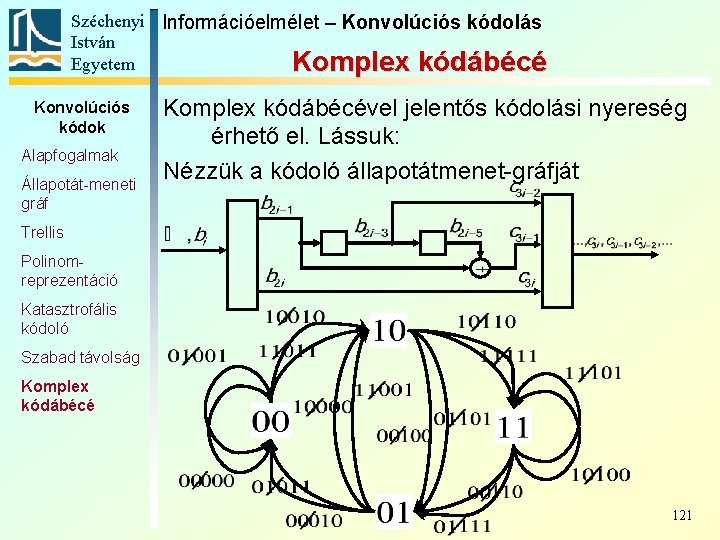
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Komplex kódábécé Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Komplex kódábécével jelentős kódolási nyereség érhető el. Lássuk: Nézzük a kódoló állapotátmenet-gráfját Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 121

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Komplex kódábécé Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Nézzük a kódoló trellisét: Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé 122

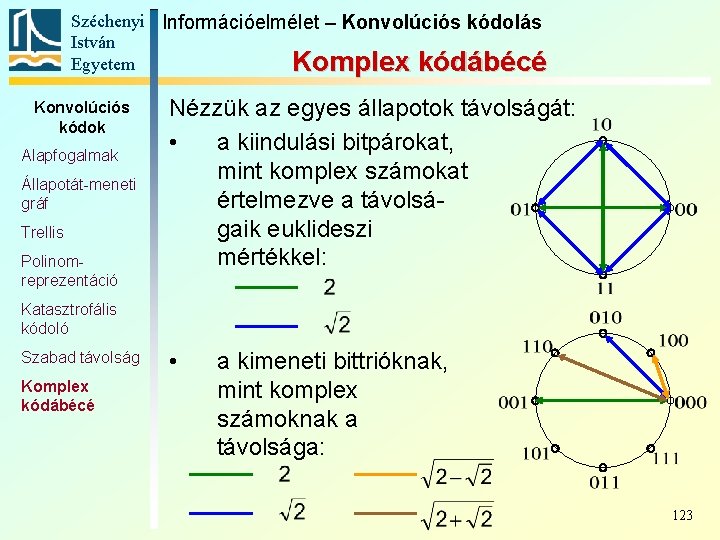
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Komplex kódábécé Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Nézzük az egyes állapotok távolságát: • a kiindulási bitpárokat, mint komplex számokat értelmezve a távolságaik euklideszi mértékkel: Katasztrofális kódoló Szabad távolság Komplex kódábécé • a kimeneti bittrióknak, mint komplex számoknak a távolsága: 123

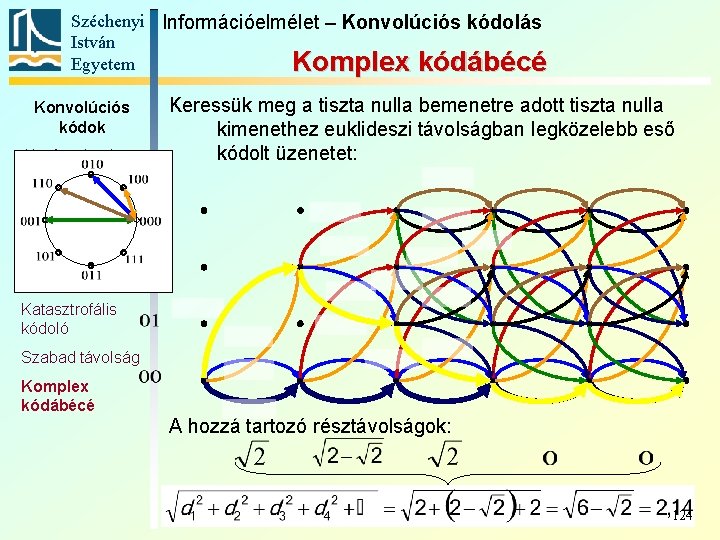
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Komplex kódábécé Konvolúciós kódok Alapfogalmak Keressük meg a tiszta nulla bemenetre adott tiszta nulla kimenethez euklideszi távolságban legközelebb eső kódolt üzenetet: Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé A hozzá tartozó résztávolságok: 124

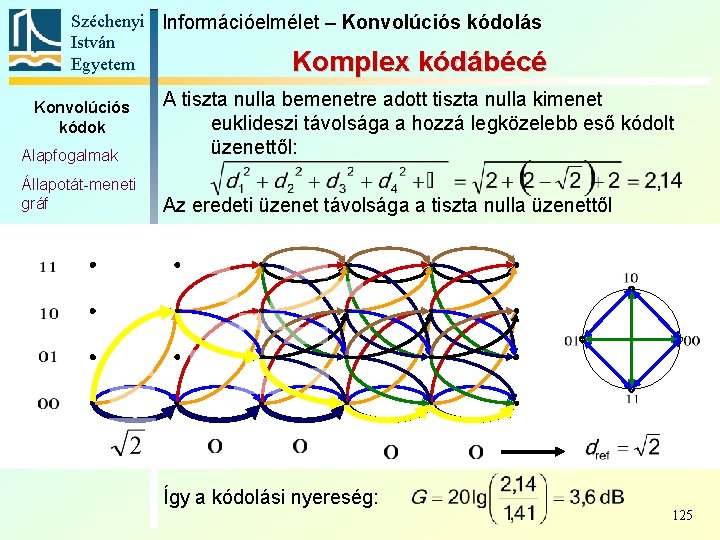
Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Komplex kódábécé Alapfogalmak A tiszta nulla bemenetre adott tiszta nulla kimenet euklideszi távolsága a hozzá legközelebb eső kódolt üzenettől: Állapotát-meneti gráf Az eredeti üzenet távolsága a tiszta nulla üzenettől Konvolúciós kódok Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé Így a kódolási nyereség: 125

Széchenyi Információelmélet – Konvolúciós kódolás István Egyetem Komplex kódábécé Konvolúciós kódok Alapfogalmak Állapotát-meneti gráf Trellis Polinomreprezentáció Katasztrofális kódoló Szabad távolság Komplex kódábécé A valós számokkal és Hamming-távolsággal ugyanez a kódolási nyereség: az üzenet: 10 00 00 … Hamming-távolsága a 00 00 00 … üzenettől: 1 kódolt üzenet: 010 100 010 000 Hamming-távolsága a 000 000 000 … kódolt üzenettől: 3 Így a kódolási nyereség: 126

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem Maximum likelihood dekódolás Viterbialgoritmus ML dekódolás Algoritmus Működés A Viterbi-dekódolás olyan algoritmus amelyet a trellis kódok maximum likelihood dekódolására fejlesztettek ki és optimalizáltak. Szemléltetés: Bináris szimmetrikus csatorna p < 1/2 paraméterrel. Legyen a csatornára adott vektor c = ( c 1 , c 2 , …, c N ), a kimeneten észlelt vektor v=( v 1 , v 2 , …, v N ). A p( v|c ) feltételes valószínűség: 127

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem Maximum likelihood dekódolás Viterbialgoritmus ML dekódolás Algoritmus Működés mivel a csatorna mindkét bit esetén 1−p valószínűséggel továbbít helyes jelet és p valószínűséggel hibáz; N darab szimbólum van és ebből d( v, c ) helyen tér el a két vektor egymástól, azaz ennyi helyen rontott a csatorna. 128

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem Maximum likelihood dekódolás Viterbialgoritmus Maximum likelihood döntésnél tehát a ML dekódolás Algoritmus Működés valószínűséget kell maximalizálni, azaz, mivel a d(v, c) Hamming-távolságot kell minimalizálni. 129

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem Maximum likelihood dekódolás Viterbialgoritmus ML dekódolás Algoritmus Működés Tehát a d(v, c) Hamming-távolságot kell minimalizálni. Jelöljük az i-edik kódszókeretet c i -vel, a belőle a csatorna kimenetén kapott szimbólumsorozatot v i -vel, távolságukat d(v i , c i )-vel. ekkor a Hamming-távolság minimumát kell keresni (d(c, v) a fenti szorzat kitevőjében van). 130

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem Maximum likelihood dekódolás Viterbialgoritmus ML dekódolás Algoritmus Működés A trellisben minden kódszókeretet egy-egy él reprezentál. Rendeljünk hozzá minden élhez egy olyan súlyfaktort avagy metrikát (mértéket), amely arányos ezzel a mennyiséggel, járjunk végig minden lehetséges utat, és válasszuk ki közülük a maximális súlyút. (Ha a Hamming-távolság a metrika akkor a minimumot kell keresni) Ez a Viterbi-dekódolás alapötlete. A legegyszerűbb, ha a vett bitsorozattól mért Hamming-távolságot nevezzük ki metrikának. (BSC esetén jó is) 131

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem Maximum likelihood dekódolás Viterbialgoritmus ML dekódolás Algoritmus Működés Más típusú diszkrét, emlékezet nélküli csatornánál is lehet a szorzatként előálló p(v|c) likelihood helyett olyan mennyiséget találni, amelyet egy-egy kódszókerethez tartozó részmennyiségek összegeként lehet meghatározni: 132

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem Az algoritmus Viterbialgoritmus ML dekódolás Algoritmus Működés A Viterbi-dekódolás A következő ciklust hajtja végre amíg el nem fogy a vett szimbólumsorozat: 1. beolvas egy kódszókeretet, az i-ediket: c i -t 2. kiszámolja a trellis i-edik és i+1 -edik mélységi csomópontjai közötti ágak súlyát a c i ismeretében 3. előhívja az i-edik mélységi csomópontokig vezető utak metrikáját, ezekhez hozzáadja az újakat, így minden i+1 -edik csomóponthoz kap több útvonalat különféle metrikával; 133

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem Az algoritmus Viterbialgoritmus 3. ML dekódolás Algoritmus Működés 4. előhívja az i-edik mélységi csomópontokig vezető utak metrikáját, ezekhez hozzáadja az újakat, így minden i+1 -edik csomóponthoz kap több útvonalat különféle metrikával; ezeket az útvonalakat hozzárendeli azokhoz az i+1 -edik mélységi csomópontokhoz, amelyekbe mutatnak. az állapotokhoz rendelt útvonalak közül kiválasztja a maximális súlyút, azt elraktározza az adott csomóponthoz, ez lesz a túlélő útvonal, a többit törli. (Hammingtávolság esetén a maximális súly a minimális Hamming-távolság. ) 134

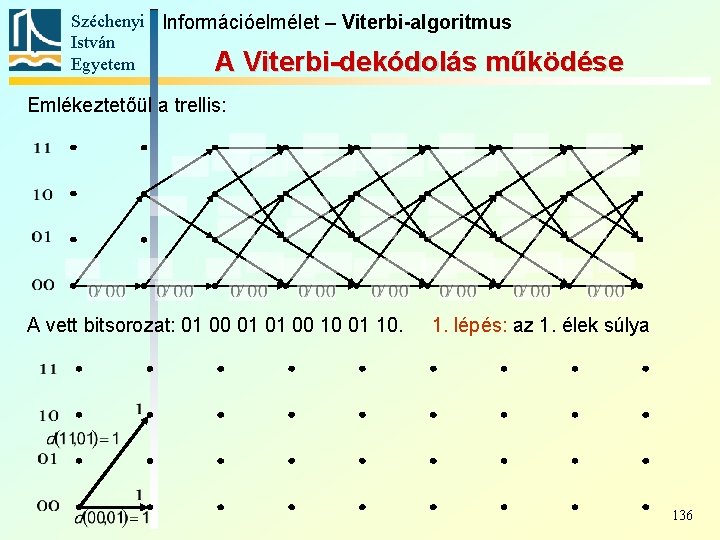
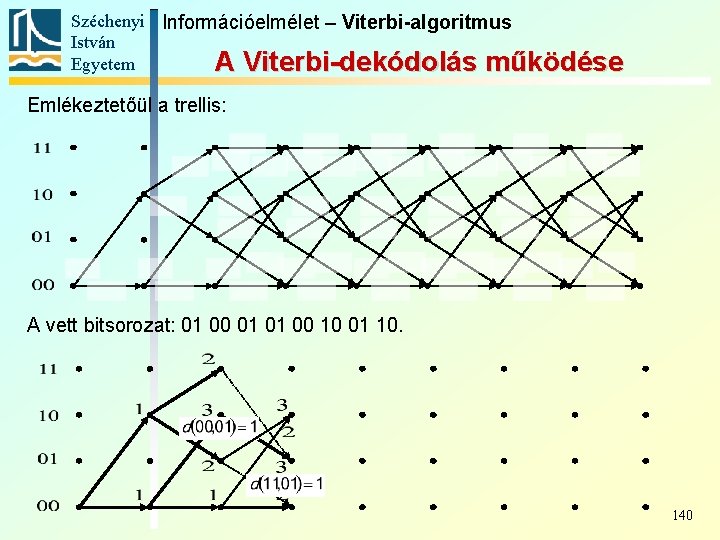
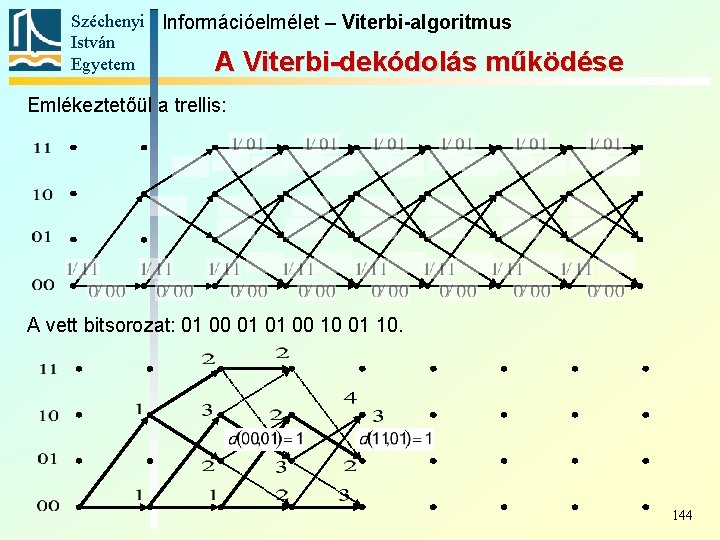
Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Nézzük az egyik egyszerű korábbi kódolónkat, és a belőle a 0 1 1 1 0 üzenet hatására kapott kódot: 00 00 11 01 00 10 01 10. Hibázzon a csatorna a második és az ötödik bitben, így a vett bitsorozat: 01 00 01 01 00 10 01 10. Hajtsuk végre a Viterbi-dekódolást: 135

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 1. lépés: az 1. élek súlya 136

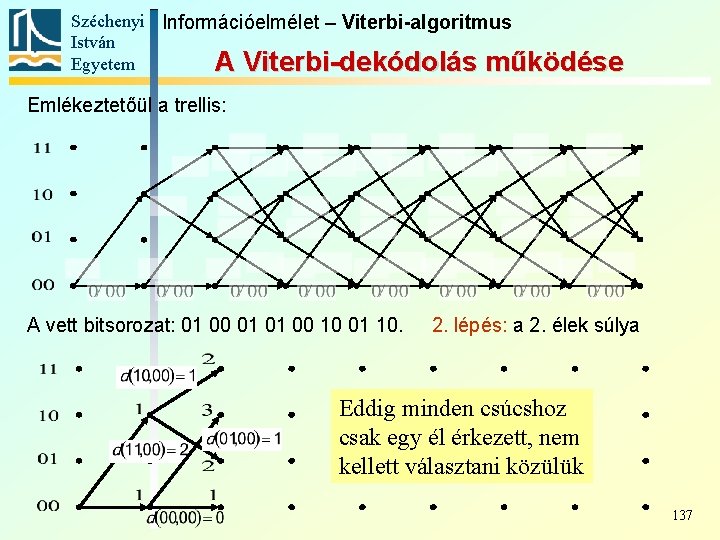
Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 2. lépés: a 2. élek súlya Eddig minden csúcshoz csak egy él érkezett, nem kellett választani közülük 137

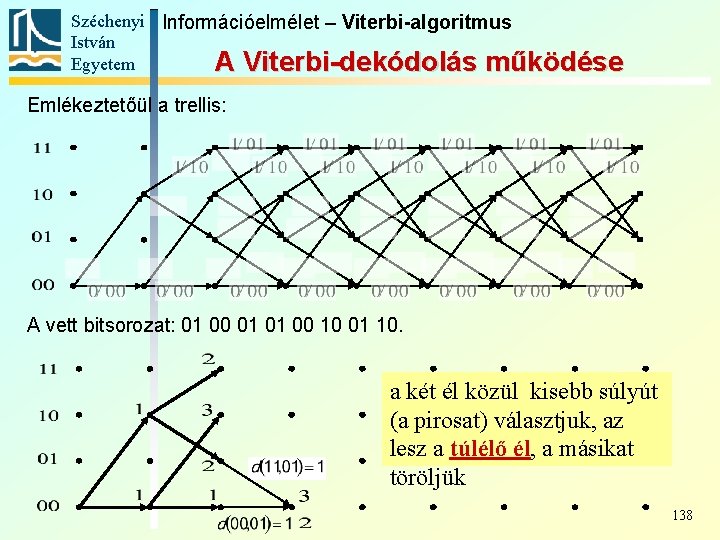
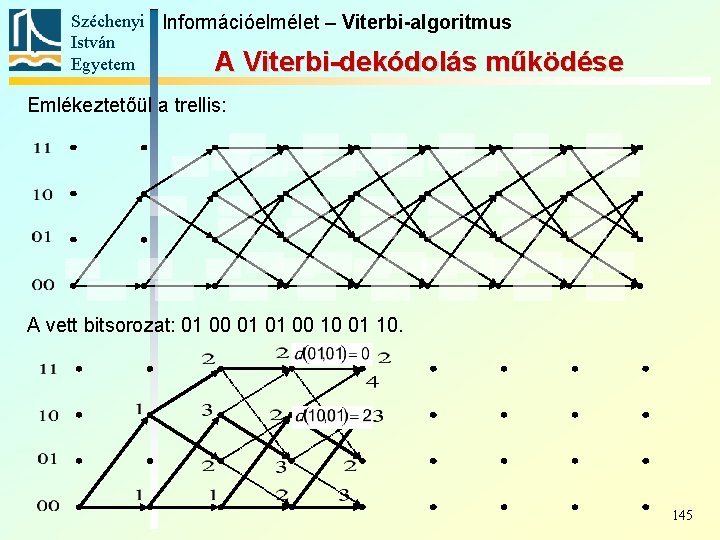
Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. a két él közül kisebb súlyút (a pirosat) választjuk, az lesz a túlélő él, a másikat töröljük 138

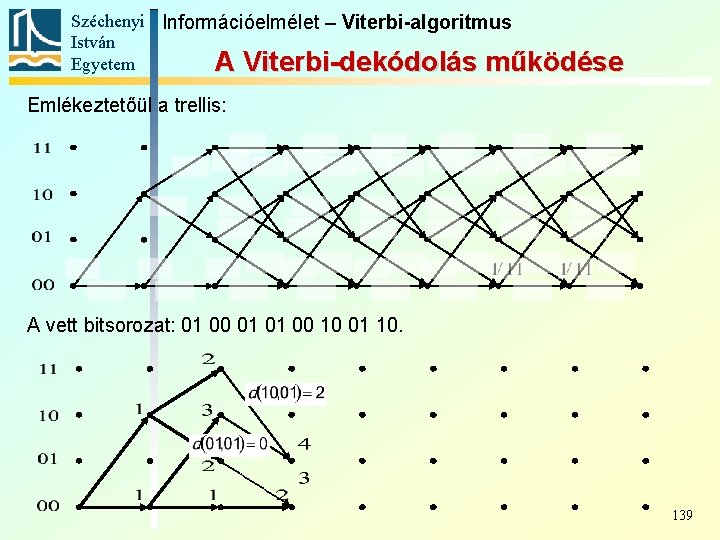
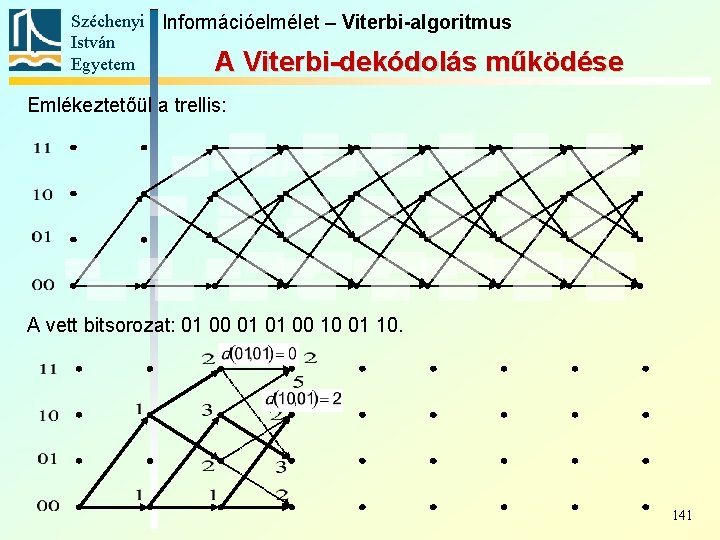
Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 139

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 140

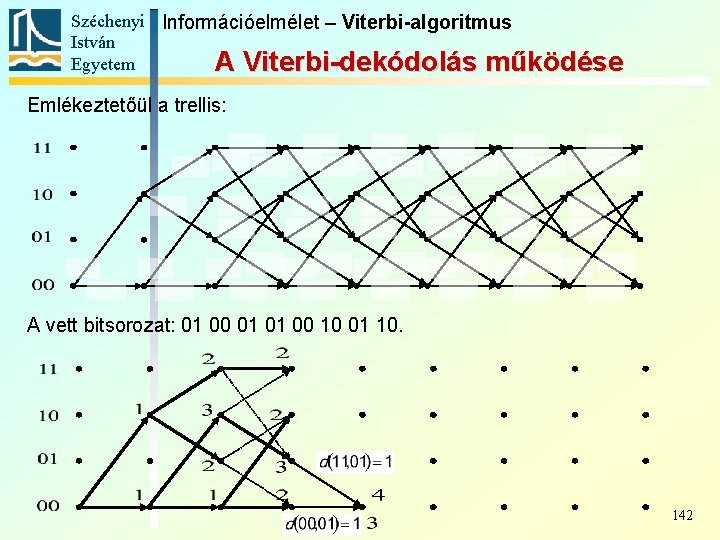
Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 141

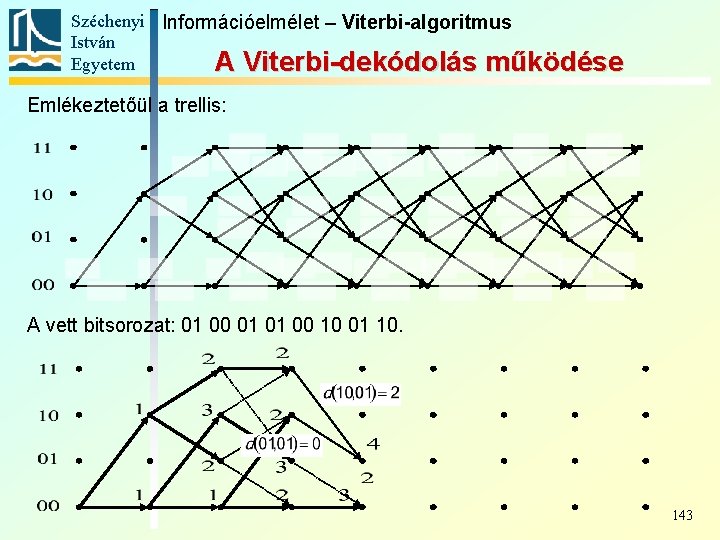
Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 142

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 143

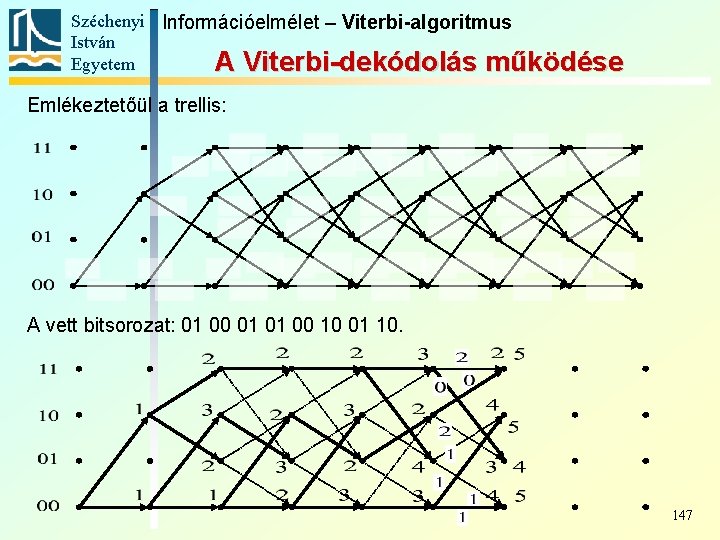
Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 144

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 145

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 146

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 147

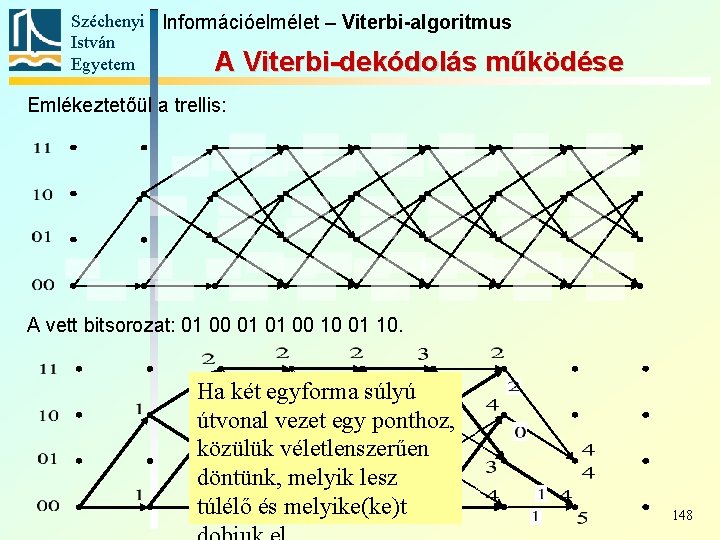
Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. Ha két egyforma súlyú útvonal vezet egy ponthoz, közülük véletlenszerűen döntünk, melyik lesz túlélő és melyike(ke)t 148

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 149

Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése Emlékeztetőül a trellis: A vett bitsorozat: 01 00 01 01 00 10 01 10. 150

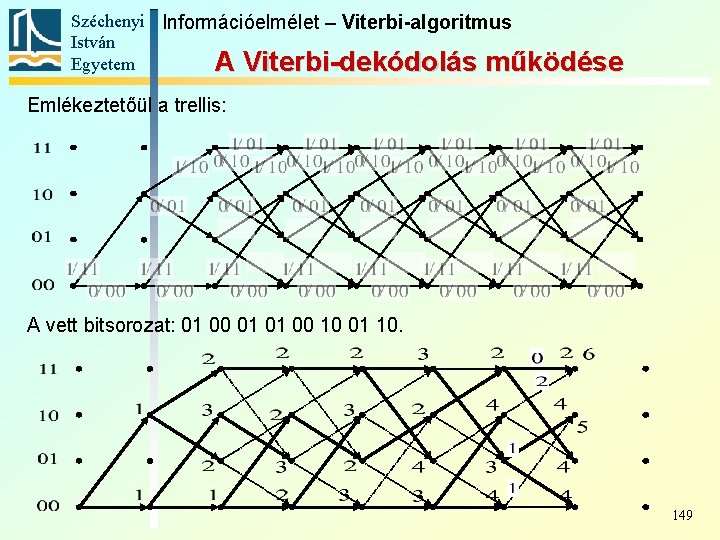
Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése A kapott túlélő útvonalak közül kiválasztjuk a minimális súlyút: a 2 súlyú utat. Az útvonal és a trellis ismeretében az üzenet visszakapható: 0 0 1 1 1 0 • Mivel minden pontba csak egy túlélő él fut be, a hibajavítás egyértelmű, a végétől visszafelé követhető az útvonal (fordított irányban vannak elágazások) 151

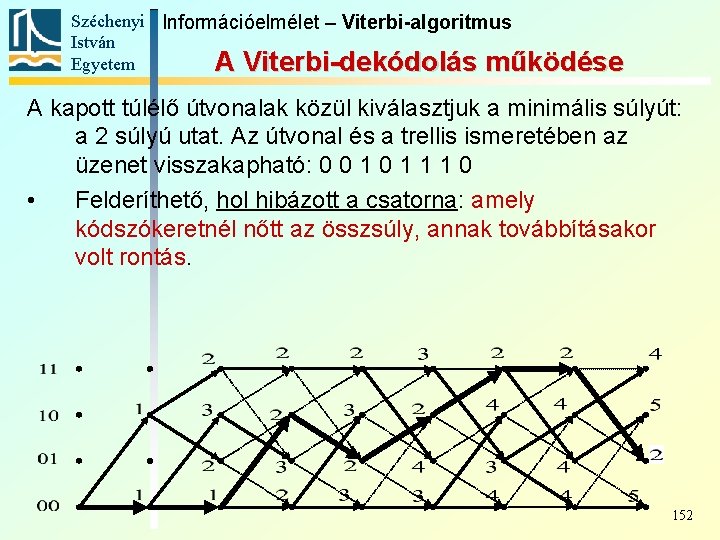
Széchenyi Információelmélet – Viterbi-algoritmus István Egyetem A Viterbi-dekódolás működése A kapott túlélő útvonalak közül kiválasztjuk a minimális súlyút: a 2 súlyú utat. Az útvonal és a trellis ismeretében az üzenet visszakapható: 0 0 1 1 1 0 • Felderíthető, hol hibázott a csatorna: amely kódszókeretnél nőtt az összsúly, annak továbbításakor volt rontás. 152

Széchenyi Információelmélet – Gyakorló feladatok István Egyetem Gyakorló feladatok: Konvolúciós kódolók Legyen egy k=1 -es konvolúciós kódolót jellemző két polinom: Rajzoljuk fel a kódoló blokkvázlatát! Adjuk meg a kódoló állapotátmeneti gráfját. 153

Széchenyi Információelmélet – Gyakorló feladatok István Egyetem Gyakorló feladatok: Konvolúciós kódolók Legyen egy k=1 -es konvolúciós kódolót jellemző állapotátmeneti gráf: Adjuk meg a kódoló trellisét a következő pontokat felhasználva. Adjuk meg a 0 1 1 0 üzenet által generált bitsorozatot tiszta nulla kezdeti tárolóállapotokat feltéve. Mi marad a végén a tárolókban? 154

Széchenyi Információelmélet – Gyakorló feladatok István Gyakorló feladatok: Viterbi Egyetem algoritmus Az alábbi trellis alapján dekódoljuk az 11 01 00 11 01 10 00 vett bitsorozatot! Mennyi hiba történt a csatornán és mely pozíciókban? 155