Informcielmlet Nagy Szilvia 11 A ReedSolomonkdok spektruma s

Információelmélet Nagy Szilvia 11. A Reed—Solomon-kódok spektruma és dekódolása 2005.

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Fourier-transzformálás véges testeken Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció Legyen a c=(c 0 , c 1 , …, c n− 1 ) GF(NM )-beli n komponensű vektor C =(C 0 , C 1 , …, C n− 1 ) (GF(NM ))n Fouriertranszformáltjának komponensei a A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása képlet szerint állnak elő, J a véges test nedrendű eleme. Szokás a C Fourier-transzformáltat F {c}-ként írni és a c spektrumának nevezni. 2

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Fourier-transzformálás véges testeken Reed— Solomon-kódok II. Fouriertranszformáció Példa: számoljuk ki a c=(3 0 1 4) GF(5 )-beli 4 komponensű vektor Fourier-transzformáltjának komponenseit J =3 -mal: Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 3

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Fourier-transzformálás véges testeken Reed— Solomon-kódok II. A Fourier-transzformációnak van inverz művelete: Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása ahol n− 1 az n-nek a GF(N M) véges testen belüli inverze. Bináris esetben, azaz ha N=2, n− 1=1 (ha n páratlan). Egyszerű hibák javítása 4

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. Fouriertranszformáció Legyen a t=(t 0 , t 1 , …, t n− 1 ) és u=(u 0 , u 1 , …, u M n− 1 ) két GF(N )-beli n komponensű vektor. Az s=t u ciklikus konvolúciója az az s =(s M n 0 , s 1 , …, s n− 1 ) (GF(N )) vektor, melynek komponensei: Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A ciklikus konvolúcióra érvényes a konvolúciós tétel: Ha az s, t, u vektorok Fouriertranszformáltjai rendre S, T, U, és a vektorok komponensei között fennáll, hogy akkor a spektrum vektorokra igaz, hogy 5

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. A konvolúciós tétel belátása: az s vektorok Fourier-transzformáltjának, S-nek az i-edik komponense Fouriertranszformáció Konvolúció A spektrum jellemzői behelyettesítve u-t, mint U-nak az inverz. Fourier-transzformáltját Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása ha j−k<0, akkor az nnel vett osztás utáni maradékát kell venni 6

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. Példa: adjuk meg az a=(3 0 1 4) és a b=(2 0 2 1) vektorok konvolúcióját GF(5) felett. (n=4, 4− 1≡ 4 mod 5. ) Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 7

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. Fouriertranszformáció Legyen J a GF(NM )test n-edrendű eleme. Egy c (GF(NM ))n vektor spektrum-polinomja a C=(C 0 , C 1 , …, C n− 1 ) spektrumához rendelt legfeljebb n− 1 -edfokú polinom: Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 8

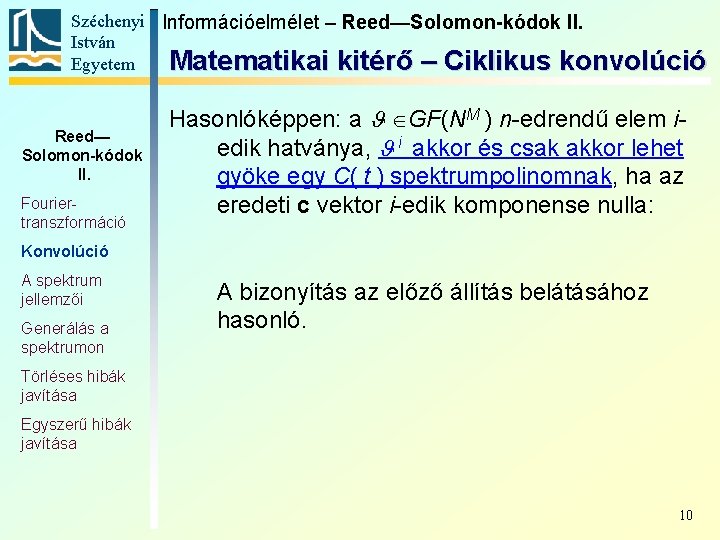
Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői A J GF(NM ) n-edrendű elem i-edik hatványa, J i akkor és csak akkor lehet gyöke egy c( t ) polinomnak, ha a polinomhoz tartozó vektor C spektrumában az i-edik elem nulla: Bizonyítás: ha J i gyöke c(t)-nek, akkor c(J i) = 0. Kifejtve: Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása ami pont C i. 9

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Matematikai kitérő – Ciklikus konvolúció Reed— Solomon-kódok II. Fouriertranszformáció Hasonlóképpen: a J GF(NM ) n-edrendű elem iedik hatványa, J i akkor és csak akkor lehet gyöke egy C( t ) spektrumpolinomnak, ha az eredeti c vektor i-edik komponense nulla: Konvolúció A spektrum jellemzői Generálás a spektrumon A bizonyítás az előző állítás belátásához hasonló. Törléses hibák javítása Egyszerű hibák javítása 10

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem A Reed—Solomon-kódok spektruma Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Legyen a Reed—Solomon-kód generátorpolinomja g( t ), a kódolandó üzenet polinomja b( t ), a hozzárendelt kódszópolinom c( t ). A c( t ) n− 1 -edfokú, b( t ) k− 1 -edfokú, g( t ) pedig n−k− 1 -edfokú. Az n− 1 -edfokú polinomok között a b( t )-nek és g( t )-nek az utolsó együtthatói nullák. Mindhárom polinom származtatható n komponensű vektorokból is: Törléses hibák javítása Egyszerű hibák javítása 11

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem A Reed—Solomon-kódok spektruma Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A Reed—Solomon-kód c( t ) kódszópolinomjai a következőképpen állíthatók elő: A polinomszorzás definíciója szerint az i-edfokú együttható: A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása ami g b i-edik komponense. Tehát c = g b. A konvolúciós tétel szerint ekkor a vektorok spektruma között a következő összefüggés áll fenn: 12

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem A Reed—Solomon-kódok spektruma Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Legyen a Reed—Solomon-kódot generáló és egyben a Fourier- transzformációt definiáló n -edrendű GF(NM )-beli elem J. A generátorpolinomnak, s így minden kódszópolinomnak gyöke J 1 -től n – kadikig terjedő hatványa. Így minden kódszóvektor spektrumának az 1 -től n – k-adikig terjedő indexű komponense nulla: Egyszerű hibák javítása 13

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem A Reed—Solomon-kódok spektruma Reed— Solomon-kódok II. Minden kódszóvektor spektrumának az 1 -től n – k-adikig terjedő indexű komponense nulla: Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása Ez a tény lehetővé teszi a kódszavak spektrumukon keresztül történő definiálását: a (b 0 , b 1 , …, b k− 1) üzenethez rendelt kódszó spektrumának – az első n−k eleme 0 – az utolsó k eleme b 0 , b 1 , …, b k− 1 14

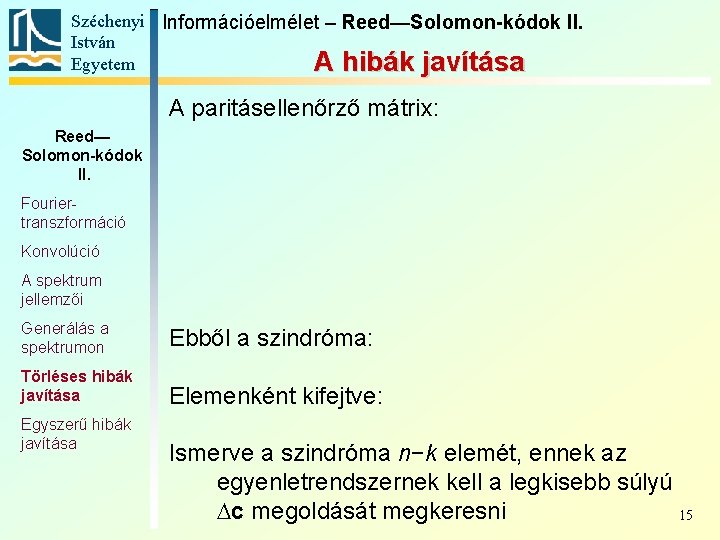
Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem A hibák javítása A paritásellenőrző mátrix: Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Ebből a szindróma: Törléses hibák javítása Elemenként kifejtve: Egyszerű hibák javítása Ismerve a szindróma n−k elemét, ennek az egyenletrendszernek kell a legkisebb súlyú Dc megoldását megkeresni 15

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Törléses hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása Törléses hibák esetén ismerjük azt, hogy Dc mely komponensei biztosan 0 -k és melyek nem azok. A 0 elemek a HT bármely oszlopával összeszorozva 0 járulékot adnak, így a velük azonos sorszámú sorokat törölhetjük HT-ből. Összesen legfeljebb n−k nem nulla elem van Dcben, így legfeljebb n−k sora marad a csonkolt HT-nek. Eleve csak n−k oszlopa volt, így négyzetes mátrix marad. Legyen a csonkolt paritásellenőrző mátrix Húzzuk ki Dc-ből is a 0 elemeket, az így kapott vektor: 16

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Törléses hibák javítása A kapott Reed— Solomon-kódok II. Fouriertranszformáció avagy Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása n−k változós egyenletrendszer megoldható. 17

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció A Reed—Solomon-kódok n <(n−k)/2 egyszerű hibát tudnak javítani. Tegyük fel, hogy az ℓ-edik helyen van hiba. Ekkor minden Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása egyenletben szerepel egy-egy nem 0 tag: J ℓ-ből egyértelműen megadható a hiba helye, csak meg kell keresni, hogy hányadik hatványa J -nak. A J ℓ mennyiség a hibahely-lokátor 18

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Legyen Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása a hibahely-polinom, melynek gyökei a hibahelylokátorok inverzei. Ha meg tudjuk határozni L(t)-t, akkor • a gyökeit ki tudjuk számolni • meg tudjuk adni a gyökök inverzét, azaz a hibahely-lokátorokat • meg tudjuk keresni, hogy azok J hányadik hatványai, azaz meg tudjuk adni, hol vannak hibák Ha a hibák helyét ismerjük, akkor törléses hibákat kell javítani, azt meg láttuk hogyan kell. 19

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása L-re igaz, hogy Reed— Solomon-kódok II. Fouriertranszformáció Szorozzuk mindkét oldalt Konvolúció A spektrum jellemzői Összegezzünk ℓ=1, 2, …, n –re Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása Helyettesítsük be L(t)=1+L 1 t+…+Ln tn polinom egyelőre ismeretlen együtthatóit: 20

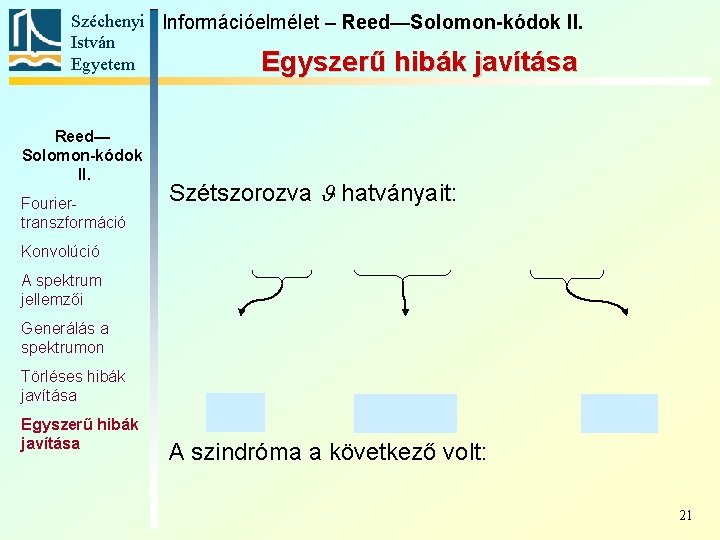
Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Szétszorozva J hatványait: Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A szindróma a következő volt: 21

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Így kaptunk egyenletrendszert L(t) együtthatóira, amelyben csak a szindróma szerepel: Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása ahol j lehet 0, 1, …, n. A szindróma legmagasabb indexszel a j+n -vel fordul elő az egyenletrendszerben, ami legfeljebb 2 n lehet, ami nem haladja meg s komponenseinek a számát. (Hiszen legfeljebb (n−k)/2 egyszerű hiba javítható, a szindróma meg n−k komponensű. ) Az egyenletrendszer tehát mindig felírható. 22

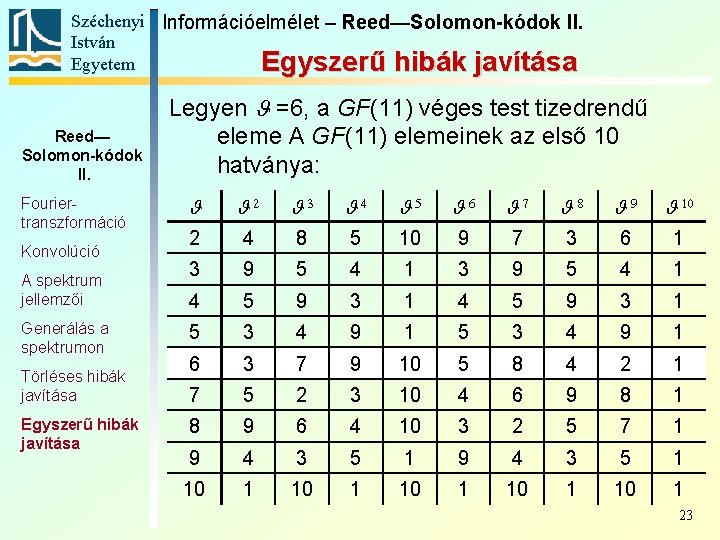
Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása Legyen J =6, a GF(11) véges test tizedrendű eleme A GF(11) elemeinek az első 10 hatványa: J J 2 J 3 J 4 J 5 J 6 J 7 J 8 J 9 J 10 2 4 8 5 10 9 7 3 6 1 3 9 5 4 1 4 5 9 3 1 5 3 4 9 1 6 3 7 9 10 5 8 4 2 1 7 5 2 3 10 4 6 9 8 1 8 9 6 4 10 3 2 5 7 1 9 4 3 5 1 10 1 10 1 23

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Legyen J =6, a GF(11) véges test feletti (10, 6) paraméterű Reed—Solomon-kód generáló eleme. A generátormátrix: Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A (0 2 6 7 1 1) üzenet által létrehozott kódszó: 24

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Legyen J =6, a GF(11) véges test feletti (10, 6) paraméterű Reed—Solomon-kód generáló eleme. A paritásellenőrző mátrix: Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A (6 10 7 5 0 8 0 5 6 0) vett vektorból kapott szindróma: (233 108 230 141)≡ ≡(2 9 10 9). 25

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Dekódoljuk a J =6 generáló elemű, GF(11) feletti (10, 6) Reed—Solomon-kód kódszavából torzult (6 10 7 5 0 8 0 5 6 0) vektort. A szindróma: (2 9 10 9). Konvolúció A spektrum jellemzői alkalmazása j=0 és 1 -re: Generálás a spektrumon Törléses hibák javítása azaz Egyszerű hibák javítása 26

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Dekódoljuk a J =6 generáló elemű, GF(11) feletti (10, 6) Reed—Solomon-kód kódszavából torzult (6 10 7 5 0 8 0 5 6 0) vektort. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 27

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Dekódoljuk a J =6 generáló elemű, GF(11) feletti (10, 6) Reed—Solomon-kód kódszavából torzult (6 10 7 5 0 8 0 5 6 0) vektort. A hibahelypolinom: Konvolúció A spektrum jellemzői Generálás a spektrumon Gyökei: 4 és 5: Törléses hibák javítása Egyszerű hibák javítása Inverzeik: 28

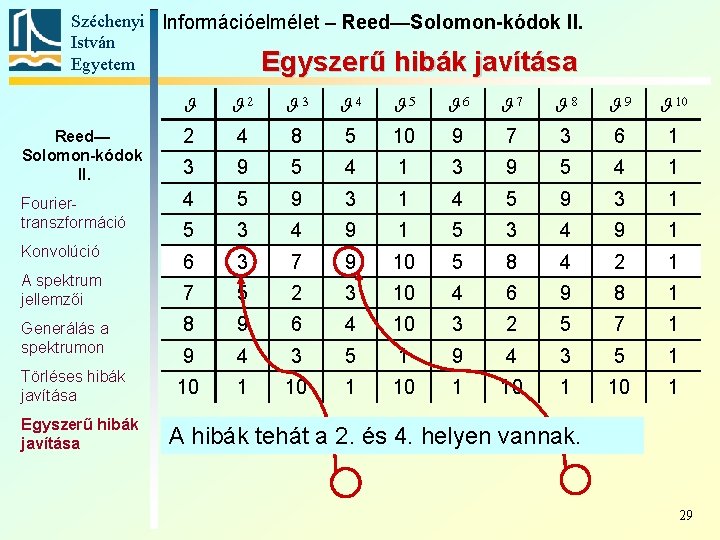
Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása J J 2 J 3 J 4 J 5 J 6 J 7 J 8 J 9 J 10 Reed— Solomon-kódok II. 2 4 8 5 10 9 7 3 6 1 3 9 5 4 1 Fouriertranszformáció 4 5 9 3 1 5 3 4 9 1 6 3 7 9 10 5 8 4 2 1 7 5 2 3 10 4 6 9 8 1 8 9 6 4 10 3 2 5 7 1 9 4 3 5 1 10 1 10 1 Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A hibák tehát a 2. és 4. helyen vannak. 29

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A hibák tehát a 2. és 4. helyen vannak. A csonkolt paritásellenőrző mátrix: A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 30

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon A hibák tehát a 2. és 4. helyen vannak. A csonkolt paritásellenőrző mátrix: A csonkolt hibavektor: A szindróma (2 9 10 9) volt, Törléses hibák javítása Egyszerű hibák javítása 31

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon A hibák tehát a 2. és 4. helyen vannak. A csonkolt paritásellenőrző mátrix: A csonkolt hibavektor: A szindróma (2 9 10 9) volt, Törléses hibák javítása Egyszerű hibák javítása 32

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Behelyettesítés után: Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása 33

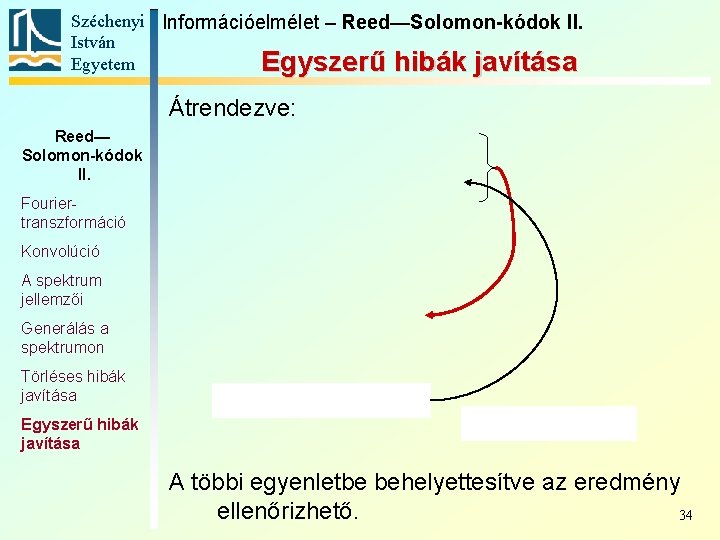
Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Átrendezve: Reed— Solomon-kódok II. Fouriertranszformáció Konvolúció A spektrum jellemzői Generálás a spektrumon Törléses hibák javítása Egyszerű hibák javítása A többi egyenletbe behelyettesítve az eredmény ellenőrizhető. 34

Széchenyi Információelmélet – Reed—Solomon-kódok II. István Egyetem Egyszerű hibák javítása Reed— Solomon-kódok II. Fouriertranszformáció Dekódoljuk a J =6 generáló elemű, GF(11) feletti (10, 6) Reed—Solomon-kód kódszavából torzult (6 10 7 5 0 8 0 5 6 0) vektort. A hibavektor komponensei: Konvolúció A spektrum jellemzői Generálás a spektrumon A javított kódszó: Törléses hibák javítása (6 10 1 5 3 8 0 5 6 0) Egyszerű hibák javítása 35