INF 2310 18 05 2011 En enkelttime Mesteparten

INF 2310 – 18. 05. 2011 | En enkelttime Mesteparten av kap 9. 1 -9. 5 i DIP Morfologiske operasjoner på binære bilder q Basis-begreper q Fundamentale operasjoner på binære bilder q Sammensatte operasjoner q Eksempler på anvendelser flettet inn 18. 05. 2011 1 / 38

Introduksjon q Analyse av bilder og objekter basert på form (shape) q Modifiserer former ved lokale operatorer basert på set-teori q Mange benyttes til å fjerne uønskede effekter etter segmentering § Fjerning av små objekter (støy-objekter) § Glatting av omrisset til større objekter § Fjerning av hull i objekter § Lenke sammen objekter q Noen operatorer er nyttige til analyse og beskrivelse av objekter § Finne omriss av objekter § Objektskjeletter § Finne objekter som inneholder en viss struktur § Finne fordelingen av størrelsen på objektene § Finne fordelingen av størrelsen på mellomrommene mellom objektene § Finne mønstre i bilder q Operasjonene er ofte enkle og kan utføres svært raskt 18. 05. 2011 2 / 38

Eksempel q Her vil morfologiske operatorer være velegnet til å prosessere formen på de segmenterte tallene etter terskling, men før gjenkjenning. En del små støy-objekter. Noen symboler er fragmentert i flere deler. Kanten rundt noen symboler kan være rufsete. 18. 05. 2011 3 / 38

Litt sett-teori q La A være et sett i Z 2. Dersom punktet a=(a 1, a 2) er et element i A skriver vi: q Dersom a ikke er inneholdt i A skriver vi: q Settet uten noen elementer kalles det tomme settet og betegnes q Elementene som ikke er i A kalles komplementet til A, og betegnes Ac q Dersom alle elementene i A er inneholdt i B sies A å være et subsett av B, dette skrives: q Med unionen av to sett A og B mener vi settet som består av alle elementer fra enten A eller B, dette betegnes: q Med snittet av A og B mener vi settet som består av elle elementer som finnes i både A og B, dette betegnes: 18. 05. 2011 4 / 38

Litt sett-teori i praksis på binære bilder q Komplementet til et binært bilde f, q Snittet av to bilder f og g q Unionen av to bilder f og g 18. 05. 2011 5 / 38

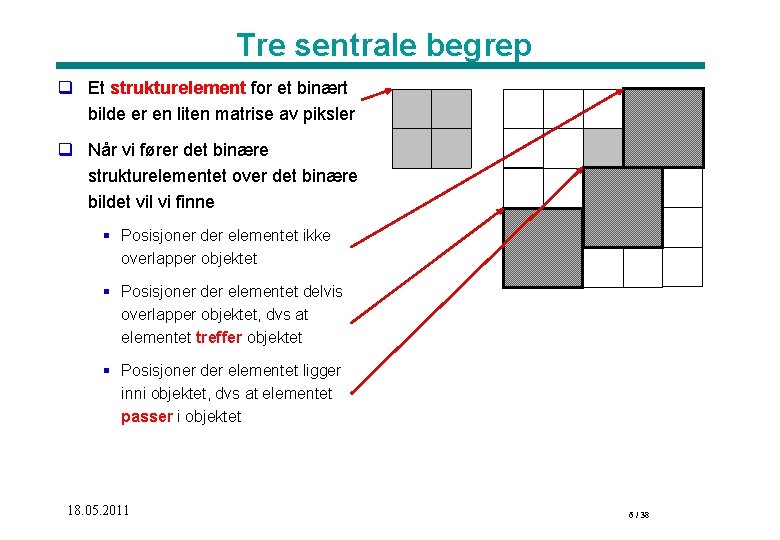
Tre sentrale begrep q Et strukturelement for et binært bilde er en liten matrise av piksler q Når vi fører det binære strukturelementet over det binære bildet vil vi finne § Posisjoner der elementet ikke overlapper objektet § Posisjoner der elementet delvis overlapper objektet, dvs at elementet treffer objektet § Posisjoner der elementet ligger inni objektet, dvs at elementet passer i objektet 18. 05. 2011 6 / 38

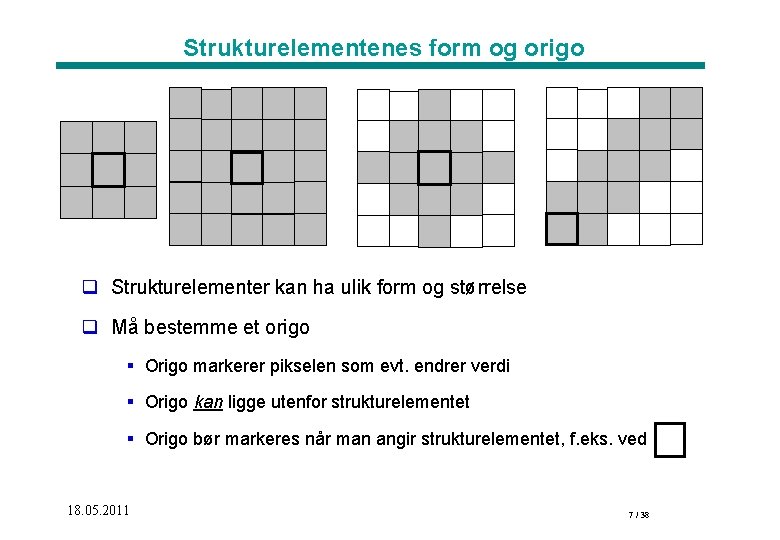
Strukturelementenes form og origo q Strukturelementer kan ha ulik form og størrelse q Må bestemme et origo § Origo markerer pikselen som evt. endrer verdi § Origo kan ligge utenfor strukturelementet § Origo bør markeres når man angir strukturelementet, f. eks. ved 18. 05. 2011 7 / 38

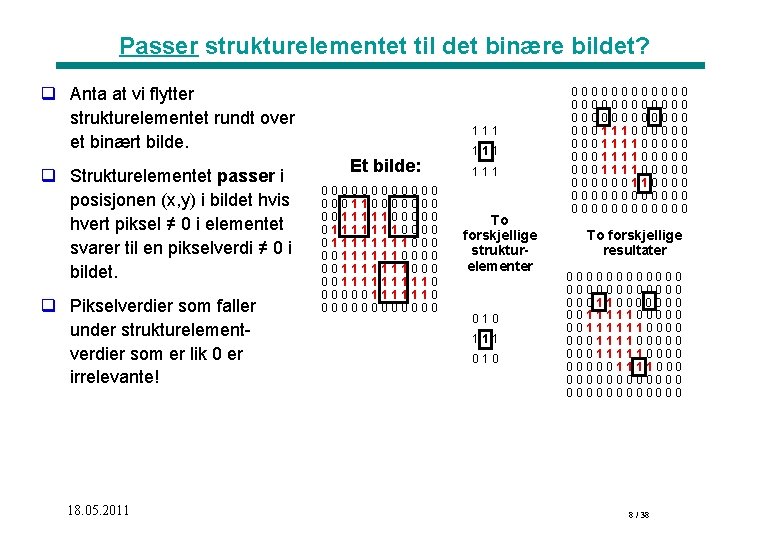
Passer strukturelementet til det binære bildet? q Anta at vi flytter strukturelementet rundt over et binært bilde. q Strukturelementet passer i posisjonen (x, y) i bildet hvis hvert piksel ≠ 0 i elementet svarer til en pikselverdi ≠ 0 i bildet. q Pikselverdier som faller under strukturelementverdier som er lik 0 er irrelevante! 18. 05. 2011 111 Et bilde: 000000 000110000000 001111100000 011111111000 001111110000 001111111110 000001111110 000000 111 To forskjellige strukturelementer 010 111 010 000000000000 000111000000 000111100000 00000011000000000000 To forskjellige resultater 000000000000 000110000000 001111110000 000111100000 00011111000001111000 000000000000 8 / 38

Erosjon q Plasser strukturelementet S slik at origo ligger over bildet f med koordinatene (x, y), og bruk regelen q Erosjon av et bilde f med strukturelementet S betegnes 01000001100 111000111100 00111111000 00011111100 001111000111 00110000010 erodert med 111 010 111 q Mer presist: Erosjonen av et sett X med strukturelementet S er definert som posisjonen til alle piksler x slik at S er inkludert i X når origo i S plasseres i x: 18. 05. 2011 gir 00000000000 0000001000000 00000000000 gir 000000 01000001100 00100011000 000101100001101000 00011000100 00110000010 000000 9 / 38

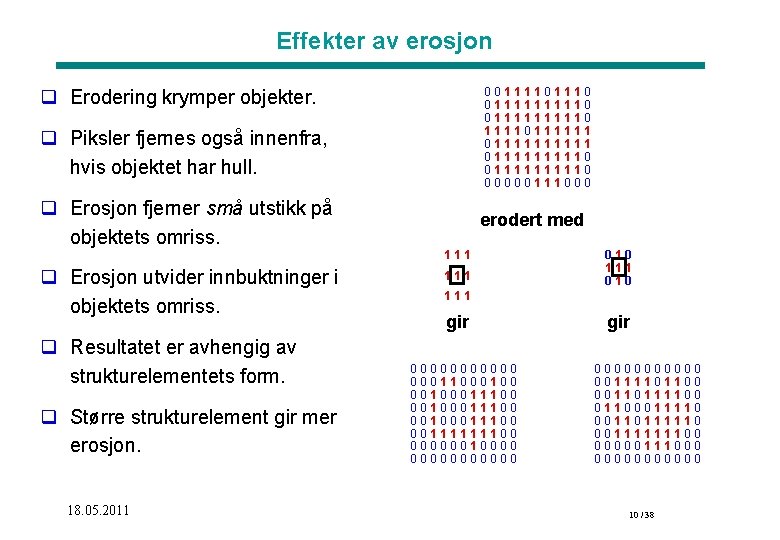
Effekter av erosjon 0011110 01111111110111111 01111111110 0111110 00000111000 q Erodering krymper objekter. q Piksler fjernes også innenfra, hvis objektet har hull. q Erosjon fjerner små utstikk på objektets omriss. erodert med 111 q Erosjon utvider innbuktninger i objektets omriss. q Resultatet er avhengig av strukturelementets form. q Større strukturelement gir mer erosjon. 18. 05. 2011 111 010 111 gir 000000 00011000100011100 00100011100 00111111100 0000001000000 gir 000000 00111101100 00110111100 01100011110 00110111110 00111111100 00000111000 000000 10 / 38

Iterativ erosjon 0011110 01111111110111111 01111111110 0111110 00000111000 q Større strukturelement gir mer erosjon. q Resultatet av erosjon med et stort strukturelement er (nesten) lik resultatet av gjentatt erosjon med et mindre element med samme form. q Hvis s 2 er formlik s 1, men dobbelt så stort, så er f ө s 2 ≈ (f ө s 1) ө s 1 18. 05. 2011 erodert 2 ganger med 111 010 111 gir 00000000000 00000001000 00000000000 gir 000000000001000 00000001100 000000111000 00000000000 11 / 38

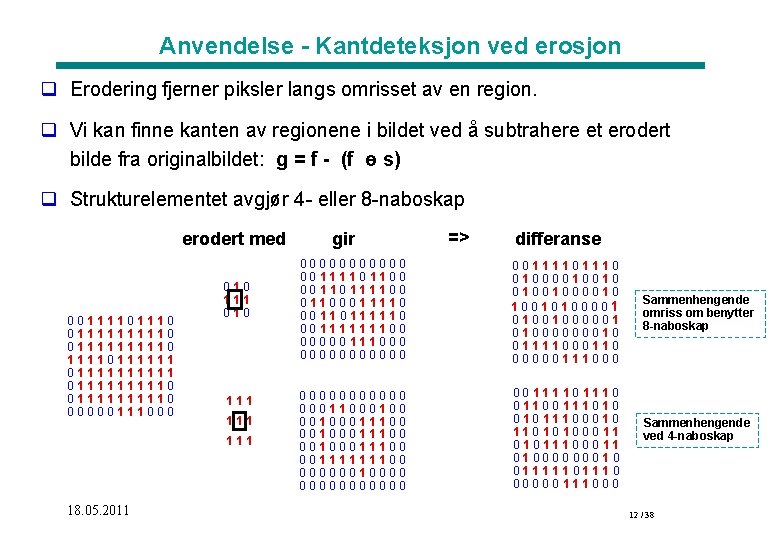
Anvendelse - Kantdeteksjon ved erosjon q Erodering fjerner piksler langs omrisset av en region. q Vi kan finne kanten av regionene i bildet ved å subtrahere et erodert bilde fra originalbildet: g = f - (f ө s) q Strukturelementet avgjør 4 - eller 8 -naboskap erodert med 0011110 01111111110111111 01111111110 0111110 00000111000 010 111 111 18. 05. 2011 gir => differanse 000000 00111101100 00110111100 01100011110 00110111110 00111111100 00000111000 000000 0011110 0100001001000010 10010100001 01001000001 01000000010 01111000110 00000111000 000000 00011000100011100 00100011100 00111111100 0000001000000 0011110 01100111010 01011100010 11010100011 01011100011 01000000010 0111110 00000111000 Sammenhengende omriss om benytter 8 -naboskap Sammenhengende ved 4 -naboskap 12 / 38

Eksempel – Kantdeteksjon ved erosjon / omriss 010 111 111 18. 05. 2011 13 / 38

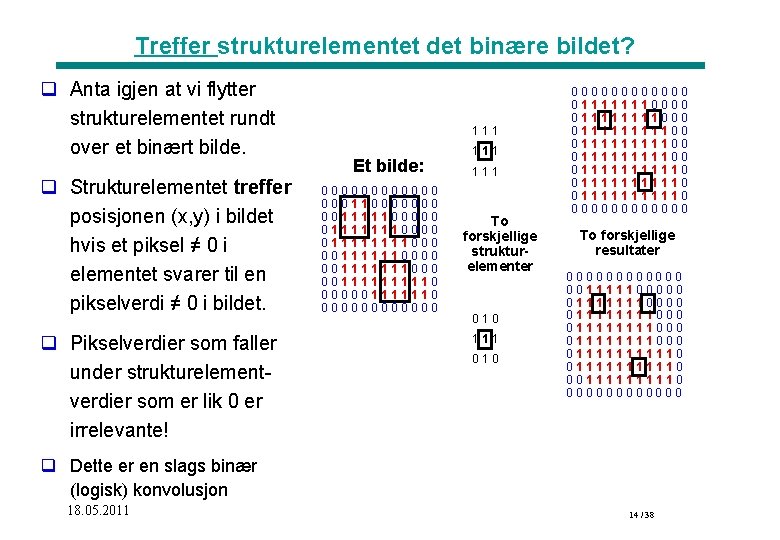
Treffer strukturelementet det binære bildet? q Anta igjen at vi flytter strukturelementet rundt over et binært bilde. q Strukturelementet treffer posisjonen (x, y) i bildet hvis et piksel ≠ 0 i elementet svarer til en pikselverdi ≠ 0 i bildet. q Pikselverdier som faller under strukturelementverdier som er lik 0 er irrelevante! 111 Et bilde: 000000 000110000000 001111100000 011111111000 001111110000 001111111110 000001111110 000000 111 To forskjellige strukturelementer 010 111 010 000000 011111110000 011111111100 011111111110 0111110 000000 To forskjellige resultater 000000 001111100000 011111111000 011111111110 00111110 000000 q Dette er en slags binær (logisk) konvolusjon 18. 05. 2011 14 / 38

Dilasjon (dilatasjon, eng: dilation) q Plasser S slik at origo ligger i (x, y), og bruk regelen 000000 01000001100 00100011000 000101100001101000 00011000100 00110000010 000000 dilatert med q Dilasjon av et bilde f med strukturelementet S betegnes 111 010 111 q Mer presist: Dilasjonen av et sett X med strukturelementet S er definert som posisjonen til alle piksler x slik at S overlapper med X i minst ett piksel når origo i S plasseres i x: 18. 05. 2011 gir 000000 0111110 01111111100 00111111110 0111110 00000000000 011000111100 00111111000 00011111100 0011110 00111000110 000000 15 / 38

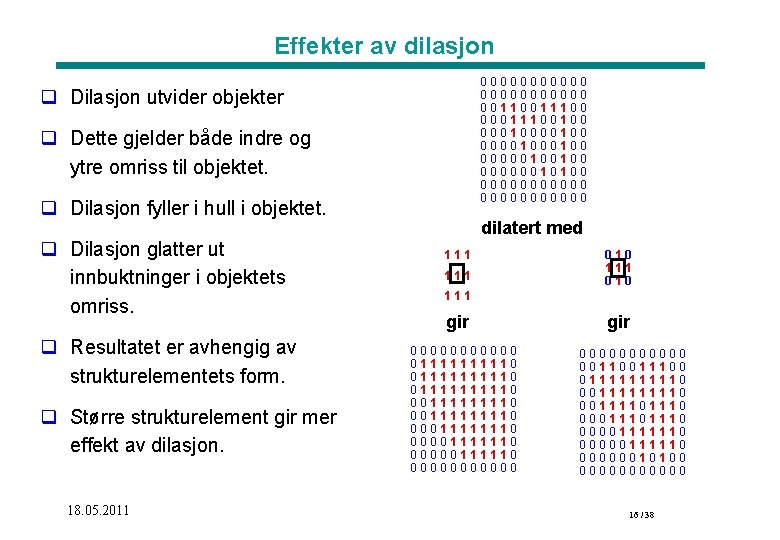
Effekter av dilasjon 00000000000 0011100 00011100100 000100 0000100 00000100100 00000010100 00000000000 q Dilasjon utvider objekter q Dette gjelder både indre og ytre omriss til objektet. q Dilasjon fyller i hull i objektet. q Dilasjon glatter ut innbuktninger i objektets omriss. q Resultatet er avhengig av strukturelementets form. q Større strukturelement gir mer effekt av dilasjon. 18. 05. 2011 dilatert med 111 010 111 gir 000000 01111111110 0111110 00111111110 00011111110 00000111110 000000 gir 000000 0011100 0111110 00111101110 00001111110 00000010100 000000 16 / 38

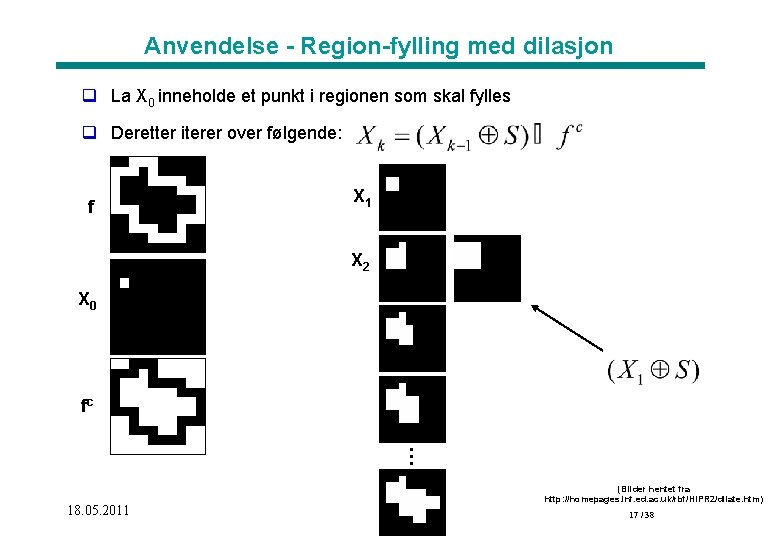
Anvendelse - Region-fylling med dilasjon q La X 0 inneholde et punkt i regionen som skal fylles q Deretter iterer over følgende: f X 1 X 2 X 0 fc … 18. 05. 2011 (Bilder hentet fra http: //homepages. inf. ed. ac. uk/rbf/HIPR 2/dilate. htm) 17 / 38

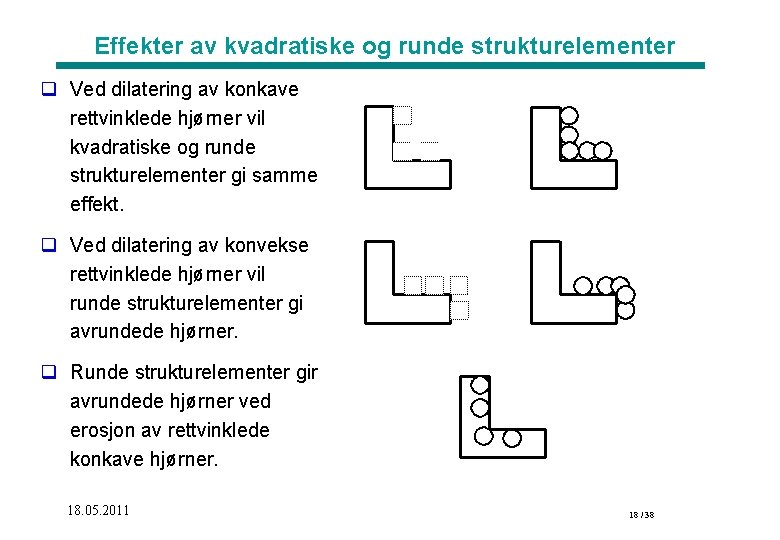
Effekter av kvadratiske og runde strukturelementer q Ved dilatering av konkave rettvinklede hjørner vil kvadratiske og runde strukturelementer gi samme effekt. q Ved dilatering av konvekse rettvinklede hjørner vil runde strukturelementer gi avrundede hjørner. q Runde strukturelementer gir avrundede hjørner ved erosjon av rettvinklede konkave hjørner. 18. 05. 2011 18 / 38

Dualitet q Dilasjon og erosjon er duale, dvs operasjonene har motsatt effekt, eller de kan uttrykkes ved hverandre: q Der f C er komplementet til f, dvs at vi erstatter 1 med 0 og 0 med 1, og Ŝ er strukturelementet rotert 180 o. q For å dilatere f med symmetrisk S kan vi erodere komplementet til f med S, og ta komplementet av resultatet. q Både dilasjon og erosjon kan utføres av samme prosedyre, hvis vi kan rotere et strukturelement og finne komplementet til et bilde. komplementet 00000000000 0011100 00011100100 000100 0000100 00000100100 00000010100 00000000000 dilatert med 11111111111 1100011 11100011011 111011 1111011 11111011011 11111101011 11111111111 erodert med 010 111 010 gir 000000 0011100 0111110 00111101110 00001111110 00000010100 000000 111111 1100011 1000001 11000010001 11110000001 11111101011 111111 og disse bildene er komplementære 18. 05. 2011 19 / 38

Dualitet – II q Betrakt et binært bilde som en samling av sammenhengende regioner av piksler med verdi 1 på en bakgrunn av piksler med verdi 0. q Erosjon er å finne de posisjonene der strukturelementet passer inni regionene. q Dilasjon er å finne de posisjonene der (det transponerte) strukturelementet passer inni bakgrunnen, og så komplementere resultatet. q Dermed er det lett å se at erosjon med et sirkelformet element runder av konkave objekt-hjørner, mens dilasjon med samme element runder av konvekse objekt-hjørner. 18. 05. 2011 20 / 38

Dilasjon: Andre egenskaper § Dilasjon er kommutativ. Det er en konvensjon i faget å la første operand være bildet og andre være strukturelementet (som er mindre), men § Dilasjon er assosiativ. § Dette er veldig nyttig hvis vi ser at strukturelementet S kan dekomponeres, dvs at S er S 1 dilatert med S 2. Da kan vi spare en del regnetid. Eksempel: 18. 05. 2011 21 / 38

Erosjon: Andre egenskaper § Erosjon er IKKE kommutativ § Erosjon av snittet av to mengder er gitt ved snittet av de to erosjonene: § Suksessiv erosjon (eller dilasjon) av bildet f med A og så med B er ekvivalent med erosjon (dilasjon) av bildet f med A dilatert med B 18. 05. 2011 22 / 38

Åpning q En erosjon av et bilde fjerner alle stukturer som ikke kan inneholde strukturelementet, og ”krymper” alle andre strukturer. q Hvis vi dilaterer resultatet av en erosjon med samme strukturelement, vil de strukturer som ”overlevde” erosjonen bli gjenskapt. q Dette er en morfologisk åpning. q Navnet skyldes at operasjonen kan skape en åpning mellom to strukturer som bare henger sammen i en tynn bro, uten å krympe de to strukturene, slik som en erosjon alene ville gjort. 18. 05. 2011 23 / 38

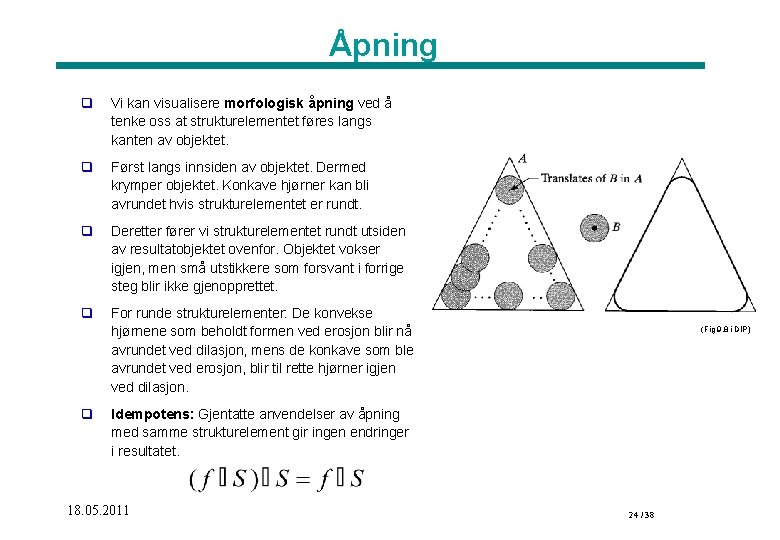
Åpning q Vi kan visualisere morfologisk åpning ved å tenke oss at strukturelementet føres langs kanten av objektet. q Først langs innsiden av objektet. Dermed krymper objektet. Konkave hjørner kan bli avrundet hvis strukturelementet er rundt. q Deretter fører vi strukturelementet rundt utsiden av resultatobjektet ovenfor. Objektet vokser igjen, men små utstikkere som forsvant i forrige steg blir ikke gjenopprettet. q For runde strukturelementer: De konvekse hjørnene som beholdt formen ved erosjon blir nå avrundet ved dilasjon, mens de konkave som ble avrundet ved erosjon, blir til rette hjørner igjen ved dilasjon. q (Fig 9. 8 i DIP) Idempotens: Gjentatte anvendelser av åpning med samme strukturelement gir ingen endringer i resultatet. 18. 05. 2011 24 / 38

Lukking q En dilasjon av et bilde utvider objektet, fyller i hull og innbuktninger i omrisset. q Hvis vi eroderer resultatet av en dilasjon med det roterte strukturelementet, vil objektene stort sett beholde sin størrelse og form, men innbuktninger som er fylt igjen ved dilasjonen vil ikke gjenoppstå. Objekter som er smeltet sammen ved dilasjonen vil ikke bli adskilt igjen. q Dette er en morfologisk lukking. q Navnet skyldes at operasjonen kan lukke en åpning mellom to strukturer som bare er adskilt med et lite gap, uten at de to regionene vokser, slik som en dilasjon ville ha gjort. 18. 05. 2011 25 / 38

Lukking II q Vi kan visualisere morfologisk lukking ved å tenke oss at strukturelementet føres langs kanten av objektet. q Først langs utsiden av objektet. Dermed vokser objektet. Konvekse hjørner kan bli avrundet. q Deretter fører vi strukturelementet rundt innsiden av resultatobjektet ovenfor. Objektet krymper igjen, men små ”viker” som forsvant i forrige steg blir ikke gjenopprettet. (Fig 9. 9 i DIP) q Idempotens: Gjentatte anvendelser av lukking med samme strukturelement gir ingen endringer i resultatet. 18. 05. 2011 26 / 38

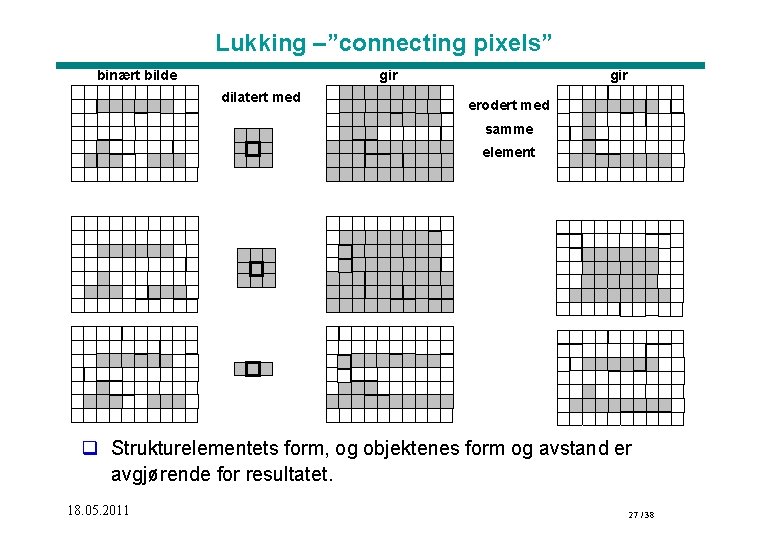
Lukking –”connecting pixels” binært bilde gir dilatert med gir erodert med samme element q Strukturelementets form, og objektenes form og avstand er avgjørende for resultatet. 18. 05. 2011 27 / 38

Dualitet mellom åpning og lukking q Lukking er en dual operasjon til åpning, og omvendt. q Lukking av et binært bilde med et strukturelement kan gjøres ved å ta komplementet til bildet, åpne det med strukturelementet, og ta komplementet av resultatet. q Og omvendt: Åpning av et binært bilde med strukturelementet kan gjøres ved å ta komplementet til bildet, lukke det med strukturelementet, og ta komplementet av resultatet. q Vi kan altså utføre begge operasjonene med kode bare for den ene, hvis vi har kode for å produsere komplementet til et binært bilde. q Lukking er en ekstensiv transformasjon (piksler legges til). q Åpning er en antiekstensiv transformasjon (piksler fjernes). 18. 05. 2011 28 / 38

Eksempel - Åpning som støyfjerner Åpning med 7 x 7 sirkulært strukturelement 18. 05. 2011 (Bilder hentet fra http: //homepages. inf. ed. ac. uk/rbf/HIPR 2/) 29 / 38

Eksempel – Formseparering ved åpning Åpning med sirkulært strukturelement 18. 05. 2011 30 / 38

Eksempel – Filtrering ved lukking Lukking med 3 x 3 strukturelement 18. 05. 2011 31 / 38

Eksempel – Filtrering ved åpning og lukking 18. 05. 2011 32 / 38

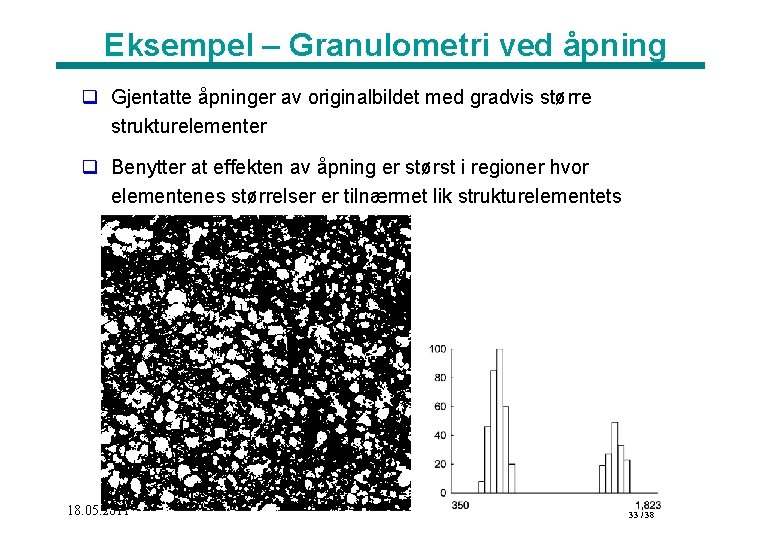
Eksempel – Granulometri ved åpning q Gjentatte åpninger av originalbildet med gradvis større strukturelementer q Benytter at effekten av åpning er størst i regioner hvor elementenes størrelser er tilnærmet lik strukturelementets 18. 05. 2011 33 / 38

Åpning ved rekonstruksjon q Erosjonen som vanlig, men hvor dilasjonen ”begrenses” av originalbildet og gjentas til ingen endring q Hente ut objekter som inneholder strukturelementet 18. 05. 2011 34 / 38

“Hit or miss”-transformasjonen q Dette er en transformasjon som brukes til å finne et bestemt mønster i et bilde. q Strukturelementet er et par [s 1, s 2] som er disjunkte mengder. q Et objektpiksel bevares kun hvis s 1 passer innenfor og s 2 passer utenfor objektet. q Eksempel på bruk: § Finne bestemte strukturer. § Fjerne enkeltpiksler. § Benyttet i ”tynning” 18. 05. 2011 35 / 38

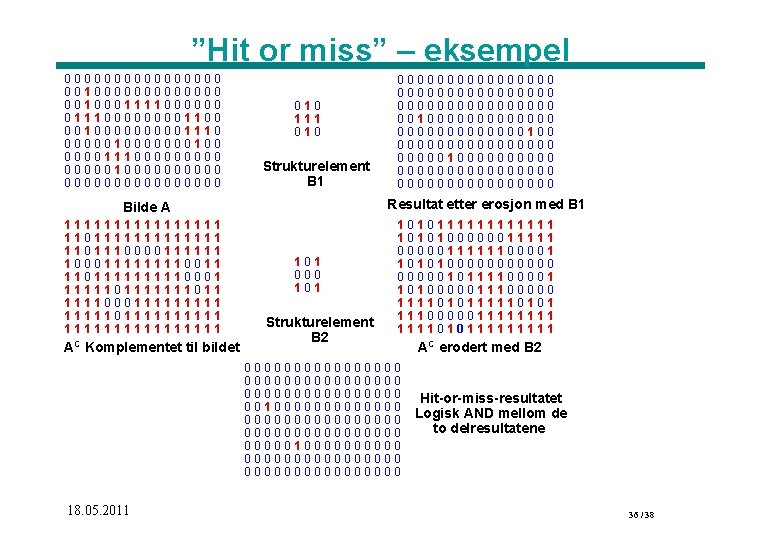
”Hit or miss” – eksempel 00000000 0010000000 0010001111000000 011100001100 001000001110 00000100 000011100000100000000 010 111 010 Strukturelement B 1 Resultat etter erosjon med B 1 Bilde A 11111111 1101111111 1101110000111111 100011110011 110111110001 11111011 111100011111011111111 AC Komplementet til bildet 0000000000000000 0010000000100 00000000100000000000 101 000 101 Strukturelement B 2 1010111111 1010100000011111100001 1010100000010111100001 1010000011100000 11110101 11100000111101011111 0000000000000000 0010000000000000 00000100000000000 18. 05. 2011 AC erodert med B 2 Hit-or-miss-resultatet Logisk AND mellom de to delresultatene 36 / 38

Morfologisk tynning q Morfologisk tynning: gjentatt med en sekvens av strukturelementer, Bk q Strukturelementene sørger for å fjerne piksler som ikke er § En isolert piksel § En piksel som ville endre “konnektiviteten”/dele objekter § Forkorter linjer 18. 05. 2011 37 / 38

Oppsummering q Grunnleggende begreper § Strukturelement (med origo) § Erosjon § Dilasjon § Dualitet § Åpning (erosjon etterfulgt av dilasjon) § Lukking (dilasjon etterfulgt av erosjon) § Hit-or-miss q Eksempler på anvendelser 18. 05. 2011 38 / 38