Image Transforms and Image Enhancement in Frequency Domain




































- Slides: 58

Image Transforms and Image Enhancement in Frequency Domain Lecture 5, Feb 25 th, 2008 Lexing Xie EE 4830 Digital Image Processing http: //www. ee. columbia. edu/~xlx/ee 4830/ thanks to G&W website, Mani Thomas, Min Wu and Wade Trappe for slide materials

roadmap n n 2 D-DFT definitions and intuitions DFT properties, applications pros and cons DCT

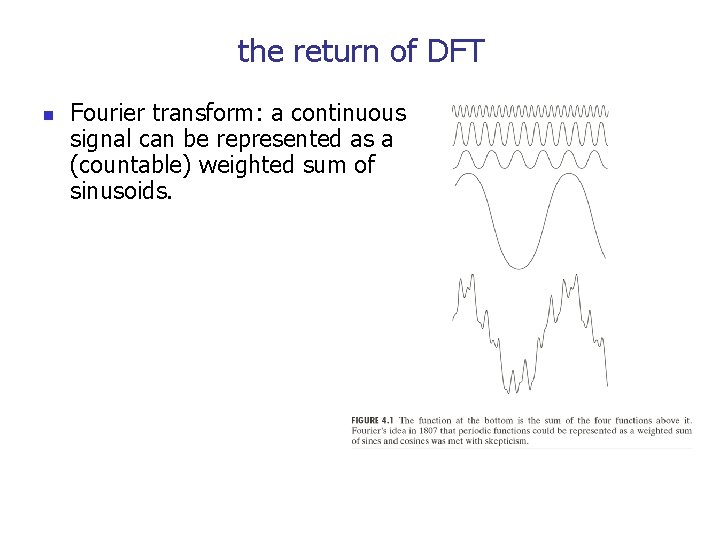
the return of DFT n Fourier transform: a continuous signal can be represented as a (countable) weighted sum of sinusoids.

warm-up brainstorm n Why do we need image transform?

why transform? n Better image processing n n Take into account long-range correlations in space Conceptual insights in spatial-frequency information. what it means to be “smooth, moderate change, fast change, …” n Fast computation: convolution vs. multiplication n Alternative representation and sensing n n Obtain transformed data as measurement in radiology images (medical and astrophysics), inverse transform to recover image Efficient storage and transmission n Energy compaction Pick a few “representatives” (basis) Just store/send the “contribution” from each basis ?

outline n n why transform 2 D Fourier transform n n n a picture book for DFT and 2 D-DFT properties implementation applications discrete cosine transform (DCT) n n definition & visualization Implementation next lecture: transform of all flavors, unitary transform, KLT, others …

1 -D continuous FT n n 1 D – FT 1 D – DFT of length N real(g( x)) imag(g( x)) =0 =7 x x

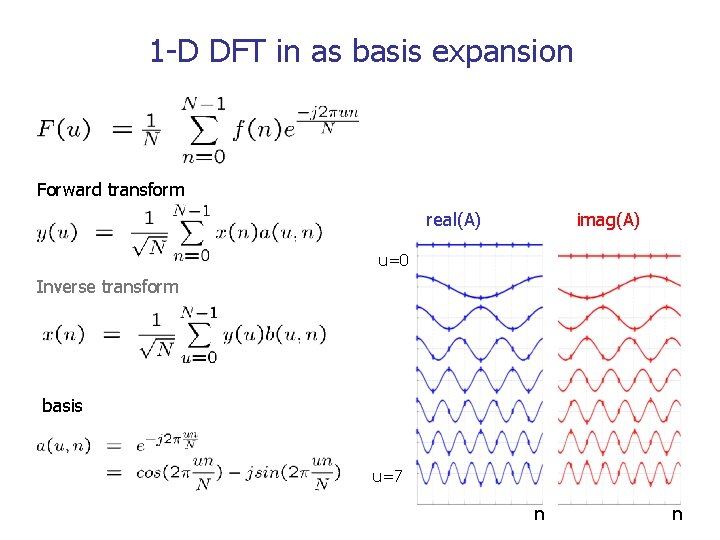
1 -D DFT in as basis expansion Forward transform real(A) imag(A) u=0 Inverse transform basis u=7 n n

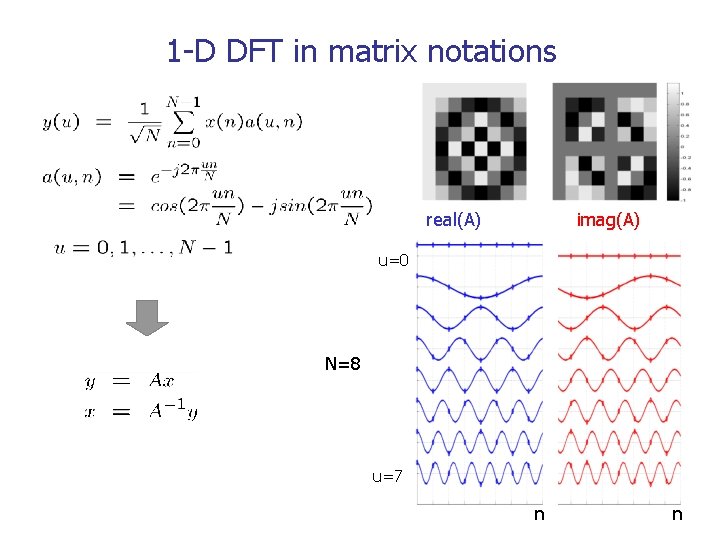
1 -D DFT in matrix notations real(A) imag(A) u=0 N=8 u=7 n n

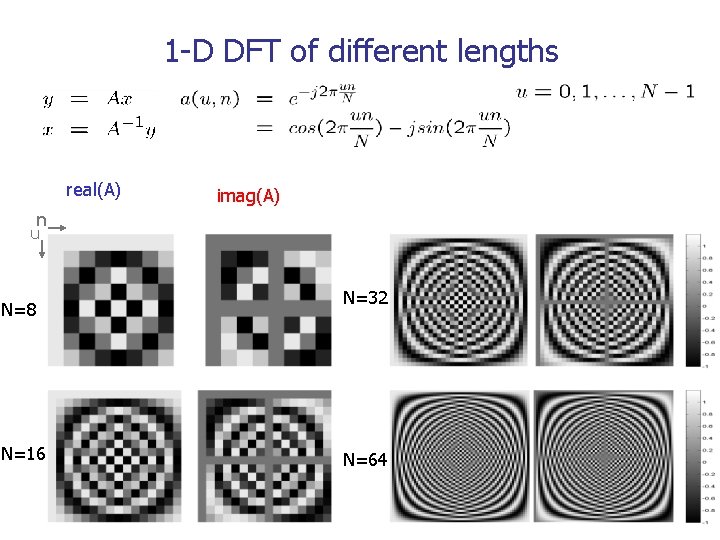
1 -D DFT of different lengths real(A) imag(A) n u N=8 N=16 N=32 N=64

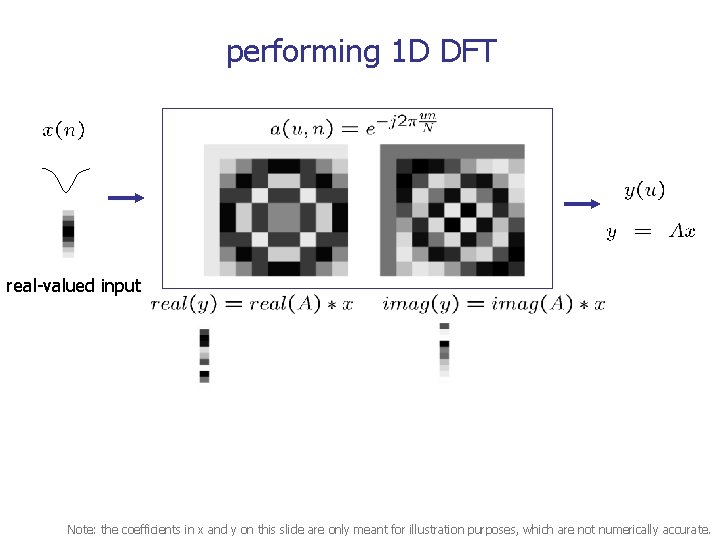
performing 1 D DFT real-valued input Note: the coefficients in x and y on this slide are only meant for illustration purposes, which are not numerically accurate.

another illustration of 1 D-DFT real-valued input Note: the coefficients in x and y are not numerically accurate

from 1 D to 2 D 1 D 2 D ?

Computing 2 D-DFT IDFT n Discrete, 2 -D Fourier & inverse Fourier transforms are implemented in fft 2 and ifft 2, respectively fftshift: Move origin (DC component) to image center for display n Example: n >> >> I = imread(‘test. png’); F = fftshift(fft 2(I)); imshow(log(abs(F)), []); imshow(angle(F), []); % % Load grayscale image Shifted transform Show log magnitude Show phase angle

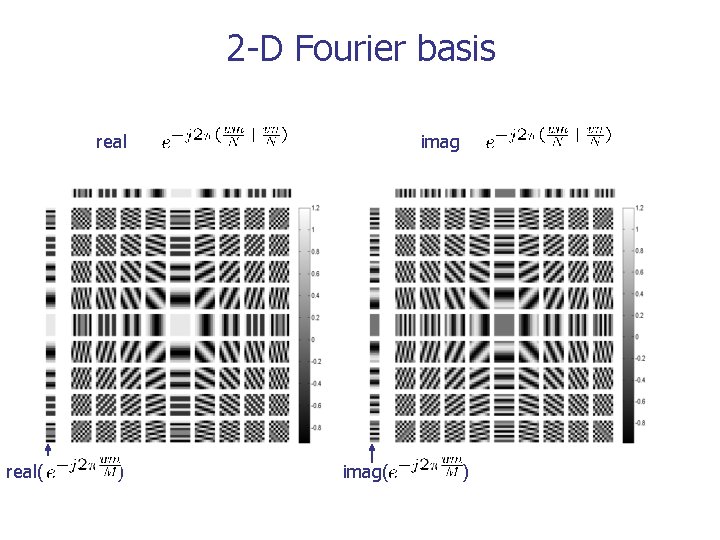
2 -D Fourier basis real( ) imag( )

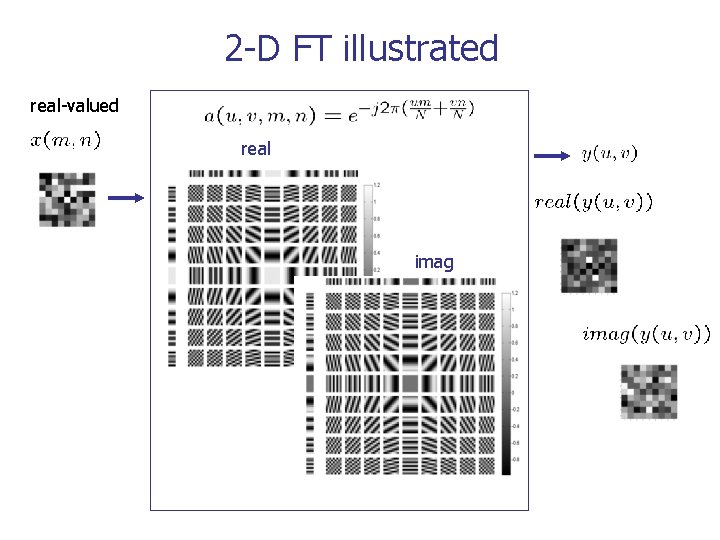
2 -D FT illustrated real-valued real imag

notes about 2 D-DFT n Output of the Fourier transform is a complex number n n Decompose the complex number as the magnitude and phase components In Matlab: u = real(z), v = imag(z), r = abs(z), and theta = angle(z)

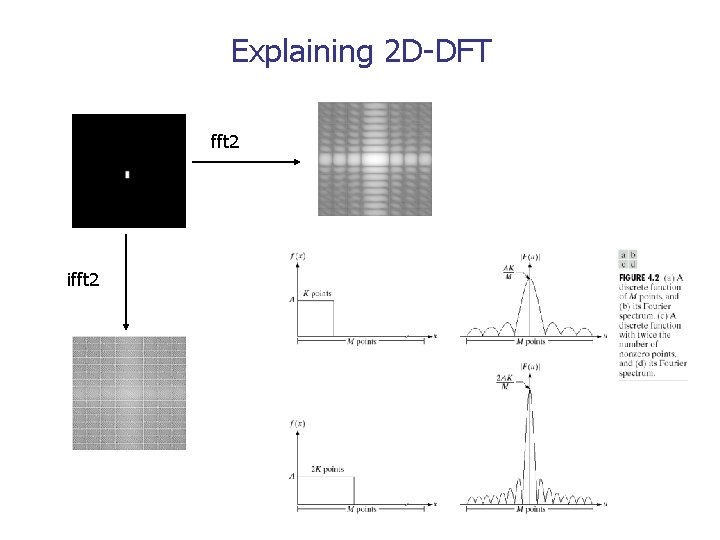
Explaining 2 D-DFT fft 2 ifft 2


circular convolution and zero padding

zero padded filter and response

zero padded filter and response

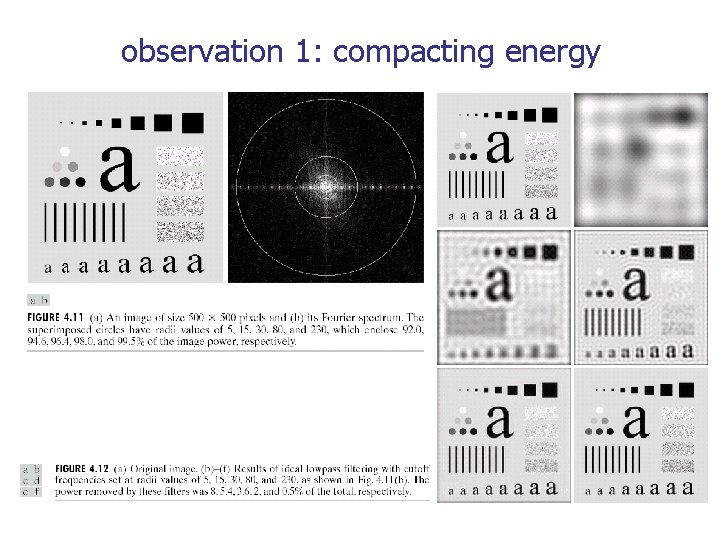
observation 1: compacting energy

observation 2: amplitude vs. phase n n Amplitude: relative prominence of sinusoids Phase: relative displacement of sinusoids

another example: amplitude vs. phase A = “Aron” P = “Phyllis” FA = fft 2(A) FP = fft 2(P) log(abs(FA)) log(abs(FP)) angle(FA) ifft 2(abs(FA), angle(FP)) Adpated from http: //robotics. eecs. berkeley. edu/~sastry/ee 20/vision 2. html angle(FP) ifft 2(abs(FP), angle(FA))

fast implementation of 2 -D DFT n 2 Dimensional DFT is separable 1 -D DFT of f(m, n) w. r. t n 1 -D DFT of F(m, v) w. r. t m n n n 1 D FFT: O(N¢log 2 N) 2 D DFT naïve implementation: O(N 4) 2 D DFT as 1 D FFT for each row and then for each column

Implement IDFT as DFT 2 IDFT 2

Properties of 2 D-DFT


duality result

outline n n why transform 2 D Fourier transform n n n a picture book for DFT and 2 D-DFT properties implementation applications discrete cosine transform (DCT) n n definition & visualization implementation

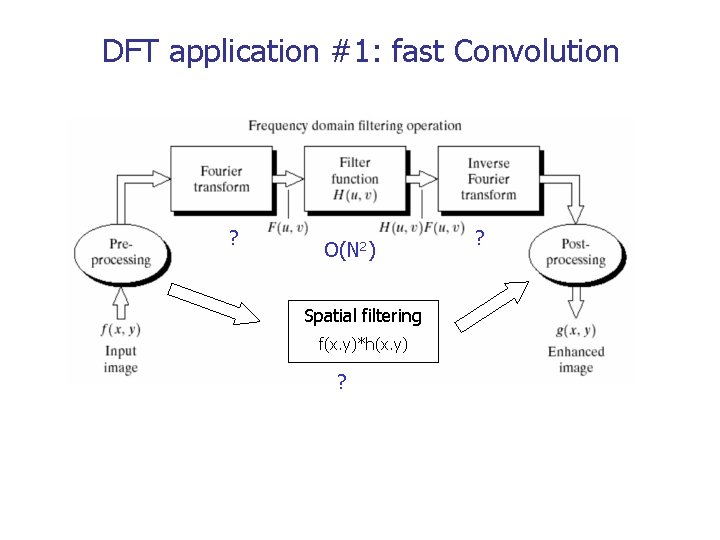
DFT application #1: fast Convolution ? O(N 2) Spatial filtering f(x. y)*h(x. y) ? ?

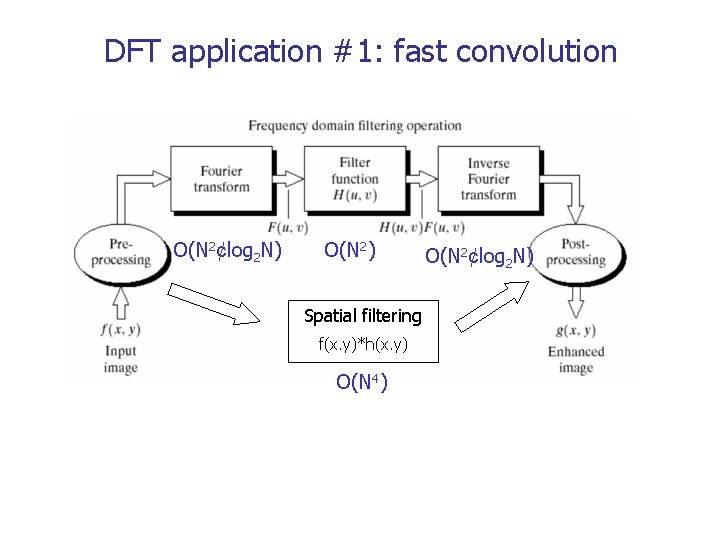
DFT application #1: fast convolution O(N 2¢log 2 N) O(N 2) Spatial filtering f(x. y)*h(x. y) O(N 4) O(N 2¢log 2 N)

DFT application #2: feature correlation n Find letter “a” in the following image bw = imread('text. png'); a = imread(‘letter_a. png'); % Convolution is equivalent to correlation if you rotate the convolution kernel by 180 deg C = real(ifft 2(bw). *fft 2(rot 90(a, 2), 256))); % Use a threshold that's a little less than max. % Display showing pixels over threshold. thresh =. 9*max(C(: )); figure, imshow(C > thresh) from Matlab image processing demos.

DFT application #3: image filters n Zoology of image filters n n Smoothing / Sharpening / Others Support in time vs. support in frequency c. f. “FIR / IIR” Definition: spatial domain/frequency domain Separable / Non-separable

smoothing filters: ideal low-pass

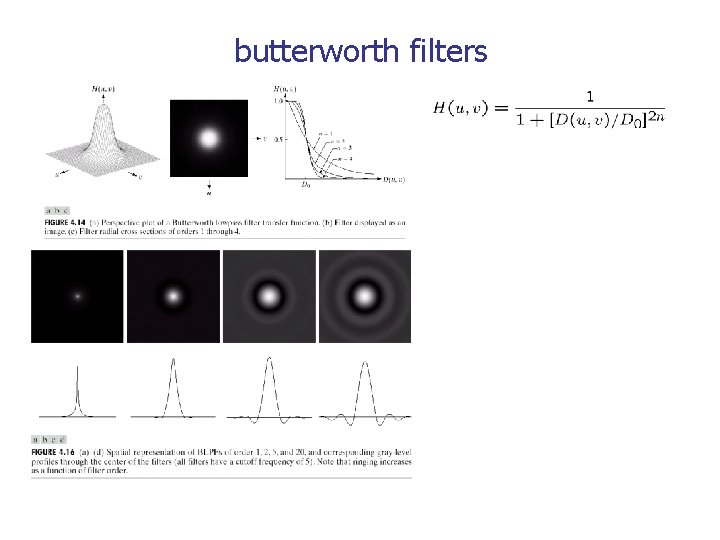
butterworth filters

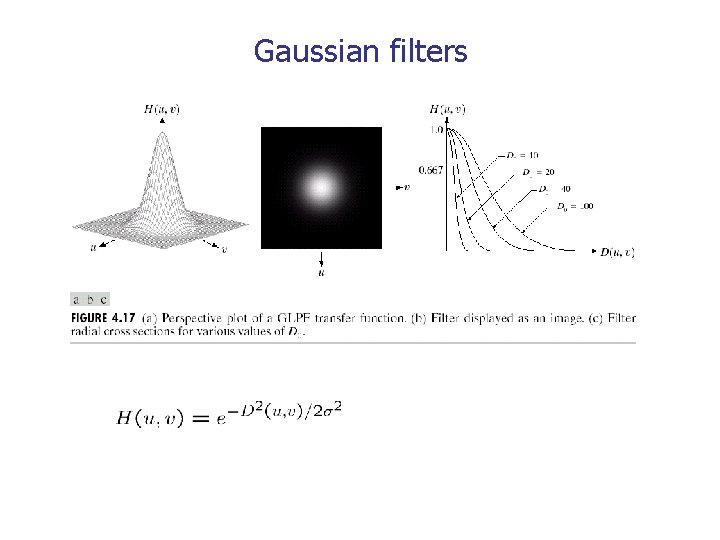
Gaussian filters

low-pass filter examples

smoothing filter application 1 text enhancement

smoothing filter application 2 beautify a photo

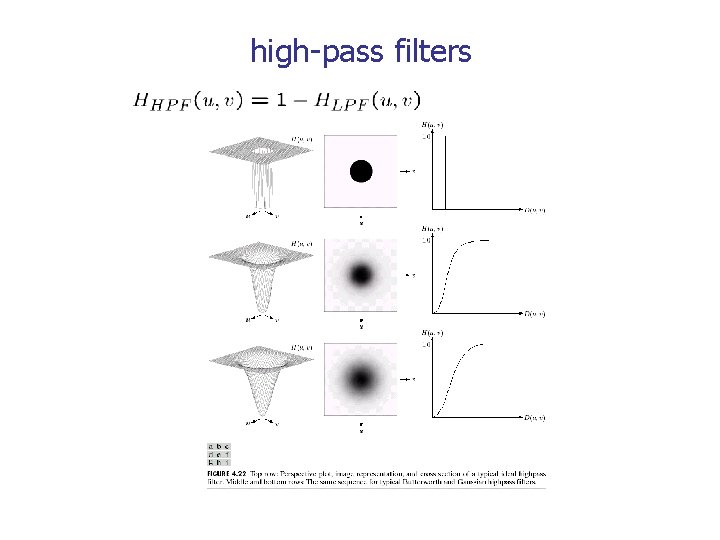
high-pass filters

sobel operator in frequency domain Question: Sobel vs. other high-pass filters? Spatial vs frequency domain implementation?

high-pass filter examples

outline n n why transform 2 D Fourier transform n n n a picture book for DFT and 2 D-DFT properties implementation applications in enhancement, correlation discrete cosine transform (DCT) n n definition & visualization implementation

Is DFT a Good (enough) Transform? n Theory n Implementation n Application

The Desirables for Image Transforms n Theory n n n Implementation n n Inverse transform available Energy conservation (Parsevell) Good for compacting energy Orthonormal, complete basis (sort of) shift- and rotation invariant Real-valued Separable Fast to compute w. butterfly-like structure Same implementation forward and inverse transform Application n n Useful for image enhancement Capture perceptually meaningful structures in images DFT X X ? X X x X X X ? ? ?

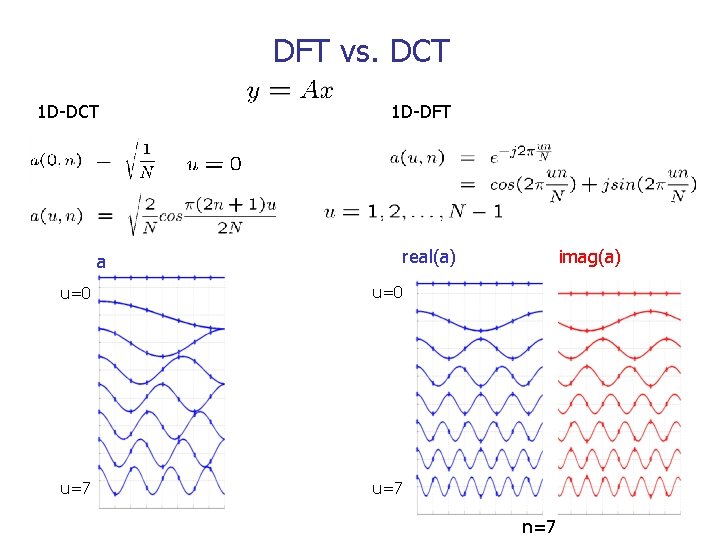
DFT vs. DCT 1 D-DFT real(a) a u=0 u=7 imag(a) n=7

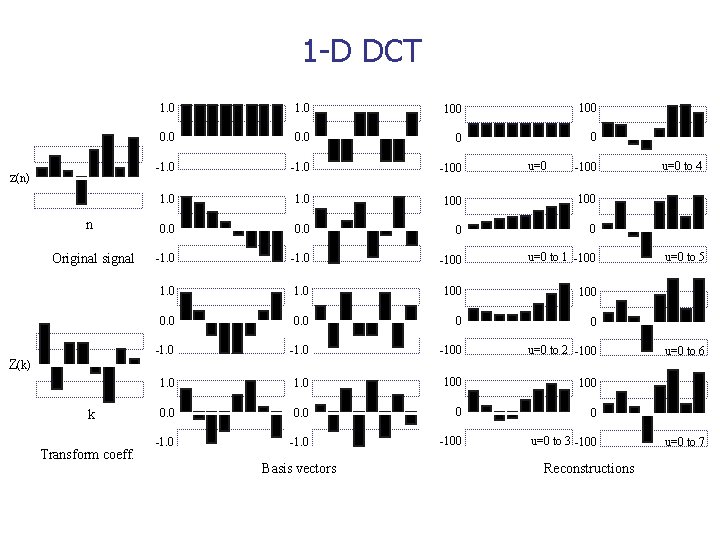
1 -D Discrete Cosine Transform (DCT) n n Transform matrix A n a(k, n) = (0) for k=0 n a(k, n) = (k) cos[ (2 n+1)/2 N] for k>0 A is real and orthogonal n rows of A form orthonormal basis n A is not symmetric! n DCT is not the real part of unitary DFT!

1 -D DCT z(n) n Original signal Z(k) k Transform coeff. 1. 0 100 100 0. 0 0 0 -100 u=0 to 1 -100 1. 0 100 0. 0 0 0 -100 u=0 to 2 -100 1. 0 100 0. 0 0 0 -100 u=0 to 3 -100 Basis vectors u=0 -100 Reconstructions u=0 to 4 u=0 to 5 u=0 to 6 u=0 to 7

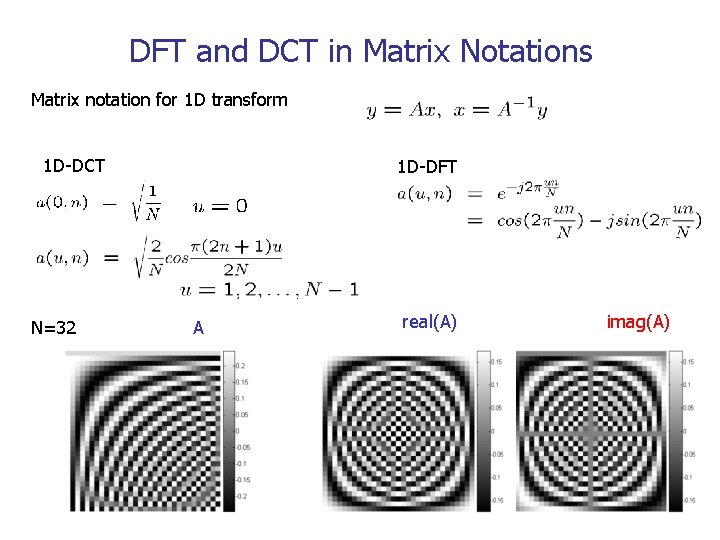
DFT and DCT in Matrix Notations Matrix notation for 1 D transform 1 D-DCT N=32 1 D-DFT A real(A) imag(A)

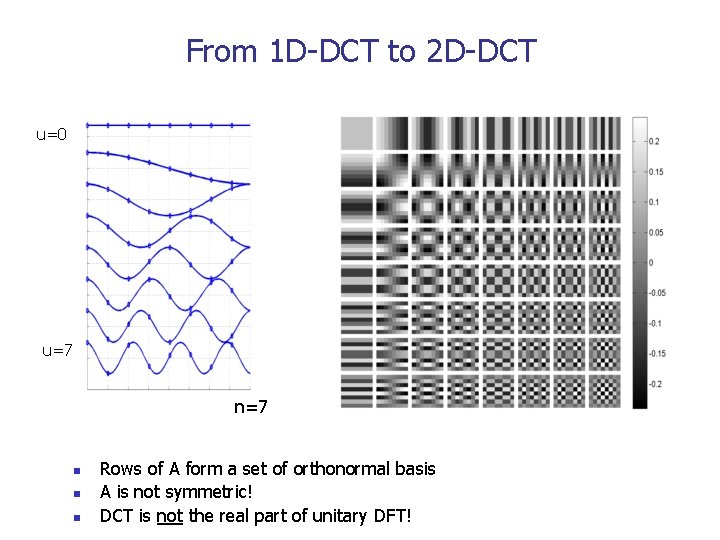
From 1 D-DCT to 2 D-DCT u=0 u=7 n n n Rows of A form a set of orthonormal basis A is not symmetric! DCT is not the real part of unitary DFT!

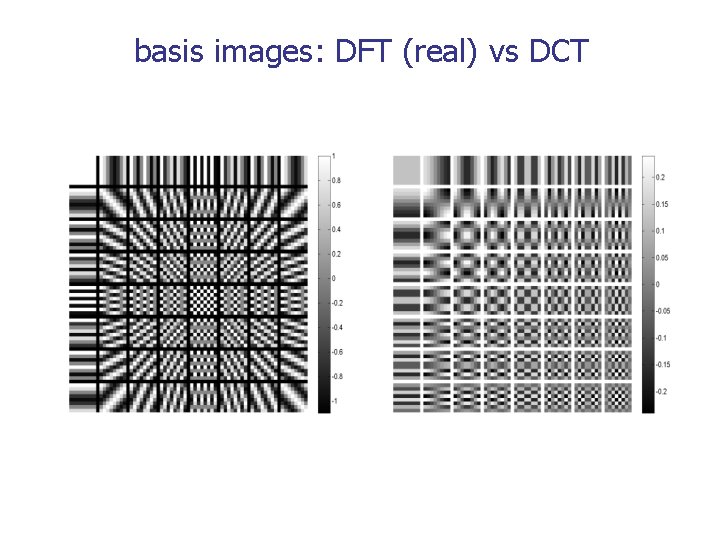
basis images: DFT (real) vs DCT

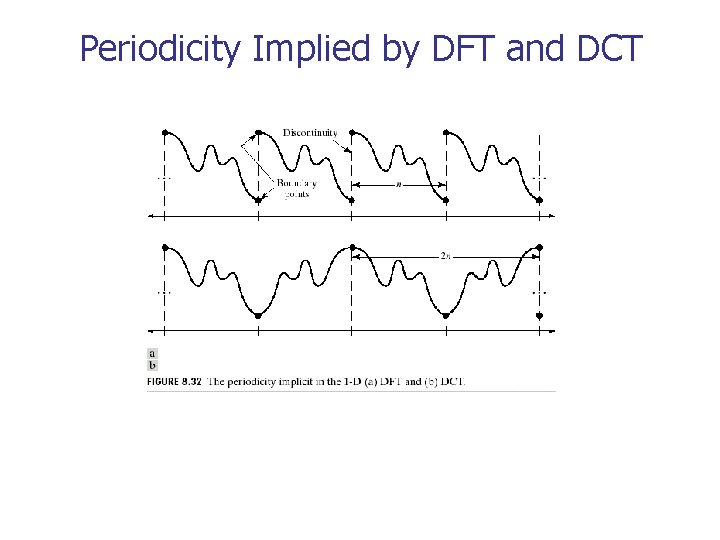
Periodicity Implied by DFT and DCT

DFT and DCT on Lena DFT 2 DCT 2 Shift low-freq to the center Assume periodic and zero-padded … Assume reflection …

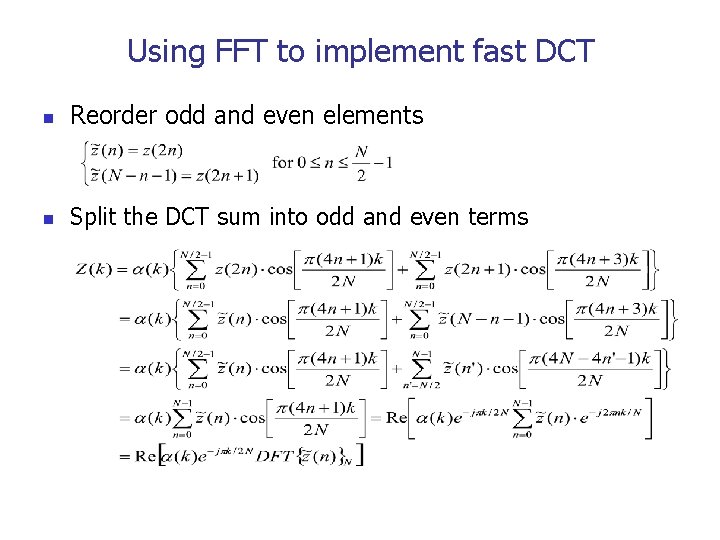
Using FFT to implement fast DCT n Reorder odd and even elements n Split the DCT sum into odd and even terms

The Desirables for Image Transforms n Theory n n n Implementation n n Inverse transform available Energy conservation (Parsevell) Good for compacting energy Orthonormal, complete basis (sort of) shift- and rotation invariant Real-valued Separable Fast to compute w. butterfly-like structure Same implementation forward and inverse transform Application n n Useful for image enhancement Capture perceptually meaningful structures in images DFT DCT X X ? ? X X x X X X X X ? ? ?

Summary of Lecture 5 n n Why we need image transform DFT revisited n Definitions, properties, observations, implementations, applications n What do we need for a transform DCT n Coming in Lecture 6: n n n Unitary transforms, KL transform, DCT examples and optimality for DCT and KLT, other transform flavors, Wavelets, Applications Readings: G&W chapter 4, chapter 5 of Jain has been posted on Courseworks “Transforms” that do not belong to lectures 5 -6: Rodon transform, Hough transform, …
 Combining spatial enhancement methods
Combining spatial enhancement methods Image enhancement in spatial domain
Image enhancement in spatial domain Image enhancement in spatial domain
Image enhancement in spatial domain Image enhancement in spatial domain
Image enhancement in spatial domain Digital image processing
Digital image processing Frequency domain to time domain
Frequency domain to time domain Z domain to frequency domain
Z domain to frequency domain Z domain to frequency domain
Z domain to frequency domain Table of z transforms
Table of z transforms What is enhancement in the spatial domain?
What is enhancement in the spatial domain? High pass filter radiology
High pass filter radiology Frequency domain image
Frequency domain image Image processing frequency domain
Image processing frequency domain Image transforms
Image transforms Image enhancement in night vision technology
Image enhancement in night vision technology Objective of image enhancement
Objective of image enhancement Contoh pelembutan citra
Contoh pelembutan citra Point processing
Point processing Inverse log transformation in image processing
Inverse log transformation in image processing Image enhancement
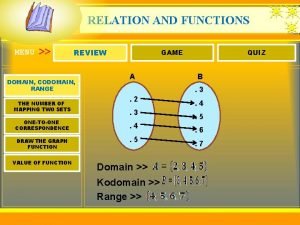
Image enhancement Domain codomain range
Domain codomain range The designer expresses the ideas in terms related to the
The designer expresses the ideas in terms related to the Kl transform example
Kl transform example Joint relative frequency
Joint relative frequency Probability with relative frequency
Probability with relative frequency Constant phase difference
Constant phase difference Vmax = aw
Vmax = aw Relative frequency bar chart
Relative frequency bar chart Joint frequency vs marginal frequency
Joint frequency vs marginal frequency Marginal frequency distribution
Marginal frequency distribution Laplace frequency domain
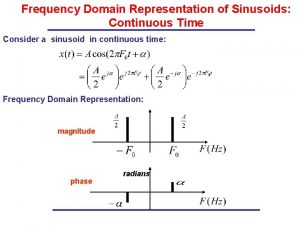
Laplace frequency domain Frequency domain
Frequency domain Differentiation property of fourier transform proof
Differentiation property of fourier transform proof Define circular convolution
Define circular convolution Erp boot camp
Erp boot camp Laser synchronization
Laser synchronization Domain specific vs domain general
Domain specific vs domain general Domain specific vs domain general
Domain specific vs domain general Problem domain vs knowledge domain
Problem domain vs knowledge domain S domain to z domain
S domain to z domain Eurylochus odyssey
Eurylochus odyssey Laplace tranform table
Laplace tranform table The unit that transforms data into information is the:
The unit that transforms data into information is the: Discontinuous forcing functions
Discontinuous forcing functions This transforms a bare stage into the world of the play
This transforms a bare stage into the world of the play What is the drama
What is the drama Nassim ammour
Nassim ammour Transforms eroded parts of earth's surface into lakes
Transforms eroded parts of earth's surface into lakes Friction transforms mechanical energy to
Friction transforms mechanical energy to Which phase transforms srs document
Which phase transforms srs document Piere simon laplace
Piere simon laplace Friction transforms mechanical energy to
Friction transforms mechanical energy to Photosynthesis transforms light energy into chemical energy
Photosynthesis transforms light energy into chemical energy Centre for learning enhancement and research
Centre for learning enhancement and research Listening and communication enhancement
Listening and communication enhancement Environmental enhancement and mitigation program
Environmental enhancement and mitigation program Complex sentence examples
Complex sentence examples Www.dfps.state.tx.us/training/trauma informed care/
Www.dfps.state.tx.us/training/trauma informed care/ Digital print enhancement
Digital print enhancement