Frequency Domain Examples Sin wave image spatial domain

  • Slides: 18
Download presentation
Frequency Domain Examples

Frequency Domain Examples

Sin wave image – spatial domain Sin wave image – frequency domain Peppers image

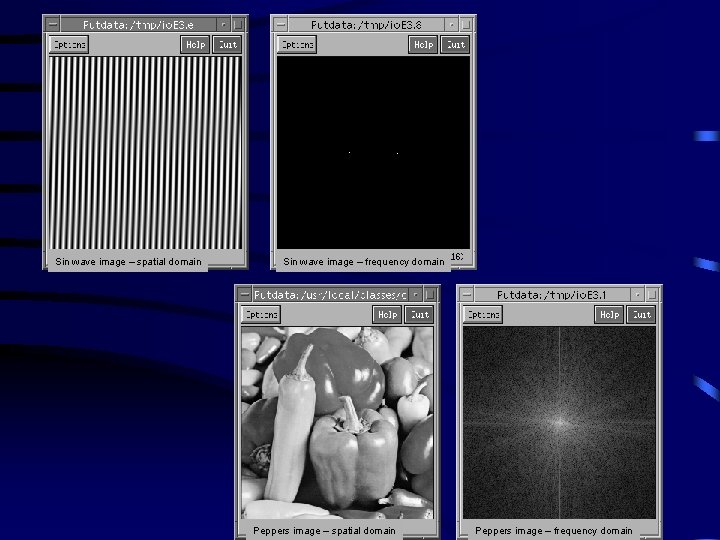
Sin wave image – spatial domain Sin wave image – frequency domain Peppers image – spatial domain Peppers image – frequency domain

Sin wave image – spatial domain Sin wave image – frequency domain Peppers image

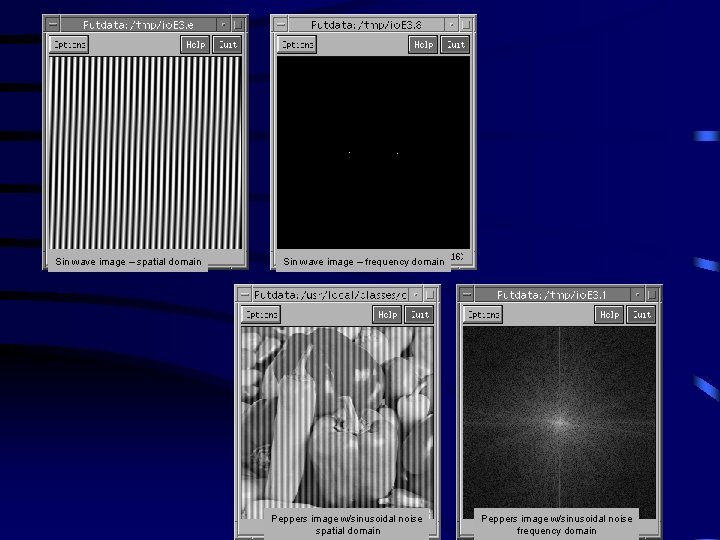
Sin wave image – spatial domain Sin wave image – frequency domain Peppers image w/sinusoidal noise spatial domain Peppers image w/sinusoidal noise frequency domain

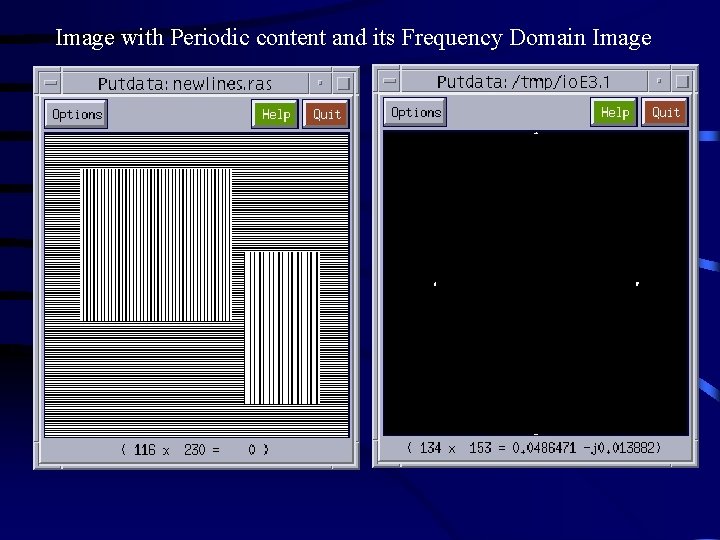
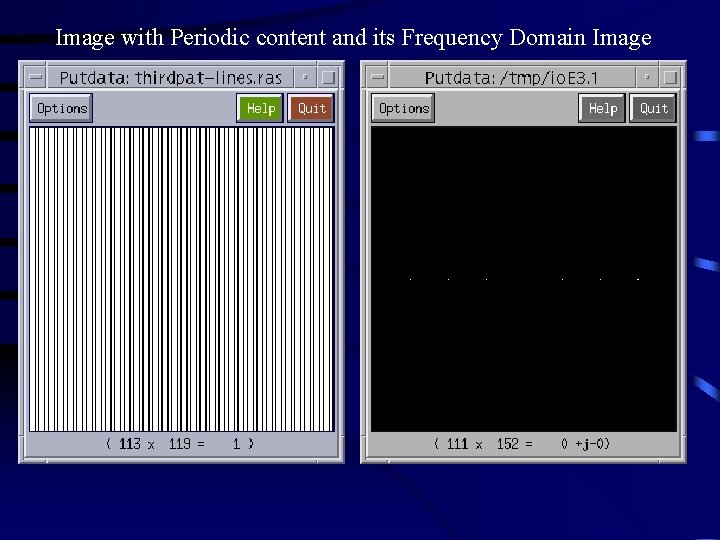
Image with Periodic content and its Frequency Domain Image

Image with Periodic content and its Frequency Domain Image

Image with Periodic content and its Frequency Domain Image

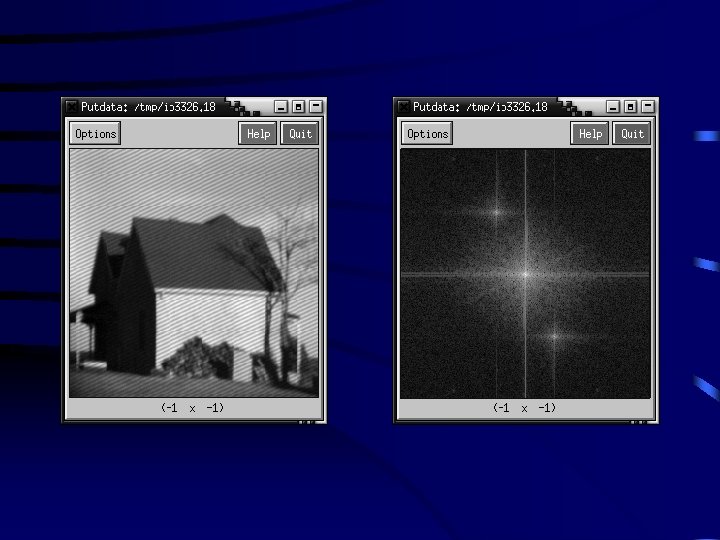
Image with Periodic content and its Frequency Domain Image

Plots of pixel values of a row from Image with Periodic content

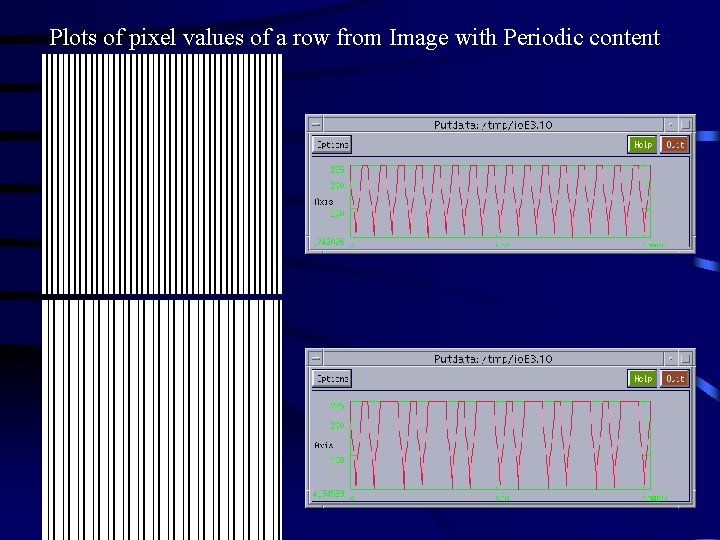
Plots of pixel values of a row from Image with Periodic content

Frequency Domain Filtering

Frequency Domain Filtering

Filtering in the spatial domain is described by the following equation: g(x, y) =

Filtering in the spatial domain is described by the following equation: g(x, y) = h(x, y)*f(x, y) where f(x, y) is the original image, h(x, y) is the filter and * denotes the convolution operation

Frequency Domain Filters Filtering in the frequency domain is described by the following equation:

Frequency Domain Filters Filtering in the frequency domain is described by the following equation: G(u, v) = H(u, v)F(u, v) is the Fourier transform of an image H(u, v) is the frequency domain filter G(u, v) is the Fourier transform of the filtered image

Ideal Filters A 2 -D ideal low-pass filter is one whose transfer function satisfies

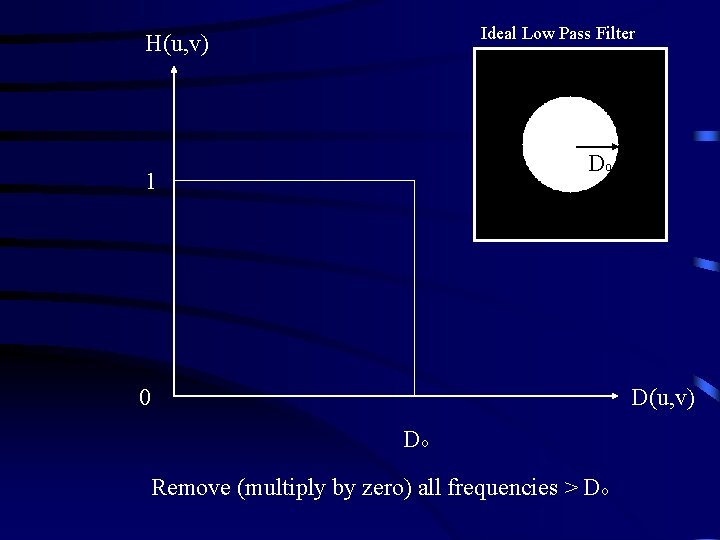
Ideal Filters A 2 -D ideal low-pass filter is one whose transfer function satisfies the relation: 1 if D(u, v) <= D o 0 if D(u, v) > D o H(u, v) = where Do is a non-negative quantity and D(u, v) is the distance from the point (u, v) to the origin of the frequency plane

Ideal Low Pass Filter H(u, v) Do 1 0 D(u, v) Do Remove (multiply

Ideal Low Pass Filter H(u, v) Do 1 0 D(u, v) Do Remove (multiply by zero) all frequencies > Do

Filtering in the Spatial domain: g(x, y) = h(x, y)*f(x, y) Filtering in the

Filtering in the Spatial domain: g(x, y) = h(x, y)*f(x, y) Filtering in the frequency domain: G(u, v) = H(u, v)F(u, v) - Fourier transform of an image H(u, v) - frequency domain filter G(u, v) - Fourier transform of the filtered image

Ideal low pass filter Forward FFT Spatial domain image Inverse FFT Frequency domain image

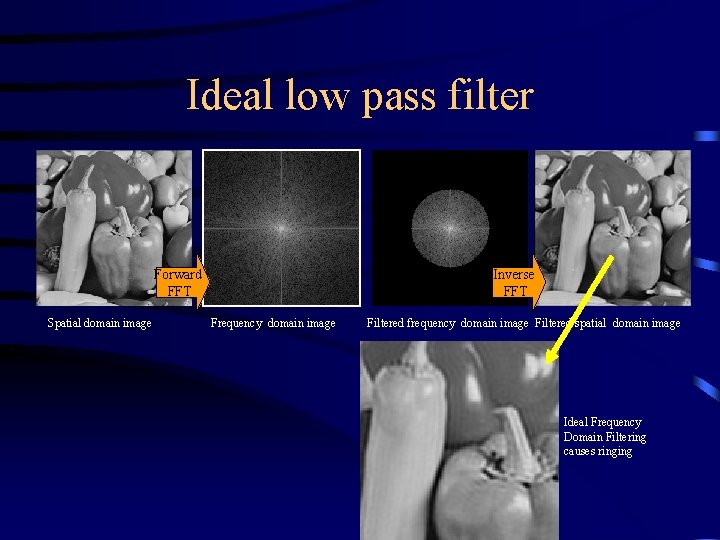
Ideal low pass filter Forward FFT Spatial domain image Inverse FFT Frequency domain image Filtered frequency domain image Filtered spatial domain image Ideal Frequency Domain Filtering causes ringing

Ideal high pass filter Forward FFT Spatial domain image Inverse FFT Frequency domain image

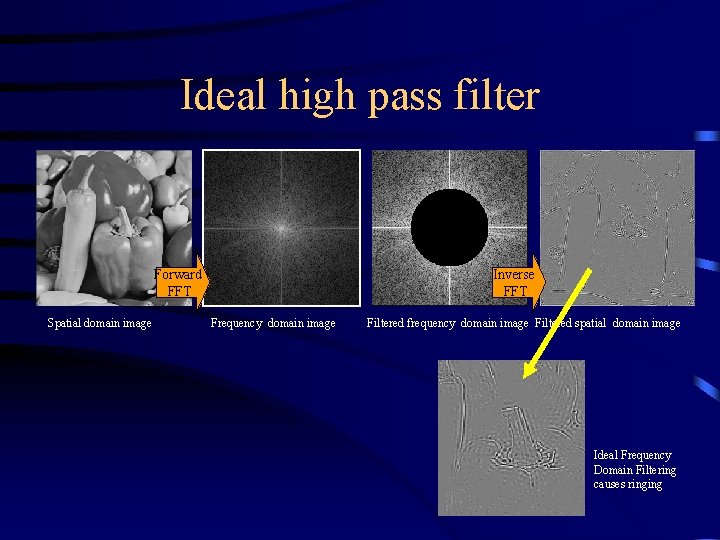
Ideal high pass filter Forward FFT Spatial domain image Inverse FFT Frequency domain image Filtered frequency domain image Filtered spatial domain image Ideal Frequency Domain Filtering causes ringing

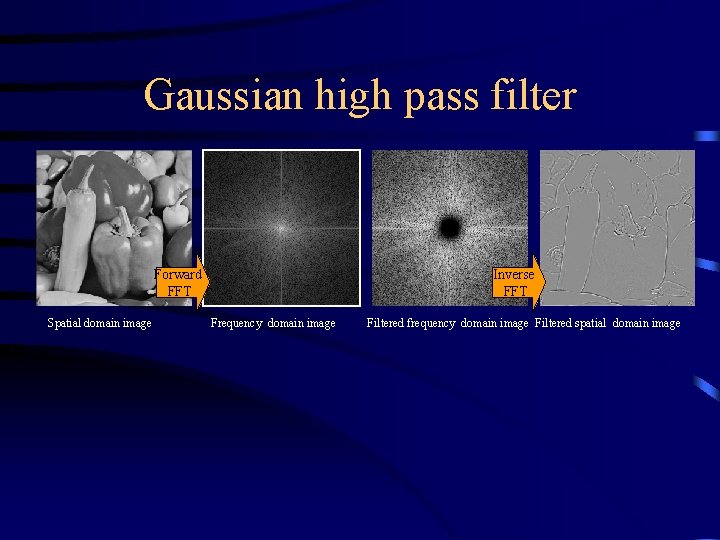
Gaussian high pass filter Forward FFT Spatial domain image Inverse FFT Frequency domain image

Gaussian high pass filter Forward FFT Spatial domain image Inverse FFT Frequency domain image Filtered frequency domain image Filtered spatial domain image

Gaussian high pass filter Forward FFT Spatial domain image Frequency domain image Filtered frequency

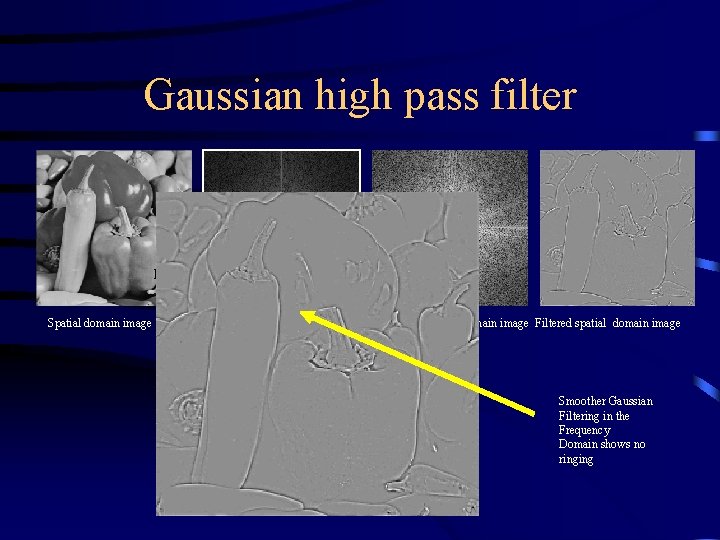
Gaussian high pass filter Forward FFT Spatial domain image Frequency domain image Filtered frequency domain image Filtered spatial domain image Smoother Gaussian Filtering in the Frequency Domain shows no ringing

Boxcar average filter – spatial domain If we imagine our ideal (unweighted boxcar average)

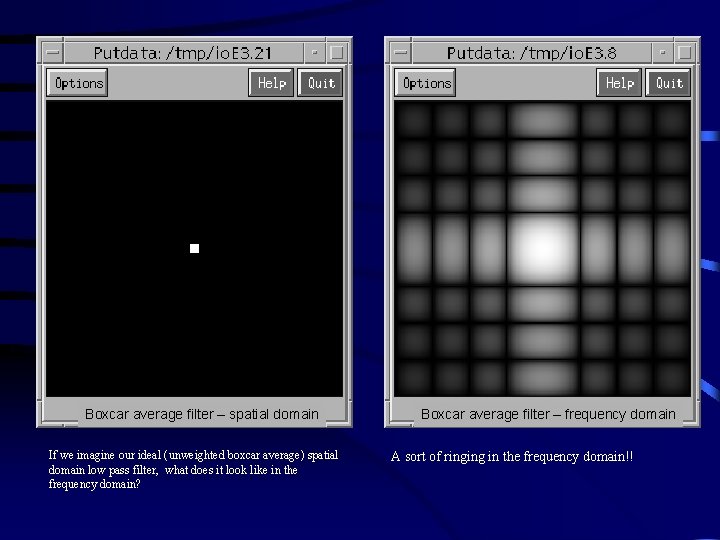
Boxcar average filter – spatial domain If we imagine our ideal (unweighted boxcar average) spatial domain low pass filter, what does it look like in the frequency domain? Boxcar average filter – frequency domain A sort of ringing in the frequency domain!!