Probability Relative and Expected Frequency Starter A man

Probability Relative and Expected Frequency

Starter • A man has a choice of five ties – 2 red, 1 black and 2 spotty. He also has a choice of five jumpers – 3 black, 1 red and 1 grey. The sample space diagram below shows the possible combinations he can have. Red (r) Black (b) Spotty (s) Black (B) Br Br Bb Bs Bs Red (R) Rr Rr Rb Rs Rs Grey (G) Gr Gr Gb Gs Gs Calculate the probability of the man wearing: a) A red jumper b) A spotty tie c) Something black d) Nothing red e) Matching jumper and tie

Relative Frequency Learning Objectives: • Know the meaning of relative frequency • Able to calculate relative frequency • Able to use relative frequency to calculate expected frequency 05/03/2021

Probability •

Complementary probability • Most events can be considered so there are only 2 outcomes: 1. an event may happen = success 2. Or may not happen = failure Pr(event happening) + Pr(event not happening) = 1 So to calculate Probability of an event not happening: Pr(event not happening) = 1 – Pr(event happening)

Relative Frequency •

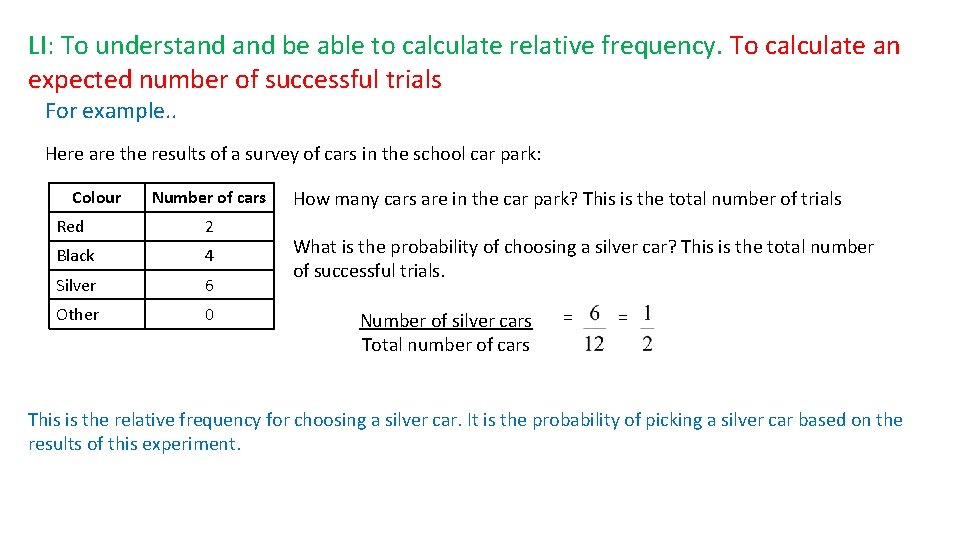
LI: To understand be able to calculate relative frequency. To calculate an expected number of successful trials For example. . Here are the results of a survey of cars in the school car park: Colour Number of cars Red 2 Black 4 Silver 6 Other 0 How many cars are in the car park? This is the total number of trials What is the probability of choosing a silver car? This is the total number of successful trials. Number of silver cars Total number of cars = = This is the relative frequency for choosing a silver car. It is the probability of picking a silver car based on the results of this experiment.

Here are the results of a survey of cars in the school car park: Colour Number of cars Red 2 Black 4 Silver 6 Other 0 Let’s calculate the relative frequencies for choosing a red car, a black car, and another coloured car. The total number of cars in the car park is 12 Red Car: Black Car: Other Cars:

Worked Example

Relative Frequency vs Expected Frequency • If I roll an unbiased die, what would I expect the relative frequency to be for each number? Number 1 2 3 4 5 6 Relative Frequency 0. 17 • As this is only theory, in reality this will almost certainly be slightly different. We will conduct an experiment to test these relative frequencies

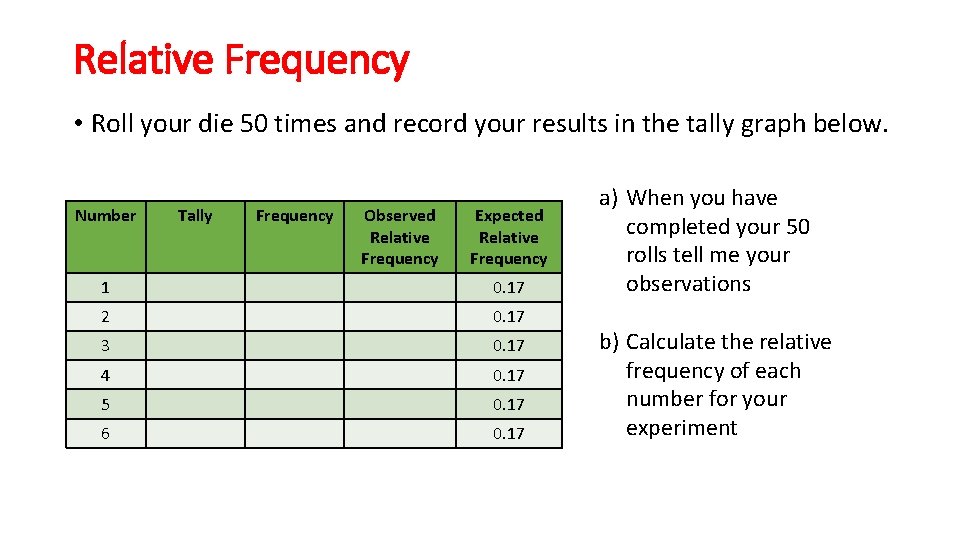
Relative Frequency • Roll your die 50 times and record your results in the tally graph below. Number Tally Frequency Observed Relative Frequency Expected Relative Frequency 1 0. 17 2 0. 17 3 0. 17 4 0. 17 5 0. 17 6 0. 17 a) When you have completed your 50 rolls tell me your observations b) Calculate the relative frequency of each number for your experiment

Swap your books with the group next to you, and see how closely your relative frequencies compare. Discuss the similarities or differences.

LI: To understand be able to calculate relative frequency. To calculate an expected frequency What if you rolled the dice 100 times? Based on the results of your experiment, and without rolling your dice 100 times, how could we calculate how many times we would expect to roll a given number on the dice? We would multiply the relative frequency by 100! = 30 Based on our data, we would expect to roll a 6, 30 times in 100 rolls.

What do you think is the formula for finding the expected number of successful trials?

LO: To understand be able to calculate relative frequency (L 6) CO: To calculate an expected number of successful trials (L 6) From your experiment, calculate how many times you would expect to roll each number on the dice after: a)100 rolls b)1000 rolls c)270 rolls d)630 rolls

Did you meet today’s Learning Objectives? LO: To understand be able to calculate relative frequency To calculate an expected number of successful trials

Write a comment about today’s lesson in green pen in your book. Complete your exit ticket – rate your behaviour 1 -5 (1 being the best, 5 being the worst) and how well you think you learnt today’s material