Il calcolo combinatorio QUANTI RAGGRUPPAMENTI Il calcolo combinatorio

Il calcolo combinatorio QUANTI RAGGRUPPAMENTI?

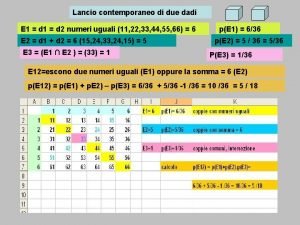
Il calcolo combinatorio Calcolo di probabilità con la teoria classica Quanto vale la probabilità che in 8 lanci di una moneta esca sempre la faccia TESTA? Quanto vale la probabilità che in 8 lanci di una moneta esca 3 sole volte la faccia TESTA? Se il prof interroga 4 alunni a caso quanto vale la probabilità che nel gruppo ci sia una femmina? Come calcolare casi favorevoli e casi possibili? Serve il calcolo combinatorio!

n Quesito 1 In quanti modi 5 amici possono occupare 3 poltrone libere in un cinema? 2 Quanti sono i numeri di 4 cifre DISTINTE che si possono formare utilizzando i numeri 1, 2, 3, 4, 5, 6, 7? 3 Quanti sono i numeri di 4 cifre ANCHE RIPETUTE che si possono formare utilizzando i numeri 1, 2, 3, 4, 5, 6, 7? 4 Quante colonne si possono giocare al TOTOCALCIO? 5 In quanti modi si può estrarre una cinquina in una ruota del gioco del Lotto? 6 In quanti modi si possono mescolare 5 liquori presi 3 alla volta per ottenere un cocktail? 7 Quanti sono gli anagrammi della parola CASO? 8 Quanti sono gli anagrammi della parola MATEMATICA? 9 In quanti modi si possono distribuire 10 caramelle uguali a 3 bambini?

Ampiezze raggruppamenti n: ampiezza del gruppo iniziale k: ampiezza del raggruppamento Quanto valgono n e k?

n Quesito n k 1 In quanti modi 5 amici possono occupare 3 poltrone libere in un cinema? 5 3 2 Quanti sono i numeri di 4 cifre DISTINTE che si possono formare utilizzando i numeri 1, 2, 3, 4, 5, 6, 7? 7 4 3 Quanti sono i numeri di 4 cifre ANCHE RIPETUTE che si possono formare utilizzando i numeri 1, 2, 3, 4, 5, 6, 7? 7 4 4 Quante colonne si possono giocare al TOTOCALCIO? 3 13 5 In quanti modi si può estrarre una cinquina in una ruota del gioco del Lotto? 90 5 6 In quanti modi si possono mescolare 5 liquori presi 3 alla volta per ottenere un cocktail? 5 3 7 Quanti sono gli anagrammi della parola CASO? 4 4 8 Quanti sono gli anagrammi della parola MATEMATICA? 10 10 9 In quanti modi si possono distribuire 10 caramelle uguali a 3 bambini? 3 10

Caratteristiche dei raggruppamenti ORDINE In alcuni raggruppamenti l’ordine con il quale prendere gli elementi è importante, ovvero due raggruppamenti che differiscono solo per l’ordine sono diversi, in altri l’ordine non è importante. RIPETIZION E In alcuni raggruppamenti gli elementi si possono ripetere in altri no.

n Quesito n k Importanza ordine Possibilità ripetizione 1 In quanti modi 5 amici possono occupare 3 poltrone libere in un cinema? 5 3 Sì No 2 Quanti sono i numeri di 4 cifre DISTINTE che si possono formare utilizzando i numeri 1, 2, 3, 4, 5, 6, 7? 7 4 Sì No 3 Quanti sono i numeri di 4 cifre ANCHE RIPETUTE che si possono 7 formare utilizzando i numeri 1, 2, 3, 4, 5, 6, 7? 4 Sì Sì 3 13 Sì Sì 90 5 No No 3 No No 4 Quante colonne si possono giocare al TOTOCALCIO? 5 In quanti modi si può estrarre una cinquina in una ruota del gioco del Lotto? 6 In quanti modi si possono mescolare 5 liquori presi 3 alla volta per 5 ottenere un cocktail? 7 Quanti sono gli anagrammi della parola CASO? 4 4 Sì No 8 Quanti sono gli anagrammi della parola MATEMATICA? 10 10 Sì No 3 10 No Sì 9 In quanti modi si possono distribuire 10 caramelle uguali a 3 bambini?

Raggruppamenti del Calcolo Combinatorio Ordine importante Ordine non importante Disposizioni Permutazioni Combinazioni Semplici Dn, k Con ripetizione D'n, k Con elementi ripetuti Pn Cn, k C'n, k Pna, b, . .

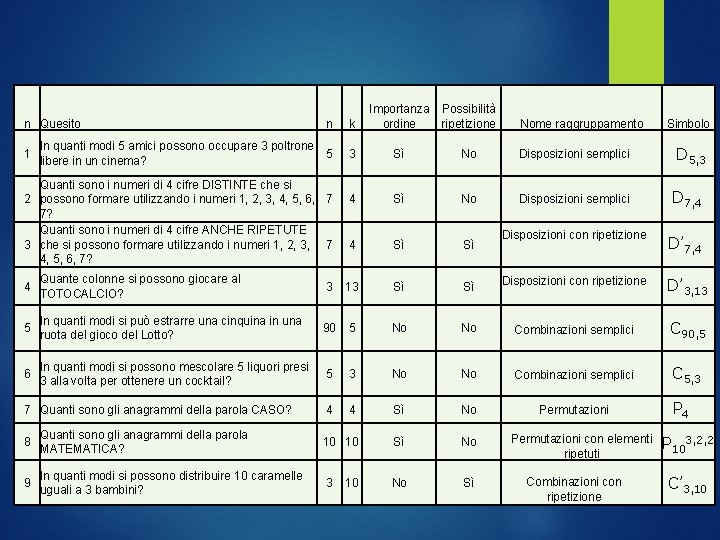
n k Importanza ordine Possibilità ripetizione In quanti modi 5 amici possono occupare 3 poltrone 5 libere in un cinema? 3 Sì No Disposizioni semplici 4 Sì No Disposizioni semplici D 7, 4 4 Sì Sì Disposizioni con ripetizione D’ 7, 4 n Quesito 1 Quanti sono i numeri di 4 cifre DISTINTE che si 2 possono formare utilizzando i numeri 1, 2, 3, 4, 5, 6, 7 7? Quanti sono i numeri di 4 cifre ANCHE RIPETUTE 3 che si possono formare utilizzando i numeri 1, 2, 3, 7 4, 5, 6, 7? Nome raggruppamento Simbolo D 5, 3 4 Quante colonne si possono giocare al TOTOCALCIO? 3 13 Sì Sì Disposizioni con ripetizione D’ 3, 13 5 In quanti modi si può estrarre una cinquina in una ruota del gioco del Lotto? 90 5 No No Combinazioni semplici C 90, 5 6 In quanti modi si possono mescolare 5 liquori presi 3 alla volta per ottenere un cocktail? 5 3 No No Combinazioni semplici C 5, 3 4 4 Sì No Permutazioni 7 Quanti sono gli anagrammi della parola CASO? 8 Quanti sono gli anagrammi della parola MATEMATICA? 10 10 Sì No 9 In quanti modi si possono distribuire 10 caramelle uguali a 3 bambini? 3 No Sì 10 Permutazioni con elementi ripetuti Combinazioni con ripetizione P 4 P 103, 2, 2 C’ 3, 10

Disposizioni semplici Dn, k Raggruppamenti di n elementi presi k alla volta nei quali l’ordine degli elementi è importante e non ci può essere ripetizione degli stessi. Esempio. Quanti numeri di tre cifre diverse si possono formare utilizzando le cifre 3, 5, 7, 9? 1 a cifra 2 a cifra 3 cifre Quante possibilità? 4 3 2 24 k elementi

Permutazioni Dn, n = Pn Raggruppamenti di n elementi che differiscono per l’ordine n 0 1 2 3 4 5 6 7 8 9 10 n! 1 1 2 6 24 120 720 5. 040 0. 320 2. 880 8. 800 numero di cifre 39. 91 1 12 1 13 1 14 2 15 3 16 3 17 4 18 5 19 6 7 6. 800 36 20 3. 62 21 n fattoriale 479. 00 9 6. 227. 02 0. 800 10 87. 178. 291. 200 11 1. 307. 674. 36 8. 000 13 20. 922. 789. 888. Per 000 14 355. 687. 428. 096. convenzione 000 15 6. 402. 373. 705. 728. 000 16 121. 645. 100. 408. 832. 000 18 2. 432. 902. 008. 176. 640. 000 19 51. 090. 942. 171. 709. 400. 000 20 1. 600 4 8

Permutazioni con elementi ripetuti Esempio. Calcolare il numero di anagrammi della parola MATEMATICA (3 A, 2 M, 2 T)

Disposizioni con ripetizione D’n, k Raggruppamenti di n elementi presi k alla volta nei quali l’ordine degli elementi è importante e ci può essere ripetizione degli stessi. Esempio. Quanti numeri di tre cifre, anche ripetute, diverse si possono formare utilizzando le cifre 3, 5, 7, 9? Quante possibilità? 4 4 Numero di colonne al Totocalcio 4

Ordine importante Disposizioni Semplici Con ripetizione Con elementi ripetuti Permutazioni

Combinazioni semplici Cn, k Raggruppamenti di n elementi presi k alla volta nei quali l’ordine degli elementi non è importante e dove non ci può essere ripetizione degli stessi. Si chiama Coefficiente binomiale Si legge n su k E’ detta legge dei 3 fattoriali Esempio. Quante cinquine possono essere estratte in una ruota del Lotto?

Combinazioni con ripetizione C’n, k Raggruppamenti di n elementi presi k alla volta nei quali l’ordine degli elementi non è importante e dove ci può essere ripetizione degli stessi. Esempio. In quanti modi si possono distribuire 10 caramelle uguali a 3 bambini?

Ordine non importante Combinazioni Semplici Con ripetizione

Riepilogo Raggruppamenti di calcolo combinatorio Ordine importante Disposizioni Semplici Con ripetizione Con elementi ripetuti Permutazioni Ordine non importante Combinazioni