CALCOLO COMBINATORIO INDICE Che cos il calcolo combinatorio

CALCOLO COMBINATORIO

INDICE • Che cos’è il calcolo combinatorio? • Concetto di raggruppamenti semplici e di raggruppamenti con ripetizione • Disposizioni • Combinazioni • Permutazioni

PROBLEMI 1. In quanti modi diversi 3 ragazzi di una compagnia di 5 amici si possono sedere su 3 poltrone libere di un cinema? 2. Quanti numeri di 4 cifre si possono comporre con le cifre 1, 2, 3, 4, 5, 6? 3. Quanti anagrammi si possono comporre con le lettere della parola ROMA? E con la parola ALA? 4. Quanti terni si possono fare con i 90 numeri del Lotto? 5. In quanti modi diversi 7 caramelle identiche possono essere distribuite tra 4 bambini? E se le caramelle fossero diverse? DS DR PS PR CS CR

CHE COS’E’? Il calcolo combinatorio è un particolare ramo della matematica applicata avente come scopo la costruzione e la misurazione del numero di raggruppamenti diversi che si possono comporre prendendo una determinata quantità di elementi in un assegnato insieme, in modo che siano rispettate determinate regole. VEDI ESEMPI

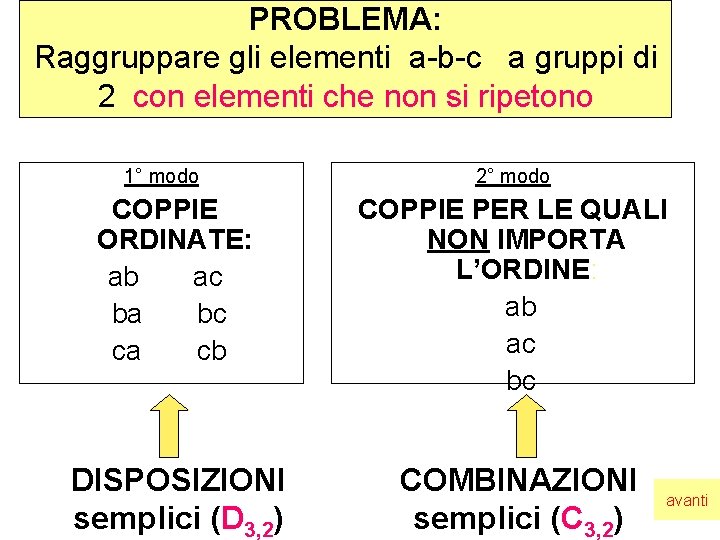
PROBLEMA: Raggruppare gli elementi a-b-c a gruppi di 2 con elementi che non si ripetono 1° modo 2° modo COPPIE ORDINATE: ab ac ba bc ca cb COPPIE PER LE QUALI NON IMPORTA L’ORDINE: ab ac bc DISPOSIZIONI semplici (D 3, 2) COMBINAZIONI semplici (C 3, 2) avanti

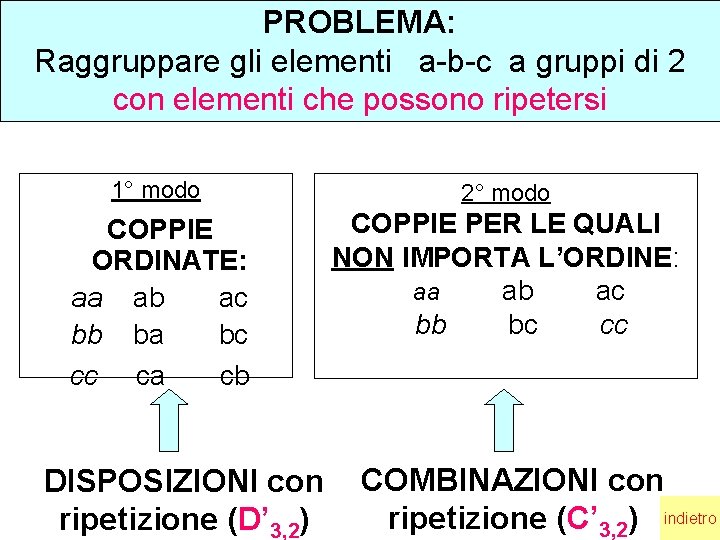
PROBLEMA: Raggruppare gli elementi a-b-c a gruppi di 2 con elementi che possono ripetersi 1° modo 2° modo COPPIE ORDINATE: aa ab ac bb ba bc cc ca cb COPPIE PER LE QUALI NON IMPORTA L’ORDINE: aa ab ac bb bc cc DISPOSIZIONI con ripetizione (D’ 3, 2) COMBINAZIONI con ripetizione (C’ 3, 2) indietro

I RAGGRUPPAMENTI POSSONO ESSERE: • SEMPLICI: quando gli oggetti sono tutti diversi • CON RIPETIZIONE: quando gli oggetti vi figurano una o più volte

“NOMI” DEI RAGGRUPPAMENTI DISPOSIZIONI: quando l’ordine degli elementi è importante. COMBINAZIONI: quando l’ordine degli elementi non ha alcuna importanza.

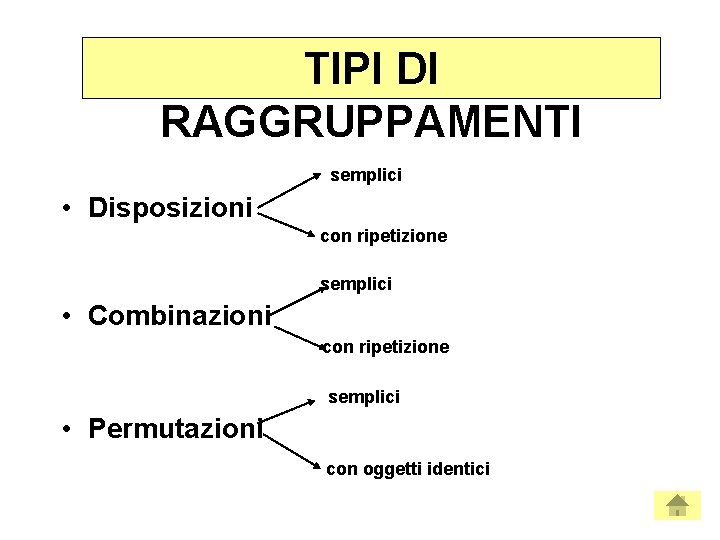
TIPI DI RAGGRUPPAMENTI semplici • Disposizioni con ripetizione semplici • Combinazioni con ripetizione semplici • Permutazioni con oggetti identici

COME CALCOLARE IL NUMERO DI DISPOSIZIONI?

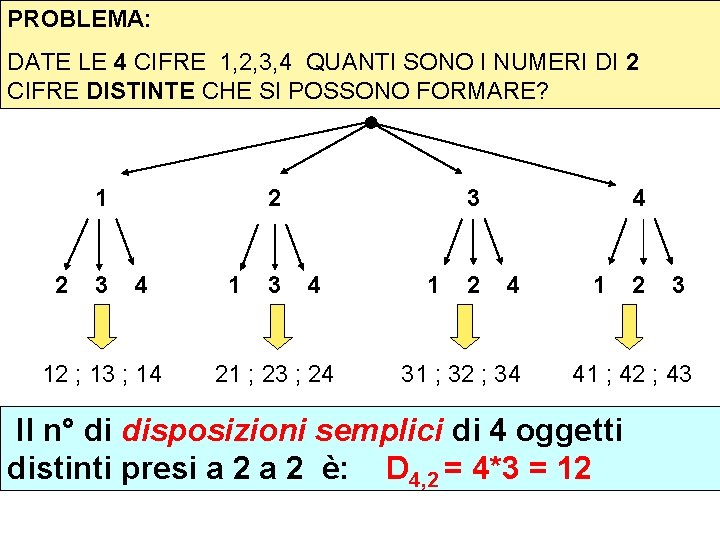
PROBLEMA: DATE LE 4 CIFRE 1, 2, 3, 4 QUANTI SONO I NUMERI DI 2 CIFRE DISTINTE CHE SI POSSONO FORMARE? 1 2 3 2 4 12 ; 13 ; 14 1 3 3 4 21 ; 23 ; 24 1 2 4 4 31 ; 32 ; 34 1 2 3 41 ; 42 ; 43 Il n° di disposizioni semplici di 4 oggetti distinti presi a 2 è: D 4, 2 = 4*3 = 12

IN GENERALE: il n° di DISPOSIZIONI SEMPLICI di n oggetti distinti presi k per volta è Dn, k= n(n-1)(n-2) …. . (n-k+1) con n>k (cioè il prodotto di k numeri naturali PROBLEMI

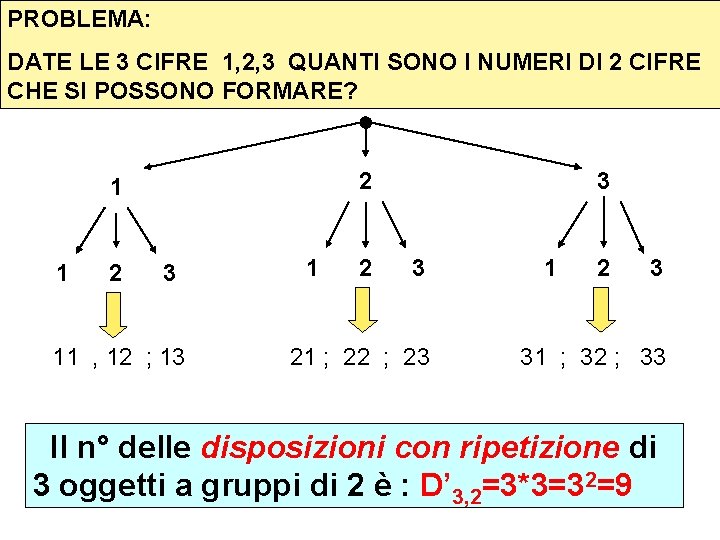
PROBLEMA: DATE LE 3 CIFRE 1, 2, 3 QUANTI SONO I NUMERI DI 2 CIFRE CHE SI POSSONO FORMARE? 2 1 1 2 3 11 , 12 ; 13 1 2 3 3 21 ; 22 ; 23 1 2 3 31 ; 32 ; 33 Il n° delle disposizioni con ripetizione di 3 oggetti a gruppi di 2 è : D’ 3, 2=3*3=32=9

IN GENERALE: il n° delle DISPOSIZIONI CON RIPETIZIONE di n oggetti distinti presi k per volta è D’n, k= k n PROBLEMI

COME CALCOLARE IL NUMERO DI COMBINAZIONI?

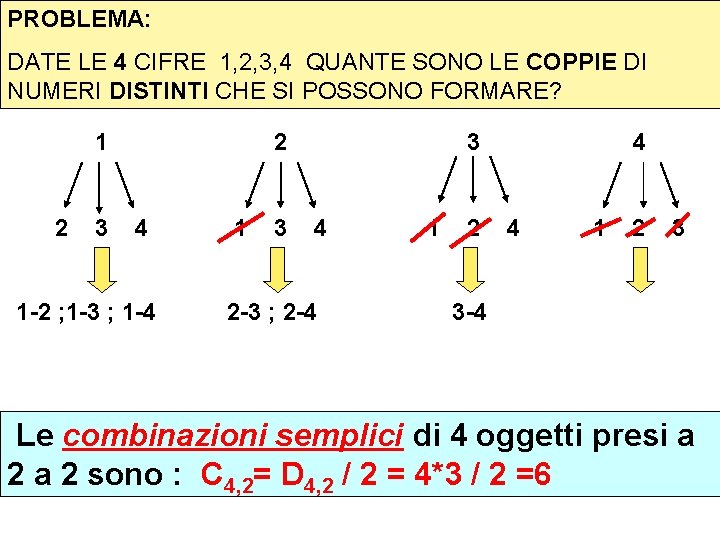
PROBLEMA: DATE LE 4 CIFRE 1, 2, 3, 4 QUANTE SONO LE COPPIE DI NUMERI DISTINTI CHE SI POSSONO FORMARE? 1 2 3 2 4 1 -2 ; 1 -3 ; 1 -4 1 3 3 4 2 -3 ; 2 -4 1 2 4 4 1 2 3 3 -4 Le combinazioni semplici di 4 oggetti presi a 2 sono : C 4, 2= D 4, 2 / 2 = 4*3 / 2 =6

IN GENERALE: il n° di COMBINAZIONI SEMPLICI di n oggetti distinti presi k per volta è Cn, k = Dn, k / k! = ( n k ) con n>k PROBLEMI

PROBLEMA: DATE LE 2 LETTERE a, b QUANTE SONO LE COMBINAZIONI CON RIPETIZIONE DI TALI OGGETTI PRESI A 3? aaa aab abb bbb Il n° di combinazioni con ripetizione di n oggetti distinti presi a 3 è : C’ 2, 3= ( ) = ( 3) = 4 2+3 -1 3 4

IN GENERALE: il n° delle COMBINAZIONI CON RIPETIZIONE di n oggetti distinti presi k per volta è C’n, k= n(n+1)…. . (n+k-1) K! (cioè è il prodotto di k fattori crescenti a partire da n, diviso k! ) PROBLEMI

CHE COSA SONO LE PERMUTAZIONI?

PERMUTAZIONI SEMPLICI ESEMPIO: COSTRUIRE E CONTARE GLI ANAGRAMMI (anche privi di senso) DELLA PAROLA APE P E APE E P AEP A E PAE E A PEA A P EAP P A EPA A P E Il n° delle permutazioni di 3 oggetti distinti è: P 3 = D 3, 3 = 3*2*1 = 6

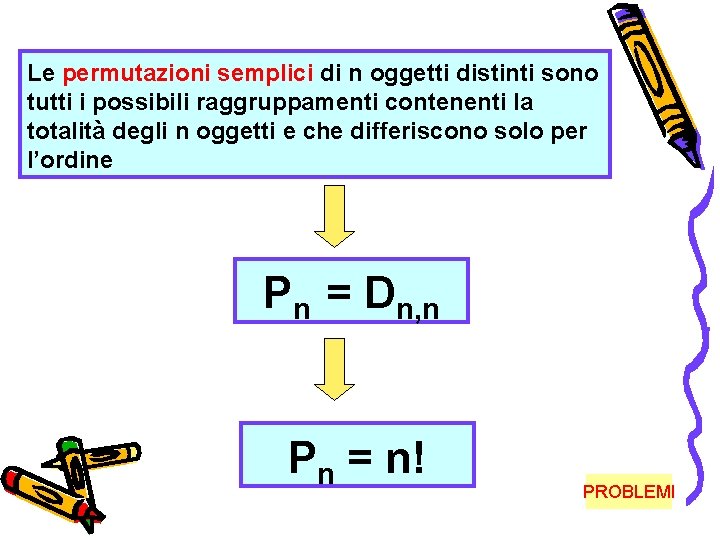
Le permutazioni semplici di n oggetti distinti sono tutti i possibili raggruppamenti contenenti la totalità degli n oggetti e che differiscono solo per l’ordine Pn = Dn, n Pn = n! PROBLEMI

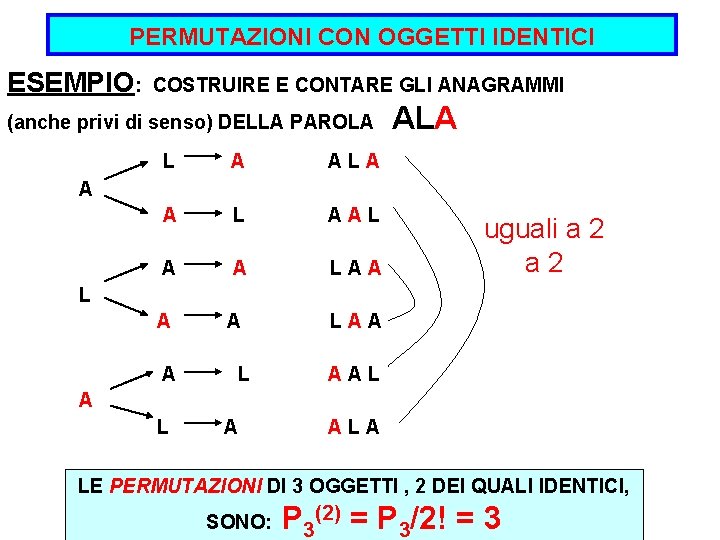
PERMUTAZIONI CON OGGETTI IDENTICI ESEMPIO: COSTRUIRE E CONTARE GLI ANAGRAMMI (anche privi di senso) DELLA PAROLA L A ALA A L AAL A A LAA ALA A uguali a 2 L AAL A ALA LE PERMUTAZIONI DI 3 OGGETTI , 2 DEI QUALI IDENTICI, SONO: P 3(2) = P 3/2! = 3

IN GENERALE: se tra gli n oggetti dati ve ne sono α uguali tra loro, β uguali tra loro… il numero delle permutazioni degli n oggetti assegnati risulta: Pn(α, β ) = n! α! * β! PROBLEMI

E ora risolviamo i problemi formulati all’inizio della presentazione !!!!!