HALMAZOK A HALMAZ S MEGADSA A HALMAZ FOGALMA

*** HALMAZOK *** A HALMAZ ÉS MEGADÁSA A HALMAZ FOGALMA Magát a halmaz fogalmát nem definiáljuk, ugyanúgy mint ahogyan a "pontra", vagy a geometriai "egyenesre" sem adunk meghatározást. Elfogadjuk. Tetszőleges dolgok (objektumok) összességét halmaznak tekintjük; a "halmaz„ szó mintegy szinonimája a köznyelvben használt "összesség", "sokaság" stb. kifejezéseknek. Az összességbe tartozó egyes dolgok a halmaz elemei. 1

Ha adott egy H halmaz, és annak h egy eleme, akkor ezt így jelöljük: Ha az jelet áthúzzuk, azaz -t írunk, az azt jelenti, hogy nem eleme a halmaznak. Venn-diagram: Üres halmaz: . 2

HALMAZ ÉS RÉSZHALMAZA Tulajdonságok: (reflexivitás) (antiszimmetria) (tranzitivitás) Valódi részhalmazok. Példa. Legyen K = {egész számok}; H = {páratlan egész számok}. Nyilván 3

P(H): egy H halmaz hatványhalmaza. n elemű halmaznak 2 n részhalmaza van. Példa. Legyen H ={a, b, c}, akkor P(H) = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}. Alaphalmaz. X-szel jelöljük. MŰVELETEK HALMAZOKKAL Egyesítés (jele: ). A H és K halmazok egyesítése (összege vagy uniója) : H K = {x|x H vagy x K. Metszet (jele: ). A H és K halmazok metszete (közös része, vagy szorzata): H K = {x|x H és x K}. 4

Azonosságok: H H = H (idempotencia) H K = K H (kommutativitás) H (K L)=(H K) L (asszociativitás) Megjegyzés. Ha H K = , H és K diszjunktak vagy idegenek. Különbség (jele: – ). A H és K halmazok különbsége: H – K = {x| x H és x K}. 5

Azonosságok: 1. H - K H 2. (H - K) K = 3. H - K = H, akkor és csak akkor, ha H K= Halmaz komplementere. X – K halmaz a K kiegészítő (komplementer) halmaza. Példa. A = {a, b, c, d, e}, X={a magyar ábécé betűi}. = {a magyar ábécé betűi az a, b, c, d, e betűk kivételével}. 6

Azonosságok: 7

RELÁCIÓK RENDEZETT n-ESEK Rendezett pár. z=(x, y) Rendezett pár transzponáltja: (x, y) (y, x). u = (x, y) és v = (a, b). u=v x=a és y=b. Rendezett n-es. (a 1, a 2, . . . , an)-nel jelöljük. (a 1, a 2, . . . , an)=(b 1, b 2, . . . , bn) a 1 = b 1, a 2=b 2, . . . , an= bn. Példák. 1. A sík pontjainak koordinátái. 2. Rendezett hármas a (Kovács, István, 14112250138). 3. Rendezett "n-es" egy család (hármas, négyes, stb, pl. : apa, anya, gyerek 1, gyerek 2). 8

HALMAZOK DIREKT SZORZATA DEFINÍCIÓ. A és B direkt szorzata: A B (A kereszt B), (x, y) A B x A és y B. 1. Példa. Ha A = {a, b, c} és B = {x, y}, akkor A B={(a, x), (b, x), (c, x), (a, y), (b, y), (c, y)}. B A={(x, a), (x, b), (x, c), (y, a), (y, b), (y, c)}. Látható, hogy A B B A. 2. Példa. Ha V a vezeték- , K a keresztnevek, A az adószámok halmaza, akkor (Kovács, István, 14112250138) V K A egy eleme. Megjegyzés. Descartes-szorzat elnevezés. 9

Megjegyzés. A direkt szorzatra érvényesek az alábbi tulajdonságok. 1. 2. 3. 4. Több halmaz direkt szorzata is képezhető. Példa. Legyen R a valós számok halmaza. Az R R szorzat nyilván a síkbeli koordinátarendszer pontjait adja. 10

RELÁCIÓK DEFINÍCIÓ. Az A 1, A 2, . . . , An halmazok A 1 A 2 . . . An direkt szorzatának egy részhalmazát n-változós relációnak nevezzük és R-rel jelöljük, azaz R A 1 A 2 . . . An. A reláció tehát rendezett n-esek halmaza. Ai -t a reláció i-edik tartományának nevezzük. 11

név (N), születési-dátum (D), matematikaosztályzat (M). N D M Relációs adatbázis. 12

BINÉR RELÁCIÓK Jele: a. Rb. PÉLDÁK 1. Példa. Binér reláció a számok közötti egyenlőség, a kisebb, a nagyobb reláció azaz: a = b, a < b, a > b. 2. Példa. x. Ry: "x szülője y-nak” 3. Példa. p | a: "p osztója a-nak” Az x. Ry reláció értelmezési tartománya az {x} halmaz, képtartománya az {y} halmaz. 13

Reláció inverze: x. Ry inverze y. R’x. PÉLDÁK inverz relációra: 1. Ha az R a "szülője" reláció, akkor R' a "gyermeke” kapcsolatot fejezi ki. 2. A kisebb reláció inverze a nagyobb: a < b b > a. 3. Az = reláció inverze önmaga, mivel x=y y=x. A binér reláció tulajdonságai: . 1. R reláció reflexív: ha x. Rx. Ha nem, irreflexív. Példa. A reláció reflexív, mert x x. A < reláció irreflexív, mert x < x nem teljesül. 14

2. R szimmetrikus, ha x. Ry y. Rx, ellenkező esetben aszimmetrikus. Ha x. Ry és y. Rx x=y, akkor antiszimmetrikus. Példa. Az = reláció szimmetrikus, hiszen x=y ugyanaz mint y= x. (antiszimmetrikus is. ) 3. R tranzitív, ha x. Ry, y. Rz x. Rz. Példa. A < reláció tranzitív. (a<b, b<c a<c) EKVIVALENCIA ÉS RENDEZÉS a) Ekvivalencia Egy X alaphalmaz elemei közt értelmezett R relációt ekvivalencia-relációnak nevezünk, ha R reflexív, szimmetrikus és tranzitív. Jelölése: x ~ y. 15

Tulajdonságai: 1. x ~ x 2. (x ~ y) (y ~ x) 3. (x ~ y és y ~ z) (x ~ z) Példák. 1. A valós számok körében értelmezett egyenlőség. a) a=a b) a=b b=a c) a=b, b=c a=c 2. Ha egy ház lakóinak halmazát H-val jelöljük, akkor az "x ugyanabban a házban lakik, mint y” 16

Egy X alaphalmaz elemei közt értelmezett R relációt akkor mondunk parciális (vagy részben) rendezési relációnak, ha R reflexív, antiszimmetrikus és tranzitív. Jelölése: x y. (olv. x megelőzi y-t) 1) x x; 2) (x y és y x) (x =y) 3) (x y és y z) (x z) 17

PÉLDÁK 1. Példa. A természetes számok N halmazában az oszthatóság rendezési reláció. 2. Példa. Egy X halmaz részhalmazainak halmaza: P(X). A tartalmazás binér relációja nyilván rendezési reláció. 3. Példa. Legyen N a természetes számok halmaza. Ez a halmaz a " " relációval rendezett halmaz: N ={1, 2, 3, 4, . . . }. Megjegyzés. A bináris relációk, mint halmazok között elvégezhetők a szokásos halmazműveletek. Legyenek R 1 és R 2 bináris relációk. Akkor szintén bináris relációk. 18

FÜGGVÉNYEK A FÜGGVÉNY FOGALMA DEFINÍCIÓ. Legyen az f reláció első tartománya X, második tartománya Y, és tegyük fel, hogy minden x X-hez pontosan egy olyan y Y létezik, melyre xfy. Ekkor f minden X-beli x elemhez egy jól meghatározott y Y elemet rendel. Jelöljük ezt az y-t f(x)-szel, azaz y = f(x). Az ilyen relációkat X-ből Y-ba képező függvényeknek vagy leképezéseknek nevezzük. 19

X: f értelmezési tartománya, jele: Df Y: f képtere (értékkészlete), jele: Rf f függvény: f : x y, vagy x y Az x elemhez tartozó értéket f(x)-szel jelöljük, és azt mondjuk, hogy f(x) az x elem képe. f X Y 20

AZ ÖSSZETETT FÜGGVÉNY DEFINÍCIÓ. f: X Y, és g: Y Z két függvény. és z Z és létezik olyan y Y, hogy y=f(x), z=g(y)}. Tegyük fel, hogy Rf Dg. A g f reláció egy függvény és összetett függvénynek hívjuk. A függvény grafikonja Jelölje f(X) az X-beli elemek képeinek halmazát Y-ban. Nyilvánvalóan f(X) Y. Legyen f: X Y és legyen X’ részhalmaza X-nek, azaz legyen X’ X. Akkor az {f(x)|x X’} halmazt az f grafikonjának nevezzük. 21

A FÜGGVÉNY INVERZE Ha az f függvény olyan, hogy különböző elemek képe különböző, azaz xl x 2 esetén f(xl) f(x 2), akkor azt mondjuk, hogy az f függvény injektív. DEFINÍCIÓ. Ha f injektív leképezés, akkor az f(X) képhalmaz minden y eleméhez egyértelműen hozzá tudjuk rendelni az y egyetlen ősképét, vagyis az egyetlen olyan x X elemet, melyre f(x)=y. Így egy újabb leképezést nyerhetünk, melynek értelmezési tartománya f(X), képtere pedig X. Ez a függvény az f inverze, és f -1 -gyel jelöljük. 22

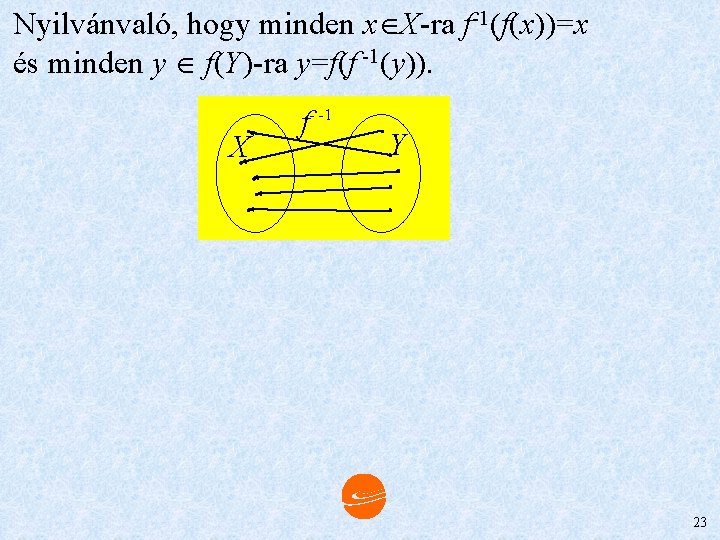
Nyilvánvaló, hogy minden x X-ra f-1(f(x))=x és minden y f(Y)-ra y=f(f -1(y)). X f- -1 Y 23