Diszjunkt halmazok adatszerkezete A diszjunkt halmaz adatszerkezet diszjunkt

Diszjunkt halmazok adatszerkezete • A diszjunkt halmaz adatszerkezet diszjunkt dinamikus halmazok S={S 1, …, Sn} halmaza. • Egy halmazt egy képviselője azonosít • Megvalósítás pl. láncolt listákkal • Halmazt. Készít(x): Képviselő egy olyan új halmazt hoz létre, amely egyetlen eleme x. X nem lehet eleme egyetlen más halmaznak sem • Egyesít(x, y): Képviselő az x-et tartalmazó Sx és az yt tartalmazó Sy halmazokat egyesíti • Halmazt. Keres(x): Képviselő visszaadja azon halmaz képviselőjének a mutatóját, amelynek x egy eleme

Mohó algoritmusok • • Optimalizációs problémák Globális lokális optimalizálás A mohó stratégia csak helyi optimalizálást végez Bizonyos problémákra bebizonyíthatóan (globálisan is) optimális eredményt ad • Más problémákra csak szuboptimális a mohó eredmény • Példa: erőforrás lefoglalási probléma. Tfh adott egy S=(S 1, …, Sn) eseményhalmaz, amelyekhez egy ki kezdő és egy bi befejező időpont rendelhető. Két esemény kompatibilis, ha a kezdő vagy befejező pillanatukon kívül nincs átfedő időpillanat. Az optimálás célja: minél több (rövid) eseményt rendeljünk az erőforráshoz.

• Az algoritmus lényege: 1. a versenyző eseményeket a befejező időpont szerint rendezzük 2. vesszük a legkorábban befejeződőt (a legrövidebbet) 3. ciklusban vesszük a befejeződött esemény után leghamarabb kezdődő (és a sorban a leghamarabb befejeződőt) • A mohó stratégiát a sorbaállítás és a leghamarabb befejeződő esemény kiválasztása jelenti. • Ez esetben a mohó (lokálisan optimális) megoldás választása egyben globálisan is optimális megoldást ad.

Gráfalgoritmusok – Optimális feszítőfa • Súlyozott gráfok: az élekhez hozzárendelt w: E R függvény. • Def: egy G irányítatlan gráf feszítőfája: egy olyan fa, amely az eredeti csomóponthalmazából, és az élek egy részhalmazából áll. • Minimális: az élek minimális (súlyú) részhalmazából áll • Mind a mélységi, mind a széltében keresés létrehoz egy feszítőfát (feszítő erdőt). • Prim és Kruskal algoritmusa (mohó algoritmusok) • Példa: a fa teljes súlya 37. Figyeld az ah bc cserét! b 4 a 8 11 8 7 i h 1 c 2 d 7 4 14 6 g 2 9 f e 10 Vágat

Minimális feszítőfa növelése • Alapötlet: valamelyik csúcspontból kiindulva élenként növelve. Nyilvántartjuk a minimális feszítőfa eddig felderített részét. • Mohó stratégia: lépésenként egy „optimálisnak látszó” élt választunk ki. • Azt az élt, amelyet a felderített fához hozzáveszünk, biztonságos élnek nevezzük, ha a fa még mindig optimális marad. • Def: egy gráf egy vágata a csúcspontjainak két halmazba osztása. Léteznek a vágatot keresztező és kikerülő élek. • Def: Egy vágatban könnyű élnek nevezzük a legkevesebb súlyúakat.

Általános Minimális. Feszítőfa. Növelő algoritmus pszeudokódja • Min. FFa={} while FFa nem feszítőfa keresünk egy biztonságos (u, v) élt FFa-ra nézve FFa=FFa+{(u, v)} Return FFa • Tétel: Ha G=(V, E) a w: E R függvénnyel súlyozott gráf, és A olyan részhalmaza E-nek, ami egy minimális feszítőfa része is. Ha (u, v) egy könnyű él a FFa-t kikerülő vágatban, akkor az biztonságos is FFa-ra nézve • Biz…. . Nem bizonyítjuk be • Vagyis: a mohó algoritmus egyben globálisan optimális is

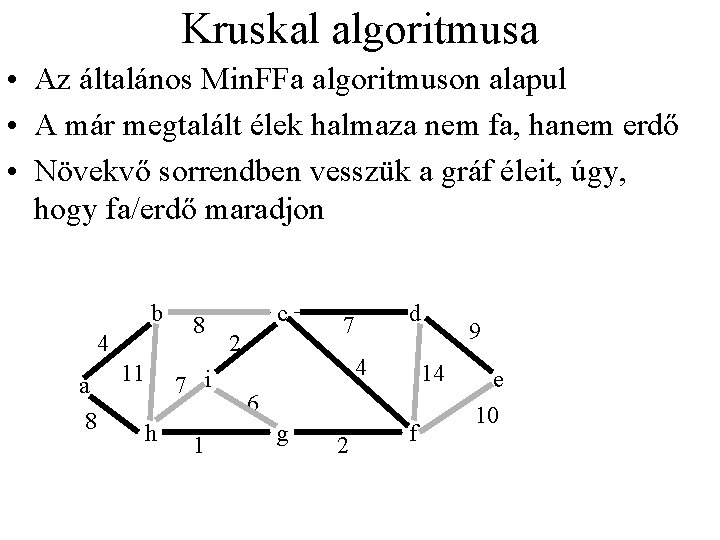
Kruskal algoritmusa • Az általános Min. FFa algoritmuson alapul • A már megtalált élek halmaza nem fa, hanem erdő • Növekvő sorrendben vesszük a gráf éleit, úgy, hogy fa/erdő maradjon b 4 a 8 11 8 7 i h 1 c 2 d 7 4 14 6 g 2 9 f e 10

Kruskal algoritmusa • Min. FFa. Kruskal FFa={} for minden uÎV-re do Halmazt. Készít(u) Élek rendezése súly szerint növekvő sorrendben for minden (u, v)ÎE élre növekvő sorrendben do if Halmazt. Keres(u)<>Halmazt. Keres(v) then FFa=FFa+{(u, v)} Egyesít(u, v) return FFa • Futási idő: elsősorban a diszjunkt halmaz megvalósítástól függ. Megfelelő megvalósítás esetén O(|E|*log(|E|))

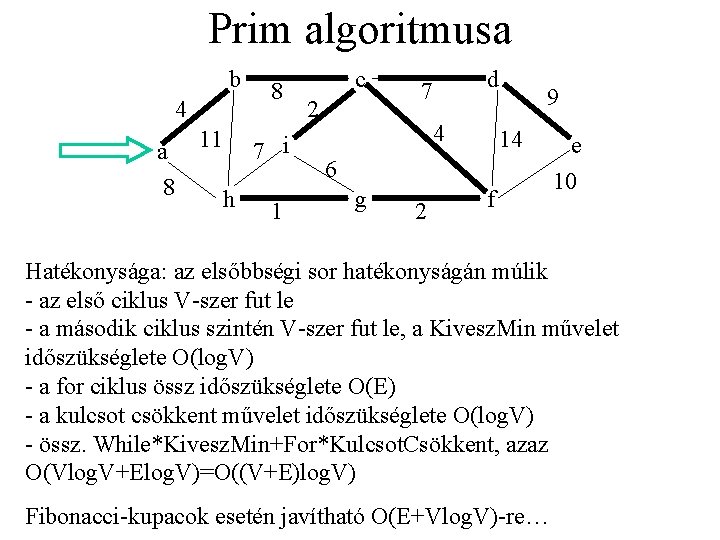
Prim algoritmusa • Egyetlen gyökérpontból indul ki, egyetlen fát épít • Kezdetben a bejáratlan csúcsok V, az induló csúcs súlya pedig 0 • Minden lépésben a még bejáratlan legkönnyebb élt vesszük hozzá a halmazhoz. • A bejáratlan csomópontokat prioritásos sorban tároljuk, amely a kulcs tulajdonság szerint van sorbaállítva (az odavezető él súlya) • Ha egy csúcsot már elértünk, és az új irányból könnyebb élt találunk, akkor lecseréljük a kulcs értékét és a Szülő értéket • Az eredmény a Szülő vektorban tárolt fa lesz

Prim algoritmusa b 4 a 8 11 8 7 i h 1 c 2 d 7 4 9 14 6 g 2 f e 10 Hatékonysága: az elsőbbségi sor hatékonyságán múlik - az első ciklus V-szer fut le - a második ciklus szintén V-szer fut le, a Kivesz. Min művelet időszükséglete O(log. V) - a for ciklus össz időszükséglete O(E) - a kulcsot csökkent művelet időszükséglete O(log. V) - össz. While*Kivesz. Min+For*Kulcsot. Csökkent, azaz O(Vlog. V+Elog. V)=O((V+E)log. V) Fibonacci-kupacok esetén javítható O(E+Vlog. V)-re…

• Min. FFAPrim(r) Bejáratlan=V for minden vÎV-re do kulcs[v]=végtelen kulcs[r]=0 Szülő[r]=NIL while Bejáratlan<>{} do u=Bejáratlan. Kivesz. Min for minden vÎu. Szomszéd-ra do if vÎBejáratlan and w(u, v)<=kulcs[v] then Szülő[v]=u kulcs[v]=w(u, v) return Szülő