Graph homomorphisms statistical physics and quasirandom graphs Lszl

Graph homomorphisms, statistical physics, and quasirandom graphs László Lovász Microsoft Research lovasz@microsoft. com Joint work with: Christian Borgs, Jennifer Chayes, Mike Freedman, Jeff Kahn, Lex Schrijver, Vera T. Sós, Balázs Szegedy, Kati Vesztergombi

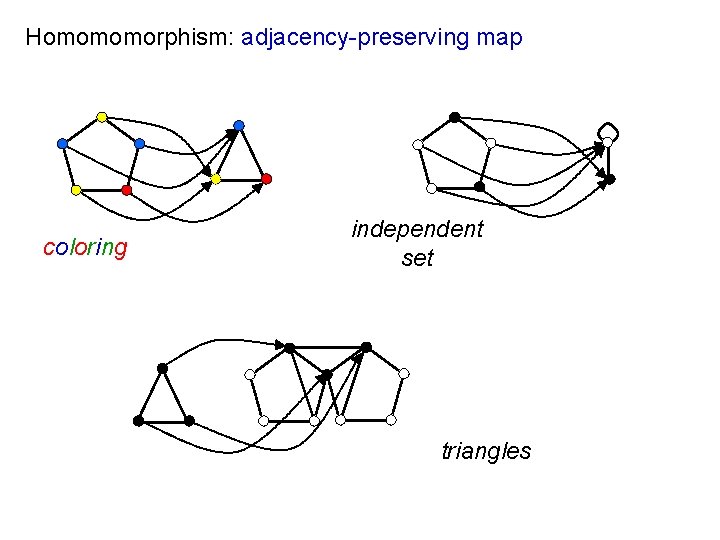
Homomomorphism: adjacency-preserving map coloring independent set triangles

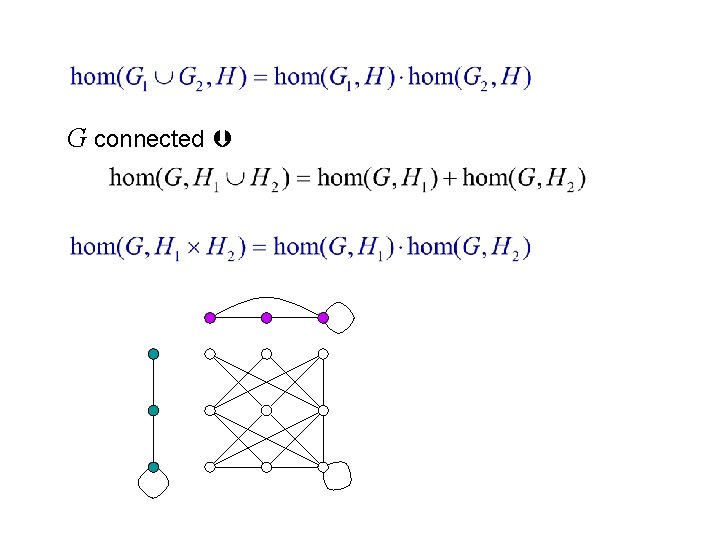
Weighted version:

G connected

L 1966

Homomorphism density: probability that random map is a homomorphism every node in G weighted by 1/|V(G)| Homomorphism entropy:

Examples: if G has no loops

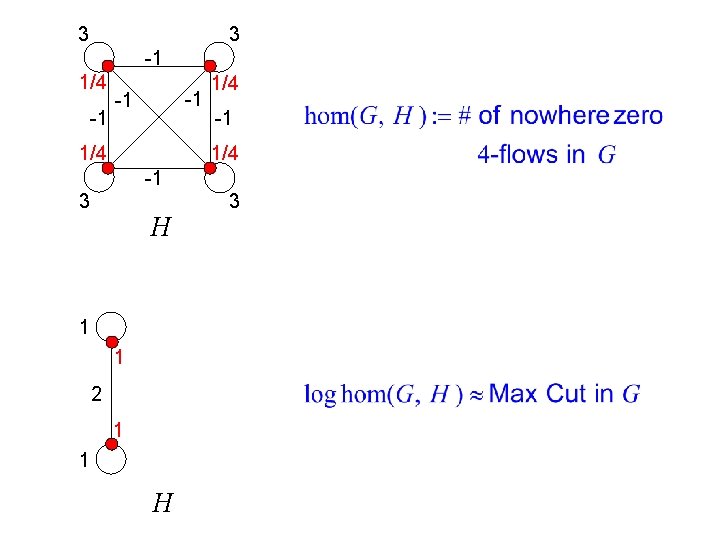
3 3 -1 1/4 -1 -1 -1 1/4 -1 3 H 1 1 2 1 1 H 3

Hom functions and statistical physics atoms are in states (e. g. up or down): interaction only between neighboring atoms: graph G energy of interaction: energy of state: partition function:

partition function: sparse G bounded degree All weights in H are 1 hard-core model H=Kq, all weights are positive soft-core model dense G

Recall: : set of connected graphs Erdős – Lovász – Spencer

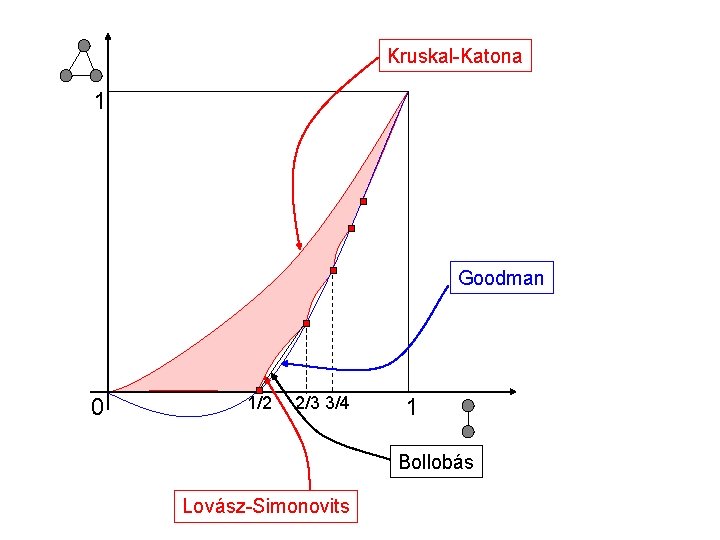
Kruskal-Katona 1 Goodman 0 1/2 2/3 3/4 1 Bollobás Lovász-Simonovits

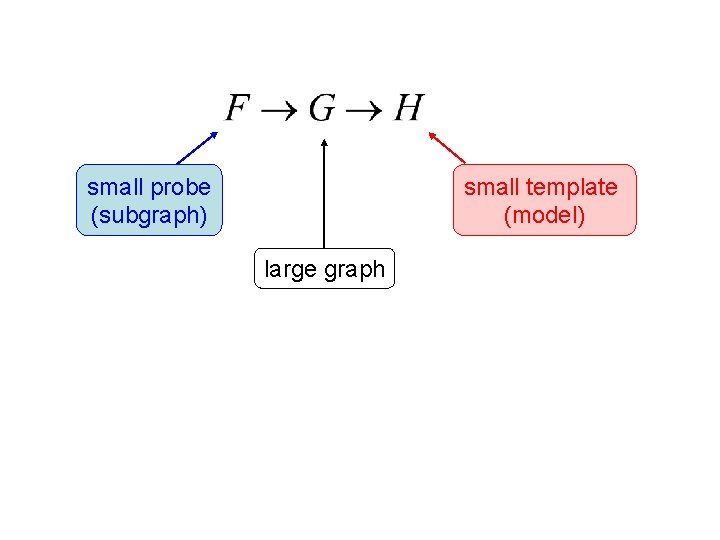
small probe (subgraph) small template (model) large graph

Turán’s Theorem for triangles: Kruskal-Katona Theorem for triangles: Erdős’s Theorem on quadrilaterals:

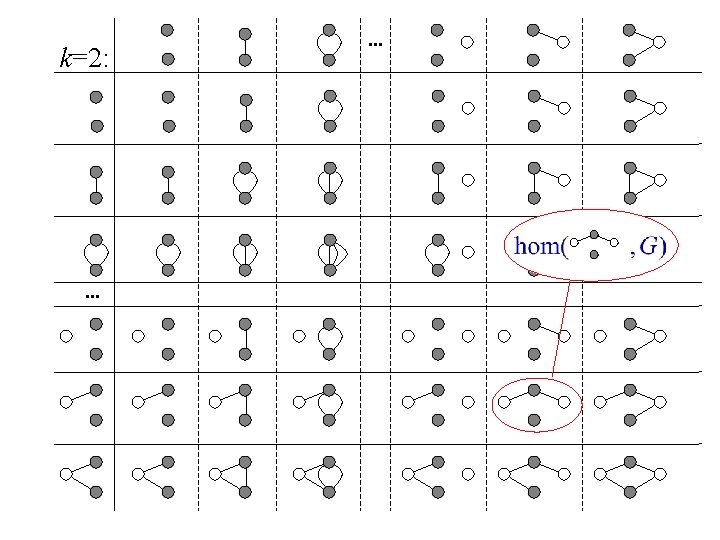
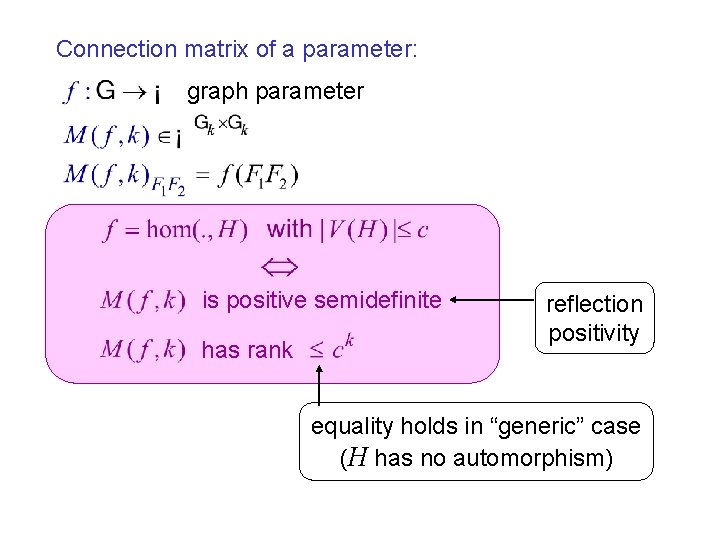
Connection matrices k-labeled graph: k nodes labeled 1, . . . , k Connection matrix (for target graph G):

Main Lemma: is positive semidefinite has rank reflection positivity

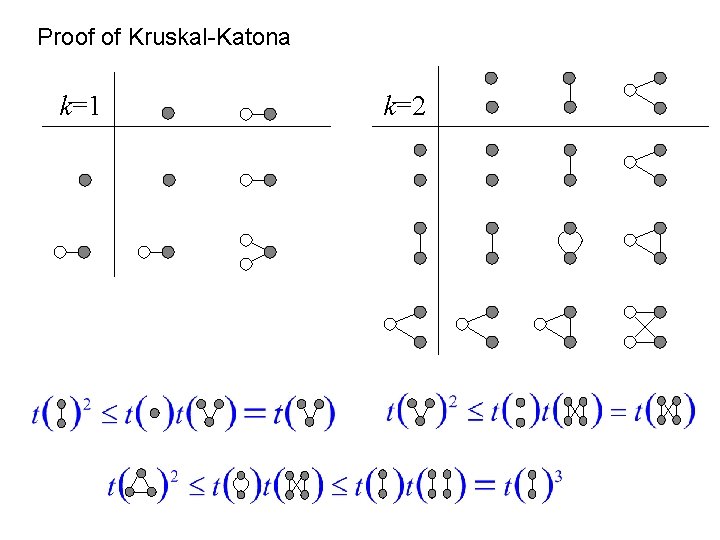
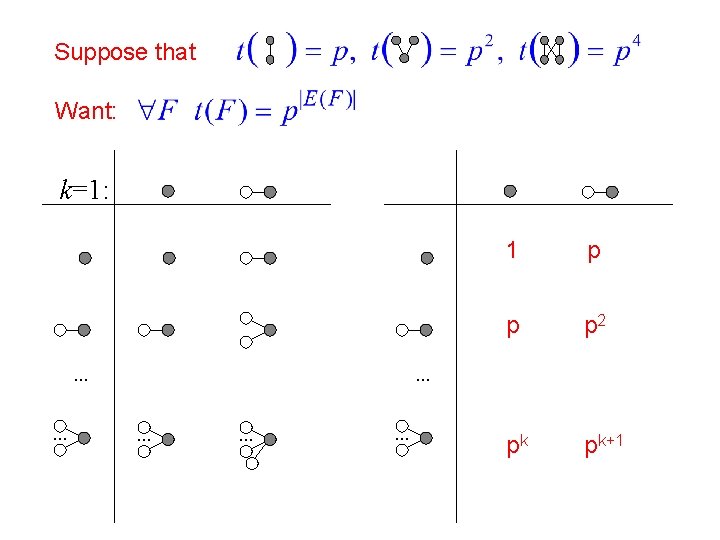
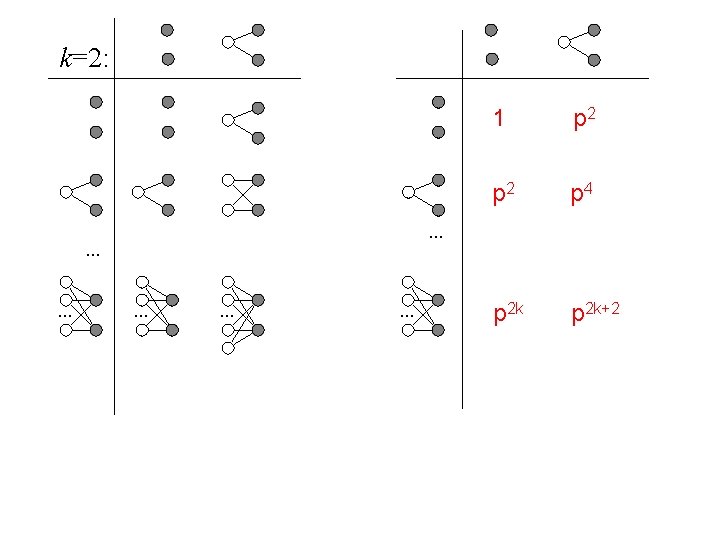
Proof of Kruskal-Katona k=1 k=2

How much does the positive semidefinite property capture? . . . almost everything!

Connection matrix of a parameter: graph parameter is positive semidefinite has rank reflection positivity equality holds in “generic” case (H has no automorphism)

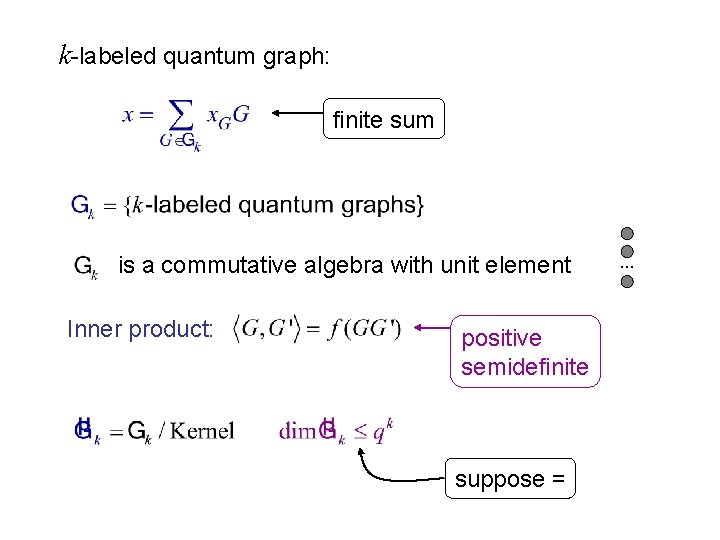
k-labeled quantum graph: finite sum is a commutative algebra with unit element Inner product: positive semidefinite suppose = . . .

Distance of graphs: Converse? ? ?

Quasirandom graphs Thomason Chung – Graham – Wilson (Gn: n=1, 2, . . . ) is quasirandom, if d(Gn, G(n, p)) 0 a. s. Example: Paley graphs p: prime 1 mod 4 How to see that these graphs are quasirandom?

For a sequence (Gn: n=1, 2, . . . ), the following are equivalent: (Gn) is quasirandom; simple graph F; for F=K 2 and C 4. Chung – Graham – Wilson Converse if G’ is a random graph.

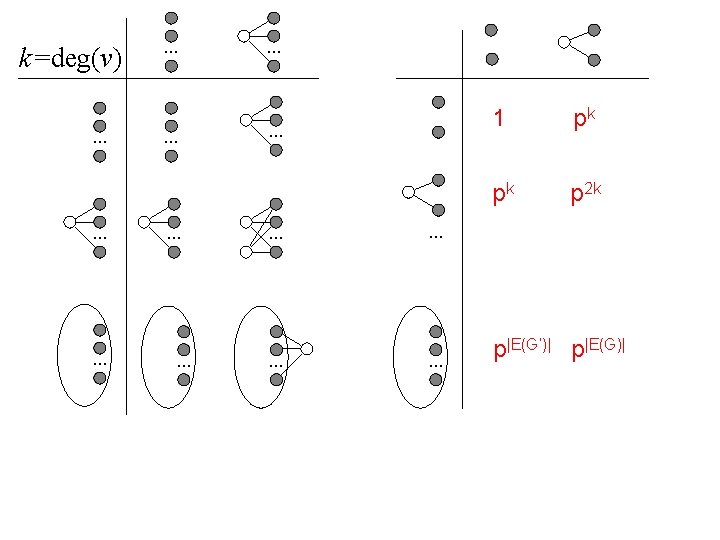
Suppose that Want: k=1: . . . 1 p p p 2 pk pk+1 . . .

k=2: p 2 p 4 p 2 k+2 . . 1 . .

k=deg(v). . . . 1 pk pk p 2 k . . . p|E(G’)| p|E(G)|

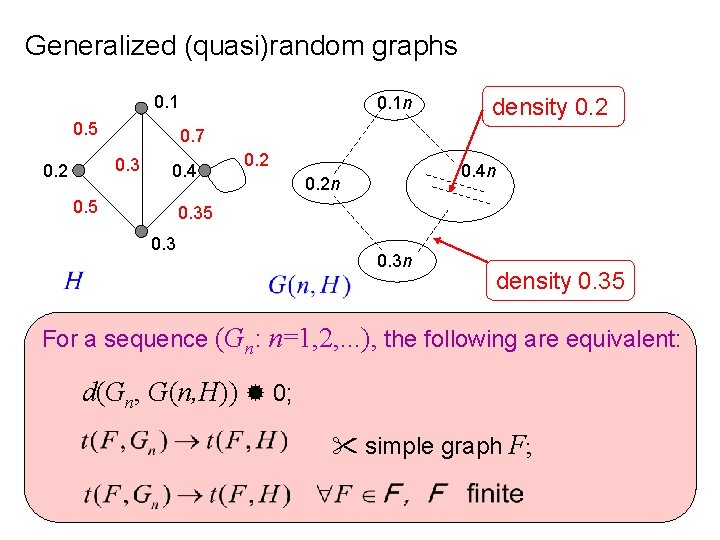
Generalized (quasi)random graphs 0. 1 0. 5 density 0. 2 0. 7 0. 3 0. 2 0. 1 n 0. 4 0. 5 0. 2 0. 4 n 0. 2 n 0. 35 0. 3 n density 0. 35 For a sequence (Gn: n=1, 2, . . . ), the following are equivalent: d(Gn, G(n, H)) 0; simple graph F;

Recall: (Gn) left-convergent: (Gn) right-convergent:

Example: (C 2 n) is right-convergent But. . . (Cn) is not convergent for bipartite H

Any connection between left and right convergence?

Graphs with bounded degree D (Gn) left-convergent: e. g. H=Kq, q>8 D