Section 13 Homomorphisms Definition A map of a

Section 13 Homomorphisms Definition A map of a group G into a group G’ is a homomorphism if the homomophism property (ab) = (a) (b) Holds for all a, b G. Note: The above equation gives a relation between the two group structures G and G’. Example: For any groups G and G’, there is always at least one homomorphism: : G G’ defined by (g)=e’ for all g G, where e’ is the identity in G’. We call it the trivial homomorphism.

Examples Example Let r Z and let r: Z Z be defined by r (n)=rn for all n Z. Is r a homomorphism? Solution: For all m, n Z, we have r(m + n) = rm + rn = r (m)+ r (n). So r is a homomorphism. Example: Let : Z 2 Z 4 Z 2 be defined by (x, y)=x for all x Z 2, y Z 4. Is a homomorphism? Solution: we can check that for all (x 1, y 1), (x 2, y 2) Z 2 Z 4, ((x 1, y 1)+(x 2, y 2) )= x 1+ x 2= (x 1, y 1)+ (x 2, y 2). So is a homomorphism.

Composition of group homomorphisms In fact, composition of group homomorphisms is again a group homomorphism. That is, if : G G’ and : G’ G’’ are both group homomorphisms then their composition ( ): G G’’, where ( )(g)= ( (g)) for g G. is also a homomorphism. Proof: Exercise 49.

Properties of Homomorphisms Definition Let be a mapping of a set X into a set Y, and let A X and B Y. • The image [A] of A in Y under is { (a) | a A}. • The set [X] is the range of . • The inverse image of -1 [B] of B in X is {x X | (x) B }.

Theorem Let be a homomorphism of a group G into a group G’. 1. If e is the identity element in G, then (e) is the identity element e’ in G’. 2. If a G, then (a-1)= (a)-1. 3. If H is a subgroup of G, then [H] is a subgroup of G’. 4. If K’ is a subgroup of G’, then -1 [K’] is a subgroup of G. Proof of the statement 3: Let H be a subgroup of G, and let (a) and (b) be any two elements in [H]. Then (a) (b)= (ab), so we see that (a) (b) [H]; thus [H] is closed under the operation of G’. The fact that e’= (e) and (a-1)= (a)-1 completes the proof that [H] is a subgroup of G’.

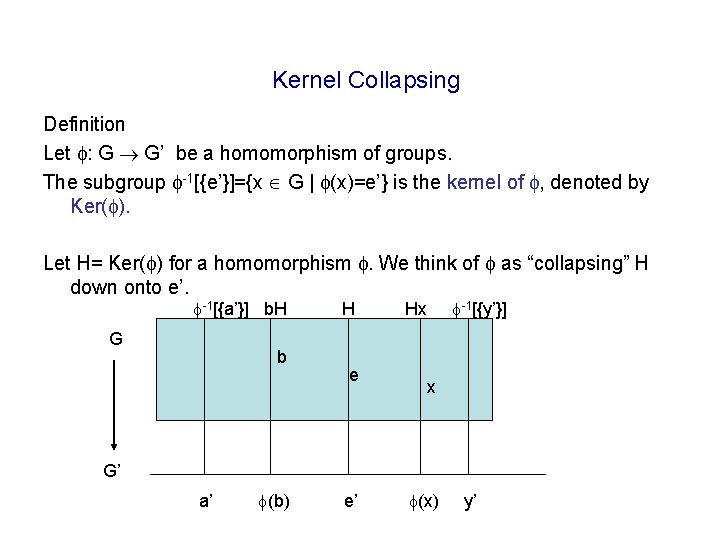
Kernel Collapsing Definition Let : G G’ be a homomorphism of groups. The subgroup -1[{e’}]={x G | (x)=e’} is the kernel of , denoted by Ker( ). Let H= Ker( ) for a homomorphism . We think of as “collapsing” H down onto e’. -1[{a’}] b. H G b H e -1[{y’}] Hx x G’ a’ (b) e’ (x) y’

Theorem Let : G G’ be a group homomorphism, and let H=Ker( ). Let a G. Then the set -1[{ (a)}]={ x G | (x)= (a)} is the left coset a. H of H, and is also the right coset Ha of H. Consequently, the two partitions of G into left cosets and into right cosets of H are the same. Corollary A group homomorphism : G G’ is a one-to-one map if and only if Ker( )={e}. Proof. Exercise.

Normal Subgroup Definition A subgroup H of a group G is normal if its left and right cosets coincide, that is if g. H = Hg for all g G. Note that all subgroups of abelian groups are normal. Corollary If : G G’ is a group homomorphism, then Ker( ) is a normal subgroup of G.