GRAFY PLANARNE To grafy ktre mona narysowa na

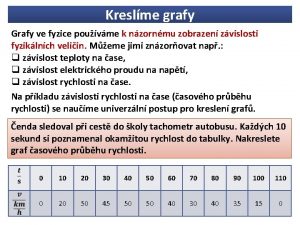
GRAFY PLANARNE • To grafy, które można narysować na płaszczyźnie tak, by krawędzie nie przecinały się (poza swoimi końcami). • Na przykład K_4, ale nie K_5. • Formalna definicja prowadzi przez grafy płaskie.

Grafy płaskie • G=(V, J) nazywamy grafem płaskim, gdy V jest skończonym podzbiorem punktów płaszczyzny euklidesowej, a J zbiorem (otwartych) krzywych Jordana o końcach w V i takich, że: 1) różne krzywe mają różne pary końców, 2) „wnętrza” krzywych nie zawierają punktów innych krzywych zbioru J ani żadnych punktów zbioru V.

Trzy interpretacje grafu płaskiego • Graf płaski G=(V, J) często utożsamiamy z grafem abstrakcyjnym G=(V, E), gdzie E={uv: u i v są końcami pewnej krzywej e z J}, • ale też ze zbiorem punktów na płaszczyźnie

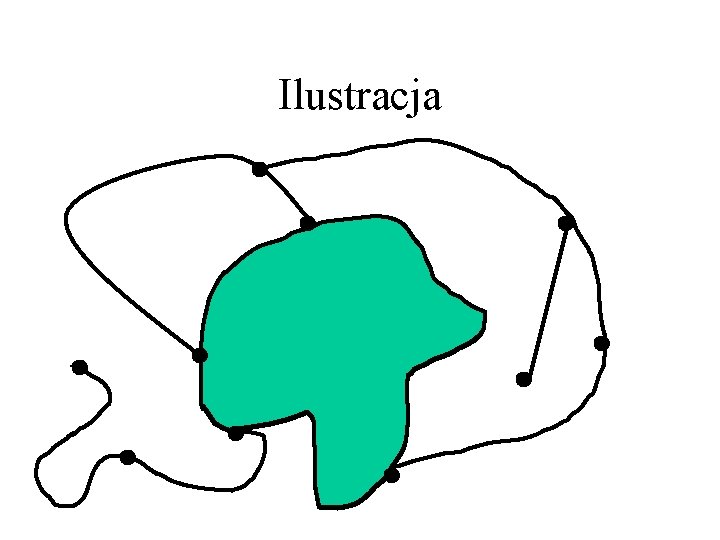
Ilustracja

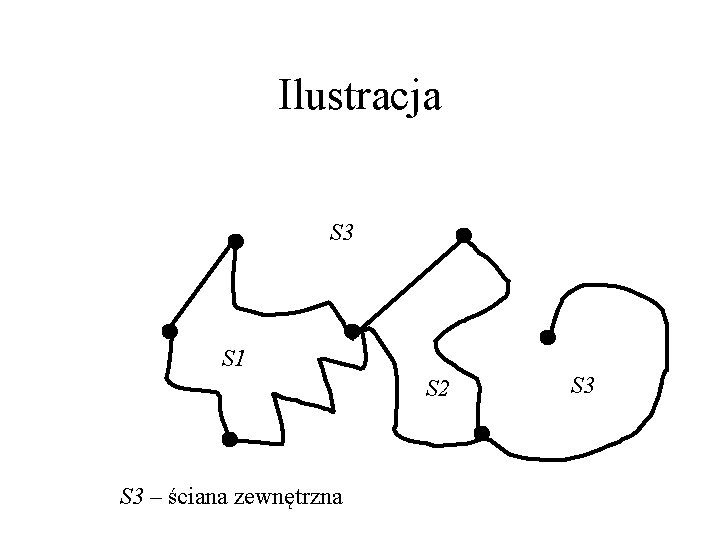
Ściany • jest otwartym podzbiorem płaszczyzny, • jego obszary spójne nazywamy ścianami grafu G, • dokładnie jedna ściana jest nieograniczona – nazywamy ją zewnętrzną, • brzeg ściany albo daną krawędź zawiera albo jest rozłączny z jej wnętrzem.

Ilustracja S 3 S 1 S 2 S 3 – ściana zewnętrzna S 3

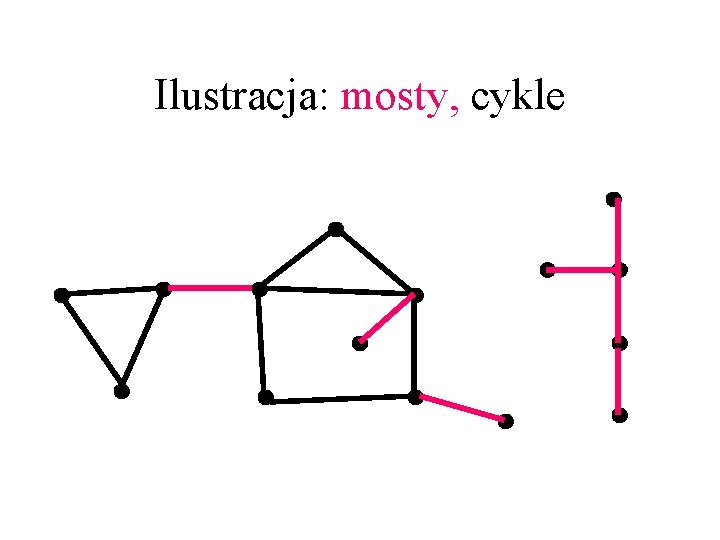
Mosty i nie-mosty Niech C będzie cyklem w grafie płaskim G. • Jeśli e należy do C, to e leży na brzegu dokładnie dwóch ścian i te ściany zawarte są w dwóch różnych ścianach grafu C. • Jeśli e jest mostem, to e leży na brzegu dokładnie jednej ściany. • Wniosek: płaski las ma tylko jedną ścianę.

Ilustracja: mosty, cykle

2 -spójne grafy płaskie Fakt: W 2 -spójnym grafie płaskim brzeg każdej ściany jest cyklem. Dowód: Indukcja z wykorzystaniem konstrukcyjnej charakterystyki grafów 2 -spójnych (ćw). � H P

Triangulacje • Graf płaski nazywamy maksymalnym, gdy żaden jego nadgraf właściwy o tym samym zbiorze wierzchołków nie jest płaski. • Graf płaski nazywamy triangulacją, gdy brzeg każdej ściany jest trójkątem. Fakt. Graf płaski o co najmniej 3 wierzchołkach jest maksymalny wgdy jest triangulacją.

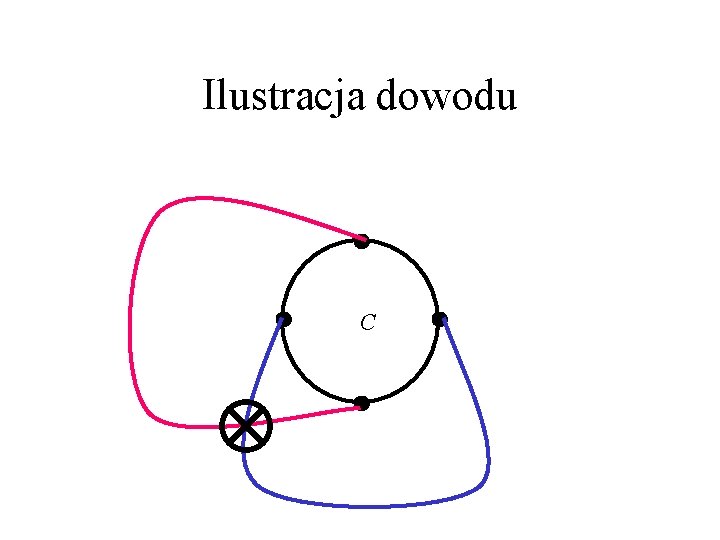
Dowód ß Jeśli każda ściana jest trójkątem, to nie można dodać krawędzi, która nie naruszałaby warunków 1) i 2) z def. płaskości. G musi być 2 -spójny, więc brzeg każdej ściany jest cyklem. Niech C będzie jednym z nich. Skoro G jest maksymalny, to V(C) jest kliką w G, której wszystkie krawędzie leżą na zewnątrz ściany C. Jest to jednak możliwe tylko, gdy |V(C)|<4 (patrz: rysunek). �

Ilustracja dowodu C

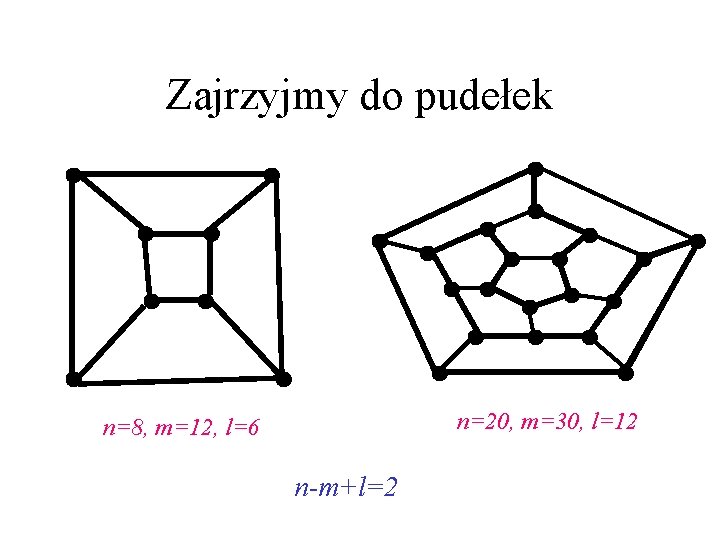
Zajrzyjmy do pudełek n=20, m=30, l=12 n=8, m=12, l=6 n-m+l=2

Wzór Eulera Tw. (Euler, 1752) W każdym spójnym grafie płaskim liczba wierzchołków n, liczba krawędzi m i liczba ścian l spełniają równość: n-m+l=2 Dowód: Indukcja względem m przy ustalonym n. Jeśli m=n-1, to G jest drzewem i l=1. Jeśli m>n-1, to G zawiera cykl. Usuńmy krawędź e z tego cyklu. Graf G-e ma 1 krawędź mniej i 1 ścianę mniej niż G. Stosujemy zał. ind. do G-e. �

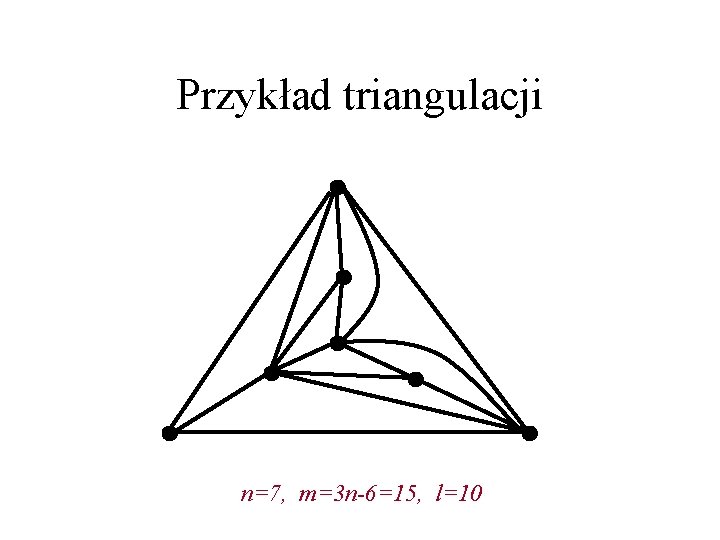
Liczba krawędzi grafu płaskiego Wniosek: Graf płaski o n wierzchołkach ma nie więcej niż 3 n-6 krawędzi, triangulacja ma ich dokładnie tyle. Dowód: Licząc krawędzie wokół każdej ściany triangulacji i sumując je, otrzymamy 2 m, ale jednocześnie 3 l. Stąd i ze wzoru Eulera pomnożonego przez 3, 3 n-3 m+2 m=6. �

Przykład triangulacji n=7, m=3 n-6=15, l=10

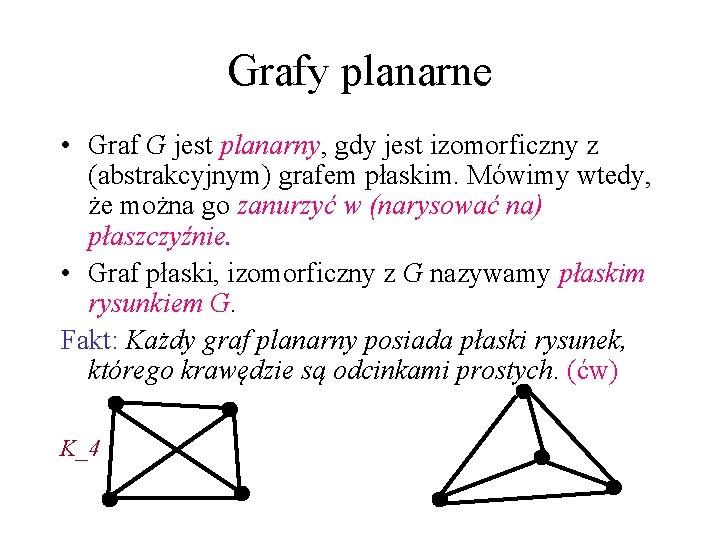
Grafy planarne • Graf G jest planarny, gdy jest izomorficzny z (abstrakcyjnym) grafem płaskim. Mówimy wtedy, że można go zanurzyć w (narysować na) płaszczyźnie. • Graf płaski, izomorficzny z G nazywamy płaskim rysunkiem G. Fakt: Każdy graf planarny posiada płaski rysunek, którego krawędzie są odcinkami prostych. (ćw) K_4

Równoważność topologiczna • Dwa płaskie rysunki tego samego grafu są topologicznie równoważne, gdy (multi)zbiory podgrafów będących brzegami ścian pokrywają się. • Przykład: Dwa top. równoważne rysunki K_4

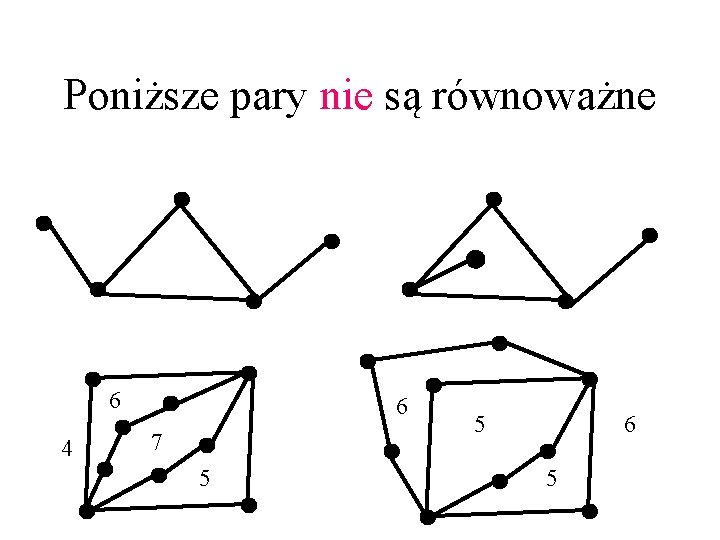
Poniższe pary nie są równoważne 6 4 6 7 5 5 6 5

3 -spójne grafy planarne Tw. (Whitney, 1932) Każde dwa płaskie rysunki 3 spójnego grafu planarnego są topologicznie równoważne. Lemat: Cykl C 3 -spójnego grafu płaskiego jest brzegiem ściany wgdy C jest cyklem indukowanym a V(C) nie rozspójnia G. Dowód Tw. : Z Lematu, każdy płaski rysunek 3 spójnego grafu planarnego ma te same cykle na brzegach ścian. � Dowód Lematu: Skoro V(C) nie rozspójnia G, to przynajmniej 1 ze ścian C nie zawiera punktów GC. Zatem C jest brzegiem ściany.

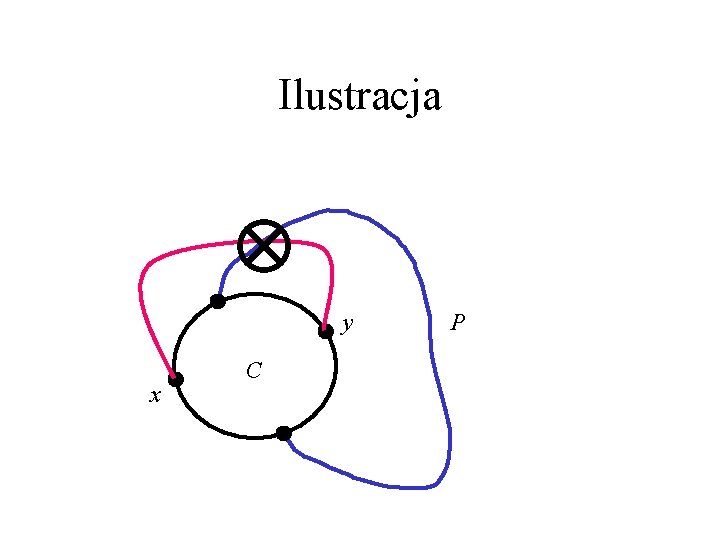
Dowód Lematu • Niech C będzie brzegiem ściany, a x, y dwoma (niesąsiednimi na C) wierzchołkami C. • Z 3 -spójności G, w G-{x, y} istnieje ścieżka P łącząca dwa ścieżki grafu C-{x, y}. • Gdyby istniała krawędź xy, to przecinałaby P (bo obie muszą biec przez zewnętrzną ścianę C) – sprzeczność! (bo G jest płaski). • Zatem C jest cyklem indukowanym.

Ilustracja y x C P

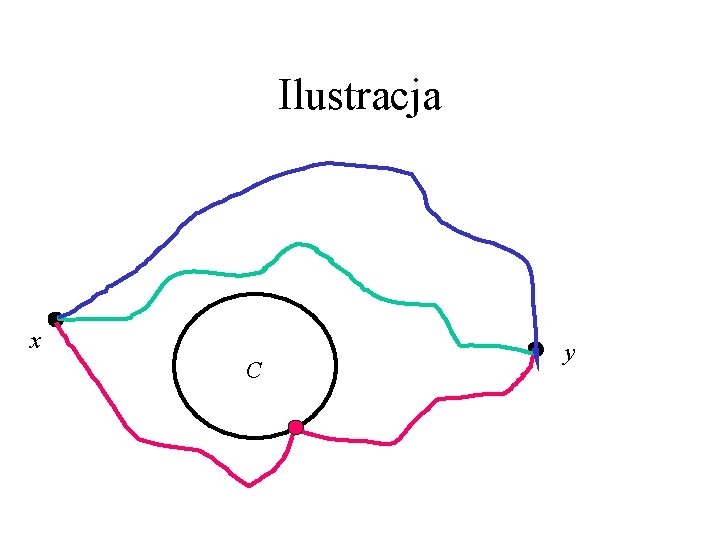
Dowód Lematu c. d. • Niech x, y należą do V(G)-V(C) • Z 3 -spójności G są między nimi co najmniej 3 niezależne ścieżki, które dzielą płaszczyznę na 3 rozłączne obszary. • C musi się zawierać w jednym z nich, a więc jedna ze ścieżek omija C. • Zatem zbiór V(C) nie rozspójnia x, y. �

Ilustracja x C y

Maksymalne grafy planarne • Graf planarny jest maksymalny, gdy żaden jego nadgraf właściwy o tym samym zbiorze wierzchołków nie jest planarny. • Płaski rysunek maksymalnego grafu planarnego jest triangulacją, i odwrotnie, każda triangulacja jest maksymalnym grafem planarnym. • Zatem, graf planarny o n>2 wierzchołkach jest maksymalny wgdy ma 3 n-6 krawędzi. • Dla n>3, triangulacje są 3 -spójne (dowód na ćw. )

Ani, ani • Wszystkie grafy na 4 wierzchołkach są planarne (bo K_4 jest planarny) • Wszystkie grafy na 5 wierzchołkach są planarne, oprócz K_5 (ćw. ) • Wszystkie grafy dwudzielne na 6 wierzchołkach są planarne, oprócz K_{3, 3} (ćw. ) • Ani K_5, ani K_{3, 3} nie jest planarny Dowód dla K_5: m=10>9=3 n-6 Dowód dla K_{3, 3}: na ćwiczeniach!

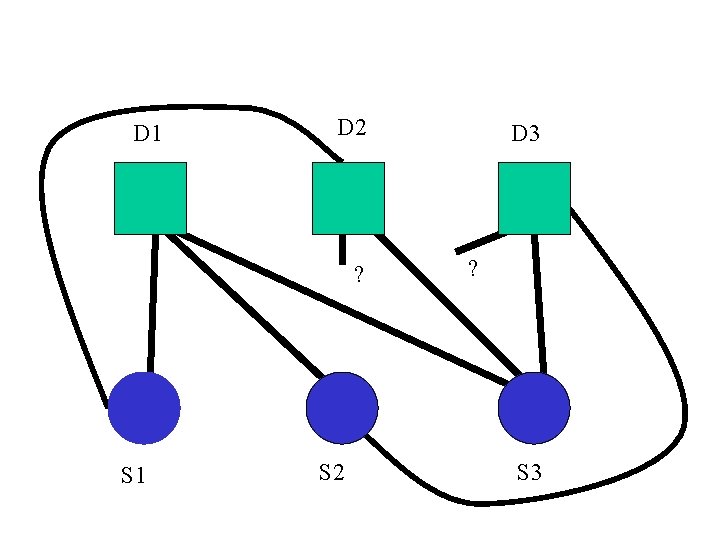
D 1 D 2 ? S 1 S 2 D 3 ? S 3

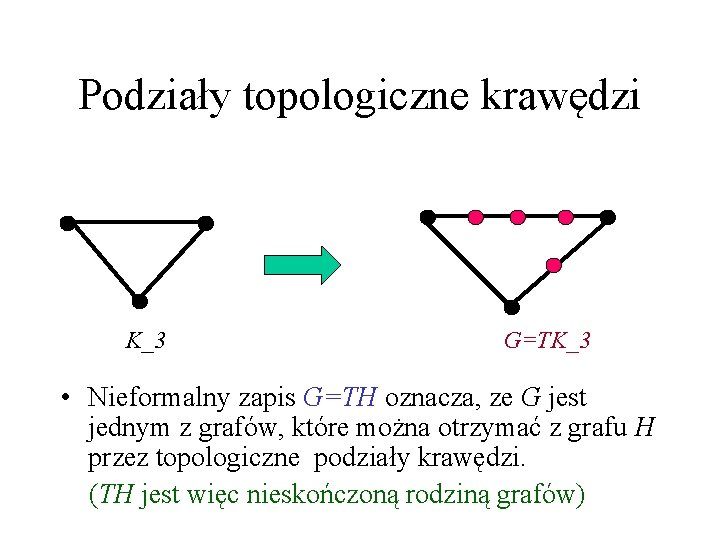
Podziały topologiczne krawędzi K_3 G=TK_3 • Nieformalny zapis G=TH oznacza, ze G jest jednym z grafów, które można otrzymać z grafu H przez topologiczne podziały krawędzi. (TH jest więc nieskończoną rodziną grafów)

Tw. Kuratowskiego • Ani TK_5, ani TK_{3, 3} nie jest planarny. • Żaden graf planarny nie zawiera ich. Tw. (Kuratowski 1930) Graf G jest planarny wgdy nie zawiera ani TK_5 ani TK_{3, 3}. (bez dowodu. )