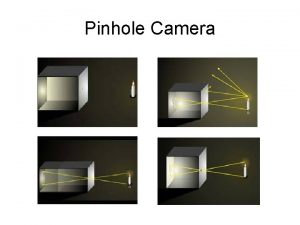
Geometry of Images n n n Pinhole camera

Geometry of Images n n n Pinhole camera, projection A taste of projective geometry Two view geometry: q q q n n Homography Epipolar geometry, the essential matrix Camera calibration, the fundamental matrix Stereo vision: 3 D shape reconstruction from two views Factorization: reconstruction from many views

Geometry of Images

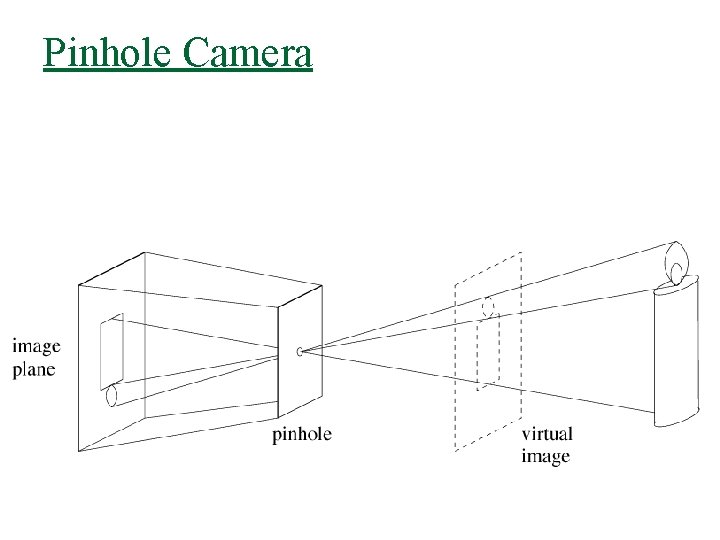
Cameras n n n Camera obscura dates from 15 th century First photograph on record shown in the book 1822 Basic abstraction is the pinhole camera Current cameras contain a lens and a recording device (film, CCD) The human eye functions very much like a camera

Camera Obscura "Reinerus Gemma-Frisius, observed an eclipse of the sun at Louvain on January 24, 1544, and later he used this illustration of the event in his book De Radio Astronomica et Geometrica, 1545. It is thought to be the first published illustration of a camera obscura. . . " Hammond, John H. , The Camera Obscura, A Chronicle

Why Not Use Pinhole Camera n If pinhole is too big many directions are averaged, blurring the image n Pinhole too small diffraction effects blur the image n Generally, pinhole cameras are dark, because a very small set of rays from a particular point hits the screen.

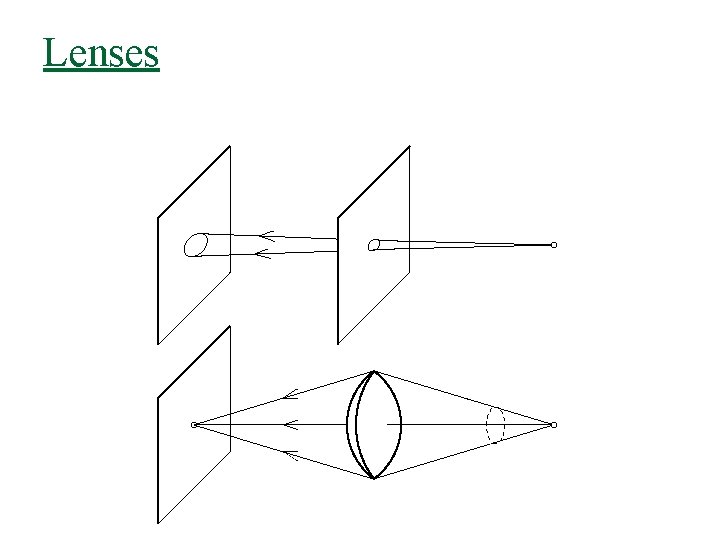
Lenses

Lenses n n n Lenses collect light from a large hole and direct it to a single point Overcome the darkness of pinhole cameras But there is a price q q n Focus Radial distortions Chromatic abberations … Pinhole is useful as a model

Pinhole Camera

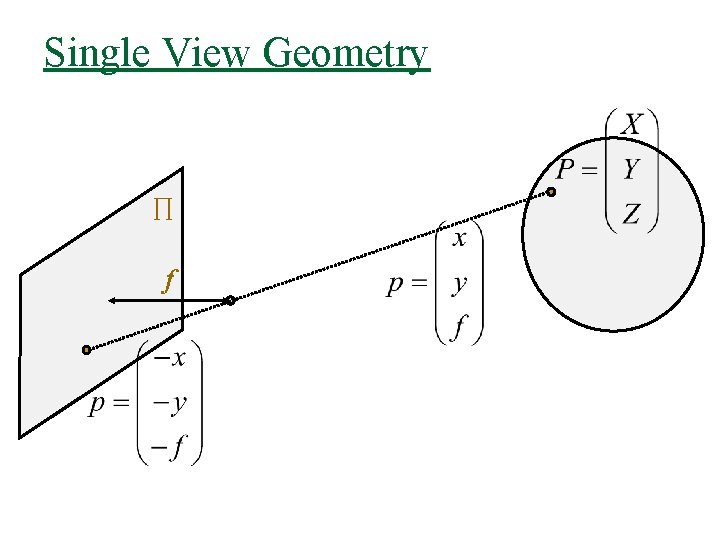
Single View Geometry ∏ f

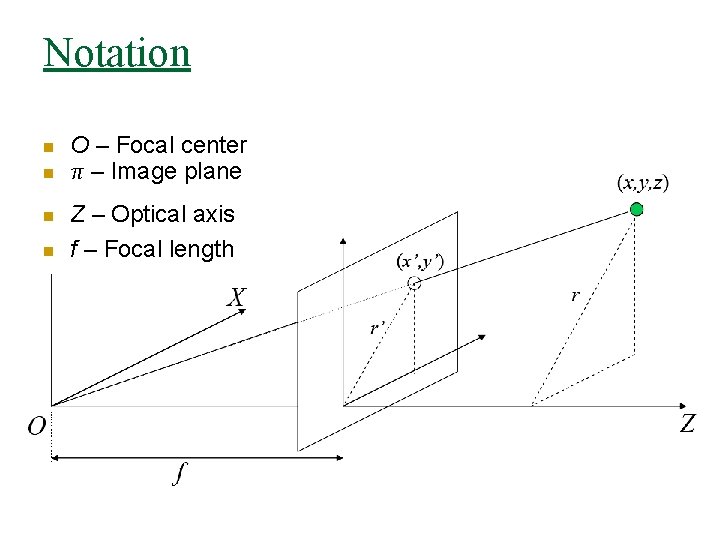
Notation n n O – Focal center π – Image plane Z – Optical axis f – Focal length

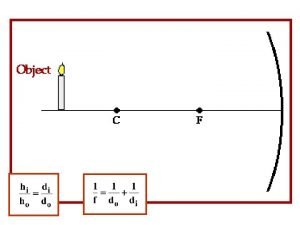
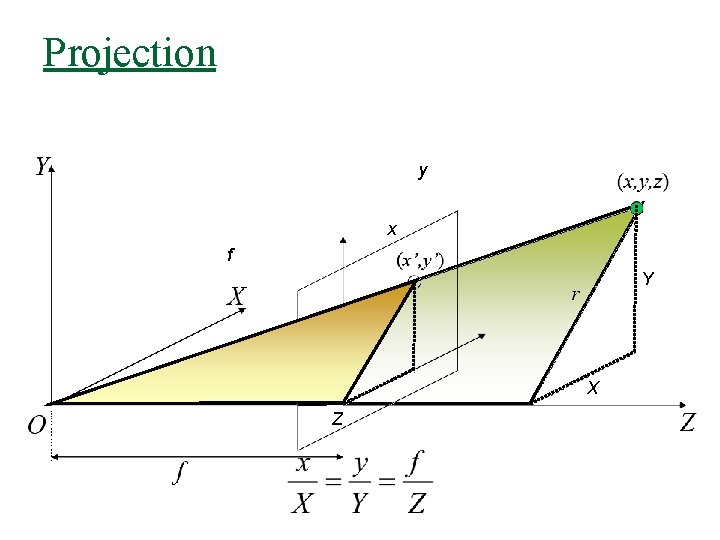
Projection y x f Y X Z

Perspective Projection Homogeneous Coordinates

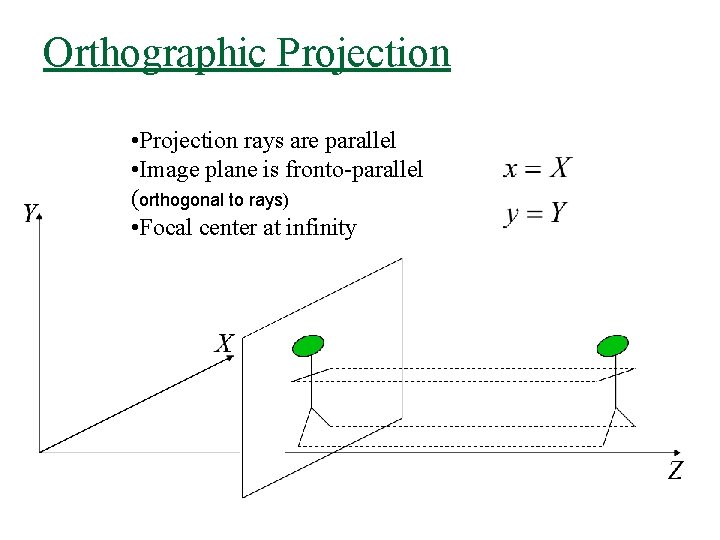
Orthographic Projection • Projection rays are parallel • Image plane is fronto-parallel (orthogonal to rays) • Focal center at infinity

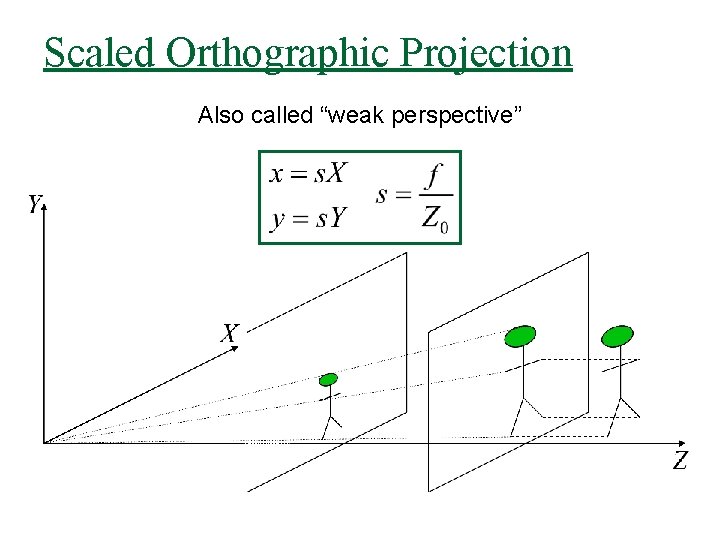
Scaled Orthographic Projection Also called “weak perspective”

Pros and Cons of Projection Models n Weak perspective has simpler math. q q n Pinhole perspective much more accurate for scenes. q n Accurate when object is small and distant. Most useful for recognition of objects. Used in structure from motion. When accuracy really matters, we must model the real camera q Use perspective projection with other calibration parameters (e. g. , radial lens distortion)

World Cup 66: England-Germany

World Cup 66: Second View

World Cup 66: England-Germany Conclusion: no goal (missing 3 inches) (Reid and Zisserman, “Goal-directed video metrology”)

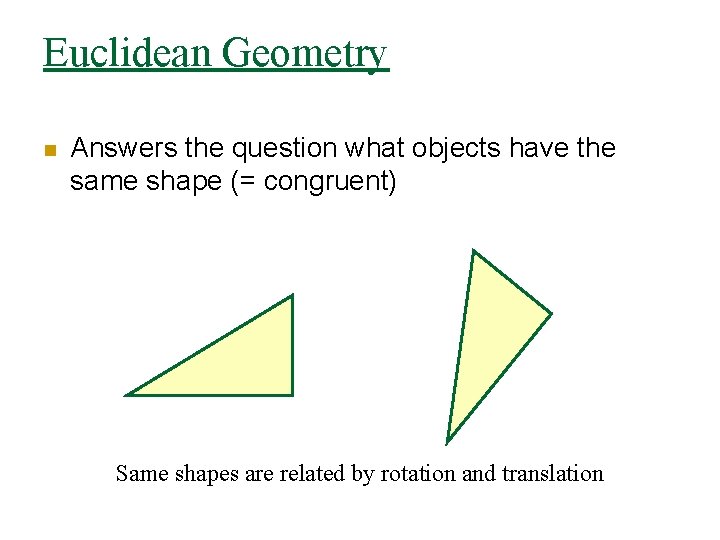
Euclidean Geometry n Answers the question what objects have the same shape (= congruent) Same shapes are related by rotation and translation

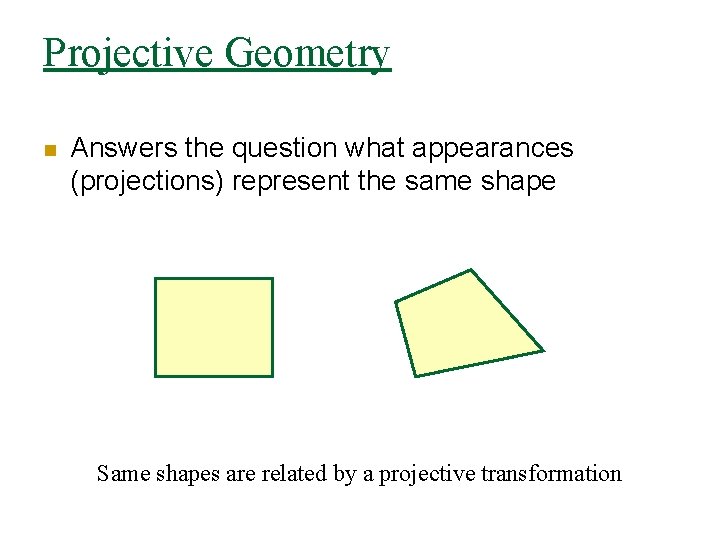
Projective Geometry n Answers the question what appearances (projections) represent the same shape Same shapes are related by a projective transformation

Perspective Distortion Parallel lines meet at the horizon (“vanishing line”) Where do parallel lines meet?

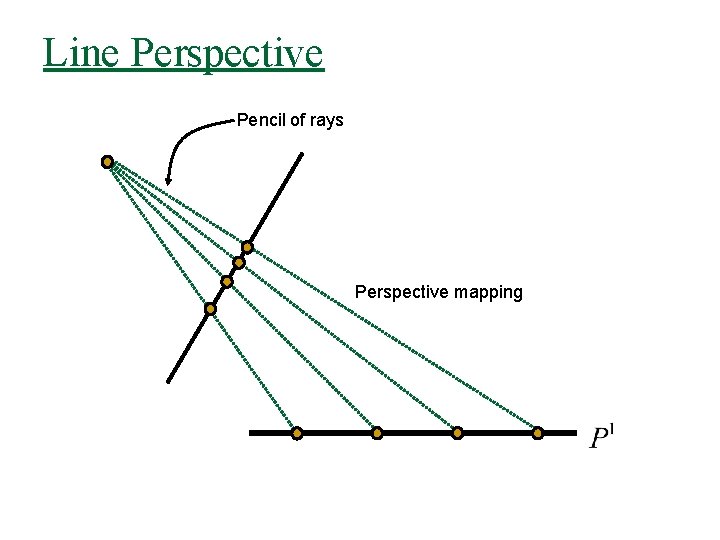
Line Perspective Pencil of rays Perspective mapping

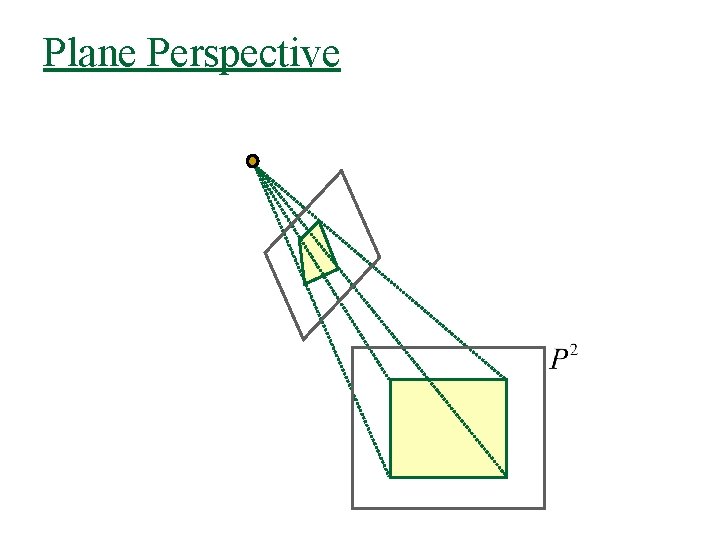
Plane Perspective

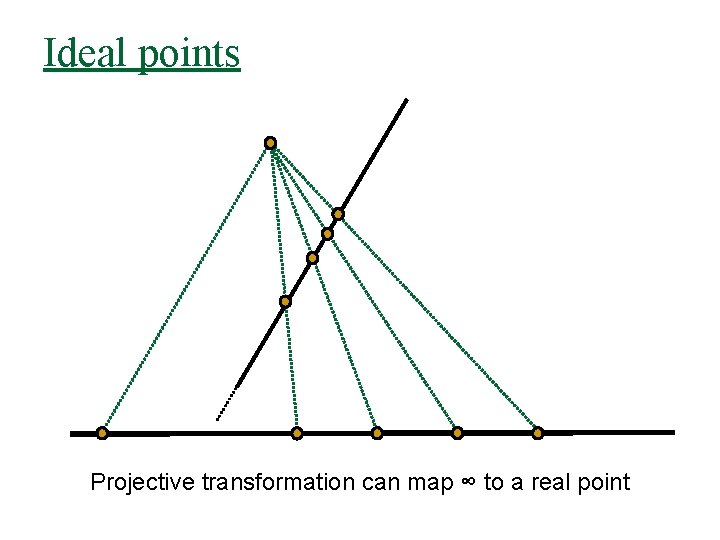
Ideal points Projective transformation can map ∞ to a real point

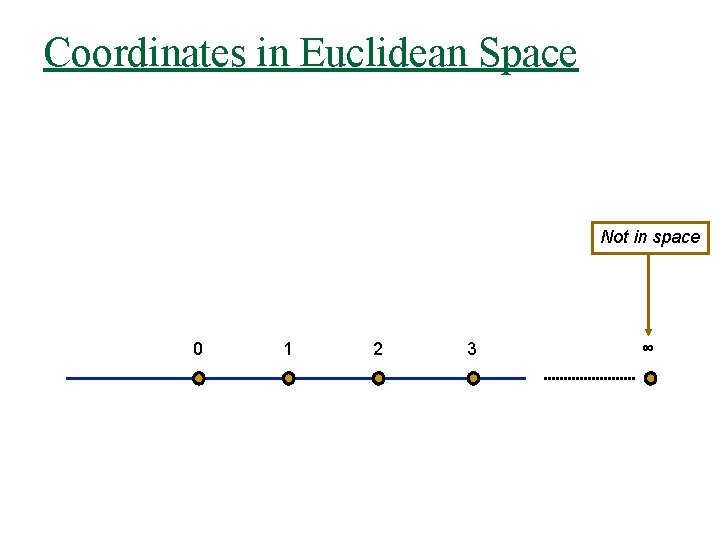
Coordinates in Euclidean Space Not in space 0 1 2 3 ∞

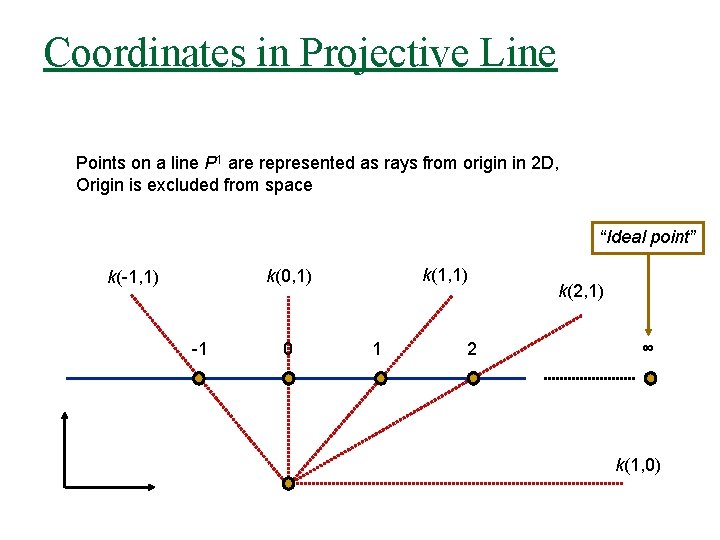
Coordinates in Projective Line Points on a line P 1 are represented as rays from origin in 2 D, Origin is excluded from space “Ideal point” k(1, 1) k(0, 1) k(-1, 1) -1 0 1 2 k(2, 1) ∞ k(1, 0)

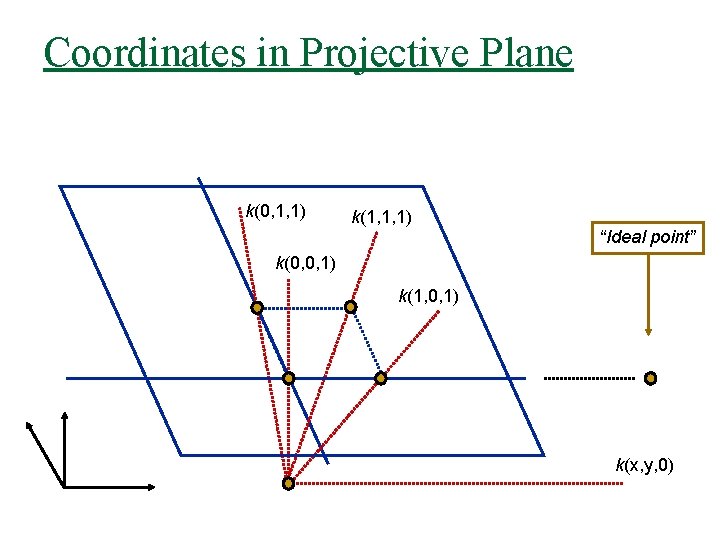
Coordinates in Projective Plane k(0, 1, 1) k(1, 1, 1) “Ideal point” k(0, 0, 1) k(1, 0, 1) k(x, y, 0)

2 D Projective Geometry: Basics n A point: n A line: we denote a line with a 3 -vector n Points and lines are dual: p is on l if n Intersection of two lines: n A line through two points:

Cross Product Every entry is a determinant of the two other entries Area of parallelogram bounded by u and v

Ideal points Q: How many ideal points are there in P 2? A: 1 degree of freedom family – the line at infinity

Projective Transformation (Homography) n n Any finite sequence of perspectivities is a projective transformation Projective transformations map lines to lines Represented by an invertible 3 x 3 linear transformation (up to scale), denote by H , or Given homography H, how does it operate on lines?

Euclidean Transformations (Isometries) Rotation: Translation:

Hierarchy of Transformations n Isometry (Euclidean), n Similarity, n Affine, n Projective, general linear

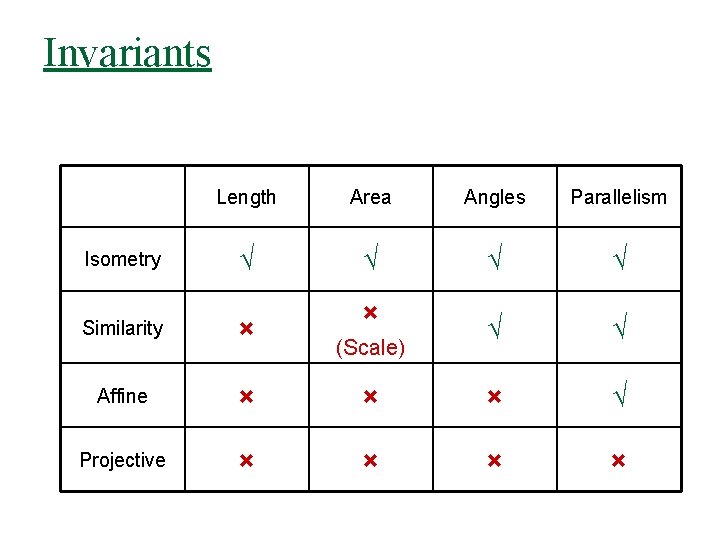
Invariants Isometry Length Area Angles Parallelism √ √ √ × Similarity × Affine × × × √ Projective × × (Scale)

Perspective Projection Note: P and p are related by a scale factor, but it is a different factor for each point (depends on Z)

Two View Geometry n n When a camera changes position and orientation, the scene moves rigidly relative to the camera In two cases this results in homography: Camera rotates around its focal point q The scene is planar In this case the mapping from one image to the second is one to one and depth cannot be recovered q n In the general case the induced motion is more complex and is captured by what is termed “epipolar geometry”

Camera Rotation (R is 3 x 3 non-singular)

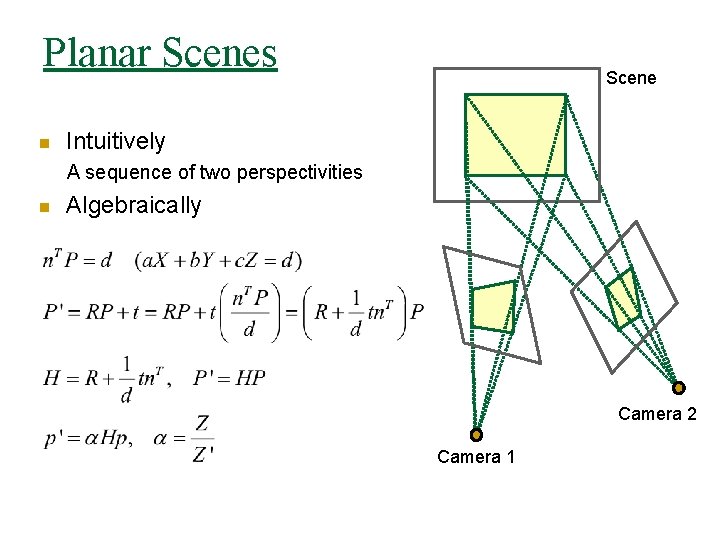
Planar Scenes n Scene Intuitively A sequence of two perspectivities n Algebraically Camera 2 Camera 1

Two Views Related by Homography Two images are related by homography: n n n One to one mapping from p to p’ H contains 8 degrees of freedom Given correspondences, each point determines 2 equations 4 points are required to recover H Depth cannot be recovered

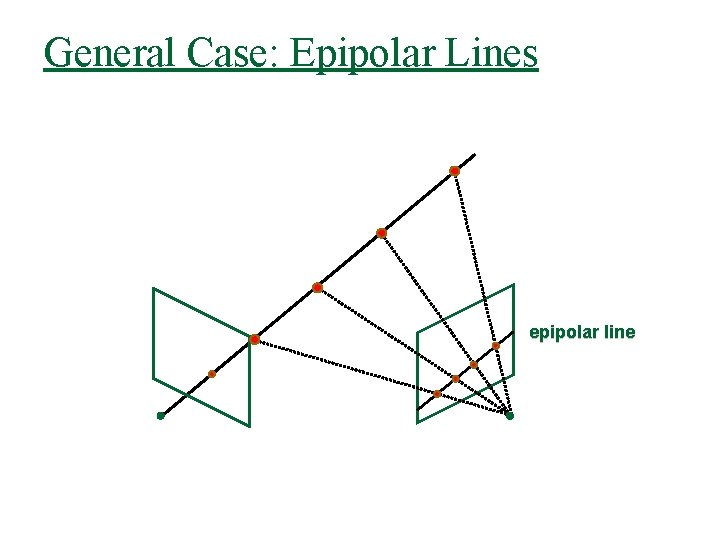
General Case: Epipolar Lines epipolar line

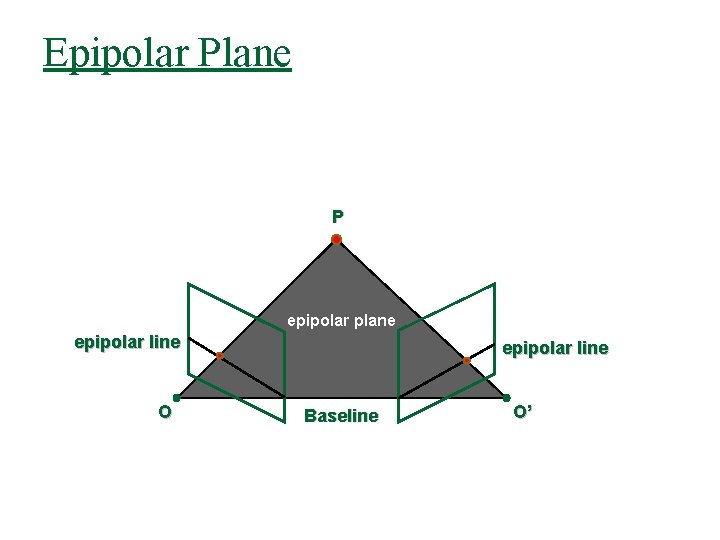
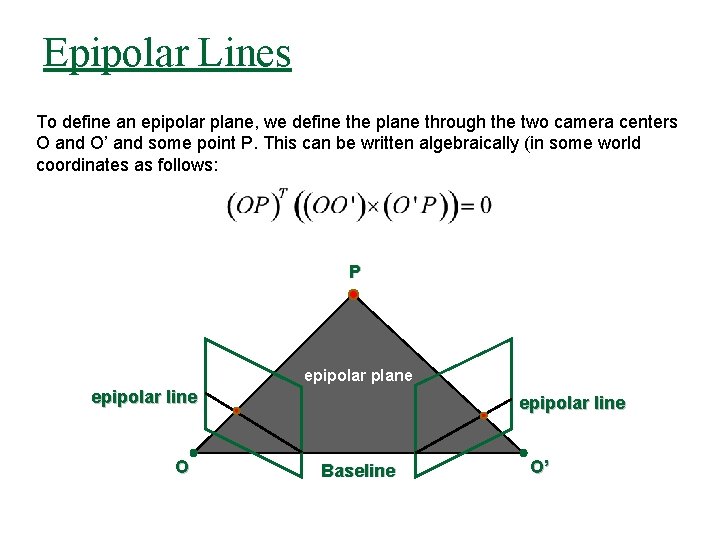
Epipolar Plane P epipolar plane epipolar line O epipolar line Baseline O’

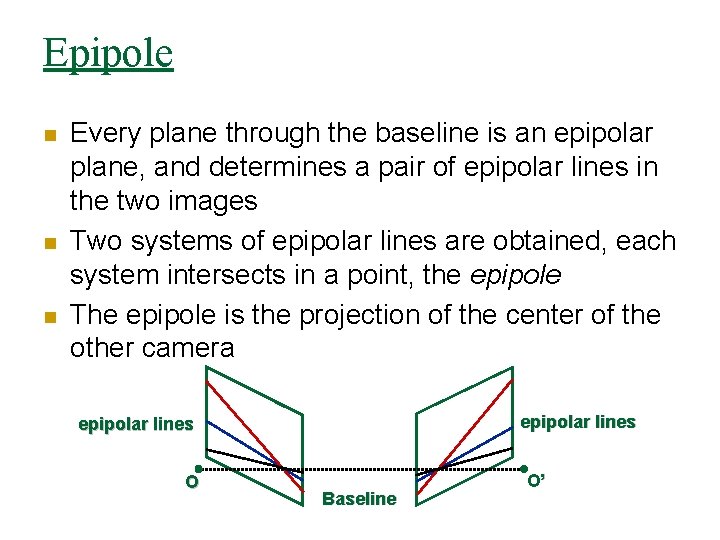
Epipole n n n Every plane through the baseline is an epipolar plane, and determines a pair of epipolar lines in the two images Two systems of epipolar lines are obtained, each system intersects in a point, the epipole The epipole is the projection of the center of the other camera epipolar plane epipolar lines O Baseline epipolar lines O’

Epipolar Lines To define an epipolar plane, we define the plane through the two camera centers O and O’ and some point P. This can be written algebraically (in some world coordinates as follows: P epipolar plane epipolar line O epipolar line Baseline O’

Epipolar Lines n Set world coordinates around the first camera n What to do with O’P? Every rotation changes the observed coordinate in the second image We need to de-rotate to make the second image plane parallel to the first n n Replacing by image points

Essential Matrix n Denote this by: n Then n Define n E is called the “essential matrix” , then

Essential Matrix n n E is rank 2. Its (right and left) null spaces are the two epipoles is linear and homogeneous in E, E can be recovered up to scale using 8 points The additional constraint det. E=0 reduces the needed points to 7 In fact, there are only 5 degrees of freedom in E, q q 3 for rotation 2 for translation (up to scale), determined by epipole

Internal Calibration n Camera parameters may be unknown: n (cx, cy) camera center, (ax, ay) pixel dimensions, b skew n Radial distortions are not accounted for

Fundamental Matrix n n F, the fundamental matrix, too is rank 2 F has 7 d. o. f. (9 entries, homogeneous, and det. F=0)

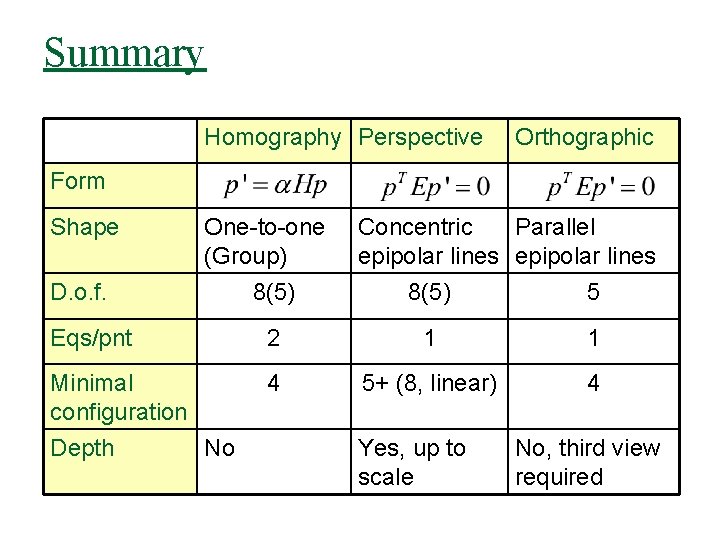
Summary Homography Perspective Orthographic Form Shape One-to-one (Group) D. o. f. Concentric Parallel epipolar lines 8(5) 5 Eqs/pnt 2 1 1 Minimal configuration Depth No 4 5+ (8, linear) 4 Yes, up to scale No, third view required