Geometria de Posio Conceitos primitivos Prof Mrcio Conceitos

Geometria de Posição Conceitos primitivos Prof. Márcio

Conceitos primitivos • A partir do mundo real, matemáticos da antiguidade, como Euclides (séc. III a. C. ) estabeleceram entes com os quais construíram a geometria. Três desses entes destacam-se por serem conhecidos intuitivamente. São eles: o ponto, a reta e o plano.

O Ponto • Olhando-se a noite para um céu estrelado vêem-se as estrelas, que, intuitivamente, podem ser consideradas pontos. Em geometria, o ponto, elemento concebido sem dimensão, massa nem volume, é uma noção primitiva.

A Reta • Suponha agora que fosse possível esticar, indefinidamente e nos dois sentidos, um fio de elástico. Em nossa imaginação, e apenas nela, visualizaríamos o que chamamos de reta. Em geometria, o conceito de reta – concebido intuitivamente – também é uma noção primitiva.

O Plano • Considere o tampo liso de uma mesa, sem nenhum tipo de fresta ou ondulação. Esse tampo possibilitaria a visualização concreta de um plano Entretanto, o conceito geométrico de plano implica que, por intuição, ele seja entendido ilimitadamente em todas as direções. Plano é uma noção primitiva.

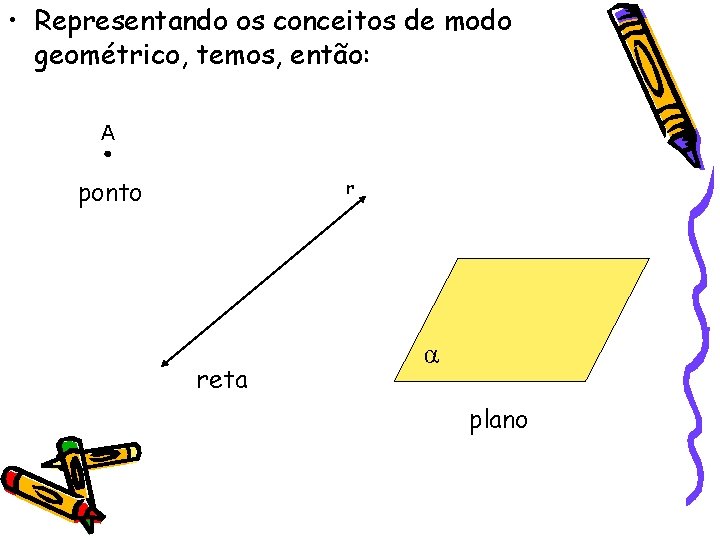
• Representando os conceitos de modo geométrico, temos, então: A ponto r reta α plano

• A proposição usada por Hilbert (1862 – 1943), e normalmente adotada por nós, é a seguinte: • Os pontos são indicados por letras maiúsculas (A, B, C etc. ). • As retas são indicadas por letras minúsculas (r, s, t etc. ). • Os planos são indicados por letras gregas (α, β, γ etc. ).

Posições primitivas, postulados ou axiomas. Postulados da existência P 1 – Existem infinitos pontos P 2 – Em uma reta e fora dela existem infinitos pontos A r C B F E D P 3 – Em um plano e fora dele existem infinitos pontos D A E α C B F

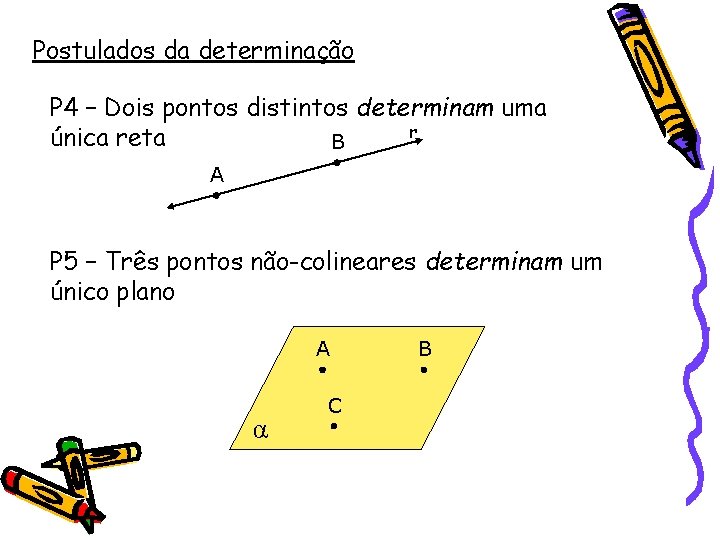
Postulados da determinação P 4 – Dois pontos distintos determinam uma r única reta B A P 5 – Três pontos não-colineares determinam um único plano A α C B

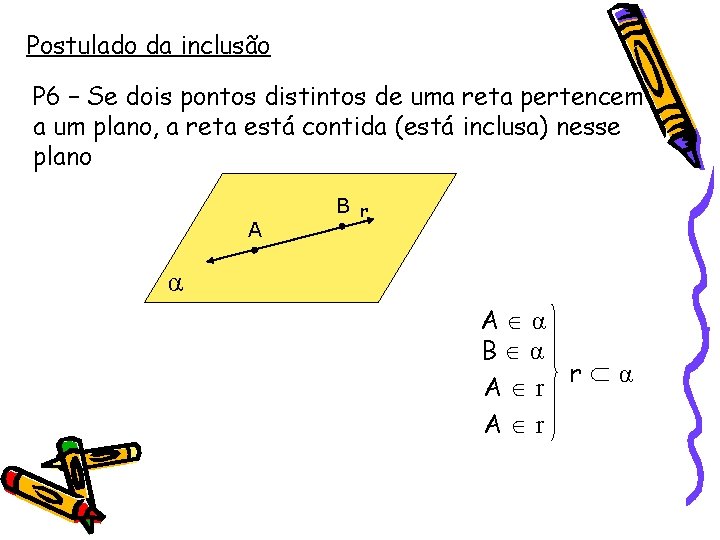
Postulado da inclusão P 6 – Se dois pontos distintos de uma reta pertencem a um plano, a reta está contida (está inclusa) nesse plano A B r A α B α r A r ∩ α α

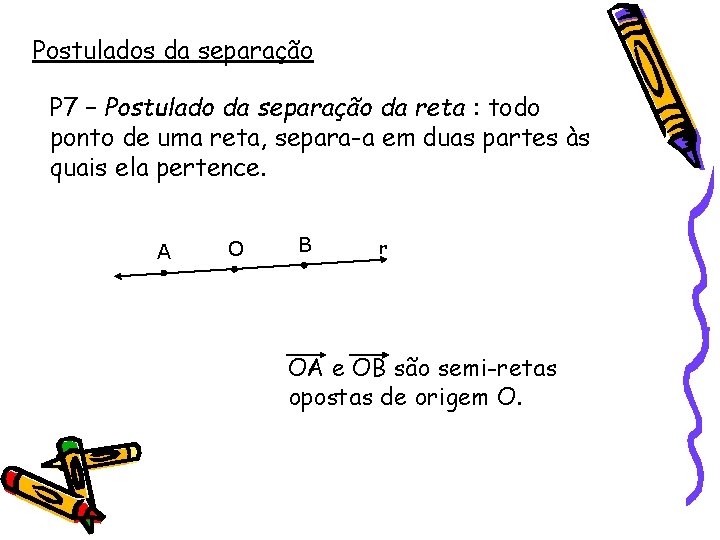
Postulados da separação P 7 – Postulado da separação da reta : todo ponto de uma reta, separa-a em duas partes às quais ela pertence. A O B r OA e OB são semi-retas opostas de origem O.

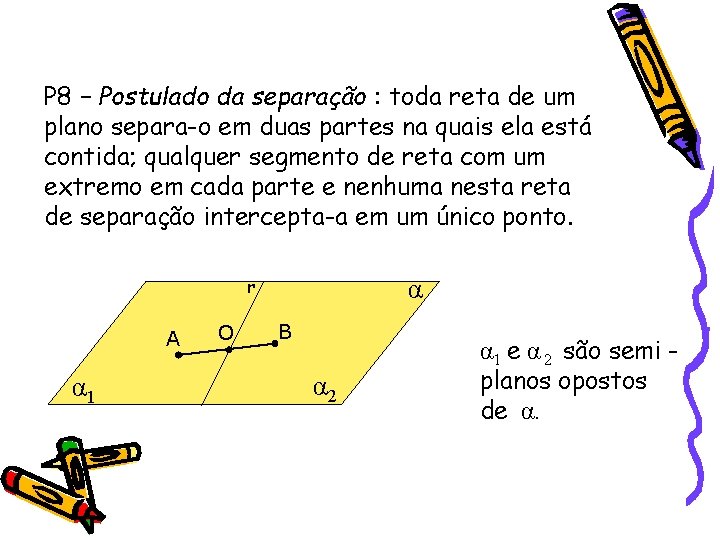
P 8 – Postulado da separação : toda reta de um plano separa-o em duas partes na quais ela está contida; qualquer segmento de reta com um extremo em cada parte e nenhuma nesta reta de separação intercepta-a em um único ponto. α r A α 1 O B α 2 α 1 e α 2 são semi planos opostos de α.

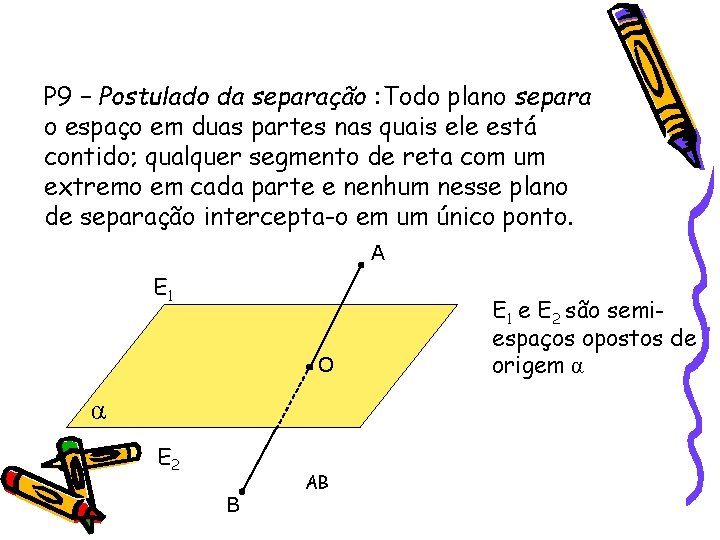
P 9 – Postulado da separação : Todo plano separa o espaço em duas partes nas quais ele está contido; qualquer segmento de reta com um extremo em cada parte e nenhum nesse plano de separação intercepta-o em um único ponto. A E 1 O α E 2 B AB E 1 e E 2 são semiespaços opostos de origem α

Exercício 1. Prove que em um plano existem infinitas retas. 2. Classifique como verdadeira ou falsa cada uma das seguintes sentenças, justificando cada resposta. a. b. c. Três pontos distintos determinam um único plano. Os vértices de um triangulo são coplanares. Se três pontos são coplanares, então eles são colineares.

Posições relativas entre duas retas Consideremos duas retas, r e s, do espaço. Elas podem ser: • Coincidentes: se todos os pontos de uma são pontos da outra. r s Indicamos: r = s

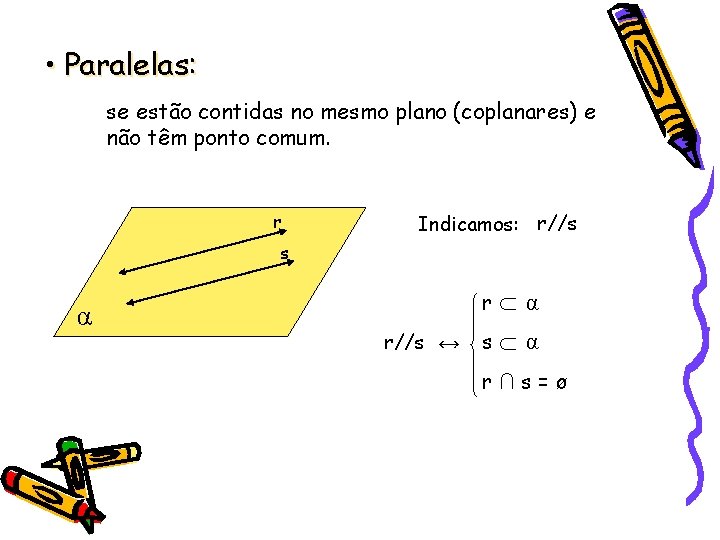
• Paralelas: se estão contidas no mesmo plano (coplanares) e não têm ponto comum. r Indicamos: r//s ↔ s ∩ α r α ∩ s α r∩s=ø

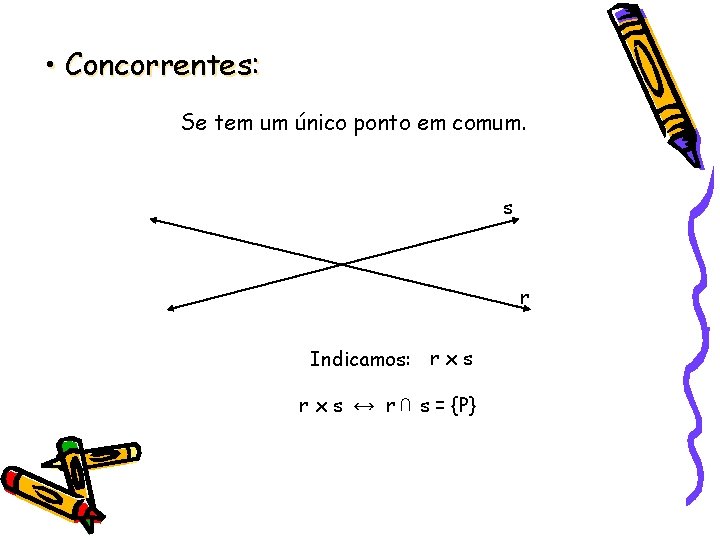
• Concorrentes: Se tem um único ponto em comum. s r Indicamos: r x s ↔ r ∩ s = {P}

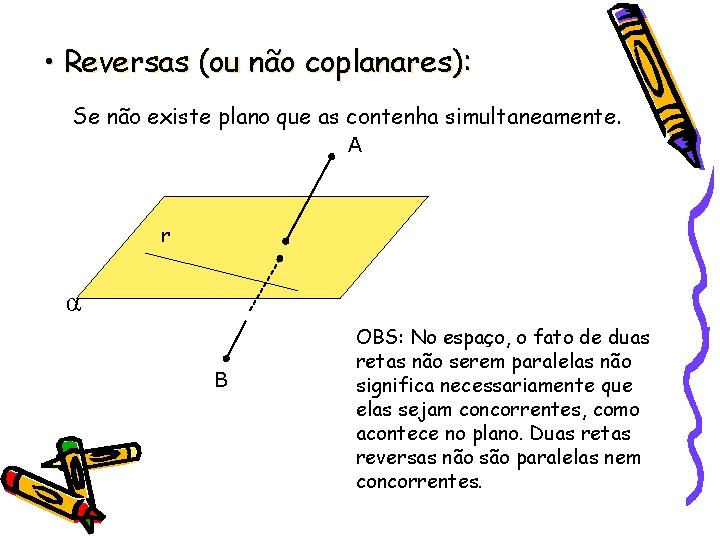
• Reversas (ou não coplanares): Se não existe plano que as contenha simultaneamente. A r α B OBS: No espaço, o fato de duas retas não serem paralelas não significa necessariamente que elas sejam concorrentes, como acontece no plano. Duas retas reversas não são paralelas nem concorrentes.

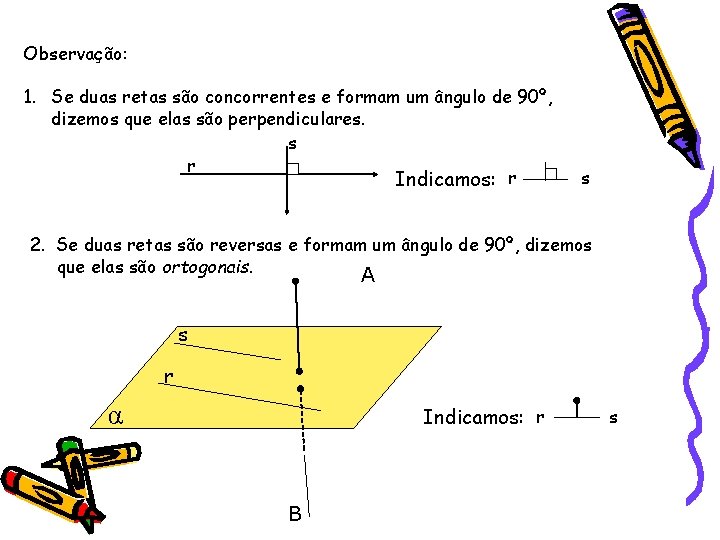
Observação: 1. Se duas retas são concorrentes e formam um ângulo de 90º, dizemos que elas são perpendiculares. s r Indicamos: r s 2. Se duas retas são reversas e formam um ângulo de 90º, dizemos que elas são ortogonais. A s r α Indicamos: r B s

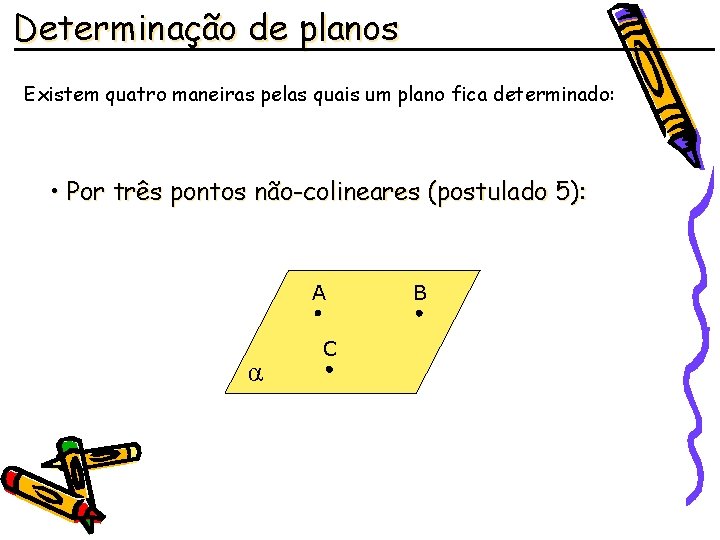
Determinação de planos Existem quatro maneiras pelas quais um plano fica determinado: • Por três pontos não-colineares (postulado 5): A α C B

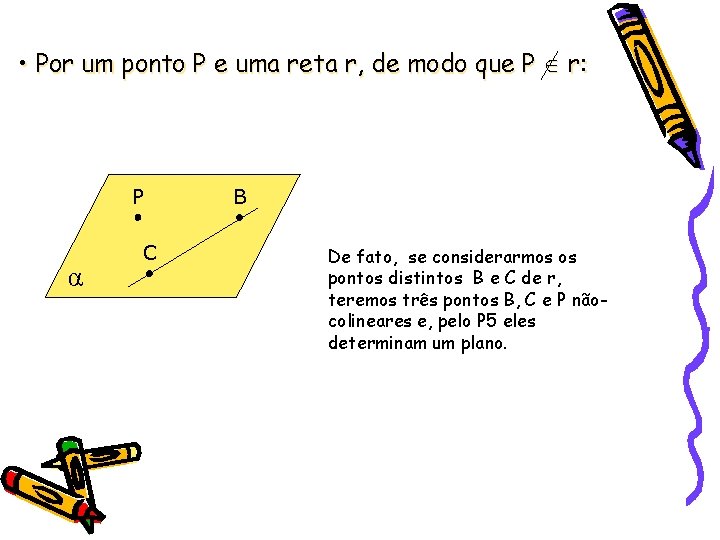
• Por um ponto P e uma reta r, de modo que P r: P α C B De fato, se considerarmos os pontos distintos B e C de r, teremos três pontos B, C e P nãocolineares e, pelo P 5 eles determinam um plano.

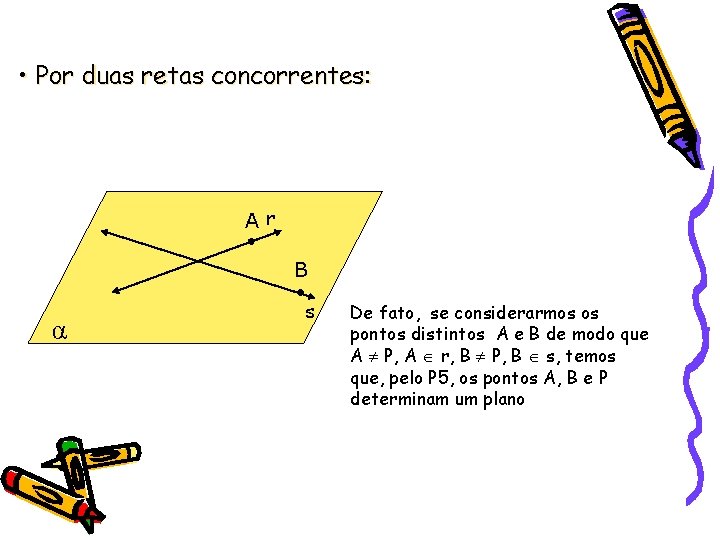
• Por duas retas concorrentes: Ar B α s De fato, se considerarmos os pontos distintos A e B de modo que A P, A r, B P, B s, temos que, pelo P 5, os pontos A, B e P determinam um plano

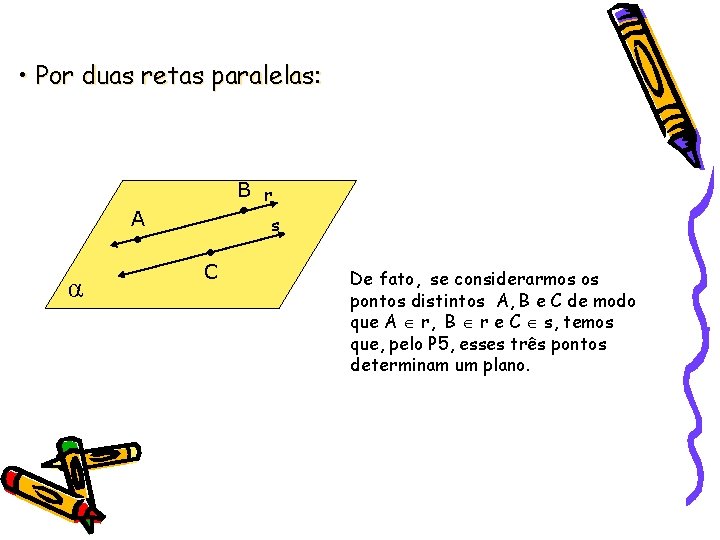
• Por duas retas paralelas: B r A α s C De fato, se considerarmos os pontos distintos A, B e C de modo que A r, B r e C s, temos que, pelo P 5, esses três pontos determinam um plano.

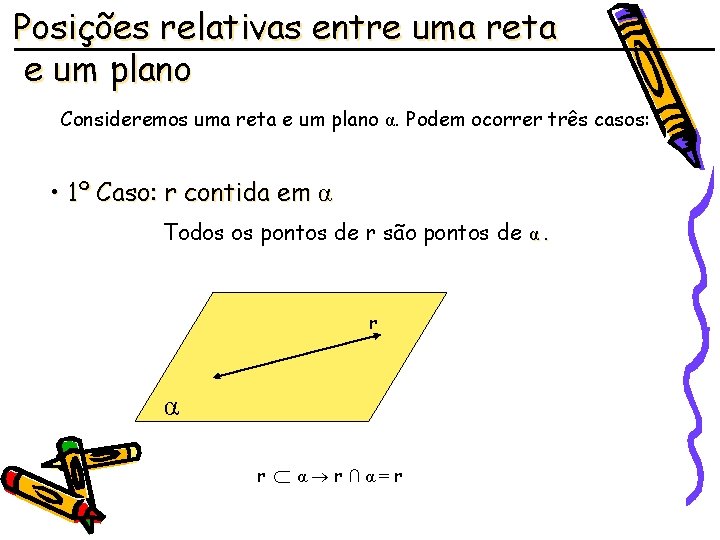
Posições relativas entre uma reta e um plano Consideremos uma reta e um plano α. Podem ocorrer três casos: • 1º Caso: r contida em α Todos os pontos de r são pontos de α. r r ∩ α α r∩α=r

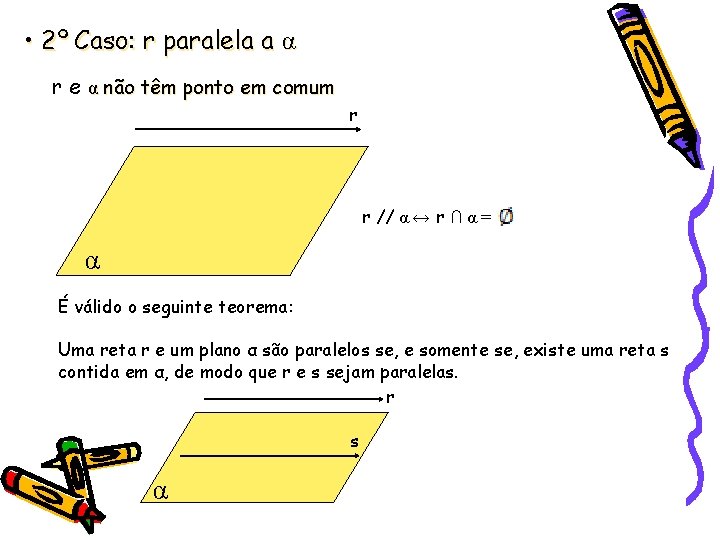
• 2º Caso: r paralela a α r e α não têm ponto em comum r r // α ↔ r ∩ α = α É válido o seguinte teorema: Uma reta r e um plano α são paralelos se, e somente se, existe uma reta s contida em α, de modo que r e s sejam paralelas. r s α

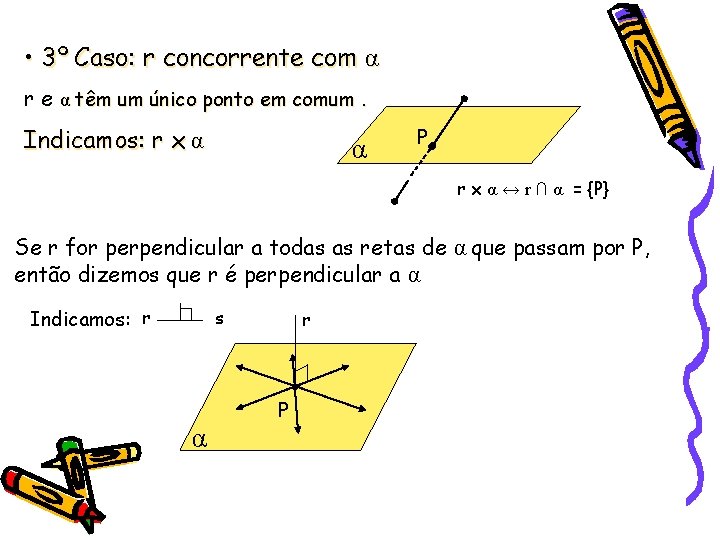
• 3º Caso: r concorrente com α r e α têm um único ponto em comum. Indicamos: r x α α P r x α ↔ r ∩ α = {P} Se r for perpendicular a todas as retas de α que passam por P, então dizemos que r é perpendicular a α Indicamos: r s r P α

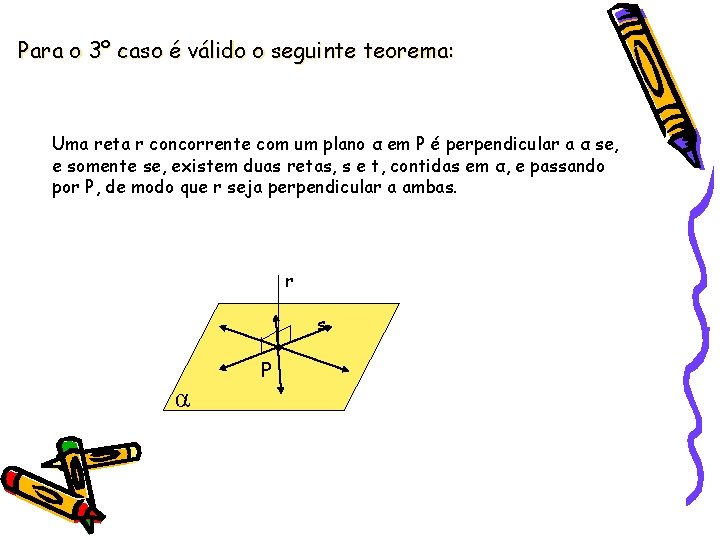
Para o 3º caso é válido o seguinte teorema: Uma reta r concorrente com um plano α em P é perpendicular a α se, e somente se, existem duas retas, s e t, contidas em α, e passando por P, de modo que r seja perpendicular a ambas. r s P α