Generacin de Nmeros SeudoAleatorios En la prctica ninguna






























- Slides: 40

Generación de Números Seudo-Aleatorios En la práctica ninguna función produce datos aleatorios verdaderos. Las funciones producen números pseudo-aleatorios. 1

Generación de Números Seudo-Aleatorios Un elemento importante en simulación es tener rutinas que generen variables aleatorias con distribuciones específicas: uniforme, normal, etc. Para ello la base es generar una secuencia de números aleatorios distribuidos uniformemente entre 0 y 1. 2 Y para ello la clave es generar números enteros aleatorios y uniformemente distribuidos en un cierto intervalo de una manera eficiente.

Técnicas para generar números aleatorios La mayoría de los métodos (generadores) comienzan con un número inicial (semilla), a este número se le aplica un determinado procedimiento y así se encuentra el primer número random. Usando este número como entrada, el procedimiento es repetido para lograr un próximo número random. 3

Técnicas para generar números aleatorios Método Del Cuadrado Medio: comienza con un número inicial (semilla). Este número es elevado al cuadrado. Se escogen los dígitos del medio de este nuevo número (según los dígitos que se deseen) y se colocan después del punto decimal. Este número conforma el primer número random. 4 Ejemplo: X 0 = 5497 X 02 = (5497)2 = 30, 217, 009 ===> X 1 = 2170 R 1 = 0. 2170 X 12 = (2170)2 = 04, 708, 900 ===> X 2 = 7089 R 2 = 0. 7089 X 22 = (7089)2 = 50, 253, 921 ===> X 3 = 2539

Operación mod l k mod m es el residuo de hacer la división de k entre m Sea x un entero grande 45 mod 12 = (5+55 x) mod 5 = (5+55 x) mod 11 = 5

Método de la Congruencia Lineal 6

7 El número aleatorio se encuentra de la siguiente manera: R = x / m

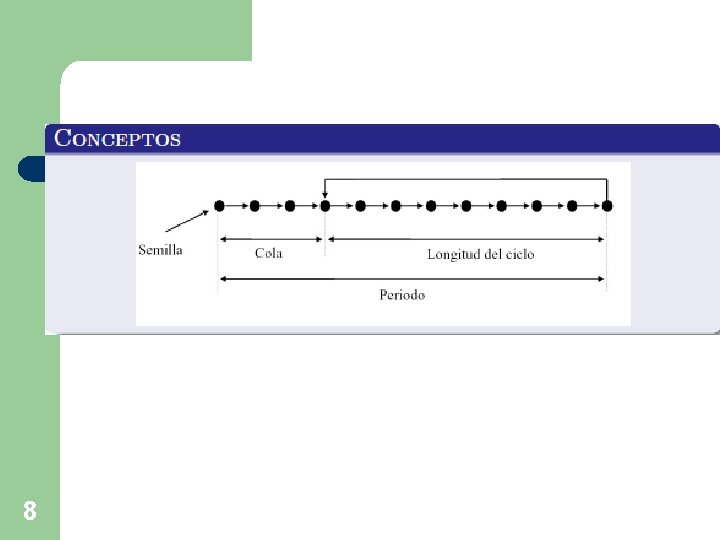
8

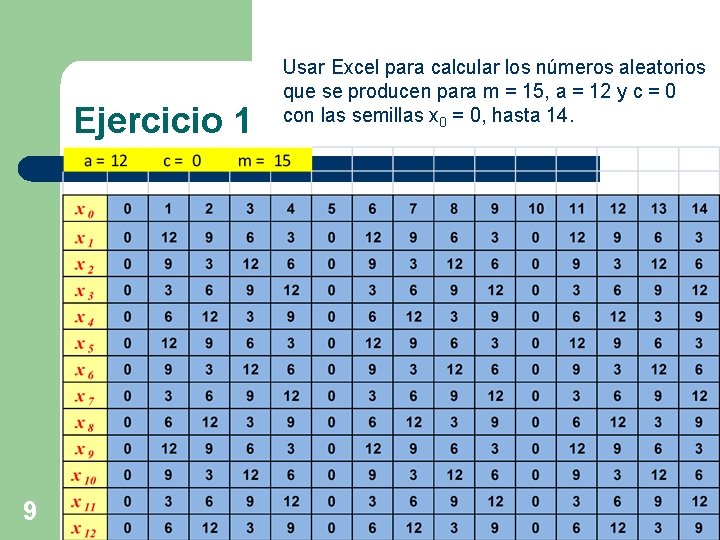
Ejercicio 1 9 Usar Excel para calcular los números aleatorios que se producen para m = 15, a = 12 y c = 0 con las semillas x 0 = 0, hasta 14.

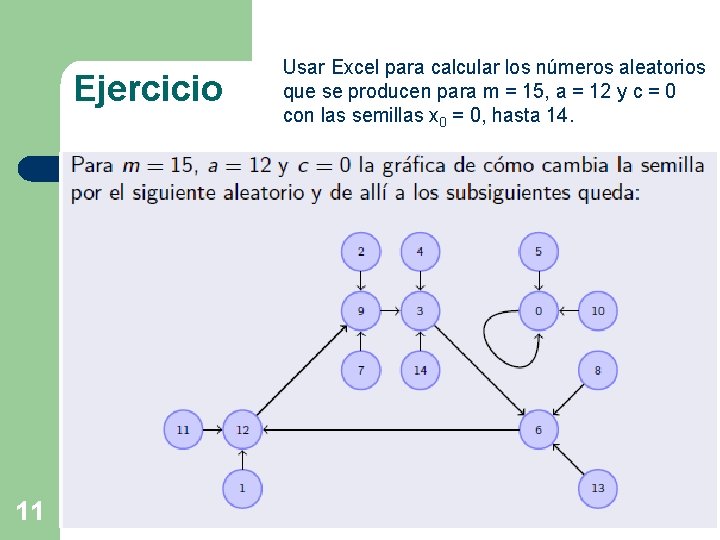
Ejercicio Usar Excel para calcular los números aleatorios que se producen para m = 15, a = 12 y c = 0 con las semillas x 0 = 0, hasta 14. Para x 0 = 1: ¿Cuál es el período, la longitud es del ciclo y la longitud de la cola ? . R: 5, 4, 1. 10

Ejercicio 11 Usar Excel para calcular los números aleatorios que se producen para m = 15, a = 12 y c = 0 con las semillas x 0 = 0, hasta 14.

GCL Multiplicativos Periodo completo = Cuando tiene el máximo periodo posible, m – 1. Los hay con m potencia de 2 (m = 2 k ) que son rápidos pues el residuo en divisiones con potencia de 2 puede hacerse rápidamente. Aunque tienen la desventaja que no son de periodo completo pueden ser suficientes para muchas aplicaciones. 12 Cuando m no es potencia de 2 el generador es menos rápido; se acostumbra elegir un número m que sea primo y la relación entre m y a debe ser especial para que el generador tenga un periodo completo o al menos grande.

13

14

Ejercicio 2 Suponiendo que se utilice el generador de números seudo-aleatorios. y que la semilla se escoge eligiendo al azar un entero entre 1 y 26 − 1 inclusive, determine el promedio de la longitud del periodo y su desviación estándar. 15

Varianza y Desviación Estándar para una muestra de datos. Varianza: Desviación Estándar: 16

Ejercicio 1. Determina el rango, la varianza y la desviación estándar para los siguientes datos: 2 4 3 5 2 2 0 1 R = Rango 5; Varianza 2. 5536 y Desviación Estándar 1. 5980 2. Determina el rango, la varianza y la desviación estándar para los siguientes datos: -2 -4 -3 -5 -2 -2 0 -1 R = Rango 5; Varianza 2. 5536 y Desviación Estándar 1. 5980 17 3. Determina el rango, la varianza y la desviación estándar para los siguientes datos: 6 12 9 15 6 6 0 3 R = Rango 15; Varianza 22. 9821 y Desviación Estándar 4. 7940

Ejercicio Frecuentemente se utilizan generadores de números seudoaleatorios en forma encadenada; por ejemplo, el número que sale de xn+1 = (81 ・xn + 121) mod 255 es utilizado por yn+1 = (625 ・ xn+1 + 48) mod 63 18 para producir el número yn+1 que es el que se reporta. Usando la semilla x 0 = 23 y los datos anteriores, determine los primeros 2 números aleatorios generados (y 1 y y 2).

Otro ejercicio Frecuentemente se utilizan generadores de números seudoaleatorios en forma encadenada; por ejemplo, el número que sale de xn+1 = (45 ・xn + 71) mod 127 es utilizado por yn+1 = (125 ・ xn+1 + 11) mod 63 19 para producir el número yn+1 que es el que se reporta. Usando la semilla x 0 = 49 y los datos anteriores, determine los primeros 2 números aleatorios generados (y 1 y y 2).

Probando generadores de números aleatorios Es importante asegurarse de que el generador usado produzca una secuencia suficientemente aleatoria. Para esto se somete el generador a pruebas estadísticas. Si no pasa una prueba, podemos asumir que el generador es malo. Pasar una prueba es una condición necesaria pero no suficiente. Un generador puede pasar una prueba y luego no pasarla si se usa otra semilla u otro segmento del ciclo. 20

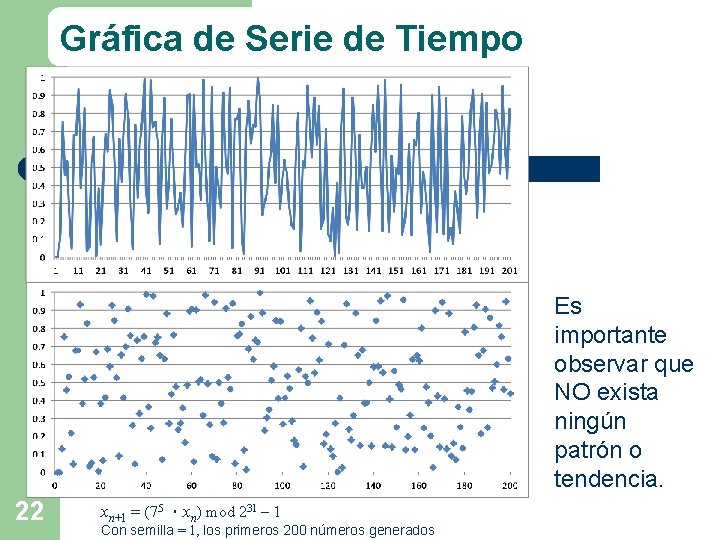
¿Cómo sabemos que nuestro generador es bueno? PRUEBAS GRÁFICAS • Gráfica de Serie de Tiempo. • Tablas de frecuencias e histogramas PRUEBA ESTADÍSTICA • Prueba Ji-cuadrada • Usar el ejemplo: xn+1 = (75 ・xn) mod 231 – 1 Con semilla = 1, los primeros 200 números generados. 21

Gráfica de Serie de Tiempo Es importante observar que NO exista ningún patrón o tendencia. 22 xn+1 = (75 ・xn) mod 231 – 1 Con semilla = 1, los primeros 200 números generados

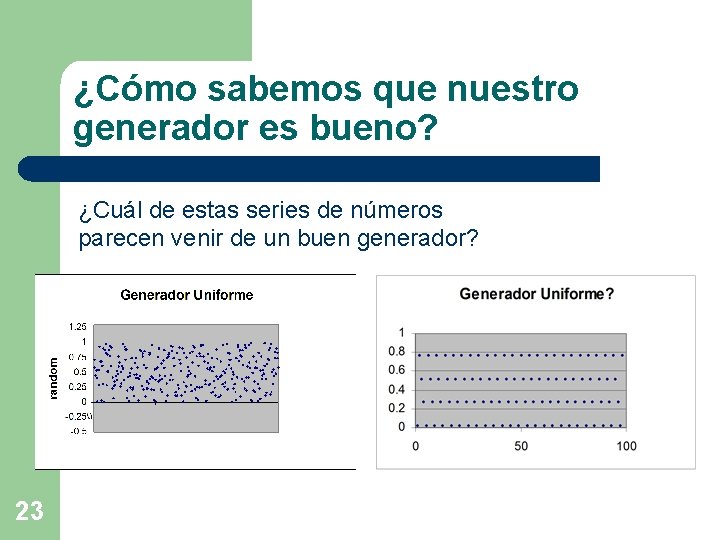
¿Cómo sabemos que nuestro generador es bueno? ¿Cuál de estas series de números parecen venir de un buen generador? 23

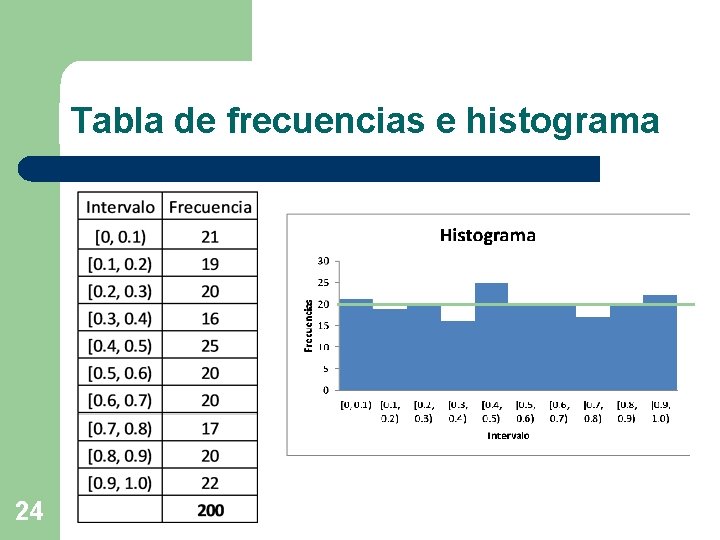
Tabla de frecuencias e histograma 24

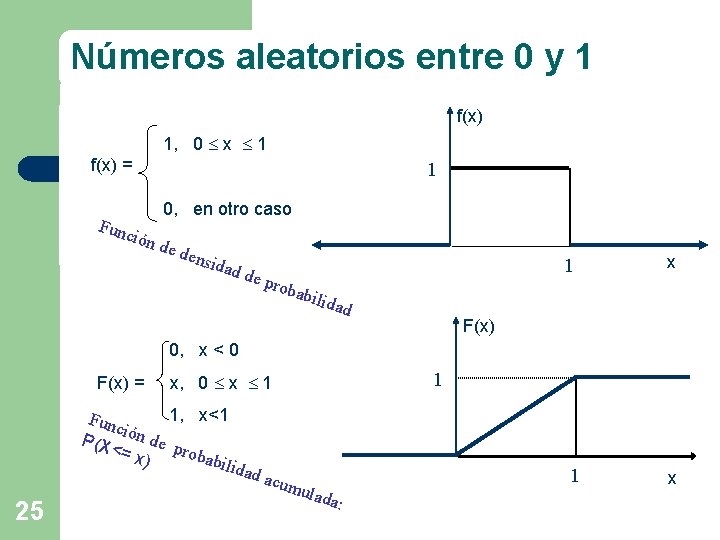
Números aleatorios entre 0 y 1 f(x) 1, 0 x 1 f(x) = 1 Fun 0, en otro caso ción de d ensi dad de p 1 roba x bilid ad F(x) 0, x < 0 1 F(x) = x, 0 x 1 1, x<1 F un ción d P(X <= x e prob abili ) d ad a c 25 umu lada 1 : x

Números aleatorios entre 0 y 1 * La probabilidad de observar un valor en un particular intervalo es independiente del valor previo observado. * Todo punto en el rango tiene igual probabilidad de ser elegido. * Si el intervalo (0, 1) es dividido en n sub-intervalos de igual longitud, el número esperado de observaciones en cada intervalo es N/n. (N número de observaciones totales). El objetivo de cualquier esquema de generación (generador), es producir una secuencia de números entre 0 y 1 que simule las propiedades ideales de distribución uniforme y de independencia. 26

Prueba estadística Ji-cuadrada Esta es la prueba más comúnmente usada. En general, puede ser usada para cualquier distribución. A partir de un histograma, se comparan las frecuencias observadas con las frecuencias obtenidas de la distribución específica (frecuencias esperadas). 27

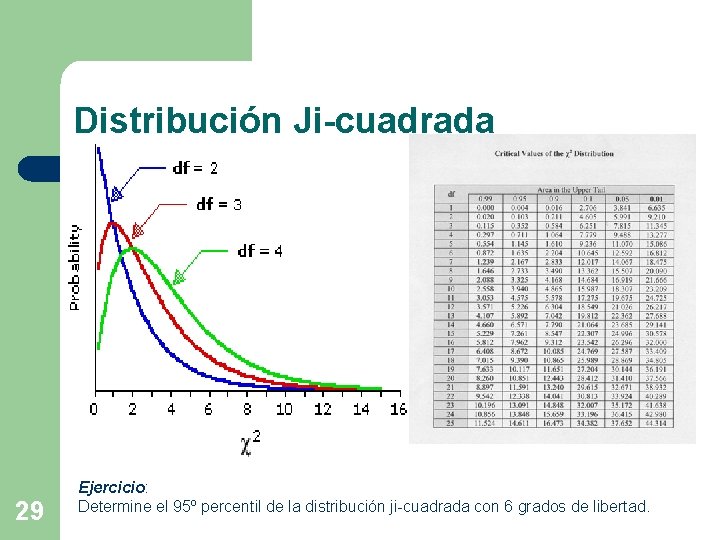
Prueba estadística Ji-cuadrada n Hipótesis nula. Ho: no hay diferencia entre frecuencias observadas y esperadas. n Hipótesis alternativa. Ha o H 1 : existe una diferencia entre frecuencias observadas y esperadas. Estadístico de prueba: 28 Si el ajuste es exacto, c 02 es cero, pero por aleatoriedad no lo será. Se puede demostrar que tiene distribución ji-cuadrado con k-1 grados de libertad.

Distribución Ji-cuadrada 29 Ejercicio: Determine el 95º percentil de la distribución ji-cuadrada con 6 grados de libertad.

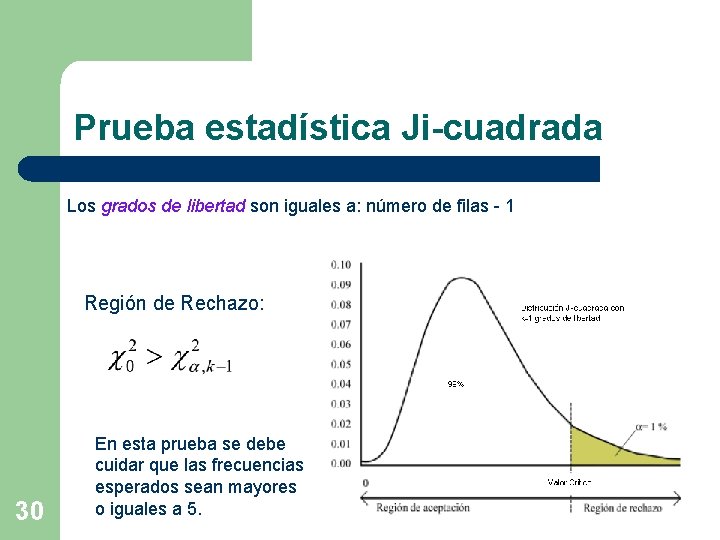
Prueba estadística Ji-cuadrada Los grados de libertad son iguales a: número de filas - 1 Región de Rechazo: 30 En esta prueba se debe cuidar que las frecuencias esperados sean mayores o iguales a 5.

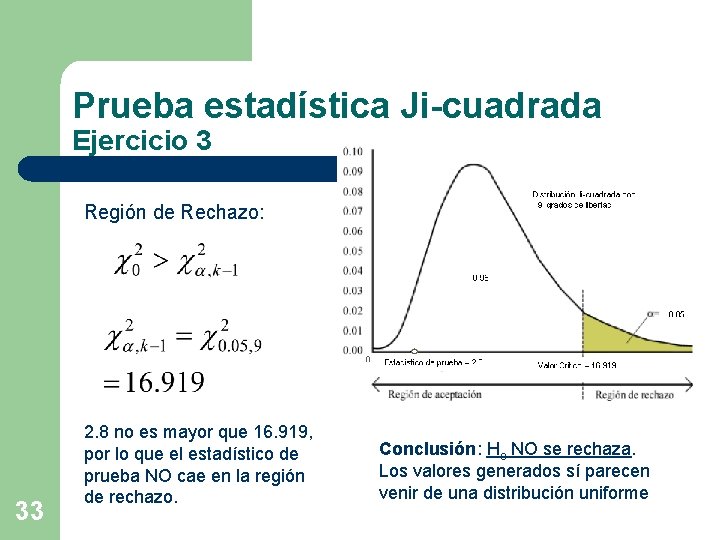
Prueba estadística Ji-cuadrada Ejercicio 3 Generador: xn+1 = (75 ・xn) mod 231 – 1 Con semilla = 1, los primeros 200 números generados. Realizar la prueba estadística ji-cuadrada para probar si los valores vienen de una distribución uniforme. Usar nivel de significancia = 0. 05 n Ho: Los valores provienen de una distribución uniforme. n Ha: Los valores NO provienen de una distribución uniforme. 31

Prueba estadística Ji-cuadrada Ejercicio 3 Estadístico de prueba 32

Prueba estadística Ji-cuadrada Ejercicio 3 Región de Rechazo: 33 2. 8 no es mayor que 16. 919, por lo que el estadístico de prueba NO cae en la región de rechazo. Conclusión: Ho NO se rechaza. Los valores generados sí parecen venir de una distribución uniforme

Ejercicio 4 Generador: xn+1 = (57 ・xn) mod 215 – 1 Con semilla = 1, considere los primeros 100 números generados entre 0 y 1. Realizar la prueba estadística ji-cuadrada para probar si los valores vienen de una distribución uniforme. Usar 10 intervalos. Usar nivel de significancia = 0. 05. 34

Ejercicio 5 Usando el método del cuadrado medio y semilla = 5896, se generaron los primeros 80 números aleatorios. Realizar la prueba estadística jicuadrada para probar si los valores provienen de una distribución uniforme. Usar 8 intervalos y un nivel de significancia = 0. 05. 35

Ejercicio 6 Generador: xn+1 = (57 ・xn) mod 215 – 1 Con semilla = 14, considere los primeros 100 números generados entre 0 y 1. Realizar la prueba estadística ji-cuadrada para probar si los valores vienen de una distribución uniforme. Usar 8 intervalos. Usar nivel de significancia = 0. 05. 36

Generación de variables aleatorias discretas Suponga que un determinado fenómeno aleatorio tiene la siguiente distribución de probabilidad: 37 0 R 0. 3 entonces x = 18 grs. 0. 3 < R 0. 7 entonces x = 19 grs. 0. 7 < R 1 entonces x = 20 grs. Para esto, se necesitan números aleatorios R entre 0 y 1.

Ejercicio 7 Usar el generador: xn+1 = (57 ・xn) mod 215 – 1 Con semilla = 1. a) Generar 100 valores de la distribución: 38 b) Utilizar la prueba ji-cuadrada para decidir si los valores generados realmente parecen tener la distribución de probabilidad anterior (a = 0. 05). c) Usar 20 semillas y observar en cuántos casos la prueba se rechaza.

Números aleatorios con distribución normal En Excel. =NORMINV(RAND(), 500, 50) aleatorio entre 0 y 1 media desv. std. (puedes usar tu propio generador) 39

Ejercicio 8 Usar el generador: xn+1 = (59 ・xn) mod 217 – 1 Con semilla = matrícula menor del equipo. a) Generar 500 valores de la distribución uniforme continua entre 0 y 1 con el generador. b) Usar esos valores para generar 500 números aleatorios de la distribución normal con media 100 y desviación estándar 16 (distribución del puntaje de IQ). c) Utilizar la prueba ji-cuadrada para decidir si los valores generados realmente parecen tener la distribución normal (a = 0. 01). En la tabla de frecuencias, calcular a mano 3 frecuencias esperadas (mostrar procedimiento usando editor de ecuaciones). Escribir conclusión (sí o no se trata de un buen generador de números normales). d) Construir el histograma de frecuencias observadas y el histograma de frecuencias esperadas. 40 e) Usar 20 semillas y observar en cuántos casos la prueba se rechaza. Indicar qué semillas se usaron y cuál fue el valor del estadístico en cada caso.
 Generacin del 27
Generacin del 27 Generacin del 27
Generacin del 27 Numeros pentagonales
Numeros pentagonales Numero romano ivx
Numero romano ivx Temporalidad de los romanos
Temporalidad de los romanos Nmeros naturales
Nmeros naturales Ejercicios con numeros romanos
Ejercicios con numeros romanos Yu chi ho
Yu chi ho Ordenar numeros enteros
Ordenar numeros enteros Nmeros enteros
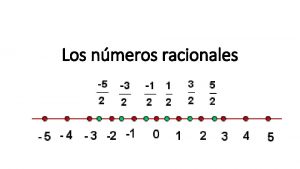
Nmeros enteros Nmeros reales
Nmeros reales Nmeros primos
Nmeros primos Nmeros ordinales
Nmeros ordinales Nmeros reales
Nmeros reales Nmeros romanos
Nmeros romanos Algarismo cardinal
Algarismo cardinal Nmeros ordinales
Nmeros ordinales Nmeros enteros
Nmeros enteros Nmeros naturales
Nmeros naturales Nmeros ordinales
Nmeros ordinales Nmeros enteros
Nmeros enteros Los nmeros
Los nmeros Primero segundo tersero
Primero segundo tersero Divisível por 7
Divisível por 7 Ninguna autoridad tendrias sobre mi
Ninguna autoridad tendrias sobre mi Hebreos 15 12
Hebreos 15 12 Palabras corrompidas
Palabras corrompidas Que ninguna familia comience en cualquier de repente
Que ninguna familia comience en cualquier de repente Ninguna arma forjada
Ninguna arma forjada