Fuzzy sets II Prof Dr Jaroslav Ramk Fuzzy

Fuzzy sets II Prof. Dr. Jaroslav Ramík Fuzzy sets II 1

Content • • Extension principle Extended binary operations with fuzzy numbers Extended operations with L-R fuzzy numbers Extended operations with t-norms Probability, possibility and fuzzy measure Probability and possibility of fuzzy event Fuzzy sets of the 2 nd type Fuzzy relations Fuzzy sets II 2

Extension principle (EP) by L. Zadeh, 1965 • EP makes possible to extend algebraical operations with NUMBERS to FUZZY SETS • Even more: EP makes possible to extend REAL FUNCTIONS of real variables to FUZZY FUNCTIONS with fuzzy variables • Even more: EP makes possible to extend CRISP CONCEPTS to FUZZY CONCEPTS (e. g. relations, convergence, derivative, integral, etc. ) Fuzzy sets II 3

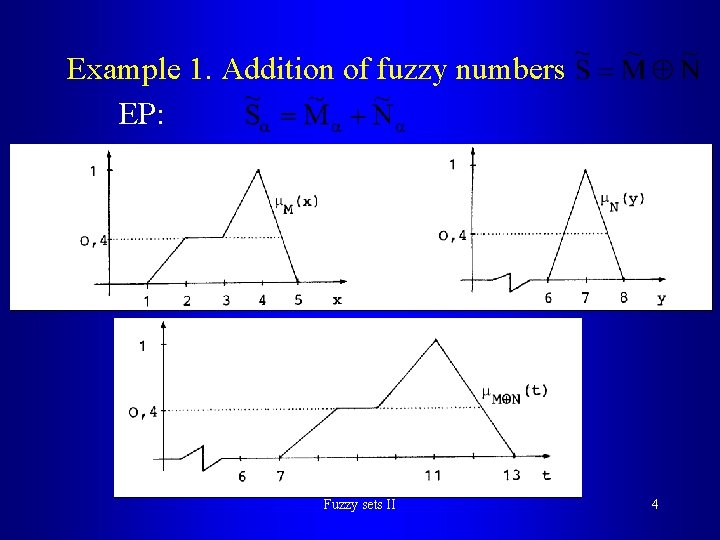
Example 1. Addition of fuzzy numbers EP: Fuzzy sets II 4

Theorem 1. Let • the operation denotes + or · (add or multiply) • - fuzzy numbers, [0, 1] • - -cuts Then is defined by its -cuts as follows [0, 1] Fuzzy sets II 5

Extension principle for functions • X 1, X 2, …, Xn, Y - sets • n - fuzzy sets on Xi , i = 1, 2, …, n • g : X 1 X 2 … Xn Y - function of n variables i. e. (x 1, x 2 , …, xn ) y = g (x 1, x 2 , …, xn ) Then the extended function is defined by Fuzzy sets II 6

Remarks • g-1(y) = {(x 1, x 2 , …, xn ) | y = g (x 1, x 2 , …, xn )} - co-image of y • Special form of EP: g (x 1, x 2) = x 1+x 2 or g (x 1, x 2) = x 1*x 2 • Instead of Min any t-norm T can be used - more general for of EP Fuzzy sets II 7

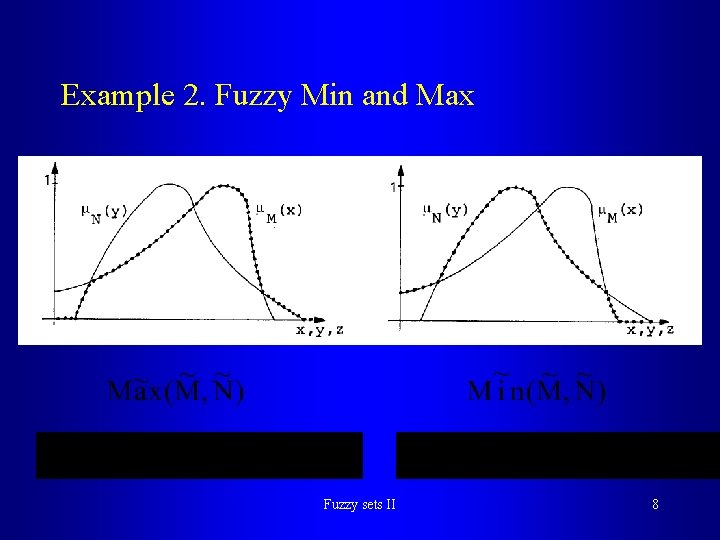
Example 2. Fuzzy Min and Max Fuzzy sets II 8

Extended operations with L-R fuzzy numbers • L, R : [0, + ) [0, 1] - decreasing functions shape Left spread Right spread • L(0) = R(0) = 1, m - main value, > 0 • = (m, , )LR - fuzzy number of L-R-type if • Fuzzy sets II 9

Example 3. L-R fuzzy number “About eight” Fuzzy sets II 10

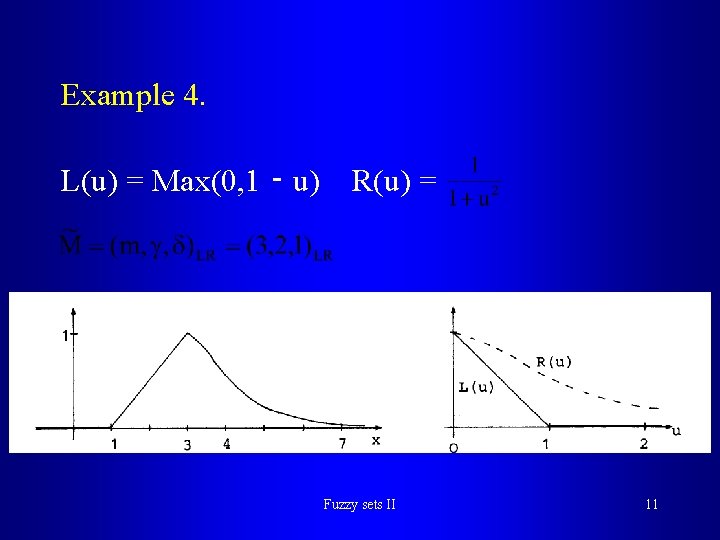
Example 4. L(u) = Max(0, 1 ‑ u) R(u) = Fuzzy sets II 11

Addition Theorem 2. Let = (m, , )LR , = (n, , )LR where L, R are shape functions Then is defined as Example: (2, 3, 4)LR (1, 2, 3)LR = (3, 5, 7)LR Fuzzy sets II 12

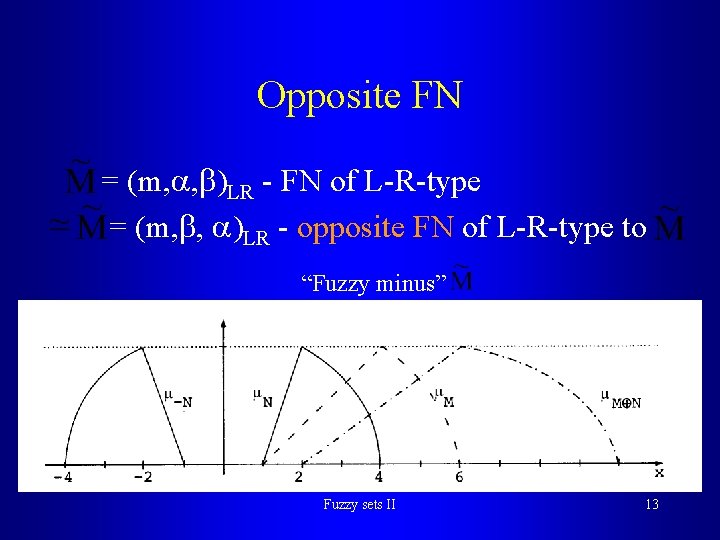
Opposite FN = (m, , )LR - FN of L-R-type = (m, , )LR - opposite FN of L-R-type to “Fuzzy minus” Fuzzy sets II 13

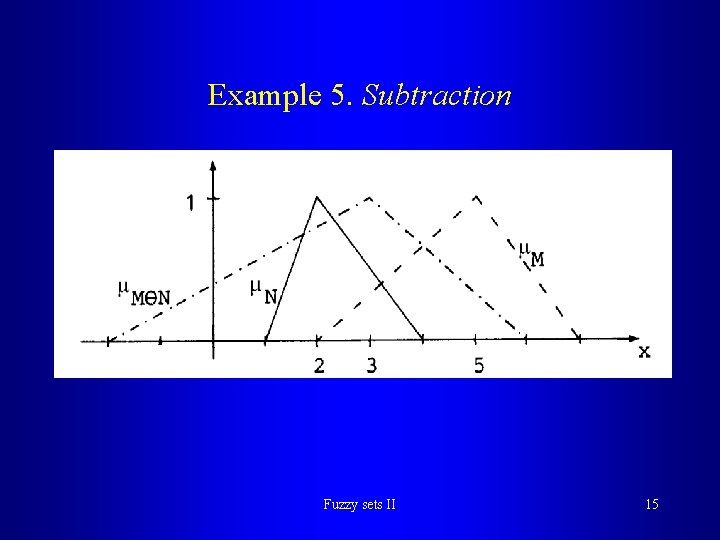
Subtraction Theorem 3. Let = (m, , )LR , = (n, , )LR where L, R are shape functions Then is defined as Example: (2, 3, 4)LR (1, 2, 3)LR = (1, 6, 6)LR Fuzzy sets II 14

Example 5. Subtraction Fuzzy sets II 15

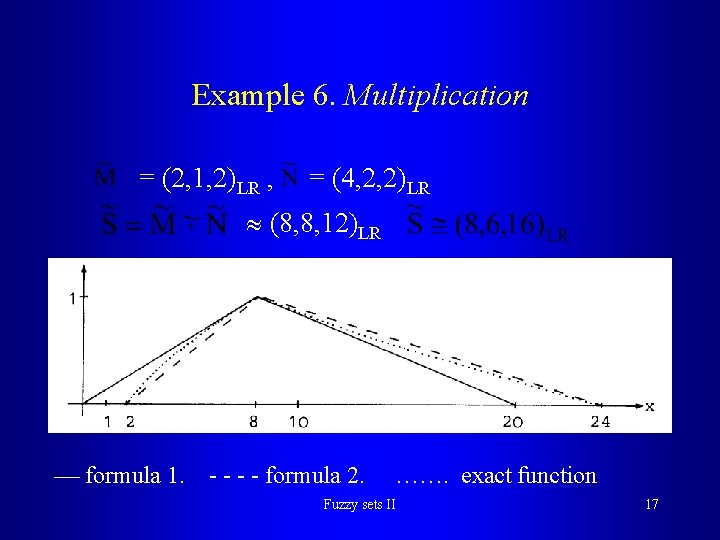
Multiplication Theorem 4. Let = (m, , )LR , = (n, , )LR where L, R are shape functions Then is defined by approximate formulae: 1. 2. Example by 1. : (2, 3, 4)LR (1, 2, 3)LR (2, 7, 10)LR Fuzzy sets II 16

Example 6. Multiplication = (2, 1, 2)LR , = (4, 2, 2)LR (8, 8, 12)LR formula 1. - - formula 2. ……. exact function Fuzzy sets II 17

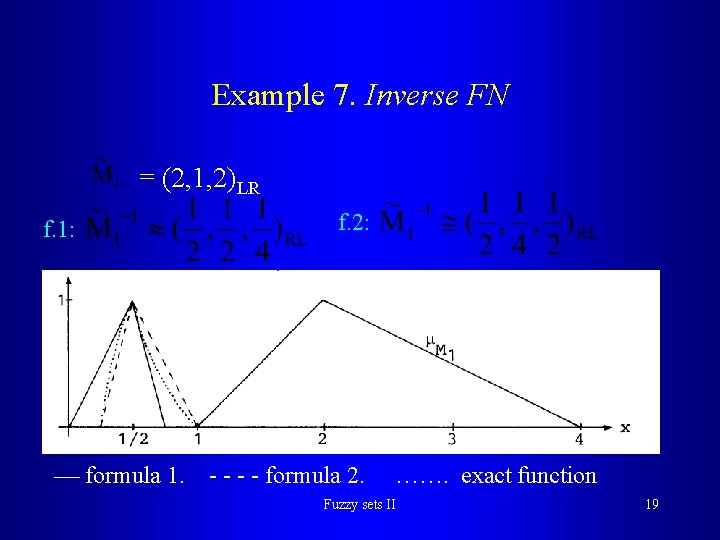
Inverse FN = (m, , )LR > 0 - FN of L-R-type - approximate formula 1 - approximate formula 2 We define inverse FN only for positive (or negative) FN ! Fuzzy sets II 18

Example 7. Inverse FN = (2, 1, 2)LR f. 1: formula 1. f. 2: - - formula 2. ……. exact function Fuzzy sets II 19

Division = (m, , )LR , = (n, , )LR > 0 where L, R are shape functions Define Combinations of approximate formulae, e. g. Fuzzy sets II 20

Probability, possibility and fuzzy measure Sigma Algebra ( -Algebra) on : F - collection of classical subsets of the set satisfying: (A 1) F (A 2) if A F then CA F (A 3) if Ai F, i = 1, 2, . . . then i Ai F - elementary space (space of outcomes - elementary events) F - -Algebra of events of Fuzzy sets II 21

Probability measure F - -Algebra of events of p : F [0, 1] - probability measure on F satisfying: (W 1) if A F then p(A) 0 (W 2) p( ) = 1 (W 3) if Ai F , i = 1, 2, . . . , Ai Aj = , i j then p( i Ai ) = i p(Ai ) - -additivity (W 3*) if A, B F , A B= , then p(A B ) = p(A ) + p(B) - additivity Fuzzy sets II 22

Fuzzy measure F - -Algebra of events of g : F [0, 1] - fuzzy measure on F satisfying: (FM 1) p( ) = 0 (FM 2) p( ) = 1 (FM 3) if A, B F , A B then p(A) p(B) - monotonicity (FM 4) if A 1, A 2, . . . F , A 1 A 2 . . . then g(Ai ) = g( Ai ) - continuity Fuzzy sets II 23

Properties • Additivity condition (W 3) is stronger than monotonicity (MP 3) & continuity (MP 4) i. e. • (W 3) (MP 3) & (MP 4) • Consequence: Any probability measure is a fuzzy measure but not contrary Fuzzy sets II 24

Possibility measure P( ) - Power set of (st of all subsets of ) : P( ) [0, 1] - possibility measure on satisfying: (P 1) ( ) = 0 (P 2) ( ) = 1 (P 3) if Ai P( ) , i = 1, 2, . . . then ( i Ai ) = Supi {p(Ai )} (P 3*) if A, B P( ) , then (A B ) = Max{ (A ), (B)} Fuzzy sets II 25

Properties • Condition (P 3) is stronger than monotonicity (MP 3) & continuity (MP 4) i. e. • (P 3) (MP 3) & (MP 4) • Consequence: Any possibility measure is a fuzzy measure but not contrary Fuzzy sets II 26

Example 8. = A B C F = { , A, B, C, A B, B C, A B C} Fuzzy sets II 27

Possibility distribution • - possibility measure on P( ) • Function : [0, 1] defined by (x) = ({x}) for x is called a possibility distribution on Interpretation: is a membership function of a fuzzy set , i. e. (x) = A(x) x , A(x) is the possibility that x belongs to Fuzzy sets II 28

Probability and possibility of fuzzy event Example 1: What is the possibility (probability) that tomorrow will be a nice weather ? Example 2: What is the possibility (probability) that the profit of the firm A in 2003 will be high ? • nice weather, high profit - fuzzy events Fuzzy sets II 29

Probability of fuzzy event Finite universe ={x 1, …, xn} - finite set of elementary outcomes F - -Algebra on P - probability measure on F - fuzzy set of , with the membership function A(x) - fuzzy event, A F for [0, 1] P( ) = - probability of fuzzy event Fuzzy sets II 30

Probability of fuzzy event Real universe = R - real numbers - set of elementary outcomes F - -Algebra on R P - probability measure on F given by density fction g - fuzzy set of R, with the membership function A(x) - fuzzy event A F for [0, 1] P( ) = - probability of fuzzy event Fuzzy sets II 31

Example 9. = (4, 1, 2)LR L(u) = R(u) = e-u - “around 4” - density function of random value = 0, 036 Fuzzy sets II 32

Possibility of fuzzy event - set of elementary outcomes : [0, 1] - possibility distribution - fuzzy set of , with the membership function A(x) - fuzzy event A F for [0, 1] P( ) = - possibility of fuzzy event Fuzzy sets II 33

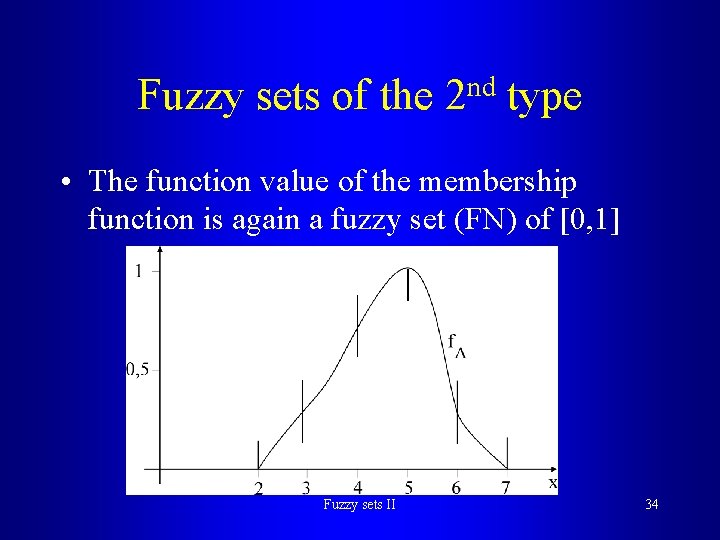
Fuzzy sets of the nd 2 type • The function value of the membership function is again a fuzzy set (FN) of [0, 1] Fuzzy sets II 34

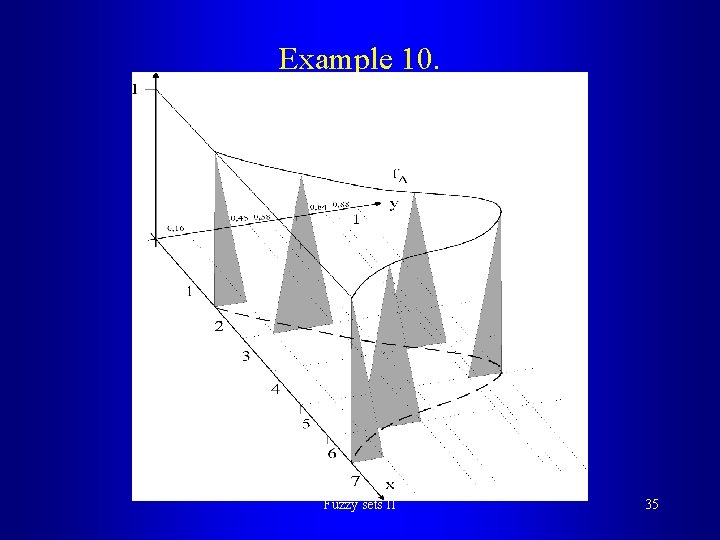
Example 10. Fuzzy sets II 35

Example 11. Linguistic variable “Stature”- Height of the body Fuzzy sets II 36

Fuzzy relations • X - universe • - (binary) fuzzy (valued) relation on X = fuzzy set on X X is given by the membership function R : X X [0, 1] FR is: • Reflexive: R (x, x) = 1 x X • Symmetric: R (x, y) = R (y, x) x, y X • Transitive: Supz[Min{ R (x, z), R (z, y)}] R (x, y) • Equivalence: reflexive & symmetric & transitive Fuzzy sets II 37

Example 12. Binary fuzzy relation : “x is much greater than y” e. g. R(8, 1) = 7/9 = 0, 77… - is antisymmetric: If R (x, y) > 0 then R (y, x) = 0 x, y X Fuzzy sets II 38

Example 13. Binary fuzzy relation : “x is similar to y” X = {1, 2, 3, 4, 5} x/y 1 2 3 4 5 1 1, 0 0, 5 0, 3 0, 2 0, 5 1, 0 0, 6 0, 5 0, 2 3 0, 6 1, 0 0, 7 0, 4 4 0, 2 0, 5 0, 7 1, 0 0, 4 5 0 0, 2 0, 4 0, 8 1, 0 is equivalence ! Fuzzy sets II 39

Summary • • Extension principle Extended binary operations with fuzzy numbers Extended operations with L-R fuzzy numbers Extended operations with t-norms Probability, possibility and fuzzy measure Probability and possibility of fuzzy event Fuzzy sets of the 2 nd type Fuzzy relations Fuzzy sets II 40

References [1] J. Ramík, M. Vlach: Generalized concavity in fuzzy optimization and decision analysis. Kluwer Academic Publ. Boston, Dordrecht, London, 2001. [2] H. -J. Zimmermann: Fuzzy set theory and its applications. Kluwer Academic Publ. Boston, Dordrecht, London, 1996. [3] H. Rommelfanger: Fuzzy Decision Support - Systeme. Springer - Verlag, Berlin Heidelberg, New York, 1994. [4] H. Rommelfanger, S. Eickemeier: Entscheidungstheorie - Klassische Konzepte und Fuzzy Erweiterungen, Springer - Verlag, Berlin Heidelberg, New York, 2002. Fuzzy sets II 41