Fuzzy Logic Approximate Reasoning 1 Fuzzy Sets Fuzzy

Fuzzy Logic & Approximate Reasoning 1

Fuzzy Sets Fuzzy Logic & Approximate Reasoning 2

References • Journal: – – – • Conferences: – – – • IEEE Trans. on Fuzzy Systems. Fuzzy Sets and Systems. Journal of Intelligent & Fuzzy Systems International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems . . . IEEE Conference on Fuzzy Systems. IFSA World Congress. . Books and Papers: – – – – Z. Chi et al, Fuzzy Algorithms with applications to Image Processing and Pattern Recognition, World Scientific, 1996. S. N. Sivanandam, Introduction to Fuzzy Logic using MATLAB, Springer, 2007. J. M. Mendel, Fuzzy Logic Systems for Engineering: A toturial, IEEE, 1995. W. Siler, FUZZY EXPERT SYSTEMS AND FUZZY REASONING, John Wiley Sons, 2005 G. Klir, Uncertainty and Informations, John Wiley Sons, 2006. L. A. Zadeh, Fuzzy sets, Information and control, 8, 338 -365, 1965. L. A. Zadeh, The Concept of a Linguistic Variable and its Application to Approximate Reasoning-I, III, Information Science 8, 1975 L. A. Zadeh, Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic, Fuzzy Sets and Systems 90(1997), 111 -127. . . . http: //www. type 2 fuzzylogic. org/ IEEE Computational Intelligence Society http: //ieee-cis. org/ International Fuzzy Systems Association http: //www. isc. meiji. ac. jp/~ifsatkym/ Fuzzy Logic & Approximate 3 J. M. Mendel http: //sipi. usc. edu/~mendel Reasoning

Contents • • • Fuzzy sets. Fuzzy Relations and Fuzzy reasoning Fuzzy Inference Systems Fuzzy Clustering Fuzzy Expert Systems Applications: Image Processing, Robotics, Control. . . Fuzzy Logic & Approximate Reasoning 4

Fuzzy Sets: Outline • Introduction: History, Current Level and Further Development of Fuzzy Logic Technologies in the U. S. , Japan, and Europe • Basic definitions and terminology • Set-theoretic operations • MF formulation and parameterization – MFs of one and two dimensions – Derivatives of parameterized MFs • More on fuzzy union, intersection, and complement – Fuzzy intersection and union – Parameterized T-norm and T-conorm • Fuzzy Number • Fuzzy Relations Fuzzy Logic & Approximate Reasoning 5

History, State of the Art, and Future Development 1965 Seminal Paper “Fuzzy Logic” by Prof. Lotfi Zadeh, Faculty in Electrical Engineering, U. C. Berkeley, Sets the Foundation of the “Fuzzy Set Theory” 1970 First Application of Fuzzy Logic in Control Engineering (Europe) 1975 Introduction of Fuzzy Logic in Japan 1980 Empirical Verification of Fuzzy Logic in Europe 1985 Broad Application of Fuzzy Logic in Japan 1990 Broad Application of Fuzzy Logic in Europe 1995 Broad Application of Fuzzy Logic in the U. S. 1998 Type-2 Fuzzy Systems 2000 Fuzzy Logic Becomes a Standard Technology and Is Also Applied in Data and Sensor Signal Analysis. Application of Fuzzy Logic in Business and Finance. Fuzzy Logic & Approximate Reasoning 6

Types of Uncertainty and the Modeling of Uncertainty Stochastic Uncertainty: X The Probability of Hitting the Target Is 0. 8 Lexical Uncertainty: X "Tall Men", "Hot Days", or "Stable Currencies" X We Will Probably Have a Successful Business Year. X The Experience of Expert A Shows That B Is Likely to Occur. However, Expert C Is Convinced This Is Not True. Most Words and Evaluations We Use in Our Daily Reasoning Are Not Clearly Defined in a Mathematical Manner. This Allows Humans to Reason on an Abstract Level! Fuzzy Logic & Approximate Reasoning 7

Possible Sources of Uncertainty and Imprecision • There are many sources of uncertainty facing any control system in dynamic real world unstructured environments and real world applications; some sources of these uncertainties are as follows: – Uncertainties in the inputs of the system due to: • The sensors measurements being affected by high noise levels from various sources such a electromagnetic and radio frequency interference, vibration, etc. • The input sensors being affected by the conditions of observation (i. e. their characteristics can be changed by the environmental conditions such as wind, sunshine, humidity, rain, etc. ). Fuzzy Logic & Approximate Reasoning 8

Possible Sources of Uncertainty and Imprecision • Other sources of Uncertainties include: – Uncertainties in control outputs which can result from the change of the actuators characteristics due to wear and tear or due to environmental changes. – Linguistic uncertainties as words mean different things to different people. – Uncertainties associated with the change in the operation conditions due to varying load and environment conditions. Fuzzy Logic & Approximate Reasoning 9

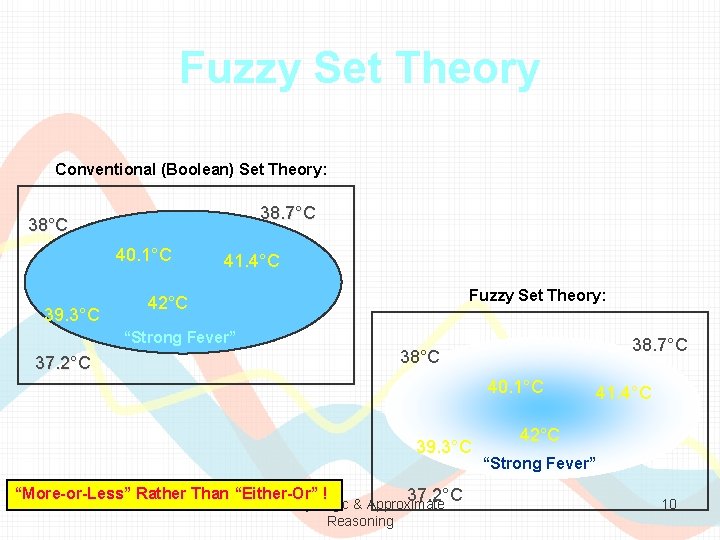
Fuzzy Set Theory Conventional (Boolean) Set Theory: 38. 7°C 38°C 40. 1°C 39. 3°C 41. 4°C Fuzzy Set Theory: 42°C “Strong Fever” 38. 7°C 38°C 37. 2°C 40. 1°C 39. 3°C “More-or-Less” Rather Than “Either-Or” ! 37. 2°C Fuzzy Logic & Approximate Reasoning 41. 4°C 42°C “Strong Fever” 10

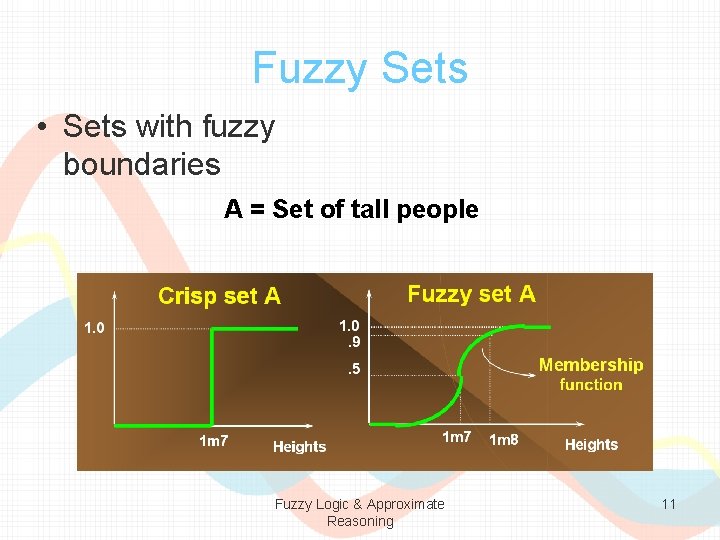
Fuzzy Sets • Sets with fuzzy boundaries A = Set of tall people Fuzzy Logic & Approximate Reasoning 11

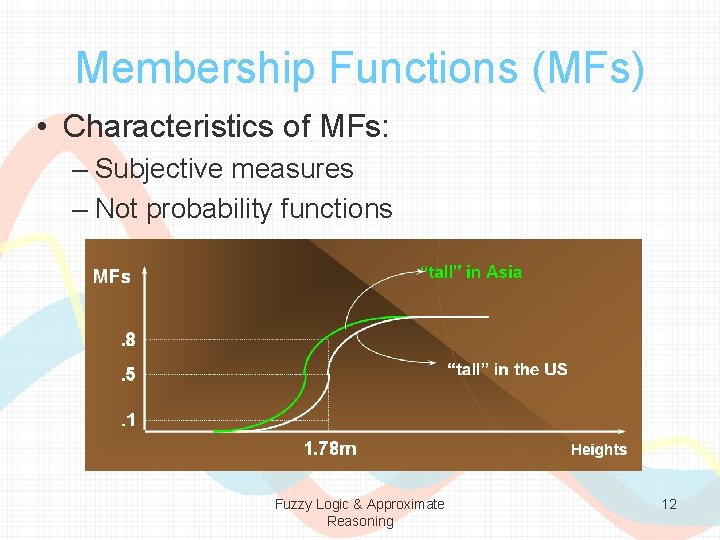
Membership Functions (MFs) • Characteristics of MFs: – Subjective measures – Not probability functions Fuzzy Logic & Approximate Reasoning 12

Fuzzy Sets • A fuzzy set A is characterized by a member set function (MF), A, mapping the elements of A to the unit interval [0, 1]. • Formal definition: A fuzzy set A in X is expressed as a set of ordered pairs: Fuzzy set Membership function (MF) Fuzzy Logic & Approximate Reasoning Universe or universe of discourse 13

Fuzzy Sets with Discrete Universes • Fuzzy set C = “desirable city to live in” X = {SF, Boston, LA} (discrete and non-ordered) C = {(SF, 0. 9), (Boston, 0. 8), (LA, 0. 6)} • Fuzzy set A = “sensible number of children” X = {0, 1, 2, 3, 4, 5, 6} (discrete universe) A = {(0, . 1), (1, . 3), (2, . 7), (3, 1), (4, . 6), (5, . 2), (6, . 1)} Fuzzy Logic & Approximate Reasoning 14

Fuzzy Sets with Cont. Universes • Fuzzy set C = “desirable city to live in” X = {SF, Boston, LA} (discrete and non-ordered) C = {(SF, 0. 9), (Boston, 0. 8), (LA, 0. 6)} • Fuzzy set A = “sensible number of children” X = {0, 1, 2, 3, 4, 5, 6} (discrete universe) A = {(0, . 1), (1, . 3), (2, . 7), (3, 1), (4, . 6), (5, . 2), (6, . 1)} Fuzzy Logic & Approximate Reasoning 15

Alternative Notation • A fuzzy set A can be alternatively denoted as follows: X is discrete X is continuous Note that S and integral signs stand for the union of membership grades; “/” stands for a marker and does not imply division. Fuzzy Logic & Approximate 16 Reasoning

Fuzzy Partition • Fuzzy partitions formed by the linguistic values “young”, “middle aged”, and “old”: Fuzzy Logic & Approximate Reasoning 17

Linguistic Variables • A linguistic variable is a variable whose values are not numbers but words or sentences in a natural or artificial language (Zadeh, 1975 a, p. 201) • Linguistic variable is characterized by [c , T(c), U], in which c : name of the variable, T(c) : the term set of c , universe of discourse U A Linguistic Variable Defines a Concept of Our Everyday Language! Fuzzy Logic & Approximate Reasoning 18

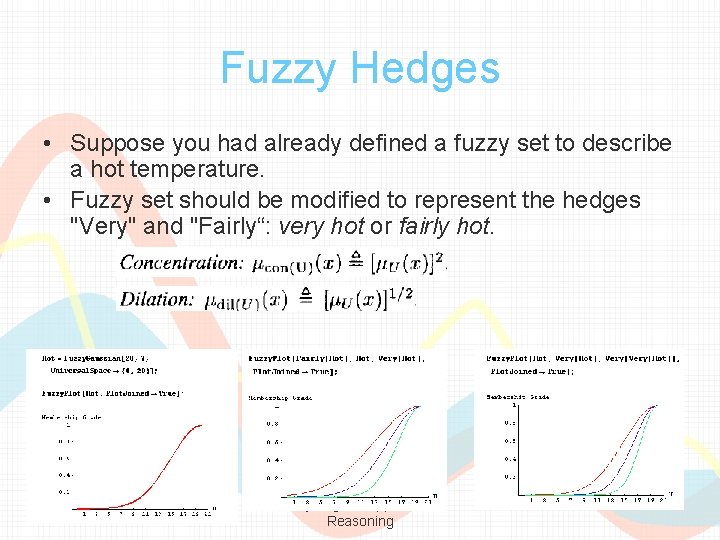
Fuzzy Hedges • Suppose you had already defined a fuzzy set to describe a hot temperature. • Fuzzy set should be modified to represent the hedges "Very" and "Fairly“: very hot or fairly hot. Fuzzy Logic & Approximate Reasoning 19

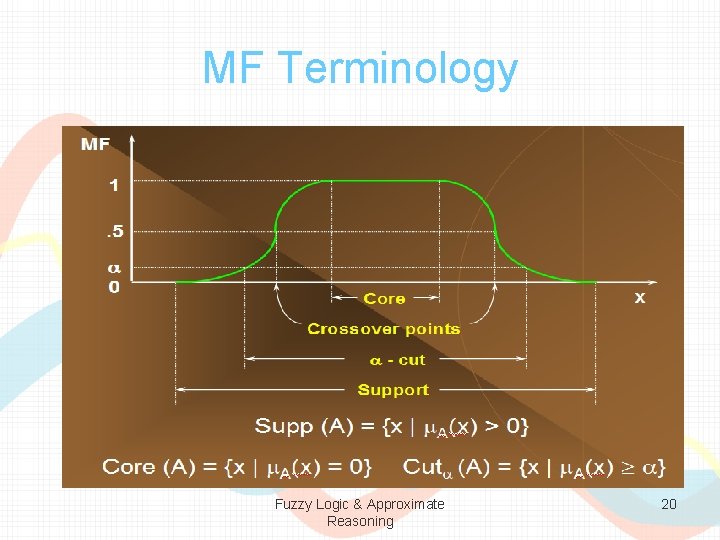
MF Terminology Fuzzy Logic & Approximate Reasoning 20

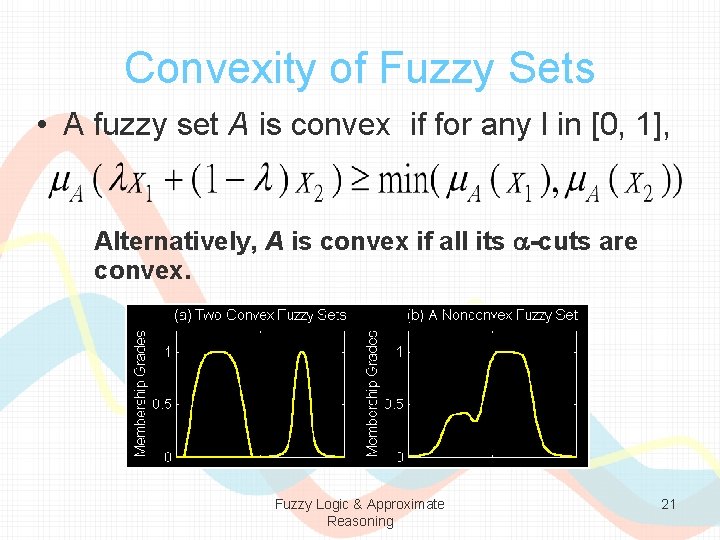
Convexity of Fuzzy Sets • A fuzzy set A is convex if for any l in [0, 1], Alternatively, A is convex if all its a-cuts are convex. Fuzzy Logic & Approximate Reasoning 21

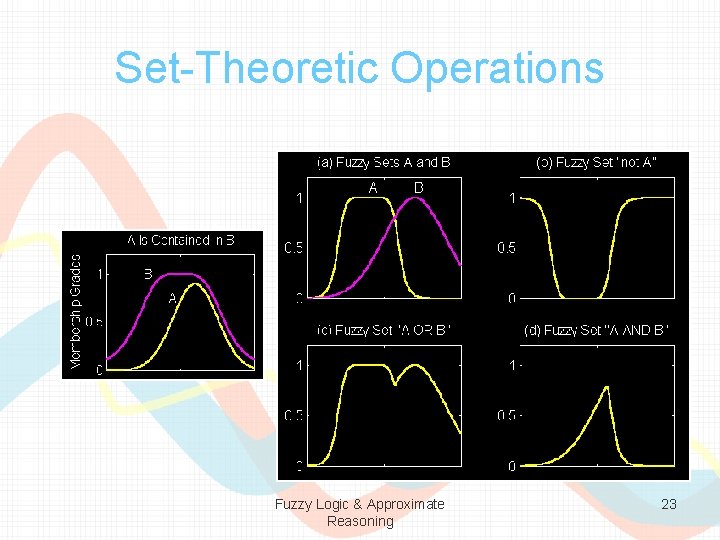
Set-Theoretic Operations • Subset: • Complement: • Union: • Intersection: Fuzzy Logic & Approximate Reasoning 22

Set-Theoretic Operations Fuzzy Logic & Approximate Reasoning 23

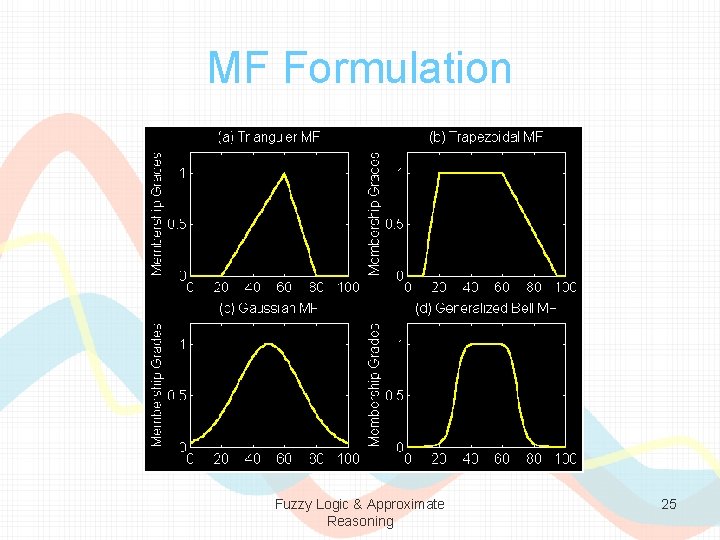
MF Formulation • Triangular MF: Trapezoidal MF: Gaussian MF: Generalized bell MF: Fuzzy Logic & Approximate Reasoning 24

MF Formulation Fuzzy Logic & Approximate Reasoning 25

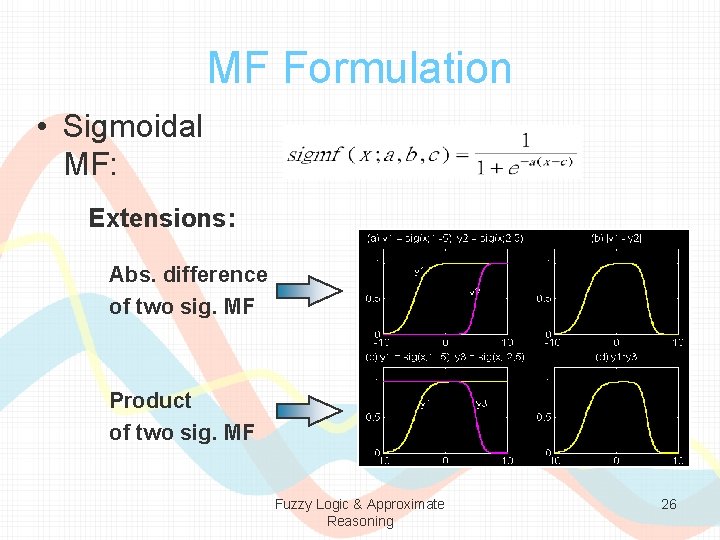
MF Formulation • Sigmoidal MF: Extensions: Abs. difference of two sig. MF Product of two sig. MF Fuzzy Logic & Approximate Reasoning 26

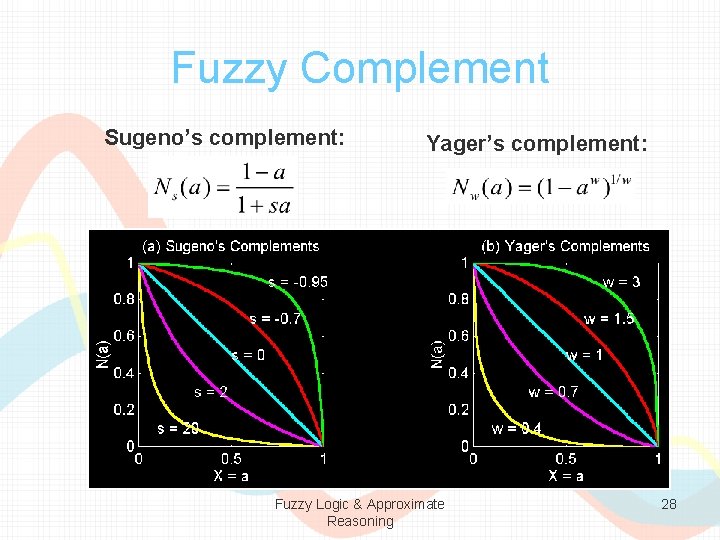
Fuzzy Complement • General requirements: – Boundary: N(0)=1 and N(1) = 0 – Monotonicity: N(a) > N(b) if a < b – Involution: N(N(a) = a • Two types of fuzzy complements: – Sugeno’s complement: – Yager’s complement: Fuzzy Logic & Approximate Reasoning 27

Fuzzy Complement Sugeno’s complement: Yager’s complement: Fuzzy Logic & Approximate Reasoning 28

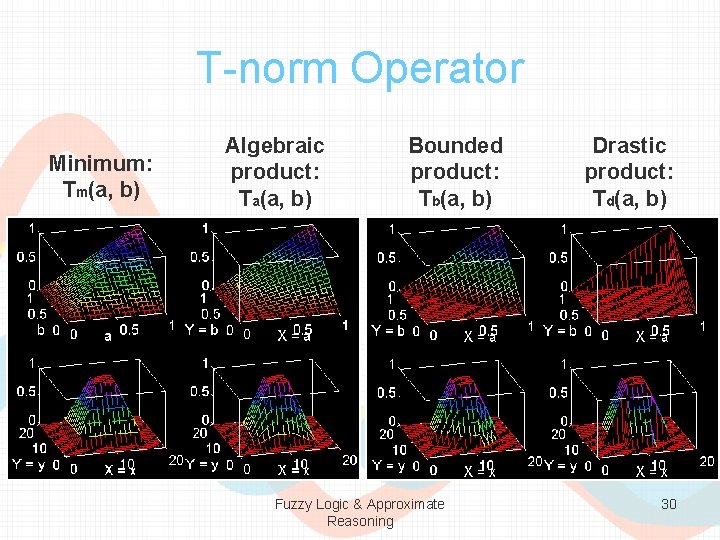
Fuzzy Intersection: T-norm • Basic requirements: – Boundary: T(0, 0) = 0, T(a, 1) = T(1, a) = a – Monotonicity: T(a, b) < T(c, d) if a < c and b < d – Commutativity: T(a, b) = T(b, a) – Associativity: T(a, T(b, c)) = T(T(a, b), c) • Four examples: – Minimum: Tm(a, b) = min{a, b}. – Algebraic product: Ta(a, b) = a. b – Bounded product: Tb(a, b) = max{0, a+b-1} – Drastic product: Td(a, b) Fuzzy Logic & Approximate Reasoning 29

T-norm Operator Minimum: Tm(a, b) Algebraic product: Ta(a, b) Bounded product: Tb(a, b) Fuzzy Logic & Approximate Reasoning Drastic product: Td(a, b) 30

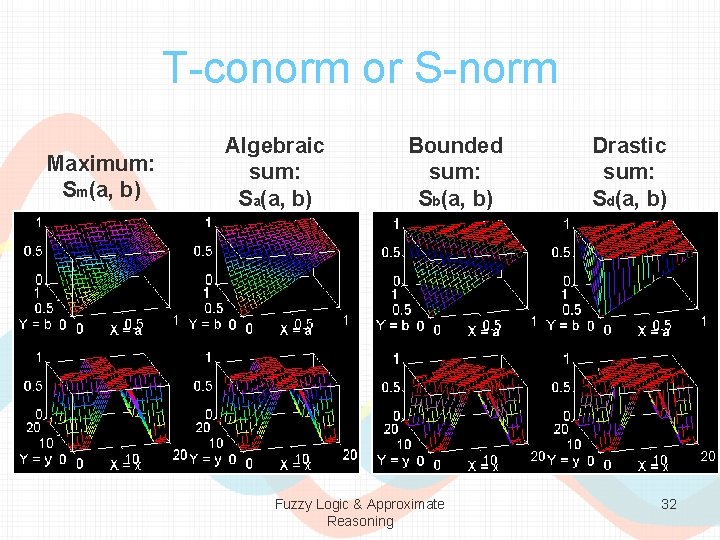
Fuzzy Union: T-conorm or S-norm • Basic requirements: – Boundary: S(1, 1) = 1, S(a, 0) = S(0, a) = a – Monotonicity: S(a, b) < S(c, d) if a < c and b < d – Commutativity: S(a, b) = S(b, a) – Associativity: S(a, S(b, c)) = S(S(a, b), c) • Four examples: – Maximum: Sm(a, b) = max{a, b} – Algebraic sum: Sa(a, b) = a+b-a. b – Bounded sum: Sb(a, b) = min{a+b, 1}. – Drastic sum: Sd(a, b) = Fuzzy Logic & Approximate Reasoning 31

T-conorm or S-norm Maximum: Sm(a, b) Algebraic sum: Sa(a, b) Bounded sum: Sb(a, b) Fuzzy Logic & Approximate Reasoning Drastic sum: Sd(a, b) 32

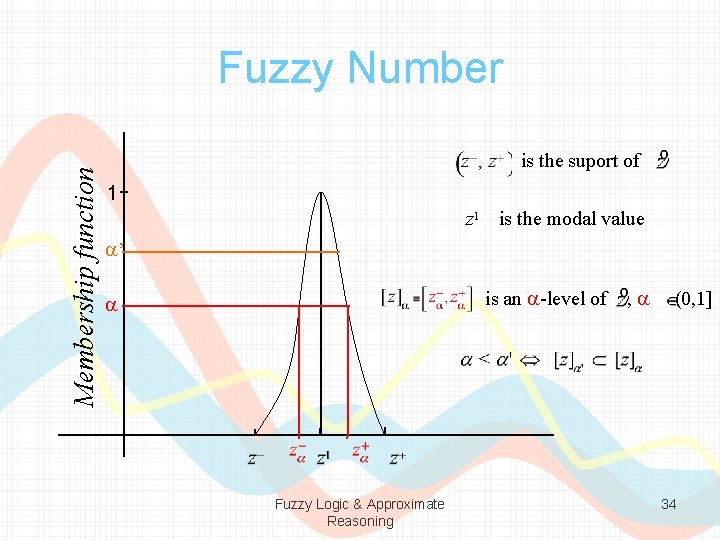
Fuzzy Number • • A fuzzy number A must possess the following three properties: 1. A must be a normal fuzzy set, 2. The alpha levels must be closed for every , 3. The support of A, , must be bounded. Fuzzy Logic & Approximate Reasoning 33

Membership function Fuzzy Number is the suport of 1 z 1 is the modal value a’ is an a-level of a Fuzzy Logic & Approximate Reasoning , a (0, 1] 34

Fuzzy Relations • A fuzzy relation is a 2 D MF: : { ((x, y), (x, y)) | (x, y) X Y} Examples: § x is close to y (x & y are real numbers) § x depends on y (x & y are events) § x and y look alike (x & y are persons or objects) § Let X = Y = IR+ and R(x, y) = “y is much greater than x” The MF of this fuzzy relation can be subjectively defined as: if X = {3, 4, 5} & Y = {3, 4, 5, 6, 7} Fuzzy Logic & Approximate Reasoning 35

Extension Principle The image of a fuzzy set A on X under f(. ) is a fuzzy set B: where yi = f(xi), i = 1 to n If f(. ) is a many-to-one mapping, then Fuzzy Logic & Approximate Reasoning 36

Example – Application of the extension principle to fuzzy sets with discrete universes Let A = 0. 1 / -2+0. 4 / -1+0. 8 / 0+0. 9 / 1+0. 3 / 2 and f(x) = x 2 – 3 Applying the extension principle, we obtain: B = 0. 1 / 1+0. 4 / -2+0. 8 / -3+0. 9 / -2+0. 3 /1 = 0. 8 / -3+(0. 4 V 0. 9) / -2+(0. 1 V 0. 3) / 1 = 0. 8 / -3+0. 9 / -2+0. 3 / 1 where “V” represents the “max” operator, Same reasoning for continuous universes Fuzzy Logic & Approximate Reasoning 37

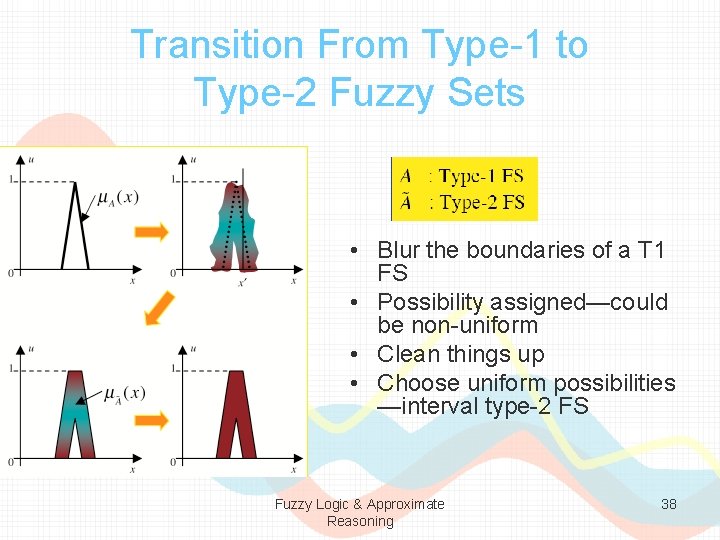
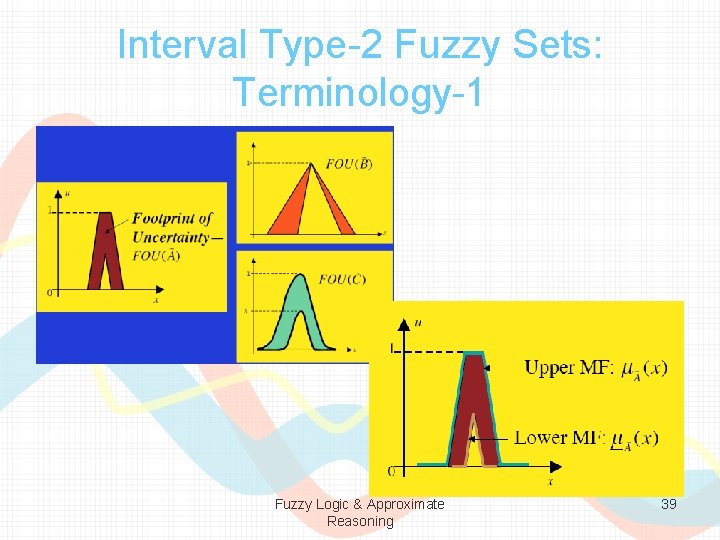
Transition From Type-1 to Type-2 Fuzzy Sets • Blur the boundaries of a T 1 FS • Possibility assigned—could be non-uniform • Clean things up • Choose uniform possibilities —interval type-2 FS Fuzzy Logic & Approximate Reasoning 38

Interval Type-2 Fuzzy Sets: Terminology-1 Fuzzy Logic & Approximate Reasoning 39

Fuzzy Logic & Approximate Reasoning 40

Questions Fuzzy Logic & Approximate Reasoning 41