Fuzzy Logic and Approximate Reasoning 1 Fuzzy Propositions

![Fuzzy Proposition: n n The proposition whose truth value is [0, 1] Classification of Fuzzy Proposition: n n The proposition whose truth value is [0, 1] Classification of](https://slidetodoc.com/presentation_image_h/c78748a82b4d45f0f56a4c4f5307c37b/image-2.jpg)





















- Slides: 25

Fuzzy Logic and Approximate Reasoning 1. Fuzzy Propositions 2. Inference from Conditional Propositions 3. Approximate Reasoning 4. Fuzzy Control
![Fuzzy Proposition n n The proposition whose truth value is 0 1 Classification of Fuzzy Proposition: n n The proposition whose truth value is [0, 1] Classification of](https://slidetodoc.com/presentation_image_h/c78748a82b4d45f0f56a4c4f5307c37b/image-2.jpg)
Fuzzy Proposition: n n The proposition whose truth value is [0, 1] Classification of Fuzzy Proposition Unconditional or Conditional Unqualified of Qualified n Focus on how a proposition can take truth value from fuzzy sets, or membership functions.

Fuzzy Proposition Unconditional and Unqualified n Example:

Unconditional and Qualified Propositions Truth qualified and Probability qualified n Truth qualified “Tina is young is very true” (See Fig. 8. 2)

Unconditional and Qualified Propositions n Probability qualified (See Fig. 8. 3) n Note: Truth quantifiers = “True, False” with hedges Probability quantifiers =“Likely, Unlikely” with hedges

Conditional and Unqualified Propositions Conditional and Unqualified n Example with Lukaseiwicz implication

Conditional and Qualified Propositions Conditional and Qualified

Fuzzy Quantifiers Absolute Quantifiers n Fuzzy Numbers: about 10, much more than 100, at least 5

Fuzzy Quantifiers n Fuzzy Number with Connectives

Fuzzy Quantifiers Relative Quantifier n Example: “almost all”, “about half”, ”most” See Fig. 8. 5

Linguistic Hedges Modifiers n n n “very”, ”more or less”, “fairly”, “extremely” Interpretation Example: Age(John)=26 Young(26)=0. 8 Very Young(26)=0. 64 Fairly Young(26)=0. 89

Inference from Conditional Fuzzy Propositions Crisp Case (See Fig. 8. 6 & Fig. 8. 7)

Inference from Conditional Fuzzy Propositions Fuzzy Case n Compositional Rule of Inference n Modus Ponen

Inference from Conditional Fuzzy Propositions n Modus Tollen n Hypothetical Syllogism

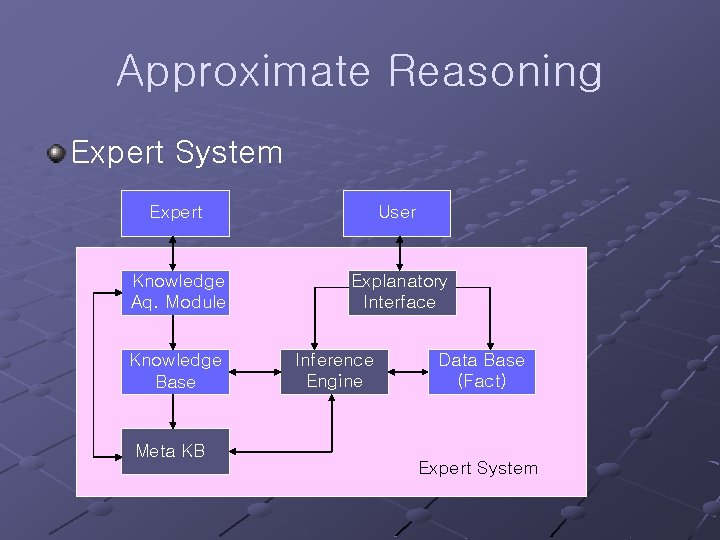
Approximate Reasoning Expert System Expert User Knowledge Aq. Module Explanatory Interface Knowledge Base Meta KB Inference Engine Data Base (Fact) Expert System

Approximate Reasoning Expert System n Knowledge Base (Long-Term Memory) Fuzzy Production Rules (If-Then) n Data Base (Short-Term Memory) Fact from user or Parameters n Inference Engine Data Driven (Forward Chaining, Modus Ponen) Goal Driven (Backward Chaining, Modus Tollen) n n n Meta-Knowledge Base Explanatory Interface Knowledge Acquisition Module

Fuzzy Implications Crisp to fuzzy extension of implication S-Implication from 1

Fuzzy Implications R-Implications from 2 QL-Implication from 3

Selection of Fuzzy Implication Criteria n Modus Ponen n Modus Tollen n Syllogism Some operators satisfies the criteria for 4 kinds of intersection (t-norm) operators

Multi-conditional AR General Schema n Step 1: Calculate degree of consistency

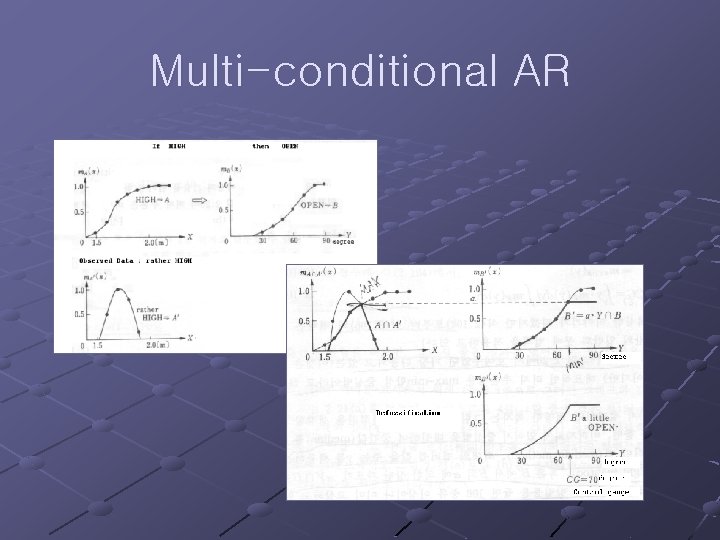
Multi-conditional AR n Step 2: Calculate conclusion Note: Example: HIGH = 0. 1/1. 5 m + 0. 3/1. 6 m + 0. 7/1. 7 m + 0. 8/1. 8 m + 0. 9/1. 9 m + 1. 0/2. 1 m + 1. 0/2. 2 m OPEN = 0. 1/30° + 0. 2/40° + 0. 3/50° + 0. 5/60° + 0. 8/70° + 1. 0/80° + 1. 0/90° (if Completely OPEN is 90°)

Multi-conditional AR Fact: “Current water level is rather HIGH… around 1. 7 m, maybe. ” rather HIGH = 0. 5/1. 6 m + 1. 0/1. 7 m + 0. 8/1. 8 m + 0. 2/1. 9 m If HIGH then OPEN : R(HIGH, OPEN) = A B rather HIGH : A’ = rather HIGH ----------------a little OPEN : B’ = a little OPEN

Multi-conditional AR

Multi-conditional AR Interpretation of rule connection n Disjunctive n Conjunctive n 4 ways of inference

The Role of Fuzzy Relation Equations Role Theorem n n Condition of solution and Solution itself If the condition does not satisfy, approximate solution should be considered.