Fuzzy Sets and Applications l Introduction l Fuzzy

Fuzzy Sets and Applications l Introduction l Fuzzy Sets and Operations

Why fuzzy sets? Types of Uncertainty 1. Randomness : Probability Knowledge about the relative frequency of each event in some domain Lack of knowledge which event will be in next time 2. Incompleteness : Imputation by EM Lack of knowledge or insufficient data 3. Ambiguity : Dempster-Shafer’s Belief Theory => Evidential Reasoning Uncertainty due to the lack of evidence ex) “The criminal is left-handed or not”

Why fuzzy sets? Types of Uncertainty (continued) 4. Imprecision : Ambiguity due to the lack of accuracy of observed data ex) Character Recognition 5. Fuzziness (vagueness) : Uncertainty due to the vagueness of boundary ex) Beautiful woman, Tall man

Why fuzzy sets? Powerful tool for vagueness n n Description of vague linguistic terms and algorithms Operation on vague linguistic terms Reasoning with vague linguistic rules Representation of clusters with vague boundaries

History of Fuzzy Sets and Applications n n n n 1965 Zadeh Fuzzy Sets 1972 Sugeno Fuzzy Integrals 1975 Zadeh Fuzzy Algorithm & Approximate Reasoning 1974 Mamdani Fuzzy Control 1978 North Holland Fuzzy Sets and Systems 1982 Bezdek Fuzzy C-Mean 1987 Korea Fuzzy Temperature Control

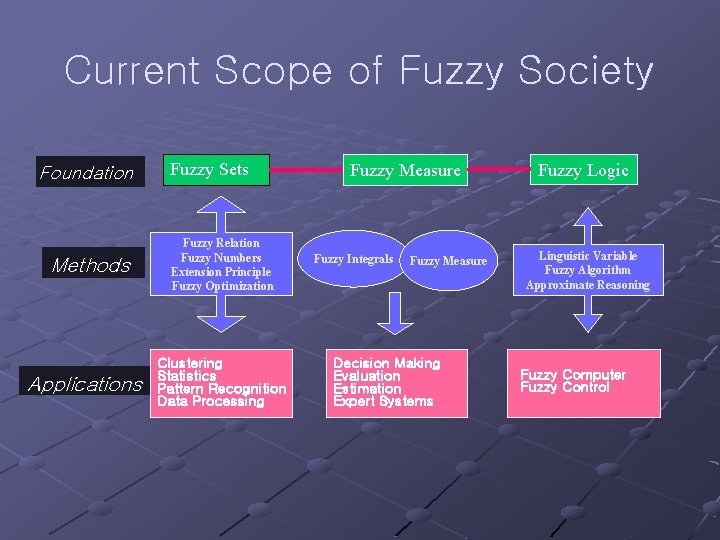
Current Scope of Fuzzy Society Foundation Methods Applications Fuzzy Sets Fuzzy Relation Fuzzy Numbers Extension Principle Fuzzy Optimization Clustering Statistics Pattern Recognition Data Processing Fuzzy Measure Fuzzy Integrals Fuzzy Measure Decision Making Evaluation Estimation Expert Systems Fuzzy Logic Linguistic Variable Fuzzy Algorithm Approximate Reasoning Fuzzy Computer Fuzzy Control

Applications

Topic in the Class • Theory on fuzzy sets 1) fuzzy set 2) fuzzy number 3) fuzzy logic 4) fuzzy relation • Applications 1) fuzzy database 2) fuzzy control and expert system 3) robot 4) fuzzy computer 5) pattern recognition • Rough Sets & Applications

Fuzzy Sets Definition) Fuzzy sunset F on U, the universe of discourse can be represented with the membership grade, F(u) for all u U, which is defined by F : U [0, 1]. Note: 1) The membership function F(u) represents the degree of belongedness of u to the set F. 2) A crisp set is a special case of a fuzzy set, where F : U {0, 1}.

Fuzzy Sets F = {(ui, F(ui) |u i U } = { F(ui) / ui |u i U } = F(ui) / ui F = F(u) / u if U is discrete if U is continuous ex) F = {(a, 0. 5), (b, 0. 7), (c, 0. 1)} ex) F = Real numbers close to 0 F = F(x) / x where F(x) = 1/(1+x 2) ex) F = Real numbers very close to 0 F = F(x) / x where F(x) = {1/(1+x 2)}2

Fuzzy Sets Definition) Support of set F is defined by supp(F) = { u U| F(u) 0} Definition) Height of set F h(F) = Max{ F(u), u U} Definition) Normalized fuzzy set is the fuzzy set with h(F) = 1 Definition) - level set, - cut of F F = {u U| F(u) }

Fuzzy Sets Definition) Convex fuzzy set F: The fuzzy set that satisfies F(u) F(u 1) F(u 2) (u 1 < u 2) u F u 1 u 2 u

Operations Suppose U is the universe of discourse and F, and G are fuzzy sets defined on U. Definition) F = G (Identity) F(u) = G(u) Definition) F G (Subset) F(u) < G(u) Definition) Fuzzy union: F G F G(u) = Max[ F(u), G(u)] = F(u) G(u) Definition) Fuzzy intersection: F G F G(u) = Min[ F(u), G(u)] = F(u) G(u) Definition) Fuzzy complement) FC(~F) Fc(u) = 1 - F(u) u U

Operations Properties of Standard Fuzzy Operators 1) Involution : (Fc)c = F 2) Commutative : F G = G F F G=G F 3) Associativity : F (G H) = (F G) H 4) Distributivity : F (G H) = (F G) (F H) F (G H) = (F G) (F H) 5) Idempotency : F F = F F F=F

Operations 6) Absorption : F (F G) = F F (F G ) = F 7) Absorption by and U : F = , F U = U 8) Identity : F =F F U=F 9) De. Morgan’s Law: (F G) C= FC GC 10) Equivalence : (FC G) (F GC) = (FC GC) (F G) 11) Symmetrical difference: (FC G) (F GC) = (FC GC) (F G)

Operations Note: The two conventional identity do not satisfy in standard operation; Law of contradiction : F FC = Law of excluded middle : F FC = U Other fuzzy operations (1) Disjunctive Sum: F G = (F GC) (FC (2) Set Difference: Simple Difference : F-G = F GC F -G(u) = Min[ F(u), 1 - G(u)] Bounded Difference: F G(u) = Max[0, F(u)- G(u)] G) u U

Operations (3) Bounded Sum: F G(u) = Min[1, F(u) + G(u)] (4) Bounded Product: F G(u) = Max[0, F(u) + G(u)-1] u U (5) Product of Fuzzy Set for Hedge F 2 : F 2 (u) = [ F (u)]2 Fm : Fm (u) = [ F (u)]m (6) Cartesian Product of Fuzzy Sets F 1 F 2 Fn F 1 F 2 Fn(u 1 , u 2, , un) = Min[ F 1(u 1), , , Fn(un) ] ui F i

Generalized Fuzzy Sets Interval-Valued Fuzzy Set of Type 2 L-Fuzzy Set

Generalized Fuzzy Sets Level-2 Fuzzy Set n Ex: “x is close to r” If r is precisely specified, then it can be represented by an ordinary fuzzy set If r is approximately specified, A(B), the fuzzy set A of a fuzzy set B can be used.

Additional Definitions Cardinality of A (Sigma Count of A) n Ex: A =. 1/1 +. 5/2 + 1. /3 +. 5/4 +. 1/6 |A| = 2. 2 Degree of Subsethood S(A, B) Hamming Distance

Decomposition of Fuzzy Sets Decomposition using - level set n Ex:

Additional Notions of Operators Axiomatic Definition of Complement C n Boundary Condition n Monotonicity n Continuity n Involutive

Additional Notions of Operators Some complement operators n Sugeno Class n Yager Class n Note: Parameters can be adjusted to obtain some desired behavior.

Additional Notions of Operators Characterization Theorem of Complement n By strictly increasing function n By strictly decreasing function

Additional Notions of Operators Axiomatic Definition of t-norm i n n n n Boundary Condition Monotonicity Commutative Associative Continuous Subidempotecy Strict Monotonicity

Additional Notions of Operators Some intersection operators n Algebraic Product Bounded Difference Drastic Intersection n Yager’s t-norm n n

Additional Notions of Operators Notes: n n Boundary of t-norm Characterization Theorem t-norm can be generated by a generating function.

Additional Notions of Operators Axiomatic Definition of co-norm u n n n n Boundary Condition Monotonicity Commutative Associative Continuous Subidempotecy Strict Monotonicity

Additional Notions of Operators Some union operators n Algebraic Sum Bounded Sum Drastic Union n Yager’s conorm n n

Additional Notions of Operators Notes: n n Boundary of co-norm Characterization Theorem Co-norm can be generated by a generating function.

Additional Notions of Operators Dual Triples <intersec, union, comp> n Generalized De. Morgan’s Law n Examples

Additional Notions of Operators Aggregation Operators for IF n Compensation (Averaging) Operators h n Example: n n Gamma Model Averaging Operators: Mean, Geometric Mean, Harmonic Mean

Additional Notions of Operators Ordered Weighted Averaging n Definition n Note: Different operations n n n Min -> [1, 0, …, 0], Max -> [0, 0, …, 1] Median -> [0, 0, . . 1, 0, . . 0] Mean -> [1/n, …. 1/n]