Finite Element Lectures for Engineers Dr Ameen Ahmed

Finite Element Lectures for Engineers Dr Ameen Ahmed Nassar Lecture (5)

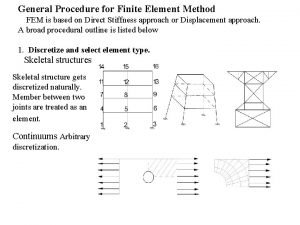
BEAM ELEMENT, HERMITIAN SHAPE FUNCTIONS 1 - Beam-bending theory Consider a long beam, which deforms in the x-y plane due to shear forces (in the y direction) and bending moments (in the z direction), with the x axis being its neutral axis, as shown in the Figure. The conventional Euler-Bernoulli beam bending theory is based upon the following assumptions and approximations: (i) The beam material is homogeneous, isotropic, and linearly elastic; that is, the generalized Hooke's equations are valid for such a case. (ii) The strain components at any point inside the beam are infinitesimal; hence, the Cauchy strain tensor is an acceptable measure for the state of strain within the beam. (iii) The variation of the lateral deflection across the beam thickness is negligible. (iv) Transverse normal stress is negligible. 2

Considering the continuous beam shown in the Figure, with forces and moments bending the beam in the x-y plane, it is clear that the displacement component in the z direction (w) is negligible, and it can also be deduced from the previous assumptions that the displacement component in the y direction (the lateral deflection v) can be approximated at any point (x, y, z) inside the beam, as a function of x only. 3

2 - Hermitian interpolation Consider a two-node element, where the lateral displacements and slopes at its nodes are defined as shown in the Figure. It is required to find an interpolation expression for v(x) in terms of v and θ. 4

Substituting from and rearranging the terms, it can be shown that: 5

6

3 - Derivation of stiffness matrix for two-node beam element Considering a two-node beam element, shown before, the element stiffness matrix can be derived using an algorithm similar to that described before. The steps of the derivation procedure are summarized in this section. 7

8

9

10

11

12

Example Use the finite element procedure to find the maximum deflection and end reactions for a beam with fixed ends as shown in the Figure, where 13

The beam can be divided into two beam elements of equal length, as shown in the Figure, where nodes 1, 2, and 3 are assumed at points a, b, and c, respectively. 14

15

which is the maximum deflection of the beam, and the values of all the six components of the nodal displacement vector of the beam are now known. Substituting in the assembled matrix equation of the beam, then the values of the end reactions can be obtained as follows: 16

4 - Equivalent nodal loading Consider first a two-node beam element subjected to a concentrated shear force F, acting at point f, as shown in the Figure. The lateral deflection v at any point on the beam axis is as given before. At point f, it can be deduced from the Figure that: 17

Hence from the above Equations, it is clear that the equivalent nodal shear forces and moments which will do the same work done by the actual force are, as follows: 18

Consider next a two-node beam element under a uniformly distributed loading with intensity q, as shown in the Figure. The force acting on an infinitesimal length Δx of the beam axis is: 19

Comparing the previous equations, then the components of the equivalent loading vector can be obtained as follows: Consider a beam with fixed ends, which is modelled by a single two-node element, as shown in the Figure. Let Feq represent the equivalent loading vector, and R be the vector of reactions at the fixed ends. The nodal displacement vector of the element can be written for such case as follows: 20

21