Finite Element Lectures for Engineers Dr Ameen Ahmed










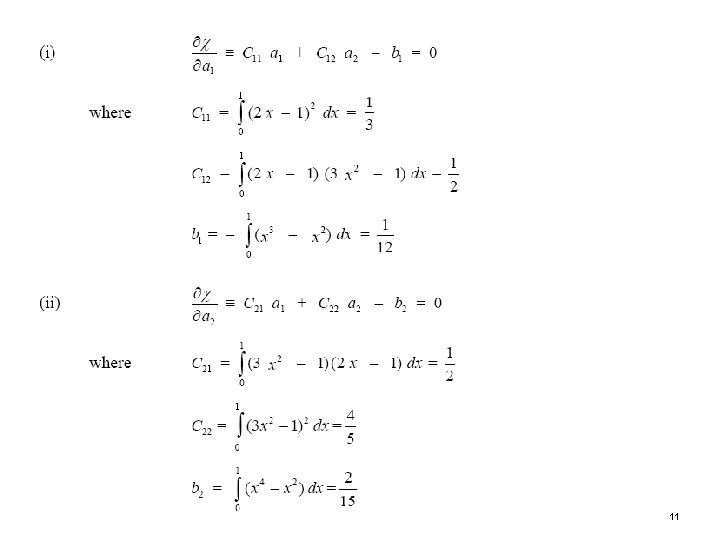


















- Slides: 30

Finite Element Lectures for Engineers Dr Ameen Ahmed Nassar Lecture (1)

VARIATIONAL APPROACH Introduction • For the case of one-dimensional problems, a variational statement is generally expressed as follows: 2

In 1870, Rayleigh presented a direct method for the solution of variational problems, and Ritz refined and extended Rayleigh's method in 1909 (see Zienkiewicz 1977). The Rayleigh-Ritz method can also be used for the solution of a differential equation, provided that an equivalent variational statement is available. 3

Steps of Rayleigh-Ritz Method 4

Step 1: Assume a Trail Function Solution • Such a solution is usually expressed in terms of unknown parameters and basis function terms, in the following form: where αj represents the unknown coefficients, and ψj is a given sequence of a linearly independent function (the basis function). • The basis function can be a Trigonometric series, Legendre polynomials, etc. The simplest choice is the Algebraic series: 5

Step 2: Verify the Boundary Conditions The given boundary conditions (say l conditions) are to be substituted into the previous solution and l coefficients are to be eliminated, reducing the solution to the following form Where n=m-l. 6

For the given example: 7

Step 3: Substitution of the Solution In this step, the assumed solution which satisfies the given boundary conditions is substituted in the variational expression, and the variational functional is reduced to a function in terms of the unknown coefficients, i. e. 8

Step 4: Minimize the Variational Functional The mathematical condition for the functional χ to be an extremum (maximum, minimum, or stationary) is: 9

Step 5: Solution of the Resulting Equations 10
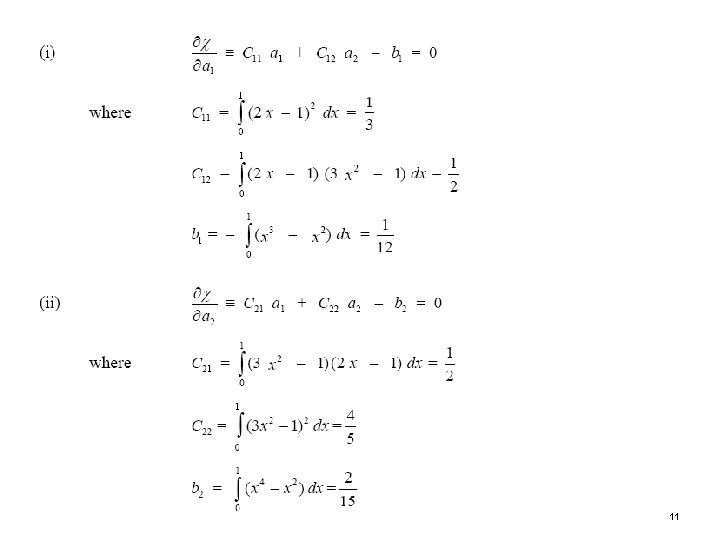
11

12

Example: 13

14

STRESS ANALYSIS USING THE VARIATIONAL APPROACH Due to the symmetry of stress and strain matrices, an engineering representation is usually adopted in terms of the following stress and strain vectors: For the case of infinitesimal strain, the components of the strain matrix are defined in terms of displacement components by means of the following equations: 15

For an isotropic, homogeneous, linearly elastic material, the strain components can be related to the stress components, at the same point inside the material, by generalized Hooke's equations which are: Hence, the components of the stress matrix may be expressed in terms of the components of the strain matrix, as follows: 16

The Minimum Potential Energy Theorem The total potential energy of a structure under mechanical loading, can be expressed as follows where W is the work done by the applied forces and U is the strain energy of the structure defined as follows: The minimum total potential energy states that; the exact solution of a structural problem is the one, from all compatible displacement fields, which makes the totalpotential energy of the structure a minimum. 17

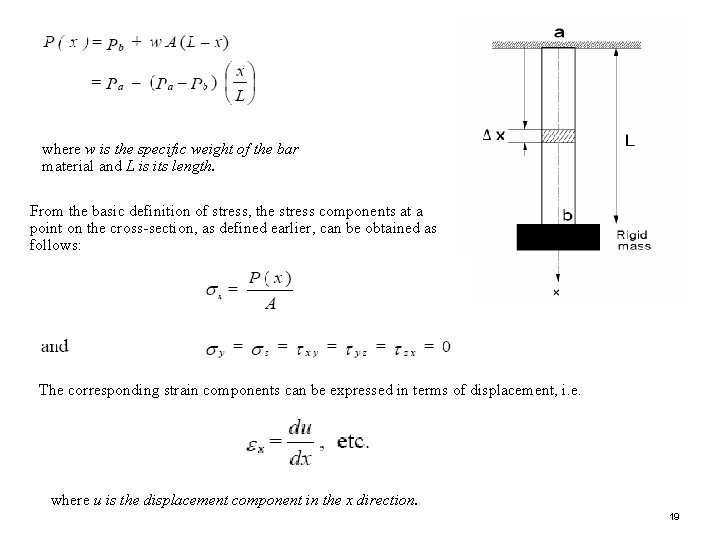
The Principles of Virtual Work If variations in the strain energy and work done by the applied forces are caused by an infinitesimal virtual deformation, then it can be deduced from the previous theorem that: and this proves the principle of virtual work, which states that; during a virtual deformation of an engineering component, the work done by the applied forces is equal to the change in its internal energy. One-dimensional example Consider a heavy bar which is hung vertically from one end a and carries a rigid mass at the other end b, as shown in the Figure below. The bar is subjected to a thrust force Pb acting at the free end b due to the weight of the rigid mass, and the thrust force at the fixed end a, is equal to the total weight of the bar and the rigid mass. If the bar has a uniform cross-sectional area A, then it can be deduced that: 18

where w is the specific weight of the bar material and L is its length. From the basic definition of stress, the stress components at a point on the cross-section, as defined earlier, can be obtained as follows: The corresponding strain components can be expressed in terms of displacement, i. e. where u is the displacement component in the x direction. 19

Using the generalized Hooke's equations, the strain components can be expressed as follows: Hence, it can be shown that: which represents the governing differential equation for the bar problem. The total strain energy of the bar can, therefore, be expressed as follows: 20

The total work done by the thrust force during bar deformation can be written in the following form: Hence, the total potential energy of the bar can be expressed in terms of the bar displacement, as follows: 21

Hence, the total potential energy of the problem, can be expressed in terms of the trialfunction solution as follows: 22

23

24

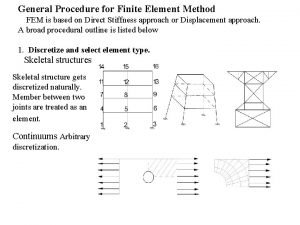
DISCRETIZATION CONCEPTS Pointwise discretization An attempt will be shown here for the derivation of such an interpolation expression, and for simplicity the nodal coordinates considered are: Substituting the three values of u into the algebraic expression of u(x), it can be deduced that: 25

and can be modified as follows: 26

then the previous equation of displacement may be rewritten in the following simplified form: The steps of the Rayleigh-Ritz procedure, for the bar example, based upon the Point-wise discretized solution , can be summarized as follows: 27

28

29

30
 Ahmed muhudiin ahmed
Ahmed muhudiin ahmed Ameen rihani
Ameen rihani Definition of amen
Definition of amen Learning objectives of non finite verbs
Learning objectives of non finite verbs Finite and nonfinite verbs examples
Finite and nonfinite verbs examples Fused relative clause
Fused relative clause Finite and non finite
Finite and non finite Learning objectives for finite and non finite verbs
Learning objectives for finite and non finite verbs Finite element method example
Finite element method example Finite element method
Finite element method Image preprocessing
Image preprocessing Finite elements method
Finite elements method Hourglass modes finite element method
Hourglass modes finite element method Finite element methods
Finite element methods Finite element
Finite element Finite element method
Finite element method Cst finite element
Cst finite element Finite element method
Finite element method Introduction to fem
Introduction to fem Finite element analysis
Finite element analysis Finite element method
Finite element method Truss finite element analysis
Truss finite element analysis Fem geotechnics
Fem geotechnics Signal element vs data element
Signal element vs data element Distinguish between a signal element and a data element.
Distinguish between a signal element and a data element. Ludic space
Ludic space Comsats virtual campus lectures
Comsats virtual campus lectures Data mining lectures
Data mining lectures Reinforcement learning lectures
Reinforcement learning lectures Theory of translation lectures
Theory of translation lectures Cs106b lectures
Cs106b lectures