Finite Element Lectures for Engineers Dr Ameen Ahmed

Finite Element Lectures for Engineers Dr Ameen Ahmed Nassar Lecture (2)

WEIGHTED-RESIDUAL APPROACH The governing equations of many engineering boundary value problems, are usually expressed in terms of ordinary or partial differential equations, and it is advantageous to find a mathematical procedure which can be employed for the derivation of equivalent integral equations or variational statements. The weighted-residual approach , which can deal with differential equations directly, can easily be used for such derivations which are essential for the finite element implementation. Consider a one-dimensional boundary value problem governed by a linear ordinary differential equation expressed generally as follows: within a domain L, together with R boundary conditions, where: 2

The weighted-residual theorem for this class of problems can be stated as follows: Let ~y (x) be an assumed solution which satisfies the given boundary conditions. Then, the necessary and sufficient condition for ~y (x) to be an exact solution to the above Equation is for arbitrary weighting functions W(x). An algorithm for the derivation of approximate solutions to one-dimensional problems described earlier, based upon the previous theorem, can be summarized in terms of the following steps: 3

Given an R boundary conditions, they should be substituted into the above assumed solution, and R coefficients may be eliminated, reducing the trial function to: where n = m-R, a 1, a 2, . . . , an are unknown parameters. 4

Since the above Equation may not represent an exact solution, then the substitution will generally lead to an error or residual function defined as follows: An accurate solution is the one which minimizes R and its weighted average over the problem domain, i. e. with appropriate weighting functions Wi(x). If n different weighting functions are selected, then a system of n simultaneous algebraic equations in a 1, a 2, . . . , an may be obtained. 5

There are many criteria for the definition of weighting functions, and the widely used ones will be illustrated with the aid of a simple example, similar to that employed in before; that is, the following differential equation will be considered: 1 - Point-collocation method 6

7

8

Stress Analysis Using Weighted Residual Method Consider a cantilever beam under a uniformly distributed load with intensity q (force per unit length), as shown in the Figure. The governing equation of the lateral deflection of the beam, v(x), is: 9

10

2 - Least-squares method 11

12

Taking the limits, the previous summation becomes mathematically equivalent to: Considering the example defined before, if three points are selected, such that: 13

14

Alternatively, using the integrated least-squares method, the following two equations are obtained : Engineering Example: Consider a simply supported beam under a uniformly distributed load with intensity q. The bending moment in this case is: 15

and the governing differential equation is similar to that given in the previous example, with the following boundary conditions: 16

17

18

3 - Galerkin method 19

Considering the example given before, a trial-function solution which satisfies the given boundary conditions can be expressed as follows: 20

21

22

Basic Steps Of Finite Element Method The procedure of the finite element method applied to one-dimensional problems will be discussed within the simple example of the bar problem described earlier. Derivation of the two-node bar finite element Consider a subdomain or a finite element defined as the part between points or nodes, i and j, on the bar. The element equations can be derived by applying the steps of the discretized Rayleigh-Ritz method. 23

24

The boundary conditions may be substituted in the assumed solution, however, for a general derivation of finite element equations, it is recommended to consider the boundary conditions after the assembly of the equations for the whole domain, as will be explained later. 25

26

27

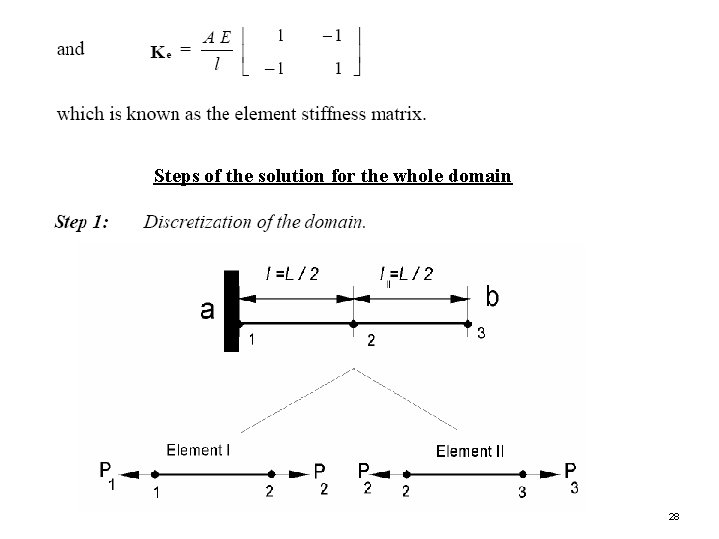
Steps of the solution for the whole domain 28

The domain of the bar problem is divided into two subdomains, and each subdomain can be considered a two-node bar element, as shown above. Notice that, the actual thrust forces at the specified nodes are as follows: Using the element derivation given before, the matrix equation of the first element can be written explicitly as follows: 29

30

31

32

Example: Consider a stepped bar fixed at one end and subjected to an axial force F at the other end. Using two node bar elements with the discretized domain shown in the Figure, find the axial displacement at the free end. The bar is divided into two elements, the matrix equation of each can be deduced such that, for the first element: 33

34