Finann matematika ROKOVN vitel BANKA dlunk vitel BANKA

Finanční matematika ÚROKOVÁNÍ
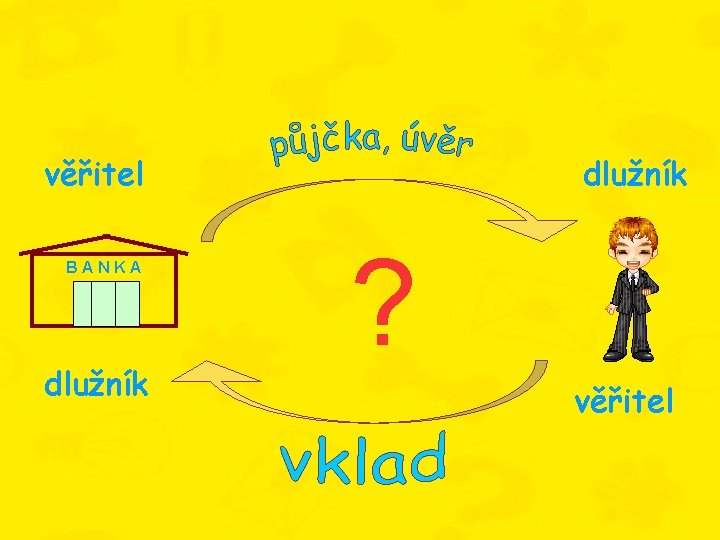
věřitel BANKA dlužník ? věřitel
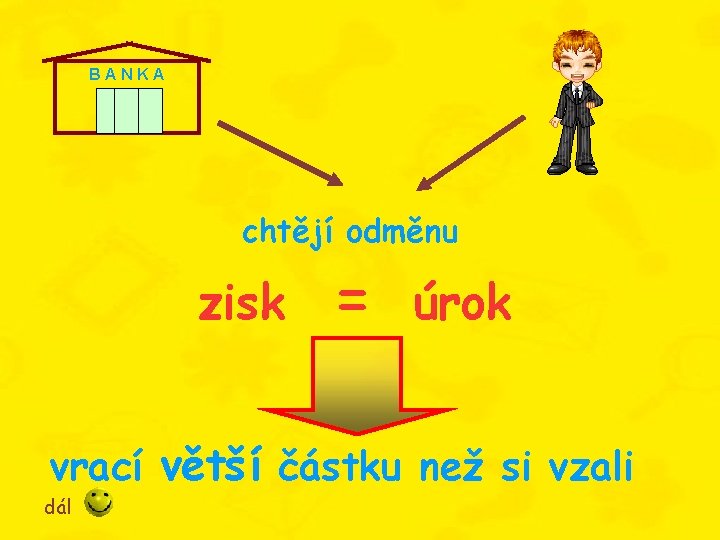
BANKA chtějí odměnu zisk = úrok vrací větší částku než si vzali dál

• Poskytne-li věřitel dlužníkovi na určitou dobu nějakou peněžní částku (vklad klienta do banky, půjčka banky klientovi), požaduje nazpět částku, která je větší než byla půjčena. dál

Základní pojmy: jistina úroková míra úrokové období dál
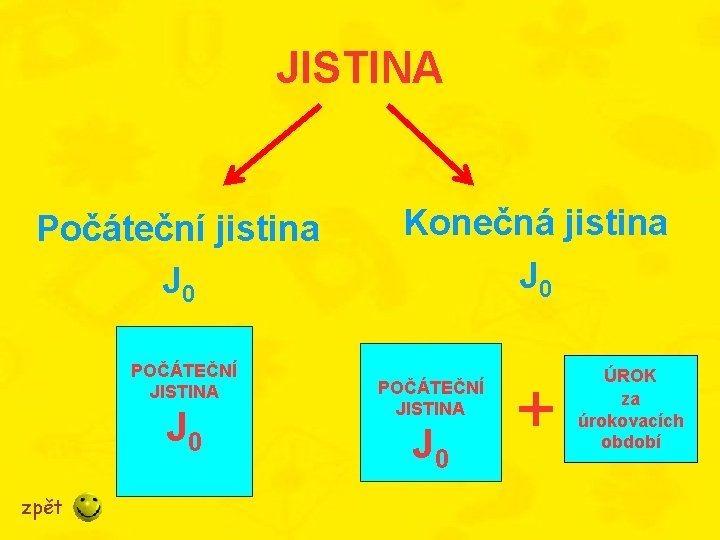
JISTINA Počáteční jistina J 0 POČÁTEČNÍ JISTINA J 0 zpět Konečná jistina J 0 POČÁTEČNÍ JISTINA J 0 + ÚROK za úrokovacích období

POČÁTEČNÍ JISTINA • označujeme J 0 • původní částka peněz, která se půjčuje nebo byla vložena (tzv. počáteční kapitál – vklad) POČÁTEČNÍ JISTINA J 0 zpět
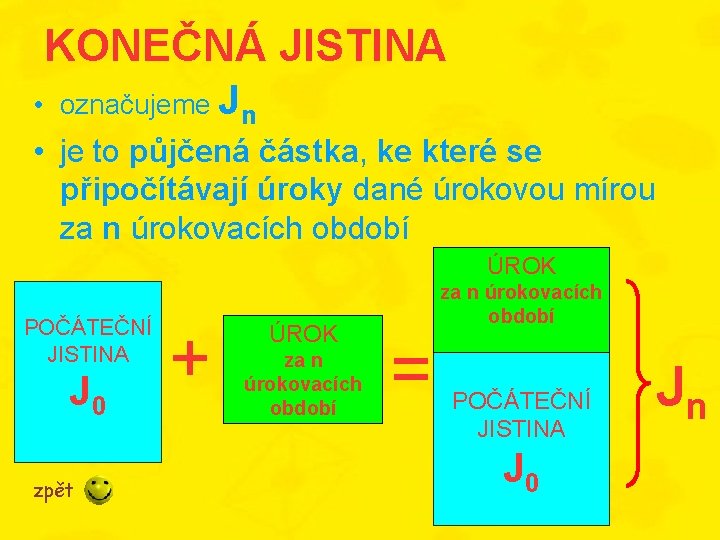
KONEČNÁ JISTINA • označujeme Jn • je to půjčená částka, ke které se připočítávají úroky dané úrokovou mírou za n úrokovacích období ÚROK POČÁTEČNÍ JISTINA J 0 zpět + ÚROK za n úrokovacích období = POČÁTEČNÍ JISTINA J 0 Jn

ÚROK • je peněžní částka, kterou klient zaplatí věřiteli, za půjčení peněz • rozumíme částku, o kterou splatná částka převyšuje základ (jistinu) vkladu či půjčky ÚROK JISTINA dál odměna za půjčení peněz půjčená částka

ÚROK » označujeme U • úrok je určen: – velikostí úrokové míry – jistinou – úrokovým obdobím zpět

ÚROKOVÉ OBDOBÍ » označujeme t • je to doba, během které se musí splatit dlužná částka a úroky • doba, během které se vklad nebo půjčené peníze úročí dál ů c í s ě 12 m 16, 5 30 m ěsíc ů roků 22 l et 27 dnů

Pro výpočet úrokového období se používají 2 základní metody: Anglická obchodní metoda Německá obchodní metoda „ 30/360“ - vychází z přesného - zjednodušuje počet dní počtu dní - každý měsíc má 30 dnů - včetně přestupného rok má 360 dní roku ukázka
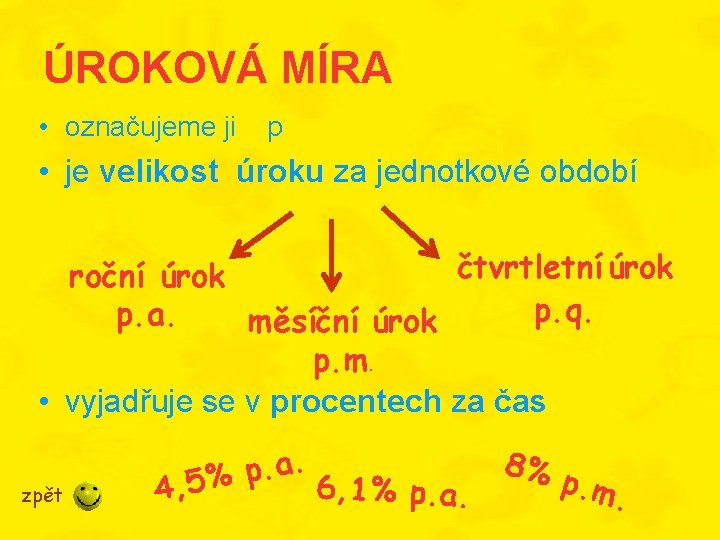
ÚROKOVÁ MÍRA • označujeme ji p • je velikost úroku za jednotkové období čtvrtletní úrok roční úrok p. q. p. a. měsíční úrok p. m. • vyjadřuje se v procentech za čas zpět . a. p 6, 1% p. a. 4, 5% 8% p. m .

Výpočet úrokového období pomocí 30/360 Př. : Peníze byly půjčené od 13. 5. – 16. 9. 1) Metoda číselné osy 3) Metoda podle vzorce t = 30(m 2 – m 1) + (d 2 – d 1) příklady 2) Odčítací metoda 16. 9. - 13. 5. 3 + 4 * 30 = =123 dní
Vypočítejte: Peníze b y od 23. 5 Peníze byly půjčené . 2006 – od 1. 1. 2006 – 1. 4. 2006. né e č j ů p y l y 6. b 0 e 0 z 2 í. n 10 Pe. 1 – 02 0 2. 7. od 18 od 28. 11. 2000 – 1. 4. 2012. zpět né 8. 11. 20 06. Peníze byly půjčené od 14. 10. 2003 – 13. 1. 2006. Peníze jsou půjčené ly půjče od 2. 9 byly p . 2002 ůjčené – 13. 7 . 2006.

Druhy úrokování jednoduché konec složené

Jednoduché úrokování – úrok se za stejné úrokovací doby nemění – počítá se stále z téže původní jistiny J 0 – úrok je lineární funkcí času dál
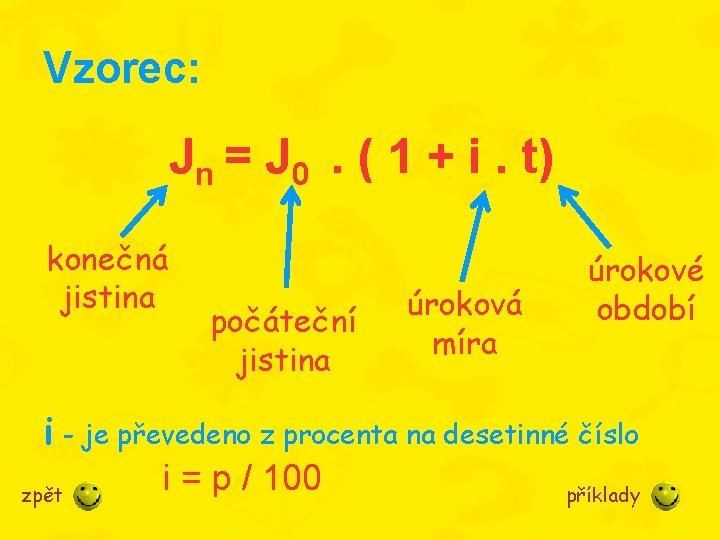
Vzorec: Jn = J 0. ( 1 + i. t) konečná jistina počáteční jistina úroková míra úrokové období i - je převedeno z procenta na desetinné číslo i = p / 100 zpět příklady

Vypočtěte: Na jakou částku vzroste Kč 7 500, - za 8 let při 12% p. a. ? Na jakou částku by vzrostla Kč 1, - za 200 let při 10% p. a. ? Za jak dlouho vzroste jistina Kč 75 000, - na Kč 222 860, - při 9, 5% p. a. ? Jak vysokou částku musíme uložit, aby nám za 9 let vzrostla při 13% p. a. na Kč 100 000, -? Jakou částku musíme dnes uložit při 8% p. a. , aby nám vzrostla za 10 let na Kč 150 000, -? KONTROLA zpět

Složené úrokování – na konci každého úrokovacího období se připíše k předešlé jistině (konečná jistina) úrok za plynulé období – v příštím úrokovacím období se pak nový úrok počítá z počáteční jistin a připsaných úroků z předešlých období dál
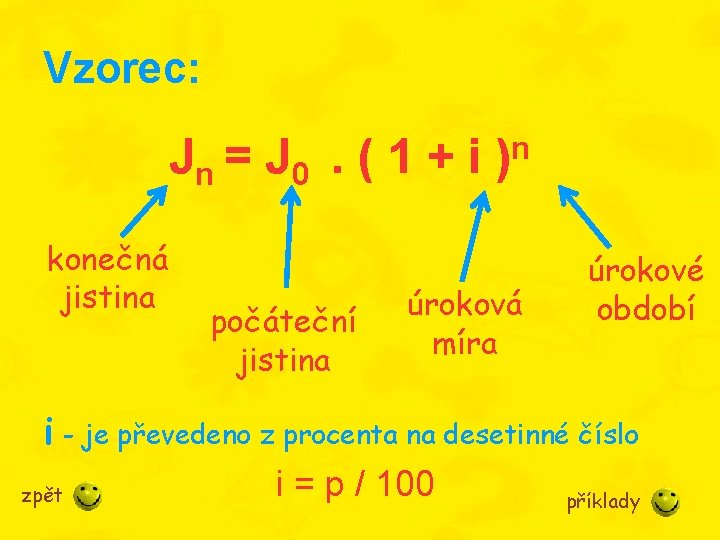
Vzorec: Jn = J 0. ( 1 + i konečná jistina počáteční jistina n ) úroková míra úrokové období i - je převedeno z procenta na desetinné číslo i = p / 100 zpět příklady

Příklad 1. Zadání: Paní Opatrná uložila na konci roku do banky 16 800 Kč na termínový vklad na 4 roky s úrokovou mírou 5. 1%. Úrokuje se jednou za rok. Kolik korun bude paní Opatrné v den splatnosti vkladu vyplaceno? jn = j 0. ( 1+ )n Jn = 19 908, 10 Kč jn = 16 800. ( )4 jn = 16 800. ( 1+ 0, 04335 )4 jn = 16 800. ( 1, 04335 )4 jn = 16 800. 1, 185 Paní Opatrné bude vyplaceno 19 908, 10 Kč.

Příklad 2. Pan Skrblík si založil na začátku roku vkladní knížku a uložili na ni 17 300 Kč. Banka úročí vždy na konci každého pololetí, používá složené úročení. Kolik korun obdržel pan Skrblík od banky po dvou letech za předpokladu, že úroková míra byla po celou dobu neměnná a činila 1, 9%. Výpočet: Jn 2 =17 300( 1+ Jn 2 =17 300× 1, 016152 Jn 2=17863, 3 Pan Skrblík obdržel přibližně 17 863 Kč. )2

Příklad 3. Paní Lakotná uložila dne 26. 6. částku 180 000 Kč na termínovaný účet na tři měsíce s revolvingem. Banka zaručuje dlouhodobě neměnnou roční úrokovou míru 1, 9%. Úrokovací období jsou 3 měsíce, užívá se standart 30 A/360. Úrok je klientce připisován na běžný účet na konci každého tříměsíčního období. Kolik Kč připsala dohromady banka na běžný účet, byl-li vklad úročen sedmkrát? Řešení: Jo=180 000 T=3 měsíce p=1, 9% U= U= U= Banka připsala na běžný účet 5087, 25 Kč

Příklad 4. Začátkem roku jsme uložily na vkladní knížku 135 000 Kč. Banka úročí vklad s úrokovou mírou 2, 3% jednou ročně, vždy na začátku následujícího roku, užívá standart 30 A/360; úrok převádí na náš běžný účet. Kolik korun činí úrok po zdanění za tři roky? Jo=135 000 Kč p=2, 3% t=3 roky u=jo. p =135 000. 2, 3 = 3105 100 Uz=2639, 25 Kč. 3 Uz=7917, 75 Kč Úrok činí po zdanění 7917, 75 Kč.

Vypočtěte: Na jakou částku vzroste Kč 9 500, - za 9 let při 8% p. a. ? Na jakou částku by vzrostla Kč 1, - za 50 let při 13% p. a. ? Jakou částku musíme dnes uložit při 6% p. a. , aby nám vzrostla za 20 let na Kč 150 000, -? Jak vysokou částku musíme uložit, aby nám za 11 let vzrostla při 9% p. a. na Kč 100 000, -? Za jak dlouho vzroste jistina Kč 75 000, - na Kč 222 860, - při 8% p. a. ? KONTROLA zpět



Prezentaci vypracovali žáci devátého ročníku: Petra Valentová Vendula Skalová Eliška Dostálková Aneta Barešová Zdeněk Dušek Jaroslav Bareš a Zuzana Kropáčková Dne 22. 5. 2009

Konec
- Slides: 30






















































