Exploiting TreeDecomposition in Search The ANDOR Paradigm Rina

Exploiting Tree-Decomposition in Search: The AND/OR Paradigm Rina Dechter Bren School of ICS University of California, Irvine Collaborators: Kalev Kask Radu Marinescu Robert Mateescu Vibhav Gogate Vienna, Dec 2004 Caltech, December 1 st

Outline n n Background: Search and inference in Graphical models AND/OR search trees n n AND/OR search graphs n n Pseudo spanning trees, dfs trees Tree-width and path-width bounds Relationship to algorithmic and compilation schemes. Vienna, Dec 2004

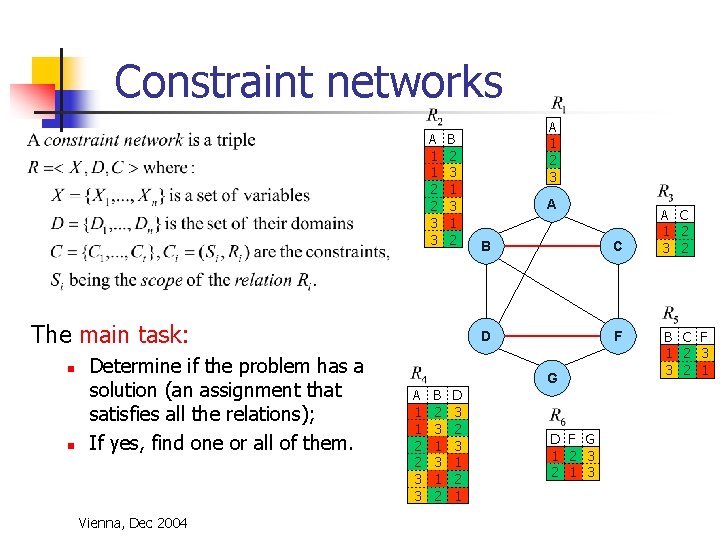
Constraint networks A 1 1 2 2 3 3 B 2 3 1 2 The main task: n n Determine if the problem has a solution (an assignment that satisfies all the relations); If yes, find one or all of them. Vienna, Dec 2004 A 1 2 3 A B C D F G A 1 1 2 2 3 3 B 2 3 1 2 D 3 2 3 1 2 1 D F G 1 2 3 2 1 3 A C 1 2 3 2 B C F 1 2 3 3 2 1

Probabilistic Networks Smoking P(S) P(C|S) P(B|S) lung Cancer Bronchitis P(X|C, S) X-ray P(D|C, B) Dyspnoea CPD: C 0 0 1 1 B D=0 D=1 0 0. 1 0. 9 1 0. 7 0. 3 0 0. 8 0. 2 1 0. 9 0. 1 P(S, C, B, X, D) = P(S) P(C|S) P(B|S) P(X|C, S) P(D|C, B) P(S|d)= ? MPE: argmax P(S) P(C|S) P(B|S) P(X|C, S) P(D|C, B) Vienna, Dec 2004

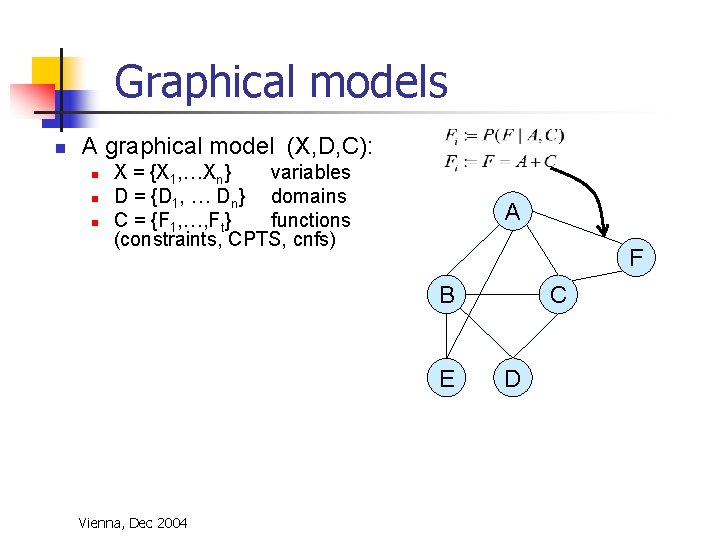
Graphical models n A graphical model (X, D, C): n n n X = {X 1, …Xn} variables D = {D 1, … Dn} domains C = {F 1, …, Ft} functions (constraints, CPTS, cnfs) A F B E Vienna, Dec 2004 C D

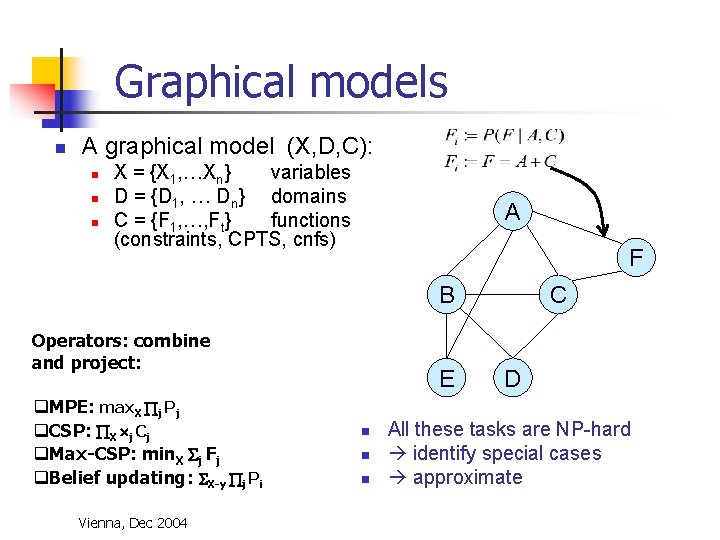
Graphical models n A graphical model (X, D, C): n n n X = {X 1, …Xn} variables D = {D 1, … Dn} domains C = {F 1, …, Ft} functions (constraints, CPTS, cnfs) A F B Operators: combine and project: q. MPE: max. X j Pj q. CSP: X j Cj q. Max-CSP: min. X j Fj q. Belief updating: X-y j Pi Vienna, Dec 2004 E n n n C D All these tasks are NP-hard identify special cases approximate

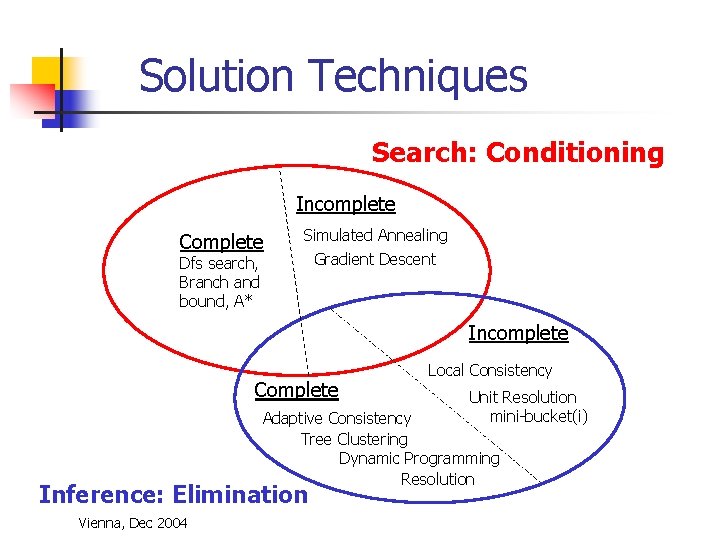
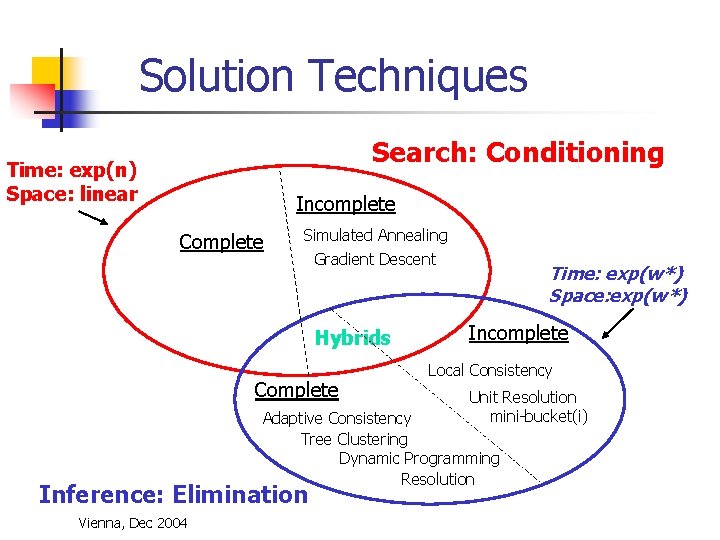
Solution Techniques Search: Conditioning Incomplete Complete Simulated Annealing Dfs search, Branch and bound, A* Gradient Descent Incomplete Complete Local Consistency Unit Resolution mini-bucket(i) Adaptive Consistency Tree Clustering Dynamic Programming Resolution Inference: Elimination Vienna, Dec 2004

Solution Techniques Search: Conditioning Time: exp(n) Space: linear Incomplete Complete Simulated Annealing Gradient Descent Hybrids Complete Time: exp(w*) Space: exp(w*) Incomplete Local Consistency Unit Resolution mini-bucket(i) Adaptive Consistency Tree Clustering Dynamic Programming Resolution Inference: Elimination Vienna, Dec 2004

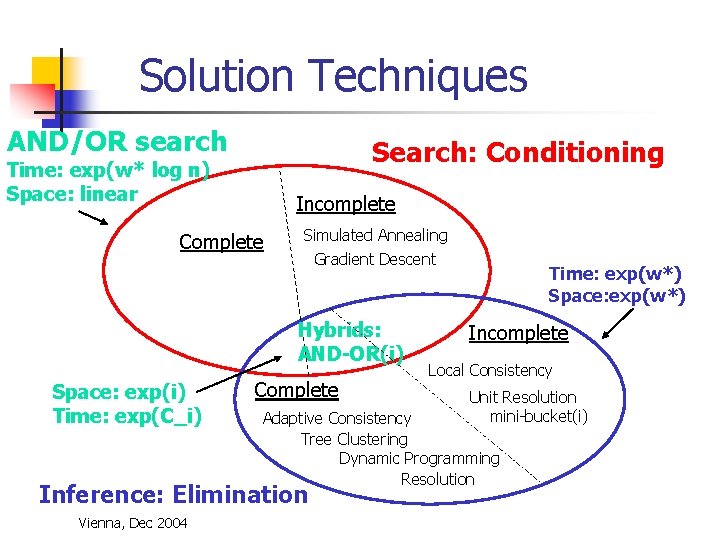
Solution Techniques AND/OR search Search: Conditioning Time: exp(w* log n) Space: linear Incomplete Complete Simulated Annealing Gradient Descent Hybrids: AND-OR(i) Space: exp(i) Time: exp(C_i) Complete Incomplete Local Consistency Unit Resolution mini-bucket(i) Adaptive Consistency Tree Clustering Dynamic Programming Resolution Inference: Elimination Vienna, Dec 2004 Time: exp(w*) Space: exp(w*)

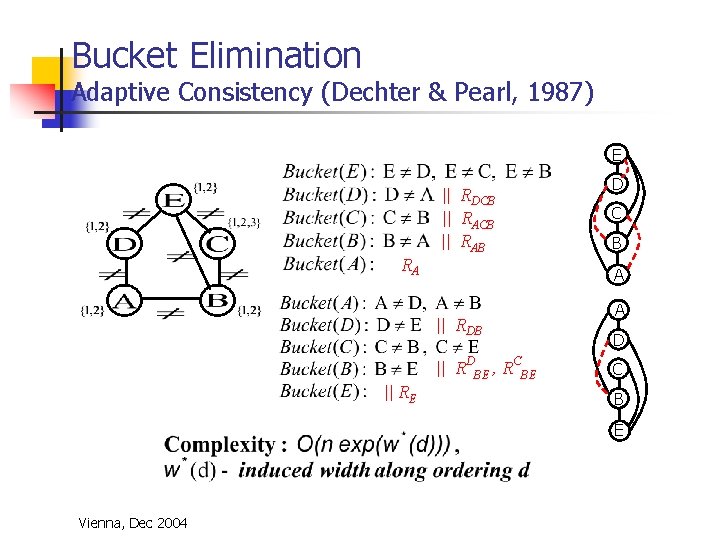
Bucket Elimination Adaptive Consistency (Dechter & Pearl, 1987) E || RDCB || RAB RA C B A || RDBE , RCBE || RE D A D C B E Vienna, Dec 2004

Outline n n Background: Search and inference in Graphical models AND/OR search trees n n AND/OR search graphs n n Pseudo spanning trees, dfs trees Tree-width and path-width bounds Relationship to algorithmic and compilation schemes. Vienna, Dec 2004

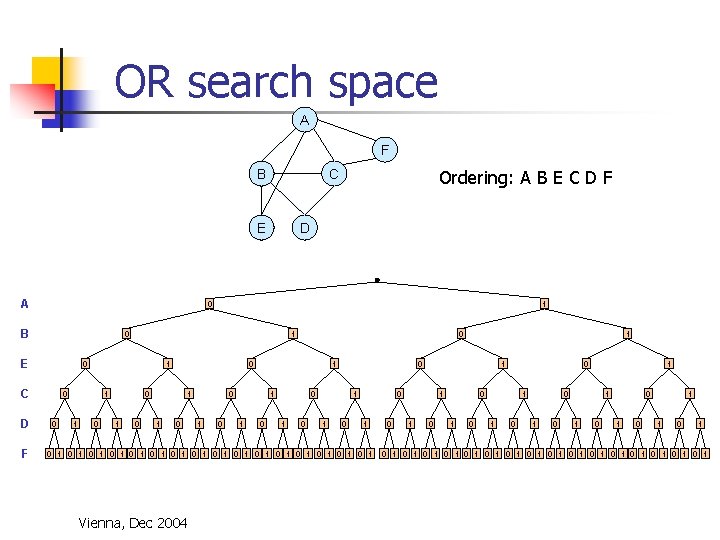
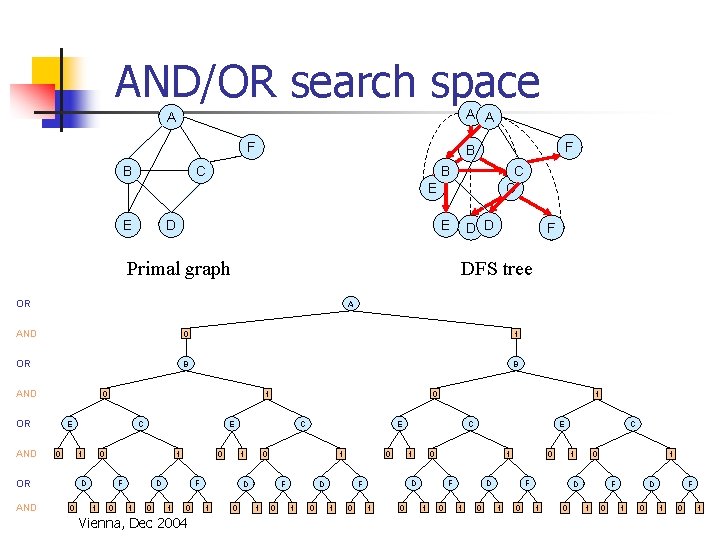
OR search space A F B E A 1 0 E 1 0 C F D 0 B D Ordering: A B E C D F C 1 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 0 1 0 1 0 1 Vienna, Dec 2004 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 1

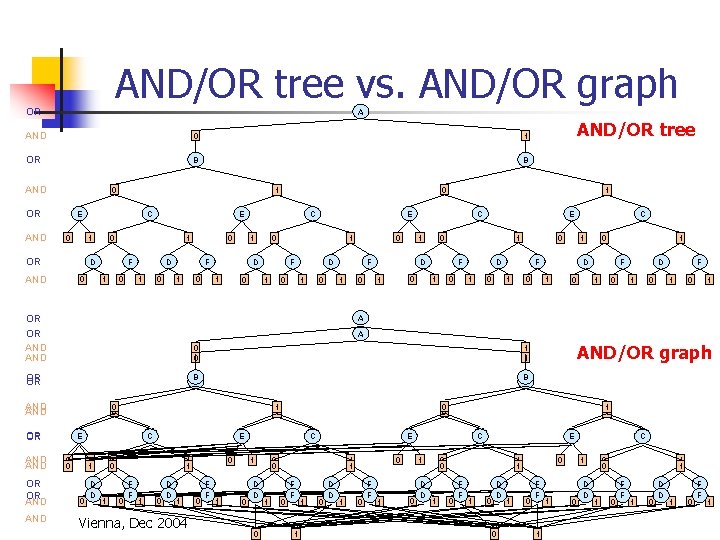
AND/OR search space A A A F B C B C C E E D E Primal graph D D F DFS tree OR A AND 0 1 OR B B AND 0 OR AND E 0 OR AND C 1 E 0 1 D 0 F 1 0 0 D 1 0 F 1 0 Vienna, Dec 2004 0 0 F 1 0 1 D 1 E C 1 0 D 1 1 0 1 0 E 0 1 D F 1 C F 1 0 0 D 1 0 1 F 1 0 C 0 1 D 1 0 F 1 0 1

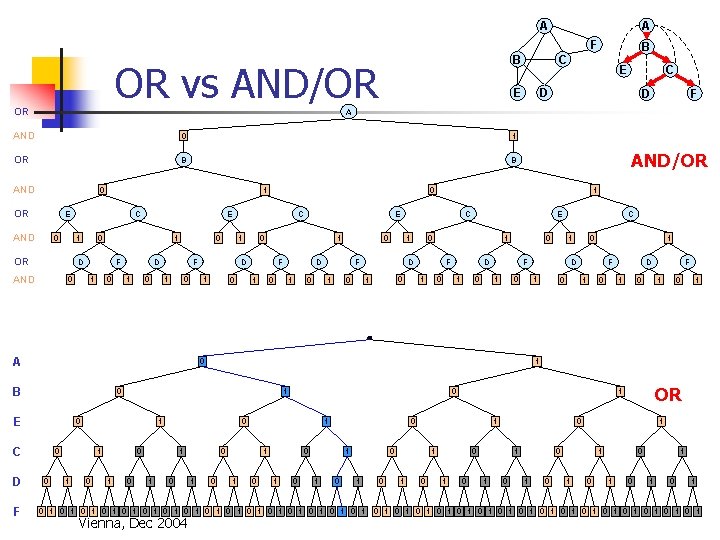
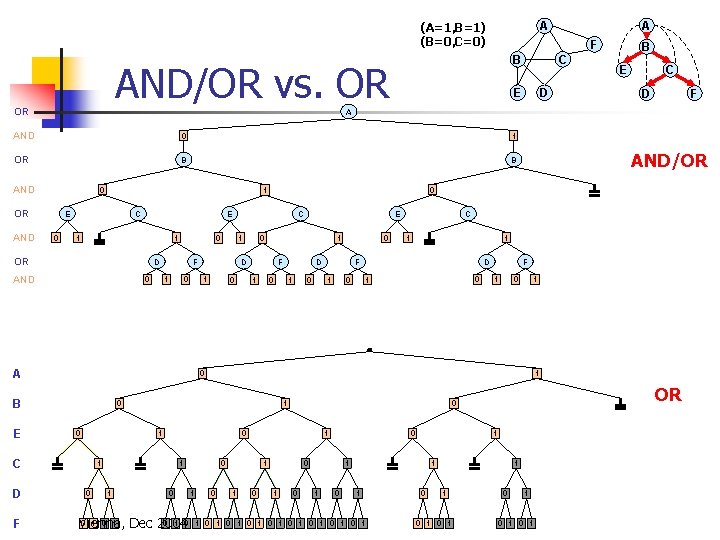
A A F B OR vs AND/OR OR E 0 1 OR B B AND 0 OR C D D F 0 C 1 OR 1 D AND 0 E 0 F 1 0 0 D 1 0 F 1 0 1 A 0 0 F 1 0 D 1 0 C 0 1 D 1 E C 1 AND/OR 0 1 E AND 1 1 0 0 1 D F 0 1 E F 1 0 0 D 1 0 1 0 C 1 0 0 1 1 0 1 0 1 D 1 F 0 1 0 D 1 0 F 1 0 1 1 0 1 0 1 1 0 0 0 1 OR 1 0 0 1 0 1 0 1 0 1 Vienna, Dec 2004 1 0 0 1 0 E C 1 F 0 B F E A AND D B C 0 1 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 1

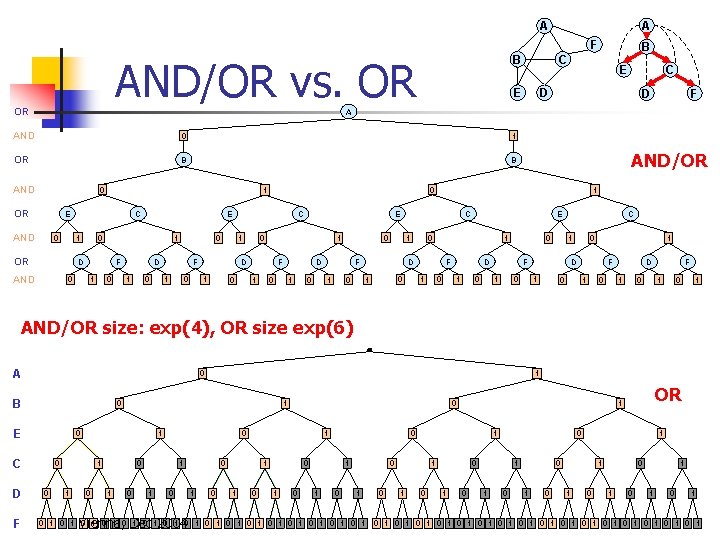
A A F AND/OR vs. OR OR B B C E E C D D F A AND 0 1 OR B B AND 0 OR AND 0 C 1 OR 0 E 0 1 D AND F 1 0 1 E 0 0 D 1 0 F 1 0 0 1 0 F 1 0 D 1 0 C 0 1 D 1 E C 1 AND/OR 1 1 0 0 1 D F 0 1 E F 1 0 0 D 1 0 1 F 1 0 C 0 1 D 1 F 0 1 0 D 1 0 F 1 0 1 AND/OR size: exp(4), OR size exp(6) A 0 B 0 E F 1 0 C D 1 1 0 0 0 1 1 0 0 Vienna, Dec 2004 1 0 1 1 0 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 0 0 0 1 OR 1 0 1 0 1 0 1 0 1 0 1 0 1

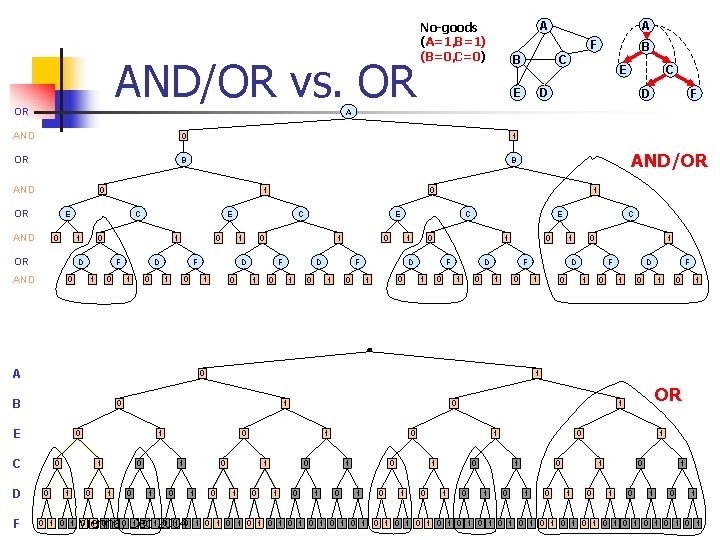
AND/OR vs. OR OR F B E C D D F A 0 1 OR B B AND 0 OR 0 C 1 OR 1 D AND 0 E 0 F 1 0 0 D 1 0 F 1 0 1 A 0 0 F 1 0 D 1 0 C 0 1 D 1 E C 1 AND/OR 0 1 E AND 1 1 0 0 1 D F 0 1 E F 1 0 0 D 1 0 1 0 C 1 0 0 1 1 0 Vienna, Dec 2004 1 0 1 1 D 1 F 0 1 0 D 1 0 0 0 F 1 0 1 1 0 E C 1 F 0 B F B C E AND D A A No-goods (A=1, B=1) (B=0, C=0) 0 1 1 0 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 0 0 0 1 OR 1 0 1 0 1 0 1 0 1 0 1 0 1

F B AND/OR vs. OR OR 1 OR B B AND 0 OR E 0 C E 1 1 0 D AND 0 1 0 0 0 F 1 0 1 D 1 E C 1 F A C D F AND/OR 0 D 1 0 C 1 1 D F 1 0 0 1 F 1 0 B 1 0 0 1 1 C F E 0 1 OR D D B A 0 E C E AND A A (A=1, B=1) (B=0, C=0) 0 1 1 0 0 1 0 1 0 Vienna, Dec 2004 1 0 1 1 0 0 0 1 OR 0 0 1 1 1 0 1 0 1 0 1 0 1 0 1

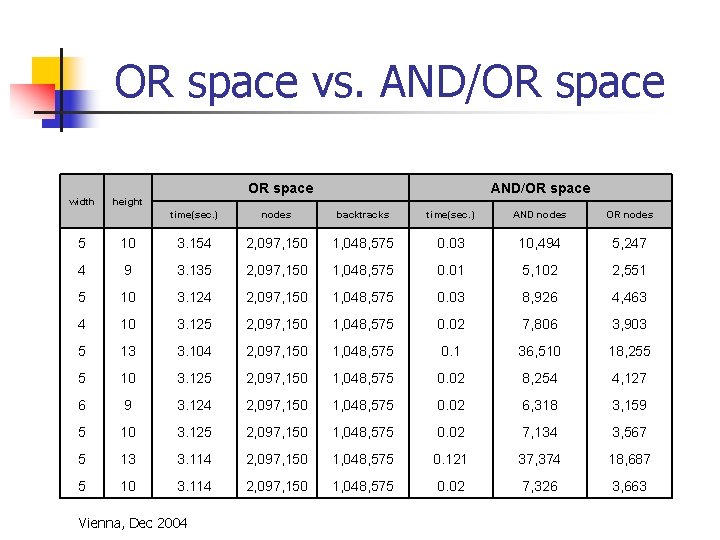
OR space vs. AND/OR space width AND/OR space height time(sec. ) nodes backtracks time(sec. ) AND nodes OR nodes 5 10 3. 154 2, 097, 150 1, 048, 575 0. 03 10, 494 5, 247 4 9 3. 135 2, 097, 150 1, 048, 575 0. 01 5, 102 2, 551 5 10 3. 124 2, 097, 150 1, 048, 575 0. 03 8, 926 4, 463 4 10 3. 125 2, 097, 150 1, 048, 575 0. 02 7, 806 3, 903 5 13 3. 104 2, 097, 150 1, 048, 575 0. 1 36, 510 18, 255 5 10 3. 125 2, 097, 150 1, 048, 575 0. 02 8, 254 4, 127 6 9 3. 124 2, 097, 150 1, 048, 575 0. 02 6, 318 3, 159 5 10 3. 125 2, 097, 150 1, 048, 575 0. 02 7, 134 3, 567 5 13 3. 114 2, 097, 150 1, 048, 575 0. 121 37, 374 18, 687 5 10 3. 114 2, 097, 150 1, 048, 575 0. 02 7, 326 3, 663 Vienna, Dec 2004

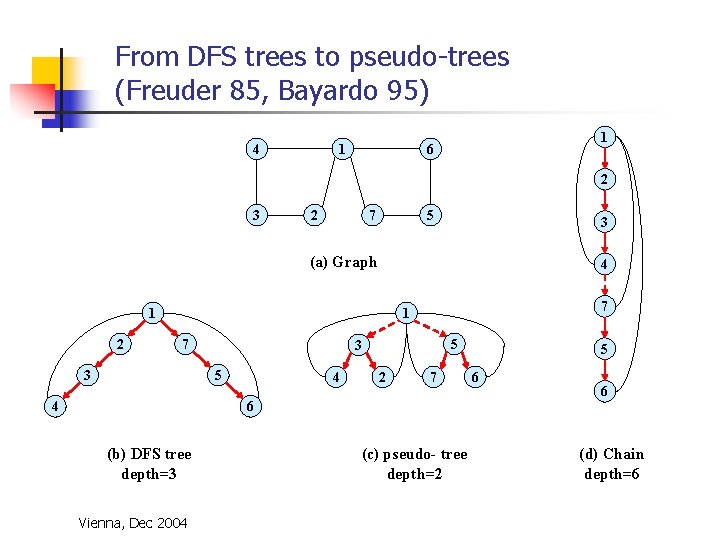
From DFS trees to pseudo-trees (Freuder 85, Bayardo 95) 4 1 1 6 2 3 2 7 5 3 (a) Graph 4 1 2 7 1 7 3 5 4 5 3 4 2 7 6 (b) DFS tree depth=3 Vienna, Dec 2004 (c) pseudo- tree depth=2 5 6 6 (d) Chain depth=6

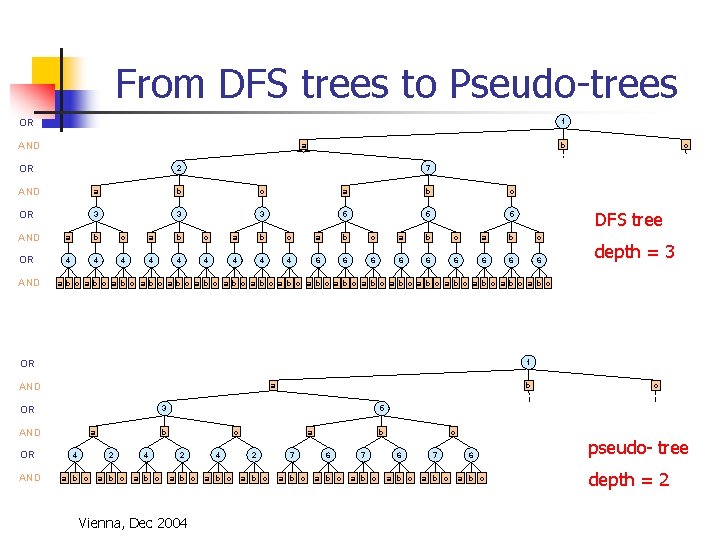
From DFS trees to Pseudo-trees OR 1 AND a OR b 2 7 AND a b c OR 3 3 3 5 5 5 DFS tree AND a b c a b c OR 4 4 4 4 4 6 6 6 6 6 AND 1 AND a OR b 3 AND depth = 3 a b c a b c a b c a b c a b c OR OR c a c 5 b c a b c 4 2 4 2 7 6 7 6 a b c a b c a b c Vienna, Dec 2004 pseudo- tree depth = 2

Finding min-depth backbone trees n n Finding min depth DFS, or pseudo tree is NPcomplete, but: Given a tree-decomposition whose tree-width is w*, there exists a pseudo tree T of G whose depth, satisfies (Bayardo and Mirankar, 1996, bodlaender and Gilbert, 91): m <= w* log n, Vienna, Dec 2004

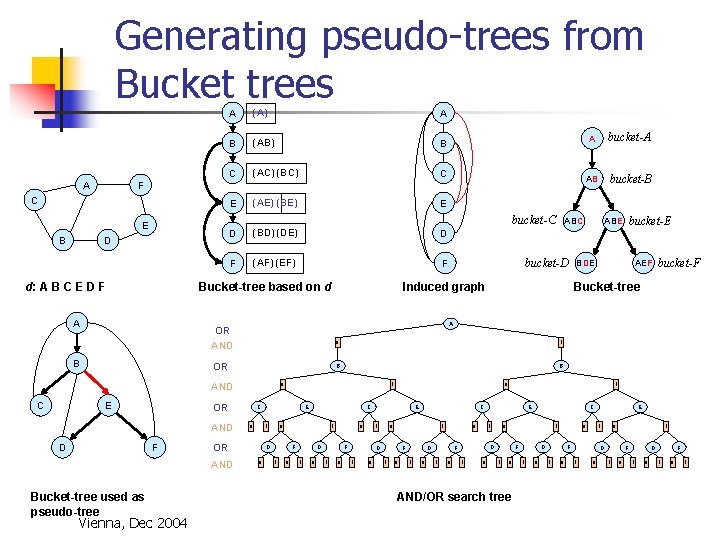
Generating pseudo-trees from Bucket trees A (A) A B (AB) B C (AC) (BC) C E (AE) (BE) E F C bucket-C E B A D d: A B C E D F D (BD) (DE) D F (AF) (EF) F Bucket-tree based on d A OR AND E D F Bucket-tree used as pseudo-tree Vienna, Dec 2004 bucket-B ABE bucket-E BDE AEF bucket-F Bucket-tree 1 B B 0 E 1 C 0 1 D 0 F 1 0 1 C OR AND bucket-D 0 0 OR AND AB A AND C bucket-A ABC Induced graph OR B A 0 0 D 1 0 F 1 0 0 0 F 1 0 1 D 1 C E 1 0 D 1 1 0 1 0 C 0 1 D F 1 E F 1 0 AND/OR search tree 0 D 1 0 1 F 1 0 E 0 1 D 1 0 F 1 0 1

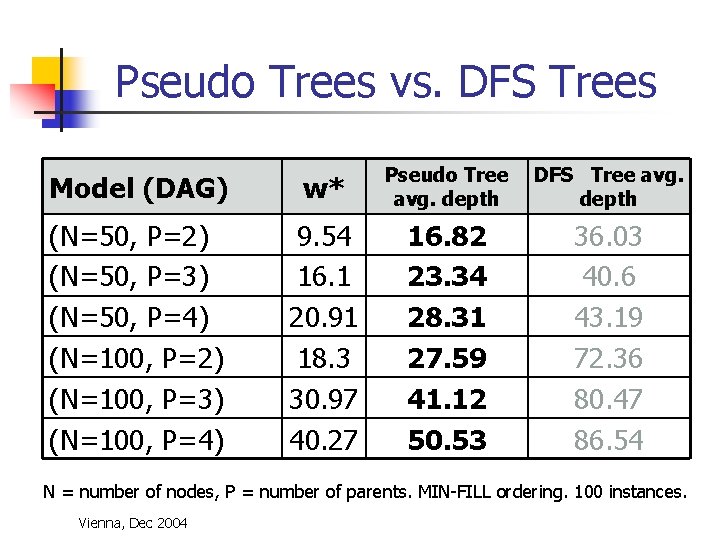
Pseudo Trees vs. DFS Trees Model (DAG) w* Pseudo Tree avg. depth (N=50, P=2) (N=50, P=3) (N=50, P=4) (N=100, P=2) (N=100, P=3) (N=100, P=4) 9. 54 16. 1 20. 91 18. 3 30. 97 40. 27 16. 82 23. 34 28. 31 27. 59 41. 12 50. 53 DFS Tree avg. depth 36. 03 40. 6 43. 19 72. 36 80. 47 86. 54 N = number of nodes, P = number of parents. MIN-FILL ordering. 100 instances. Vienna, Dec 2004

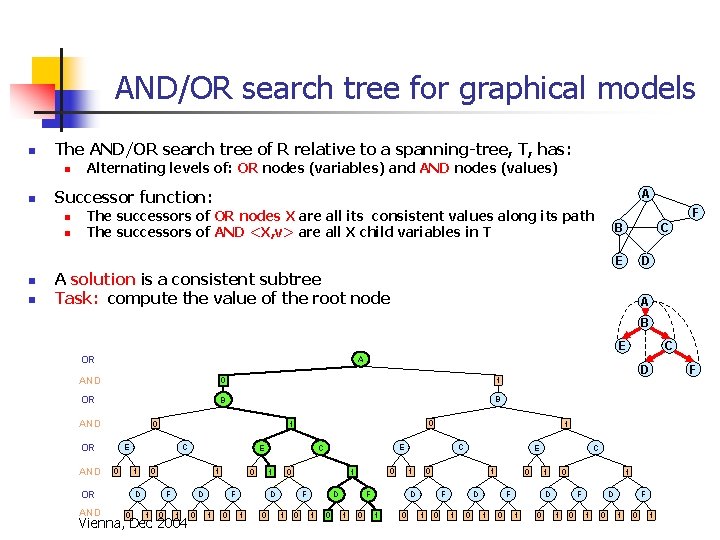
AND/OR search tree for graphical models n The AND/OR search tree of R relative to a spanning-tree, T, has: n n Alternating levels of: OR nodes (variables) and AND nodes (values) A Successor function: n n F The successors of OR nodes X are all its consistent values along its path The successors of AND <X, v> are all X child variables in T B C E n n D A solution is a consistent subtree Task: compute the value of the root node A B E OR AND 0 1 OR B B AND 0 OR AND 0 C 1 1 D 0 E 0 F 1 0 0 D 1 Vienna, Dec 2004 0 F 1 0 0 1 0 F 1 0 1 D 0 D 1 1 E C 1 D 0 1 E OR AND C A 0 1 0 E 0 1 D F 1 C F 1 0 0 D 1 0 1 F 1 0 C 0 1 D 1 0 F 1 0 1 F

AND/OR Search-tree properties (k = domain size, m = pseudo-tree depth. n = number of variables) n n Theorem: Any AND/OR search tree based on a pseudotree is sound and complete (expresses all and only solutions) Theorem: Size of AND/OR search tree is O(n km) Size of OR search tree is O(kn) n Theorem: Size of AND/OR search tree can be bounded by O(exp(w* log n)) n Related to: n When the pseudo-tree is a chain we get an OR space (Freuder 85; Dechter 90, Bayardo et. al. 96, Darwiche 1999, Bacchus 2003) Vienna, Dec 2004

Tasks and value of nodes n V( n) is the value of the tree T(n) for the task: n n n Consistency: v(n) is 0 if T(n) inconsistent, 1 othewise. Counting: v(n) is number of solutions in T(n) Optimization: v(n) is the optimal solution in T(n) Belief updating: v(n), probability of evidence in T(n). Partition function: v(n) is the total probability in T(n). n Goal: compute the value of the root node recursively using n Theorem: Complexity of AO dfs search is dfs search of the AND/OR tree. n n n Space: O(n) Time: O(n km) Time: O(exp(w* log n)) Vienna, Dec 2004

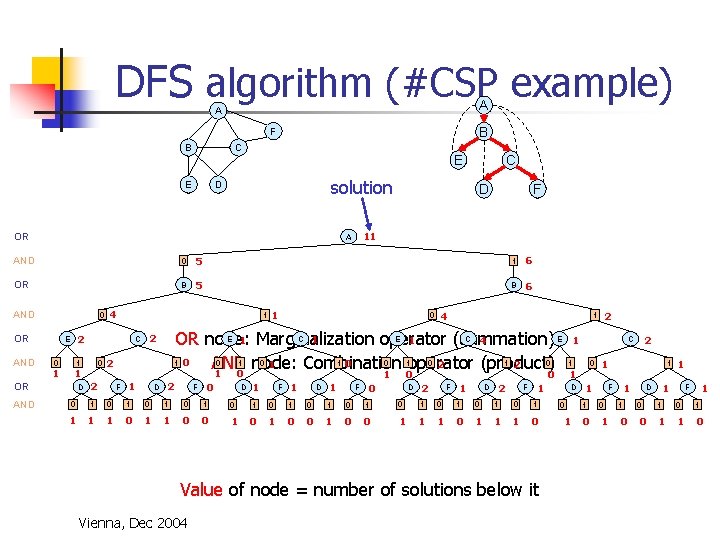
DFS algorithm (#CSP example) A A B F B C E E solution D OR C D F 11 A AND 0 5 1 6 OR B 5 B 6 AND 0 OR AND 0 1 0 D 2 2 F 1 D 1 0 4 1 2 F 0 D 1 F 1 D 1 F 0 0 0 1 0 1 1 1 1 0 0 1 0 0 D 0 1 F 1 D 2 F 1 0 1 0 1 1 1 0 0 1 D 0 1 2 C 1 1 Value of node = number of solutions below it Vienna, Dec 2004 1 0 2 2 1 E 1 C 4 E 1 Marginalization C 1 E OR node: operator (summation) 1 0 0 1 operator 0 2 1 2 0 1 node: 0 1 1 0 0 AND Combination (product) 1 0 2 C 1 OR AND 1 2 E 1 4 1 1 1 0 1 1 F 0 1 1 0 1 D 0 0 1 1 F 1 0 1 1 1 0

From Search Trees to Search Graphs n Any two nodes that root identical subtrees/subgraphs can be merged n Minimal AND/OR search graph: closure under merge of the AND/OR search tree n n Inconsistent subtrees can be pruned too. Some portions can be collapsed or reduced. Vienna, Dec 2004

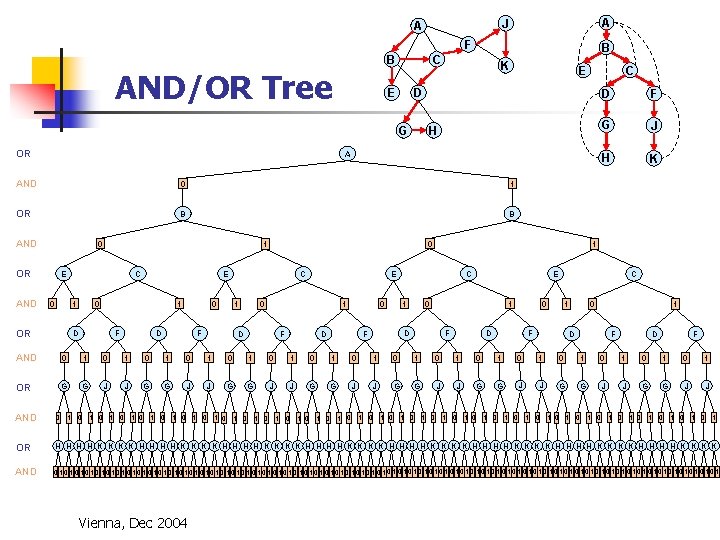
A J A F B AND/OR Tree E K C H A AND 0 1 OR B B AND 0 OR AND E D G OR B C E 0 C 1 OR 0 1 E 0 1 D F 0 D 1 F 0 0 1 D F D C 1 G J H K E 0 1 D F F 1 E C D F C 0 D 1 F 0 1 D F AND 0 1 0 1 0 1 0 1 OR G G J J G G J J AND 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 OR H H H H K K K K H H H H K K K K AND 0101010101010101010101010101010101010101010101010101010101010101 Vienna, Dec 2004

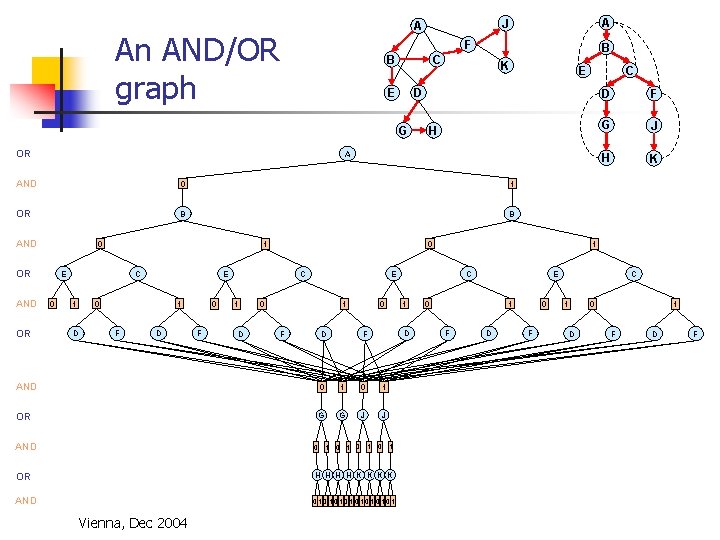
An AND/OR graph A J A F B E K A 0 1 OR B B AND 0 OR OR C H AND E D G OR B C E 0 C 1 D 0 1 E 0 1 F D 0 F 1 D 0 0 1 F D D F AND 0 1 OR G G J J AND 0 1 0 1 OR H H K K AND 01010101 Vienna, Dec 2004 C 1 F G J H K 1 E C D E 0 1 F D 0 F C 1 0 D 1 F D F

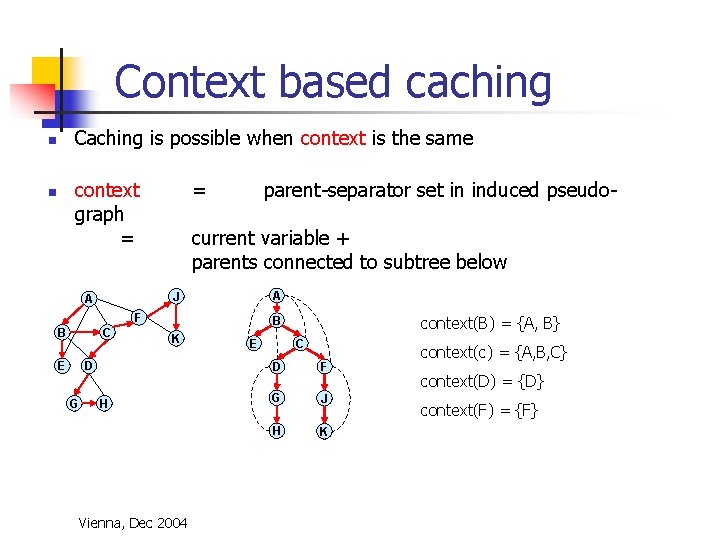
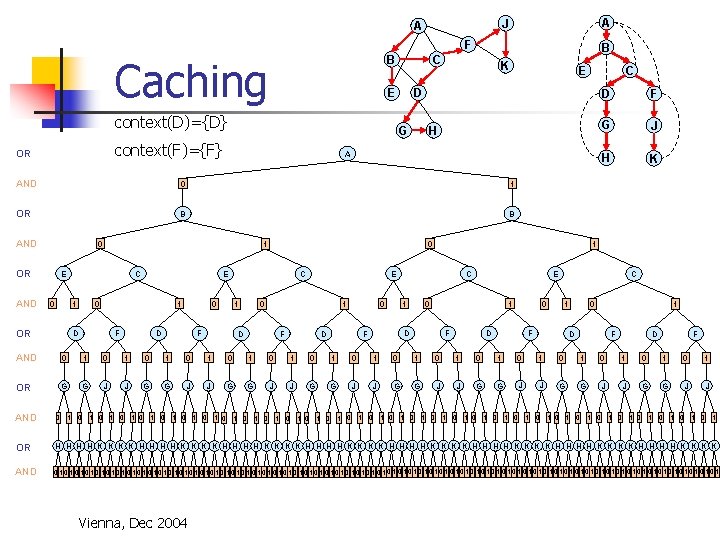
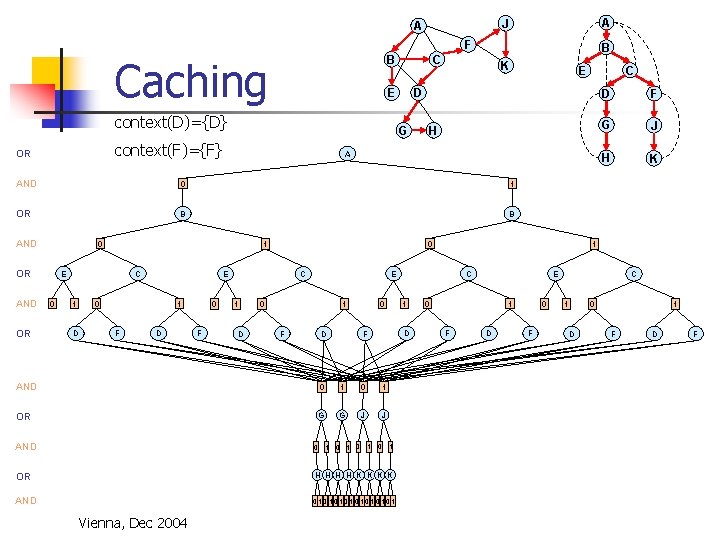
Context based caching Caching is possible when context is the same n context graph = n = parent-separator set in induced pseudo- current variable + parents connected to subtree below A J A F B C E K D G context(B) = {A, B} B H Vienna, Dec 2004 E C D F G J H K context(c) = {A, B, C} context(D) = {D} context(F) = {F}

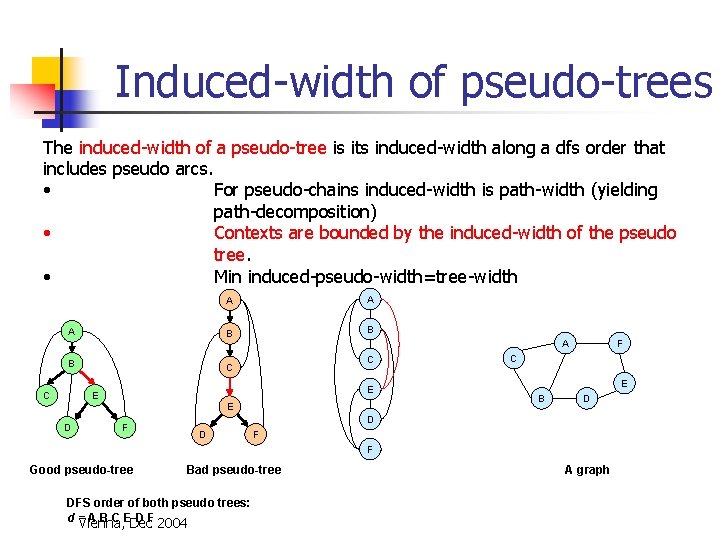
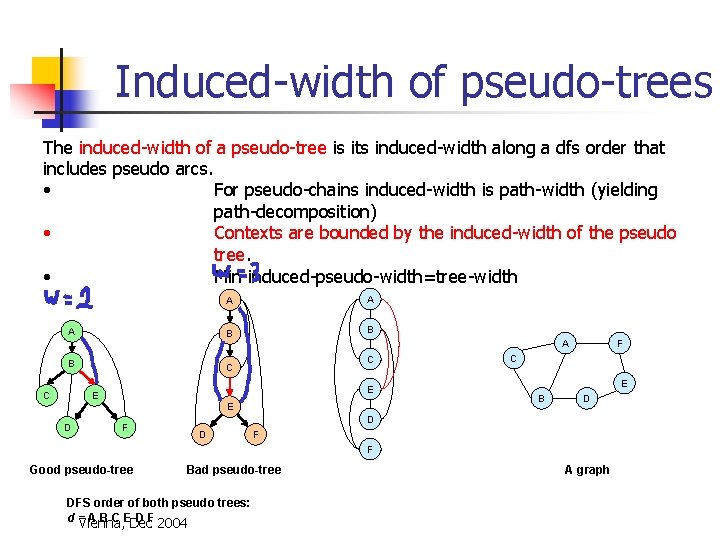
Induced-width of pseudo-trees The induced-width of a pseudo-tree is its induced-width along a dfs order that includes pseudo arcs. • For pseudo-chains induced-width is path-width (yielding path-decomposition) • Contexts are bounded by the induced-width of the pseudo tree. • Min induced-pseudo-width=tree-width A B C A A B B A C C E E E D F F C E B D D D F F Good pseudo-tree Bad pseudo-tree DFS order of both pseudo trees: d =Vienna, A B C EDec D F 2004 A graph

Induced-width of pseudo-trees The induced-width of a pseudo-tree is its induced-width along a dfs order that includes pseudo arcs. • For pseudo-chains induced-width is path-width (yielding path-decomposition) • Contexts are bounded by the induced-width of the pseudo tree. • Min induced-pseudo-width=tree-width A B C A A B B A C C E E E D F F C E B D D D F F Good pseudo-tree Bad pseudo-tree DFS order of both pseudo trees: d =Vienna, A B C EDec D F 2004 A graph

A J A F Caching B E context(D)={D} K A 0 1 OR B B 0 OR AND 0 C 1 OR 0 1 E E 0 1 D F 0 D C H AND E D G context(F)={F} OR B C 1 F 0 0 1 D F D C 1 G J H K E 0 1 D F F 1 E C D F C 0 D 1 F 0 1 D F AND 0 1 0 1 0 1 0 1 OR G G J J G G J J AND 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 OR H H H H K K K K H H H H K K K K AND 0101010101010101010101010101010101010101010101010101010101010101 Vienna, Dec 2004

A J A F Caching B E context(D)={D} K A 0 1 OR B B 0 OR AND OR 0 C 1 D 0 1 E E 0 1 F D 0 F 1 D 0 0 1 F D C 1 D F 0 1 OR G G J J AND 0 1 0 1 OR H H K K AND 01010101 D F G J H K 1 E C AND Vienna, Dec 2004 C H AND E D G context(F)={F} OR B C E 0 1 F D 0 F C 1 0 D 1 F D F

Size of minimal AND/OR context graphs Theorem: n n Minimal AND/OR context graph is bounded exponentially by its pseudo-tree induced-width. The tree-width of a pseudo-chain is path-width (pw) n Minimal OR search graph is O(exp(pw*)). Minimal AND/OR graph is O(exp(w*)) n Always, w* ≤ pw*, but pw*<= w* log n n Vienna, Dec 2004

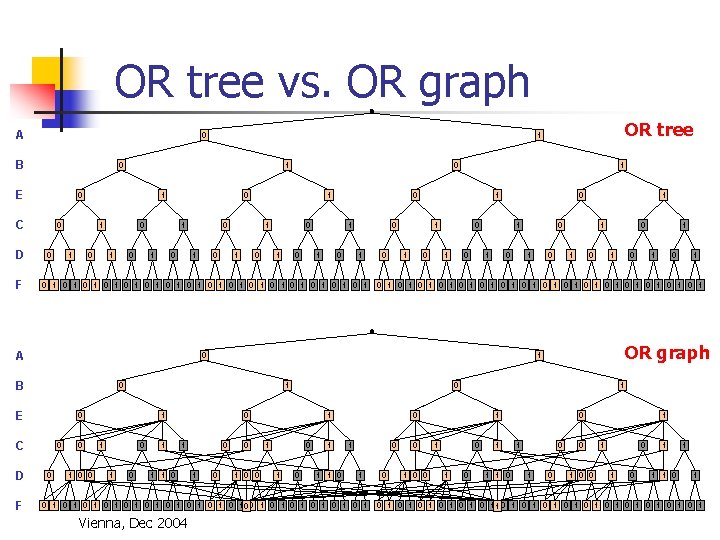
OR tree vs. OR graph A 0 B 0 E C D 1 0 0 1 1 0 0 1 0 1 OR tree 1 0 1 1 0 0 0 1 1 1 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 1 F 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 A 0 1 B 0 E 0 C D F 1 0 0 0 1 1 0 1 0 0 0 1 1 1 0 0 1 1 0 1 0 1 0 1 0 100 1 0 1 0 1 Vienna, Dec 2004 OR graph 0 0 1 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1

AND/OR tree vs. AND/OR graph OR A AND 0 1 OR B B AND 0 OR AND 0 C 1 OR 0 E 0 1 D AND F 1 0 1 E 0 0 D 1 0 F 1 0 0 1 0 F 1 0 1 D 0 D 1 1 E C 1 0 1 E 0 1 D F OR F 1 0 0 D 1 0 1 1 OR OR B B 1 D 1 0 F 1 0 1 A AND 0 0 OR AND 0 A 0 0 OR OR AND C 1 F OR AND AND AND/OR tree 0 0 C 1 1 0 D D E 0 0 1 1 E 1 1 0 F F 1 0 D D 1 Vienna, Dec 2004 0 0 F F 1 0 D D 0 0 0 1 1 0 F F 1 1 E C 1 AND/OR graph 0 D D 1 0 F F 1 C 0 0 1 0 D D E 1 1 1 0 F F 1 0 D D 0 1 0 0 F F 1 1 C 1 0 D D 0 0 1 1 1 0 F F 1 0 D D 1 0 F F 1

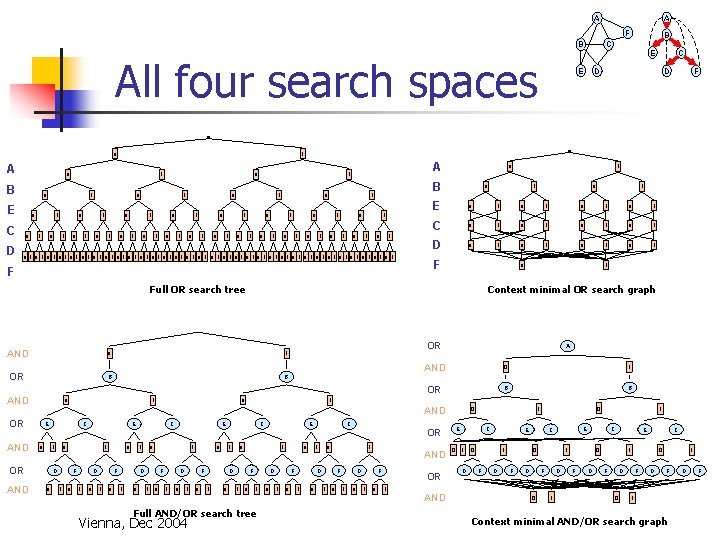
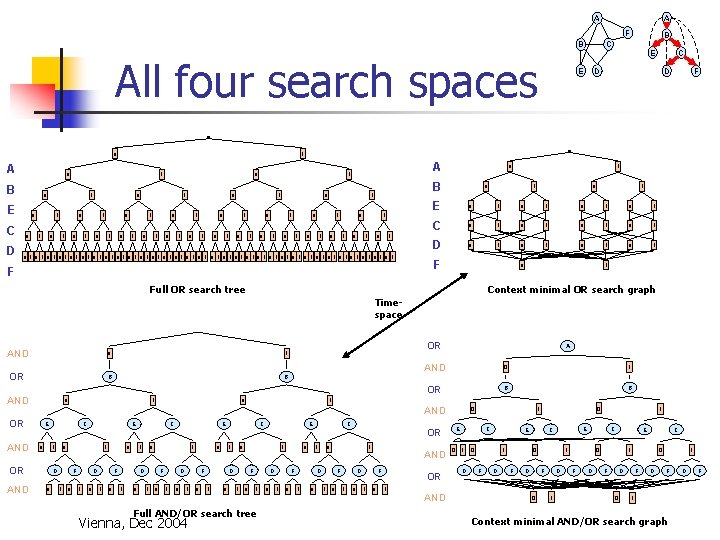
A A F B All four search spaces 0 A E 1 0 C D 1 0 0 1 1 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 0 1 A 1 0 1 0 0 1 1 0 1 F 0 1 OR B B AND 0 1 OR AND C 0 1 D 0 E F 1 0 0 D 1 0 1 F 1 0 0 D 1 0 F 1 0 D 1 0 0 1 F 1 0 0 D 1 Full AND/OR search tree Vienna, Dec 2004 E 0 D F 1 C 1 1 0 1 0 1 C 0 1 0 1 D 0 1 0 1 F 0 1 A AND 0 1 OR B B 1 E C 0 OR 0 1 1 E 0 AND 0 F Context minimal OR search graph AND E D 1 0 Full OR search tree OR C D 0 B 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 AND E E 1 0 B B C 0 1 F 1 0 C 0 1 D 1 0 F 1 0 AND D 1 E OR 0 F 1 0 OR 1 AND 0 C 1 D 0 1 E 0 1 F D E C 0 F D 0 C D 1 E 0 1 F D C 1 F D 0 0 F D 1 F 1 Context minimal AND/OR search graph D F

A A F B All four search spaces 0 A E 1 0 C D 1 0 0 1 1 0 0 1 0 1 E E C D D F 1 0 B B C 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 0 1 A 1 0 1 1 0 B 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 1 0 1 E 0 1 0 1 C 0 1 0 1 D 0 1 0 1 F 0 Full OR search tree 1 Context minimal OR search graph Timespace AND 0 1 OR B B AND 0 E 0 C 1 OR AND 0 1 A AND 0 1 OR B B 1 0 AND OR 0 1 D 0 E F 1 0 0 D 1 0 1 F 1 0 0 0 F 1 0 1 D 1 E C 0 D 1 0 1 0 1 F 1 0 0 D 1 Full AND/OR search tree Vienna, Dec 2004 E 0 D F 1 C 0 1 F 1 0 C 0 1 D 1 0 F 1 0 AND D 1 E OR 0 F 1 0 OR 1 AND 0 C 1 D 0 1 E 0 1 F D E C 0 F D 0 C D 1 E 0 1 F D C 1 F D 0 0 F D 1 F 1 Context minimal AND/OR search graph D F

AND/OR vs OR Graphs w*<=pw*<=m*<=w*log n (Bodlaendar et. Al, 1991) n Theorem: for balanced w-trees 1) and-or. Tree-size = or. Graph-size 2) Vienna, Dec 2004

Uniqueness of minimal AND/OR graph n Theorem: Given a pseudo-tree, the minimal n Related to compilation schemes: AND/OR search graph is unique for all graph-models that are consistent with that pseudo tree. n n n Minimal OR – related to OBDDs (Mc. Millan) Minimal AND/OR – related to tree-OBDDs (Mc. Millan 94), AND/OR graphs related to d-DNNF (Darwiche et. Al. 2002) Vienna, Dec 2004

Searching AND/OR Graphs n AO(i): searches depth-first, cache i-context n i = the max size of a cache table (i. e. number of variables in a context) i=0 i=w* Space: O(n) Space: O(exp w*) Time: O(exp(w* log n)) AO(i) time complexity? Vienna, Dec 2004 O(exp w*)

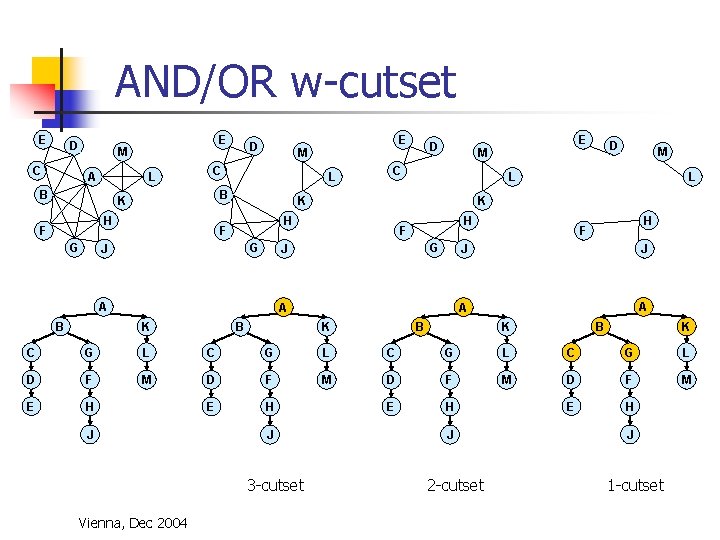
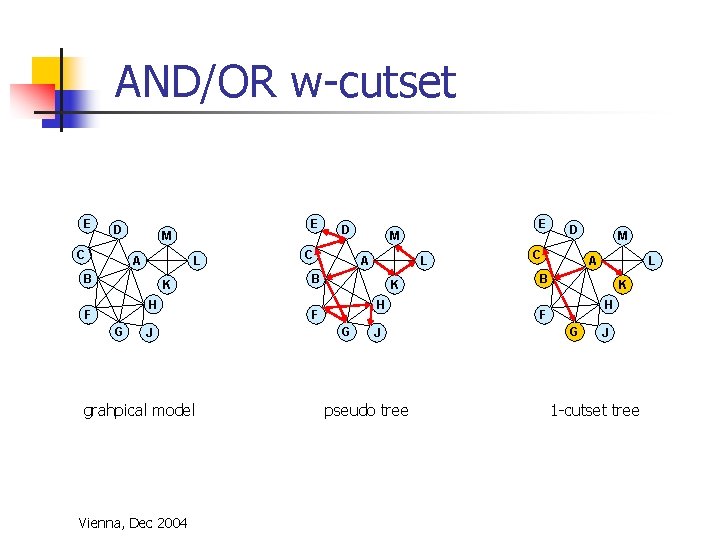
AND/OR w-cutset E D E M C A L B G L B H D C G B L H F G A K M L J A D K H F E M K J B E M C K F D K H F J J A A B B K K C G L D F M E H E H J J 3 -cutset Vienna, Dec 2004 J 2 -cutset J 1 -cutset

AND/OR w-cutset E D C E M A L B K H F G J grahpical model Vienna, Dec 2004 D C A L B K H F G E M J pseudo tree D C M A L B K H F G J 1 -cutset tree

Searching AND/OR Graphs n AO(i): searches depth-first, cache i-context n i = the max size of a cache table (i. e. number of variables in a context) i=0 i=w* i Space: O(n) Space: O(exp w*) Time: O(exp(w* log n)) Vienna, Dec 2004 Space: O(exp(i) ) Time: O(exp(m_i+i ) O(exp w*)

Overview n Introduction and background for graphical models: inference and search n Inference: n n n AND/OR search spaces for graphical models n n Exact: Tree-clustering, variable elimination, Approximate: mini-bucket, belief propagation mixed networks Empirical evaluation over mixed networks, counting Vienna, Dec 2004

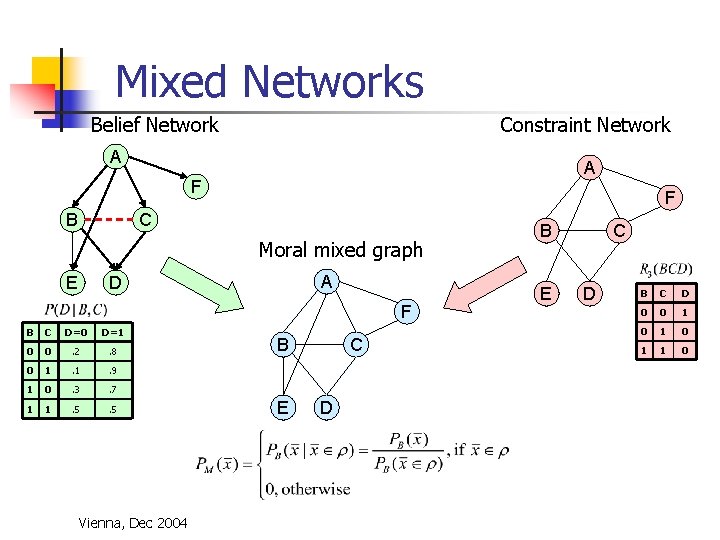
Mixed Networks Belief Network Constraint Network A A F B F C Moral mixed graph E A D F B C D=0 D=1 0 0 . 2 . 8 0 1 . 9 1 0 . 3 . 7 1 1 . 5 Vienna, Dec 2004 B E C D B C D 0 0 1 0 1 1 0

Using look-ahead – example (1) A B C C G H I K D E > G H All domains are {1, 2, 3, 4} Vienna, Dec 2004 I F > E > D > > > B > > A K

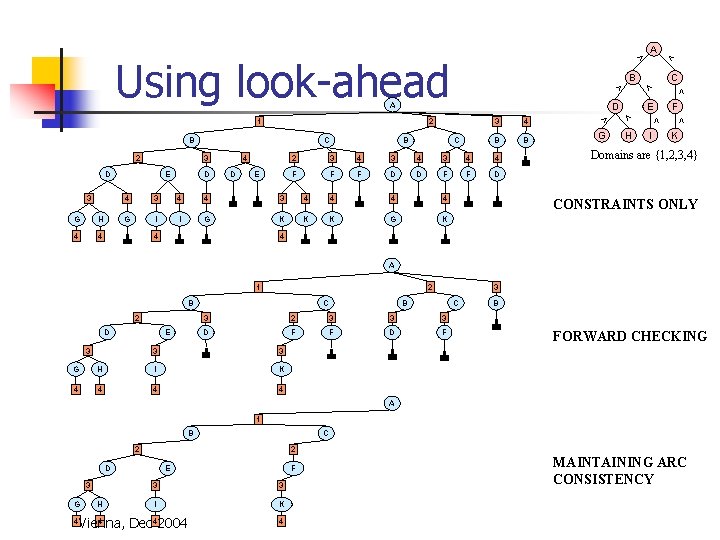
2 D 3 G H 4 4 E D 4 D E C B B 4 3 4 4 F F F D D F F D 4 4 3 4 4 G I I G K K K G K > G > H I > 4 3 3 4 3 2 4 F > B E > C 3 D 2 B C > A 1 > B A > Using look-ahead > K Domains are {1, 2, 3, 4} CONSTRAINTS ONLY 4 A 1 2 B 2 D E 3 C 3 B C 3 2 3 3 3 D F F D F 3 3 G H I K 4 4 B FORWARD CHECKING A 1 B C 2 2 D 3 G 4 H E F 3 3 I K 4 Vienna, Dec 42004 4 MAINTAINING ARC CONSISTENCY

Experiments – mixed networks n n Belief network - (N, K, R, P): n n n Parameters of the mixed networks: n N = number of variables n K = number of values per variable n R = number of root nodes P = number of parents n n Measures: n n n Constraint network - (N, K, C, S, t): n Time Number of nodes Number of dead-ends n C = number of constraints S = scope size of the constraints t = tightness (no. of disallowed tuples) Algorithms: n n n AO-C AO-FC AO-RFC constraint checking only forward checking relational forward checking OR vs. AND/OR Spaces Vienna, Dec 2004

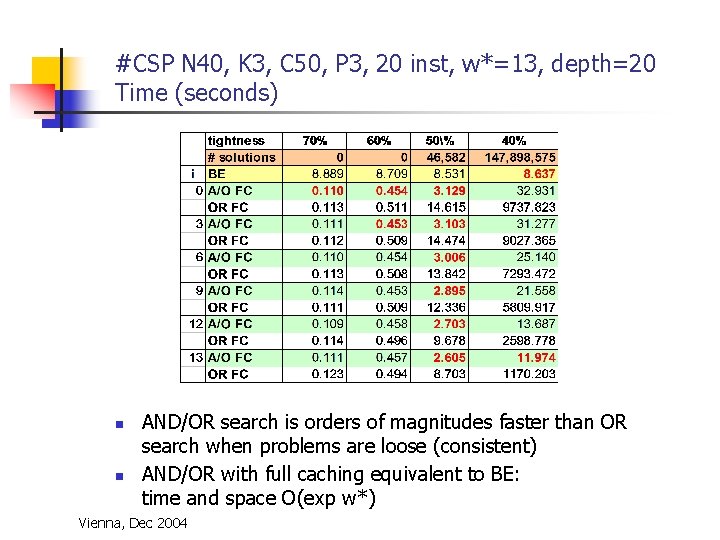
#CSP N 40, K 3, C 50, P 3, 20 inst, w*=13, depth=20 Time (seconds) n n AND/OR search is orders of magnitudes faster than OR search when problems are loose (consistent) AND/OR with full caching equivalent to BE: time and space O(exp w*) Vienna, Dec 2004

Mixed networks results (1) n n Caching helps more on loose problems Constraint propagation helps more on tight problems Vienna, Dec 2004

Conclusion n AND/OR search spaces are a unifying framework for search or compilation applicable to any graphical models. n With caching AND/OR is similar to inference (minimal graphs) n AND/OR time and space bounds are equal to state of the art algorithms n Empirical results n n AND/OR search spaces are always more effective than traditional OR spaces AND/OR allows a flexible tradeoff between space and time n Graphical models should always use AND/OR search with embeded inference. n Current work: Hybrid of inference and search: Heuristic generation and Branch and Bound Vienna, Dec 2004