Expected Shortfall e Misure Spettrali di Rischio Un

Expected Shortfall e Misure Spettrali di Rischio: Un’ indagine critica sul concetto di rischio finanziario PASSEPARTOUT – Milano Bicocca – 18 Giugno 2002

Schema della presentazione 1. Definire una Misura di Rischio: i. Value at Risk (Va. R) ii. Expected Shortfall (ES) iii. Misure Coerenti di Rischio iv. Definizione Coerente di ES: alcune sottigliezze matematiche 2. Misure Spettrali di Rischio i. “Subjective Risk Aversion” e Misure Coerenti. ii. La “Risk Aversion Function”

Argomento: solo finanza (e un po’ di statistica) Le domande del Risk Manager Finanziarie Che cosa misuro ? Statistiche Come stimo la misura ? La nostra indagine è dedicata solo a temi finanziari e statistici. Probabilistiche Computazionali I risultati saranno peraltro assolutamente Che ipotesi generali Che computer devo fare ? mi serve ?

Parte 1: Definire una Misura di Rischio

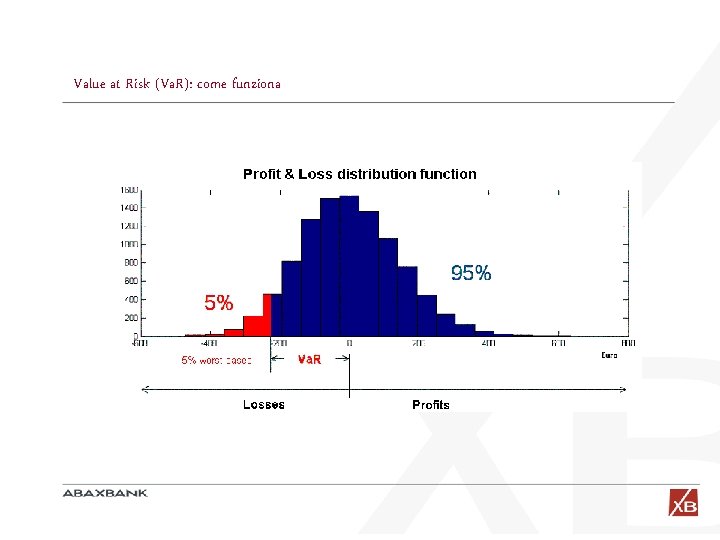
Value at Risk (Va. R): come funziona Per quanto sembri strana Per calcolare il Va. R di un portafoglio si deve fissare: questa è la più frequente domanda l Un orizzonte temporale: ad esempio un giorno. Rappresenta il periodo futuro di osservazione. l Un livello di confidenza: ad esempio una probabilità del 5%. Rappresenta la frazione scelta di “casi nella gestione del rischio finanziario peggiori” per il portafoglio. Il Va. R è definito da “Il Va. R di un portafoglio è la perdita minima che esso può subire in un giorno nel 5% di casi peggiori” O analogamente, “Il Va. R di un portafoglio è la perdita massima che esso può subire in un giorno nel 95% di casi migliori”

Value at Risk (Va. R): come funziona

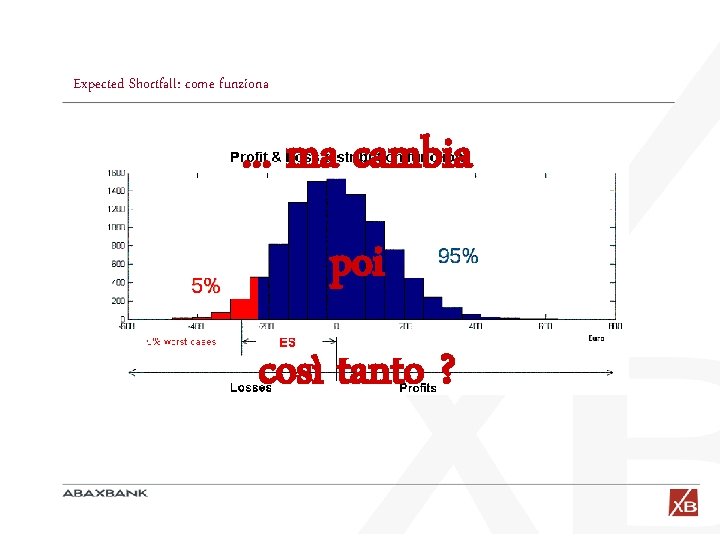
L’Expected Shortfall come evoluzione del Va. R Definizione di Expected Shortfall: “L’ ES di un portafoglio è la perdita media che esso può subire in un giorno nel 5% di casi peggiori” Mentre “Il Va. R di un portafoglio è la perdita minima che esso può subire in un giorno nel 5% di casi peggiori” ES = la media dei casi peggiori Va. R = il migliore dei casi peggiori

Expected Shortfall: come funziona . . . ma cambia poi così tanto ?

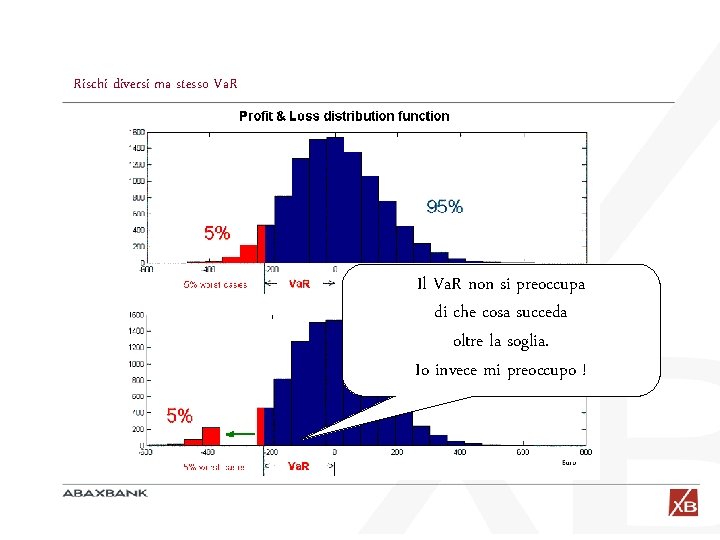
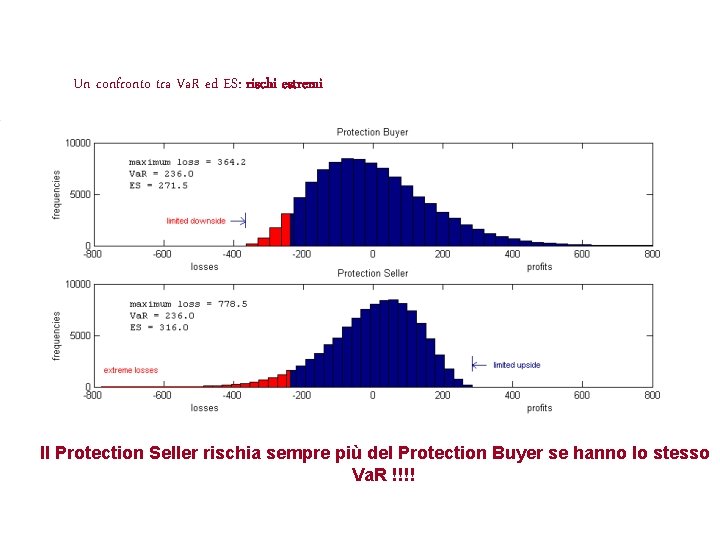
Rischi diversi ma stesso Va. R Il Va. R non si preoccupa di che cosa succeda oltre la soglia. Io invece mi preoccupo !

Protection Selling. . . Possiamo classificare gli strumenti o portafogli finanziari in due categorie: Ø Protection Seller Position: è una posizione finanziaria tipicamente soggetta a rischi molto elevati ma di probabilità molto bassa, con profitti relativamente modesti ma molto probabili. Øes: una compagnia di assicurazione che percepisce una polizza annua ma garantisce l’indennizzo dei danni derivanti da una catastrofe. Øes: un investitore che compra un bond soggetto a rischio di default, scommettendo in interessi vantaggiosi ma incorrendo nel rischio che l’emittente fallisca. Øes: una posizione “corta in opzioni” (Put o Call che siano). Øes: tutte le posizioni in derivati cosiddette “corte di volatilità”

. . . e Protection Buying Il viceversa è costituito da. . . Protection Buying Position: è una posizione finanziaria tipicamente soggetta a rischi limitati ma di probabilità relativamente alta, con profitti molto elevati o anche potenzialmente illimitati ma dall’eventualità remota. Øes: il sottoscrittore della polizza assicurativa a protezione di un rischio da catastrofe Øes: un giocatore di totocalcio che compri una schedina a due colonne. Øes: un investitore che compri un Warrant (Call o Put che sia. . . ) Øes: tutte le posizioni in derivati “lunghe di volatilità”

Un confronto tra Va. R ed ES: rischi estremi Il Protection Seller rischia sempre più del Protection Buyer se hanno lo stesso Va. R !!!!

1997: qualcuno comincia a sollevare pesanti critiche al Va. R “(…) The basic reasons to reject the value at risk measure of risks are the following: (a) value at risk does not behave nicely with respect to addition of risks (…) creating severe aggregation problems. (b) the use of value at risk does not encourage and, indeed, sometimes prohibits diversification, because value at risk does not take into account the economic consequences of the events the probabilities of which it controls” P. Artzner, F. Delbaen, et al, 1999, “Coherent Measures of Risk”, see http: //www. math. ethz. ch/~delbaen “Can Va. R be used to allocate capital? This question is much related to the nonsubadditivity of Va. R (…) Va. R is more than questionable” P. Embrechts, “Extreme Value Theory: potential and limitations as an integrated Risk Management Tool”, 1999, see http: //www. math. ethz. ch/~embrechts

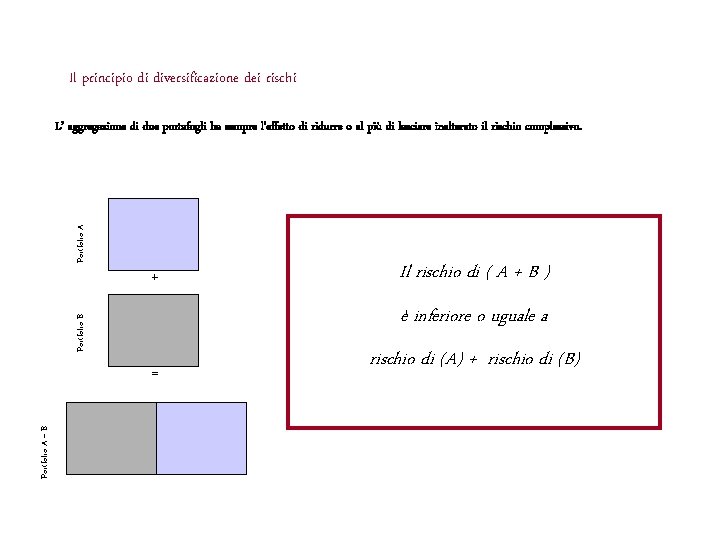
Il principio di diversificazione dei rischi Portfolio A L’ aggregazione di due portafogli ha sempre l’effetto di ridurre o al più di lasciare inalterato il rischio complessivo. + Portfolio B è inferiore o uguale a = Portfolio A + B Il rischio di ( A + B ) rischio di (A) + rischio di (B)

Il principio di diversificazione finisce qui Misure Coerenti di Rischio In un celebre articolo “Coherent measures of Risk” (Artzner, Delbaen, Eber, Heath Mathematical Finance, Luglio 1999) venne proposto un insieme di assiomi per definire i requisiti fondamentali di una “misura coerente di rischio”. (Monotonicità) se (Omogeneità Positiva) se allora (Invarianza Translazionale) (Subadditività) Il Va. R vìola questo assioma

Ma che cosa significa “misura coerente di rischio” ? Una misura è coerente se attribuisce sempre valori maggiori a rischi più elevati Una misura che non sia coerente può quindi aumentare al diminuire del rischio e viceversa. Quindi. . . . una misura non coerente non è una misura di rischio

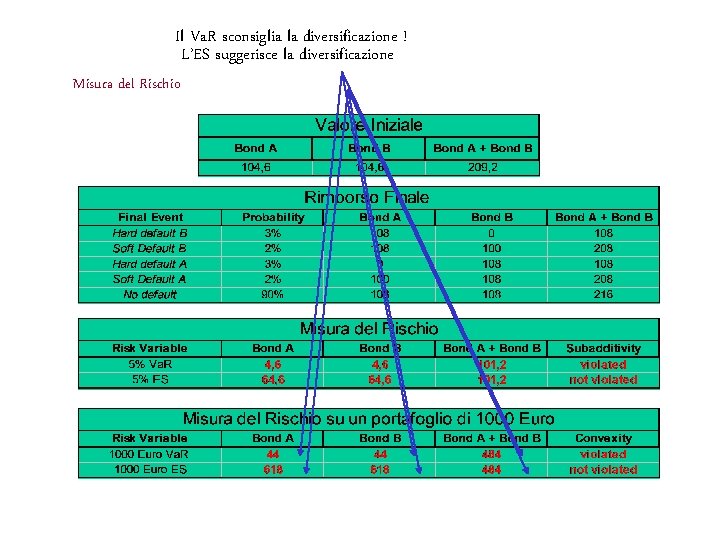
Una violazione di subadditività del Va. R Consideriamo un Bond A e supponiamo che, a maturità, ci siano tre possibilità: 1) No default: rimborsa il nominale (100 Euro) e la cedola (8 Euro) 2) Soft default: rimborsa solo il nominale (100 Euro) 3) Hard Default: non rimborsa nulla

Una violazione di subadditività del Va. R Consideriamo un altro Bond B identico ad A, ma di diverso emittente Supponiamo inoltre che i rischi di default dei due bond siano mutuamente esclusivi e cioè che i due emittenti A e B non facciano mai default assieme. Caso tipico: RISCHI ANTICORRELATI = RIDUZIONE DEL RISCHIO IN CASO DI DIVERSIFICAZIONE

Il Va. R sconsiglia la diversificazione ! L’ES suggerisce la diversificazione Misura del Rischio

Non-coerenza del Va. R L’esempio precedente mette in luce i tipici problemi del Va. R l Il Va. R può scoraggiare la diversificazione (non è subadditivo) l Il Va. R, fornisce un valore inferiore (44) per un portafoglio più rischioso (1000 Euro di bond A) e un valore maggiore (484) per un portafoglio meno rischioso (1000 Euro di A+B diversificati). Il Va. R non è coerente

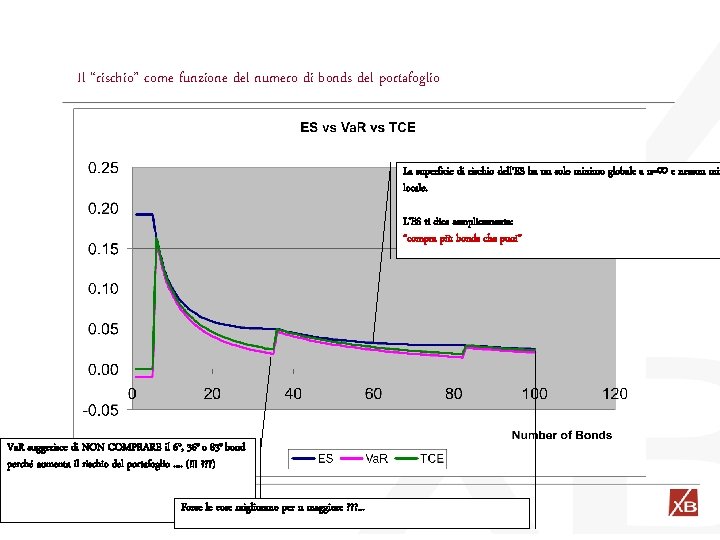
Un portafoglio prototipo Si consideri un portafoglio di n bonds rischiosi tutti con probabilità di default del 2% e si supponga per semplicità che tutte le probabilità di default siano tra loro indipendenti. Portfolio = { 100 Euro investiti in n Bonds indipendenti ugualmente rischiosi} Bond payoff = Nominale (o 0 con probabilità del 2%) Domanda: si scelga n in modo da minimizzare il rischio del portafoglio Proviamo a vedere come rispondono a questa domanda il Va. R, l’ES e TCE con livello di confidenza al 5% e orizzonte temporale uguale alla maturità del bond.

Il “rischio” come funzione del numero di bonds del portafoglio La superficie di rischio dell’ES ha un solo minimo globale a n= e nessun min locale. L’ES ti dice semplicemente: “compra più bonds che puoi” Va. R suggerisce di NON COMPRARE il 6 o, 36 o o 83 o bond perché aumenta il rischio del portafoglio. . (!!! ? ? ? ) Forse le cose migliorano per n maggiore ? ? ? . . .

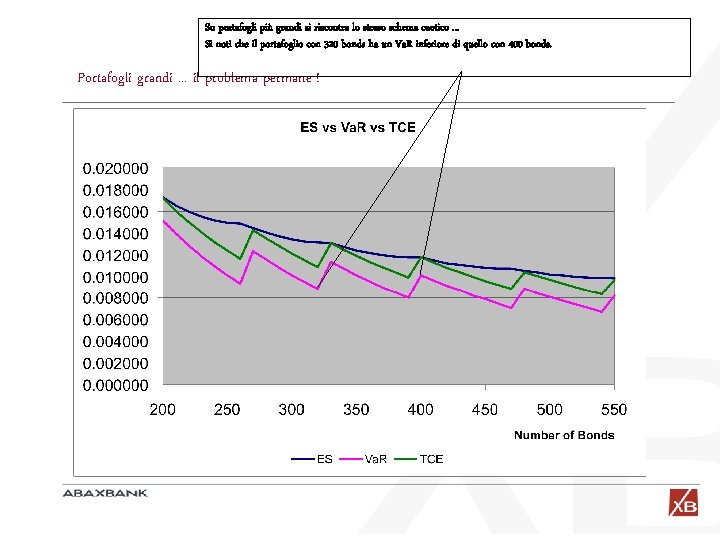
Su portafogli più grandi si riscontra lo stesso schema caotico. . . Si noti che il portafoglio con 320 bonds ha un Va. R inferiore di quello con 400 bonds. Portafogli grandi. . . il problema permane !

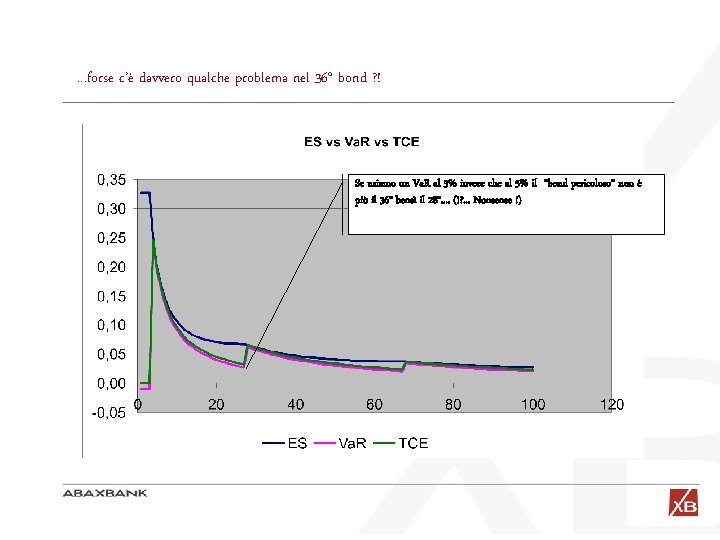
. . . forse c’è davvero qualche problema nel 36 o bond ? ! Se usiamo un Va. R al 3% invece che al 5% il “bond pericoloso” non è più il 36 o bensì il 28 o. . (!? . . . Nonsense !)

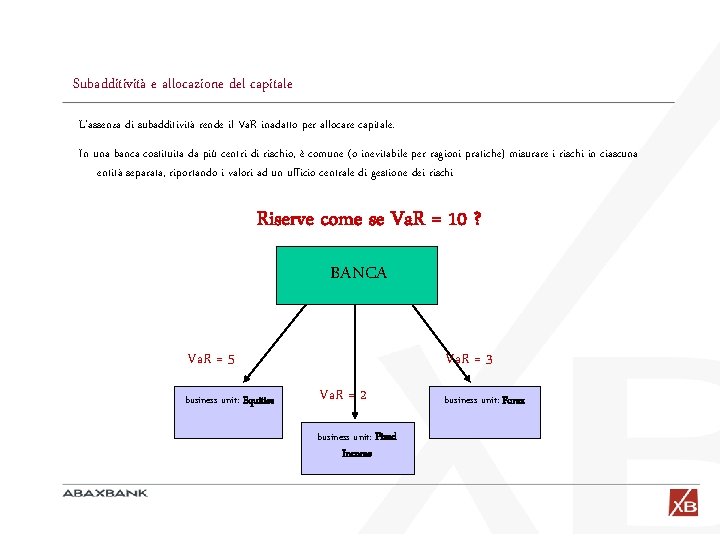
Subadditività e allocazione del capitale L’assenza di subadditività rende il Va. R inadatto per allocare capitale. In una banca costituita da più centri di rischio, è comune (o inevitabile per ragioni pratiche) misurare i rischi in ciascuna entità separata, riportando i valori ad un ufficio centrale di gestione dei rischi Riserve come se Va. R = 10 ? BANCA Va. R = 5 business unit: Equities Va. R = 3 Va. R = 2 business unit: Fixed Income business unit: Forex

Subadditività e vigilanza bancaria Disponendo dei singoli valori di Va. R per le diverse Business Units, è consuetudine provvedere ad accantonamenti ai fini della Vigilanza bancaria per ciascuno di questi Valori di Va. R. Ma questo equivale a credere che il Va. R sia SUBADDITIVO ! l Va. R Equity = 5 l Va. R Forex = 3 Riserve per un Va. R = 10 ? l Va. R Bonds = 2 . . . ma il Va. R della banca può essere anche molto superiore a 10

E l’Expected Shortfall è coerente ? La definizione originale di Expected Shortfall (anche nota come TCE, CVa. R o Expected Loss) è Anche questa misura NON è SUBADDITIVA in generale e quindi NON è COERENTE. Si può mostrare che è subadditiva se la distribuzione delle perdite è continua. Nel caso di distribuzioni generali tuttavia essa non gode di subadditività.

2001: una definizione coerente di Expected Shortfall Febbraio 2001: nuova definizione di Expected Shortfall Dimostrazione generale di coerenza: C. Acerbi, C. Nordio and C. Sirtori, “Expected Shortfall as a Tool of Financial Risk Management” http: //www. aifirm. com/archivio/Pubblicazioni/Expected%20 Shortfall%20 as. pdf Nel caso di distribuzioni continue essa coincide con La dimostrazione di coerenza vale senza alcuna ipotesi sulla distribuzione.

Stimare l’Expected Shortfall Si può dimostrare (Acerbi, Tasche 2001) che l’ES è effettivamente stimabile in modo consistente tramite il semplice stimatore “Media dei 100 % casi peggiori”. Ordered statistics (= dati ordinati dal peggiore al migliore)

Parte 2: Misure Spettrali di Rischio

Una domanda naturale L’ Expected Shortfall è un caso isolato o esiste una classe più ampia di misure coerenti di rischio ? E’ possibile costruire nuove misure coerenti a partire da misure coerenti note ? La risposta è semplice e consente di generare un’intera CLASSE di misure coerenti. Date n misure di rischio coerenti 1, 2, . . . n qualsiasi combinazione lineare convessa = 1 1 + 2 2 +. . . + n n ( con k k = 1 e k>0 ) è una MISURA COERENTE

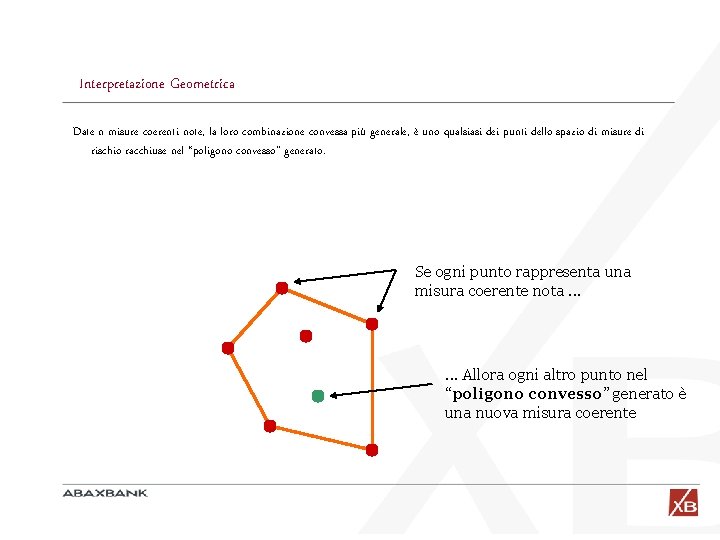
Interpretazione Geometrica Date n misure coerenti note, la loro combinazione convessa più generale, è uno qualsiasi dei punti dello spazio di misure di rischio racchiuse nel “poligono convesso” generato. Se ogni punto rappresenta una misura coerente nota. . . Allora ogni altro punto nel “poligono convesso” generato è una nuova misura coerente

La nostrategia. . Ma noi conosciamo già infinite misure coerenti di rischio, date da tutte le possibili -Expected Shortfalls per ogni valore di compreso tra 0 e 1 Perciò possiamo generare un nuovo spazio di misure coerenti. Questa classe verrà definita “Misure Spettrali di Rischio” Insieme di Expected Shortfalls con (0, 1] Poligono Convesso = Nuovo spazio di misure coerenti

Misure Spettrali: La classe di Misure Spettrali di Rischio può essere facilmente parametrizzata come imponendo opportune condizioni sullo Spettro di Rischio definito sull’intervallo [0, 1]. Si noti che questa parametrizzazione contiene sia il Va. R che l’ES: Va. R: Funzione a Gradino di Heaviside Delta di Dirac

Misure Spettrali di Rischio Teorema: (Acerbi 2001) la Misura Spettrale di Rischio è coerente se e solo se il suo Spettro di Rischio soddisfa 1. è positivo 1. è decrescente 1.

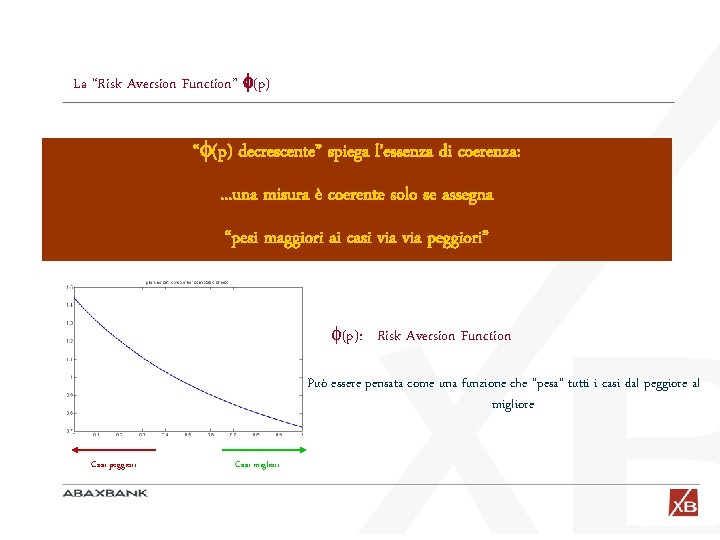
La “Risk Aversion Function” (p) Ogni ammissibile (p) rappresenta possibile legittimospiega atteggiamento razionalediverso il rischio “ (p) undecrescente” l’essenza coerenza: Un investitore razionale può esprimere la propria soggettiva avversione verso il rischio mediante la sua soggettiva (p). . . una misura è coerente solo se assegna ottenendo la sua misura coerente spettrale M “pesi maggiori ai casi via peggiori” (p): Risk Aversion Function Può essere pensata come una funzione che “pesa” tutti i casi dal peggiore al migliore Casi peggiori Casi migliori

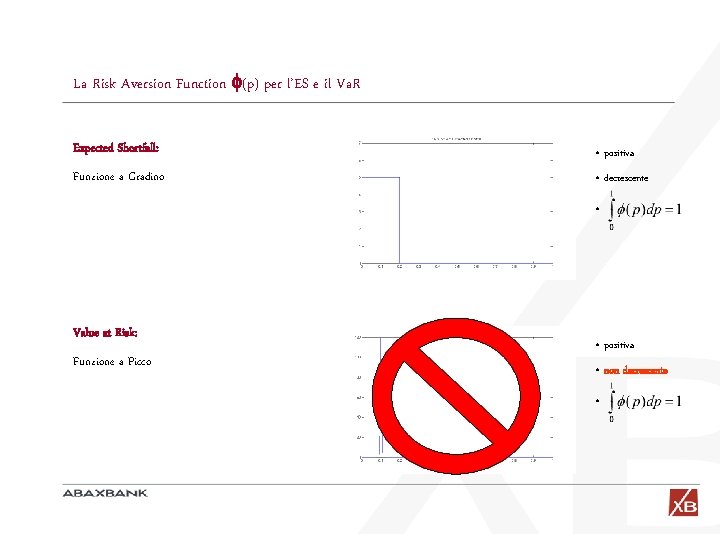
La Risk Aversion Function (p) per l’ES e il Va. R Expected Shortfall: • positiva Funzione a Gradino • decrescente • Value at Risk: Funzione a Picco • positiva • non decrescente •

Stimare le Misure Spettrali di Rischio Si può dimostrare (Acerbi 2001) che ogni misura spettrale ha il seguente stimatore consistente: Ordered statistics (= dati ordinati dal peggiore al migliore) Funzione discretizzata

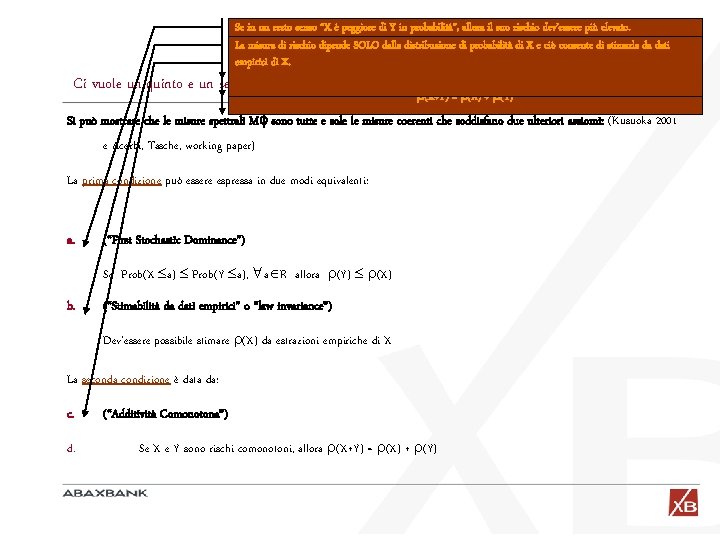
Ci vuole un quinto e un Se in un certo senso “X è peggiore di Y in probabilità”, allora il suo rischio dev’essere più elevato. La misura di rischio dipende SOLO dalla distribuzione di probabilità di X e ciò consente di stimarla da dati empirici X. “perfettamente correlati”, allora il rischio della somma X+Y dev’essere esattamente pari alla somma Se X e Ydisono dei rischi di X e? Y. sesto assioma (X+Y) = (X) + (Y) Si può mostrare che le misure spettrali M sono tutte e sole le misure coerenti che soddisfano due ulteriori assiomi: (Kusuoka 2001 e Acerbi, Tasche, working paper) La prima condizione può essere espressa in due modi equivalenti: a. (“First Stochastic Dominance”) Se Prob(X a) Prob(Y a), a R allora (Y) (X) b. (“Stimabilità da dati empirici” o “law invariance”) Dev’essere possibile stimare (X) da estrazioni empiriche di X La seconda condizione è data da: c. d. (“Additività Comonotona”) Se X e Y sono rischi comonotoni, allora (X+Y) = (X) + (Y)

Conclusioni l Lo spazio delle Misure Spettrali M fornisce la rappresentazione di tutte le misure coerenti di rischio che si prestano ad applicazioni concrete. l Ogni misura coerente di questo spazio è in corrispondenza biunivoca con ogni forma razionale di avversione al rischio di un investitore. l Per ogni misura spettrale M è disponibile uno stimatore empirico consistente. l L’applicazione concreta di qualsiasi misura spettrale è elementare. l L’ES non gioca alcun ruolo privilegiato all’interno delle Misure Spettrali. l Il Value at Risk da questo punto di vista risulta del tutto inadeguato per la descrizione e misurazione dei rischi di un portafoglio. E’ associabile ad un atteggiamento al rischio non razionale.

Riferimenti

Riferimenti