Estatstic a Prof Edson Nemer Site www professornemer

Estatístic a Prof. Edson Nemer Site: www. professornemer. com

Ementa • Introdução a Estatística • Medidas de Tendência Central • Medidas de Dispersão • Revisão de Análise Combinatória • Probabilidade • Distribuição Normal • Intervalo de Confiança

Probabilidade Introdução Além de apresentar dados e realizar cálculos nos dados obtidos, também é interessante poder fazer algum tipo de inferência. Um pesquisador que tenha anotado a idade e a pressão arterial de seus pacientes, pode montar tabelas e gráficos que descrevam como varia a pressão de seus pacientes em função da idade. Mas esse pesquisador também poderia estender suas conclusões a outros pacientes, além daqueles que ele examinou, ou seja, ele gostaria de fazer uma inferência. Para fazer inferência estatística, usam-se técnicas que exigem o conhecimento de probabilidade, embora, consciente ou inconscientemente, a probabilidade é usada por qualquer indivíduo que toma decisão em situações de incerteza.

Probabilidade A utilização das probabilidades indica a existência de um elemento de acaso, ou de incerteza, quanto à ocorrência ou não de um evento. Por exemplo, se lançarmos uma moeda para o ar, de modo geral não podemos afirmar se vai dar cada ou coroa. A probabilidade nos indicará uma medida de quão provável é a ocorrência de determinado evento. Em várias situações é desejável se ter uma medida (avaliação numérica) de quão provável é a ocorrência de determinado evento futuro: Ø Lançamento de um produto; Ø Evolução de uma doença; Ø Probabilidade de chover em um determinado período; Ø Probabilidade de um candidato vencer uma eleição;

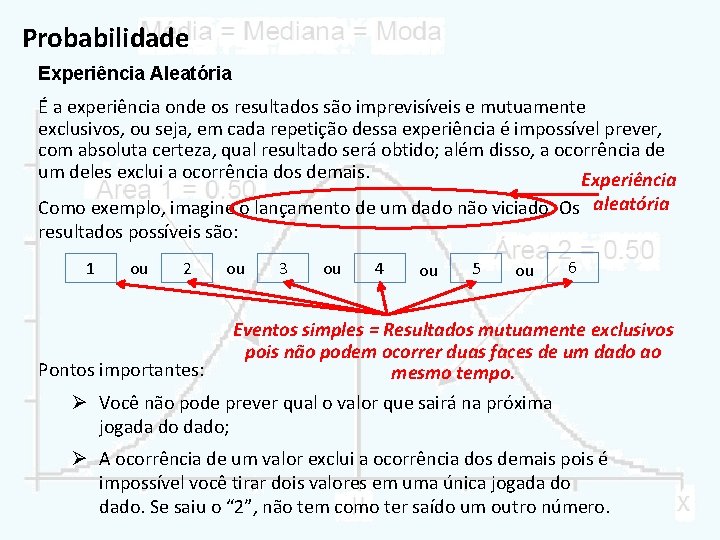
Probabilidade Experiência Aleatória É a experiência onde os resultados são imprevisíveis e mutuamente exclusivos, ou seja, em cada repetição dessa experiência é impossível prever, com absoluta certeza, qual resultado será obtido; além disso, a ocorrência de um deles exclui a ocorrência dos demais. Experiência Como exemplo, imagine o lançamento de um dado não viciado. Os aleatória resultados possíveis são: 1 ou 2 Pontos importantes: ou 3 ou 4 ou 5 ou 6 Eventos simples = Resultados mutuamente exclusivos pois não podem ocorrer duas faces de um dado ao mesmo tempo. Ø Você não pode prever qual o valor que sairá na próxima jogada do dado; Ø A ocorrência de um valor exclui a ocorrência dos demais pois é impossível você tirar dois valores em uma única jogada do dado. Se saiu o “ 2”, não tem como ter saído um outro número.

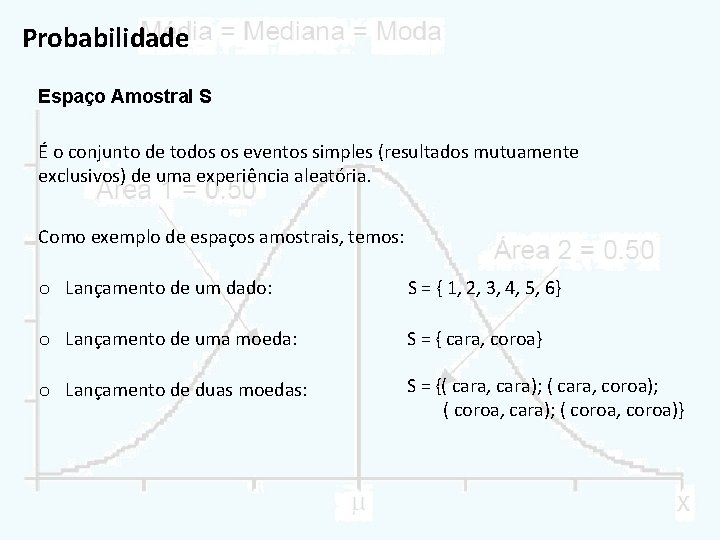
Probabilidade Espaço Amostral S É o conjunto de todos os eventos simples (resultados mutuamente exclusivos) de uma experiência aleatória. Como exemplo de espaços amostrais, temos: o Lançamento de um dado: S = { 1, 2, 3, 4, 5, 6} o Lançamento de uma moeda: S = { cara, coroa} o Lançamento de duas moedas: S = {( cara, cara); ( cara, coroa); ( coroa, cara); ( coroa, coroa)}

Probabilidade Medidas de Probabilidades Na definição clássica de probabilidade, tomamos um espaço amostral finito S={a 1, a 2, a 3, . . . , an}, no qual os pontos amostrais ai (i=1, 2, . . . , n) podem ter a mesma probabilidade de ocorrer, ou seja, são considerados equiprováveis. Então, todo subconjunto do espaço amostral diz-se um evento, sendo sua probabilidade dada por: Como exemplo, suponha um dado não viciado. Espera-se que as várias faces sejam equiprováveis, ou seja, que qualquer das faces do dado tenha a mesma probabilidade de sair quanto as outras. A probabilidade de sair o número “ 5” é: Número de casos favoráveis ao evento “ 5” é igual a 1 porque só existe um número “ 5” no dado. Número de casos possíveis é igual a 6 porque pode sair um de seis números possíveis (1, 2, 3, 4, 5 e 6)

Probabilidade Medidas de Probabilidades Para o mesmo exemplo anterior, qual seria a probabilidade de sair um número ímpar? Número de casos possíveis é igual a 6 porque pode sair um de 6 números possíveis (1, 2, 3, 4, 5 e 6) favoráveis ao evento “ímpar” é igual a 3 pois existem três faces do dado com número ímpar(1, 3 e 5). Para o mesmo exemplo anterior, qual seria a probabilidade de sair um número menor do que “ 5”? Número de casos possíveis é igual a 6 porque pode sair um de 6 números possíveis (1, 2, 3, 4, 5 e 6) Número de casos favoráveis ao evento “ímpar” é igual a 4 pois existem quatro faces do dado com número menor do que 5 (1, 2, 3 e 4).

Probabilidade Medidas de Probabilidades

Probabilidade Medidas de Probabilidades Considere mais um exemplo. Uma carta será retirada ao acaso do baralho. Qual é a probabilidade de sair um Ás? Número de casos possíveis é igual a 52 porque existem 52 cartas em um baralho. E qual é a probabilidade de sair uma figura? Número de casos possíveis é igual a 52 porque existem 52 cartas em um baralho. Número de casos favoráveis ao evento “sair Ás” é igual a 4 pois existem quatro Ases em um baralho. Número de casos favoráveis ao evento “sair figura” é igual a 12 pois existem 12 figuras em um baralho.

Probabilidade Regras Básicas da Probabilidade I. Campo de variação das probabilidades Ø A probabilidade de um evento A deve ser um número maior ou igual a 0 (zero), porém menor ou igual a 1, isto é: ou Ø Se é certo ocorrer determinado evento, a probabilidade desse evento é 1, ou 100%; Ø A probabilidade de ocorrer um número menor do que 8 no lançamento de um dado é 1 ou 100%. (evento certo) Ø Se é impossível ocorrer determinado evento, a probabilidade desse evento é 0(zero). Ø A probabilidade de ocorrer um número maior do que 8 no lançamento de um dado é 0(evento impossível).

Probabilidade Regras Básicas da Probabilidade II. Probabilidade do Espaço Amostral S Ø A probabilidade do Espaço Amostral S é igual a 1. Isto é: III. Regra da Adição de Probabilidades Ø A probabilidade de ocorrência do evento A, ou do evento B (ou de ambos) é igual a: Ø Caso os eventos A e B sejam mutuamente exclusivos, isto é: Ø Então:

Probabilidade Regras Básicas da Probabilidade =0 III. Regra da Adição de Probabilidades Ø Os eventos são mutamente exclusivos (a bola sorteada não pode ser azul e vermelha ao mesmo tempo) Exemplo: Suponha que uma urna contém duas bolas brancas, uma azul e uma vermelha. Retira-se uma bola ao acaso. Qual a probabilidade de ter saído uma bola colorida, isto é, azul ou vermelha? Ora, a probabilidade de sair bola azul é: E a probabilidade de sair bola vermelha é: Então a probabilidade de sair bola azul ou vermelha é dada pela soma:

Probabilidade Regras Básicas da Probabilidade III. Regra da Adição de Probabilidades Ø Exemplo: Imagine, agora, que uma carta será retirada ao acaso de um baralho. Qual a probabilidade de ter saído uma carta de espadas ou um Ás? Como um baralho tem 52 cartas, das quais 13 são de espadas e quatro são ases, alguém poderia pensar que a probabilidade de sair um Ás ou uma carta de espadas seria: Mas esta resposta estaria errada porque existe uma carta, o Ás de espadas, que é tanto Ás como espadas. Logo, teria sido contado duas vezes. E a resposta certa é:

Probabilidade Regras Básicas da Probabilidade IV. Probabilidade de um evento complementar Ø Exemplo: Qual a probabilidade de se retirar uma carta qualquer de um baralho, exceto copas? A probabilidade de se retirar uma carta de copas de um baralho é dada por:

Probabilidade Independência estatística Ø Dois eventos estão estatisticamente independentes se a ocorrência de um deles não afetar a ocorrência do outro. Ø Se lançarmos uma moeda por duas vezes, a probabilidade de obter uma cara no segundo lance não é afetada pelo resultado do primeiro lance. Ø Dados dois eventos independentes, A e B, a probabilidade da ocorrência conjunta é definida pela regra da multiplicação: Ø Exemplo: No lançamento de duas moedas, qual a probabilidade de sair duas caras? No caso de lançamento de duas moedas, existem quatro resultados possíveis: S = {(cara, cara), (cara, coroa), (coroa, cara), (coroa, coroa)}. Cada resultado é igualmente provável e tem probabilidade igual a ¼. Portanto, a probabilidade de sair uma sequência de duas caras é:

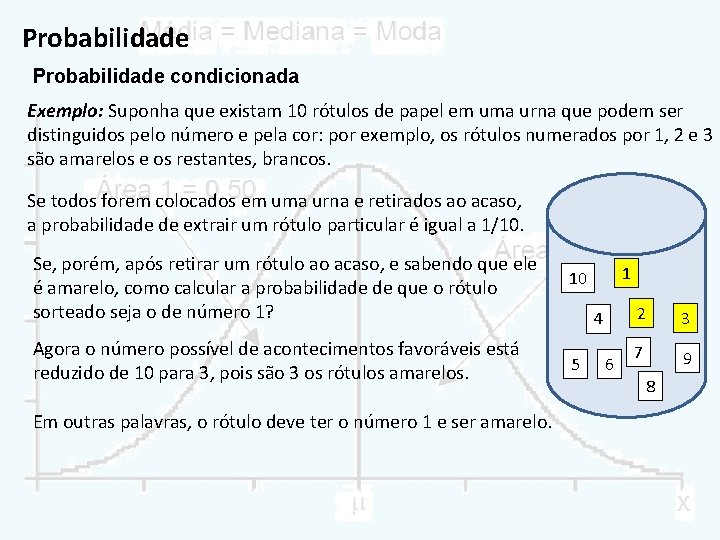
Probabilidade condicionada Ø Se a condição de independência estatística não for satisfeita, deve ser usada uma fórmula mais geral, envolvendo probabilidades condicionadas. Ø Denomina-se probabilidade condicional à probabilidade de ocorrer determinado evento sob uma dada condição. Ø Dados dois eventos, A e B, a probabilidade de que o evento B ocorra, dado que o evento A já ocorreu, é a probabilidade condicionada de B, escrita por P(B/A). Ø Da mesma forma, escrevemos a probabilidade da ocorrência de A, condicionada à ocorrência de B, como P(A/B)

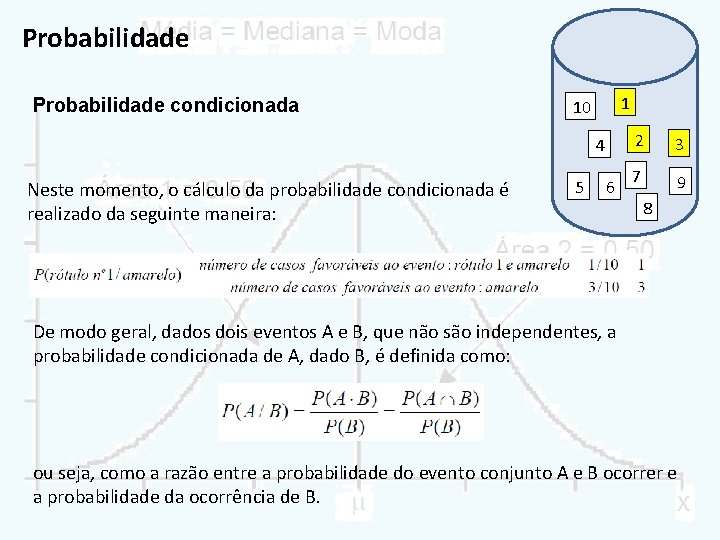
Probabilidade condicionada Exemplo: Suponha que existam 10 rótulos de papel em uma urna que podem ser distinguidos pelo número e pela cor: por exemplo, os rótulos numerados por 1, 2 e 3 são amarelos e os restantes, brancos. Se todos forem colocados em uma urna e retirados ao acaso, a probabilidade de extrair um rótulo particular é igual a 1/10. Se, porém, após retirar um rótulo ao acaso, e sabendo que ele é amarelo, como calcular a probabilidade de que o rótulo sorteado seja o de número 1? 10 Agora o número possível de acontecimentos favoráveis está reduzido de 10 para 3, pois são 3 os rótulos amarelos. 5 Em outras palavras, o rótulo deve ter o número 1 e ser amarelo. 1 4 6 2 3 7 9 8

Probabilidade condicionada 1 10 4 Neste momento, o cálculo da probabilidade condicionada é realizado da seguinte maneira: 5 6 2 3 7 9 8 De modo geral, dados dois eventos A e B, que não são independentes, a probabilidade condicionada de A, dado B, é definida como: ou seja, como a razão entre a probabilidade do evento conjunto A e B ocorrer e a probabilidade da ocorrência de B.

Probabilidade condicionada Exemplo: Suponha agora que uma carta é retirada de um baralho. Qual é a probabilidade de ser um rei preto sabendo que a carta retirada foi uma figura (valete, dama ou rei)? Sejam A ={rei preto} e B = {figura}. i) Como existem dois reis pretos no baralho, os quais são, também, figuras, tem-se que: ii) Como existem doze figuras em um baralho, tem-se que: Portanto, tem-se que:

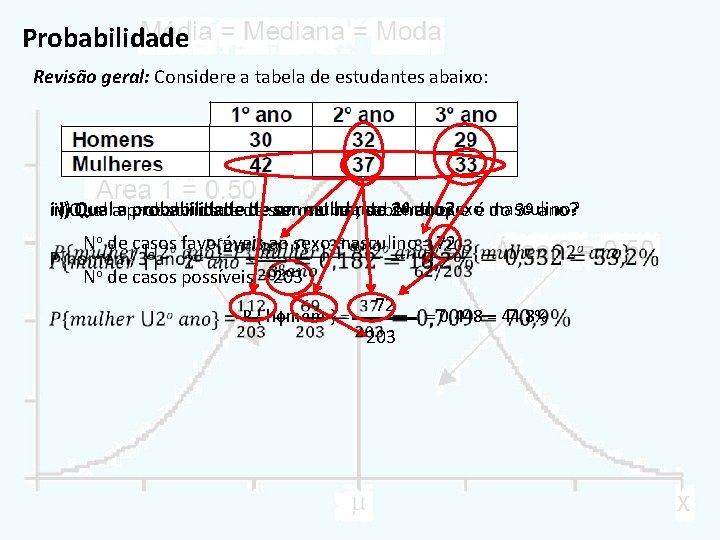
Probabilidade Revisão geral: Considere a tabela de estudantes abaixo: i)Qual ummulher, estudante doque sexoé masculino? iv) Qualaaprobabilidadede deser mulher ou ser 2º ano? iii) do ii) sabendo do 3º ano? No de casos favoráveis ao sexo masculino = 72 No de casos possíveis = 203 P { homem } = 72 203 = 0, 448 = 44, 8%