Equivalence of DFA and NFA n In this

Equivalence of DFA and NFA n In this section to convert the DFA to NFA. n Theorem: Let ‘L’ be the set accepted by a NFA then there exists a DFA that accepts the same the language ‘L’.

n n n n Proof: let M={Q, ∑, δ, q 0, F) be a NFA accepting the language ‘L’ and to define the DFA M 1={Q 1, ∑, δ 1, q 01, F 1) The final states of ‘M 1’are equal to the subsets of states of ‘M’. Q 1=2 Q. Q has a finite set of states. i. e Q={q 1, q 2…qn} Q 1 has finite set of states accepted by a DFA. Q={q 1, q 2. q 3…. qi} Q 1=[q 1, q 2, q 3…. qi]

i. e equivalent to the single state of DFA corresponds to the set of states in NFA. n δ 1= ([q 1, q 2…qi], a) = [p 1, p 2…pi] if and only if δ = ({q 1, q 2…qi}, a) = {p 1, p 2…pi} It is easy to show by an induction method on the length of the string ‘x’ δ 1(q 01, x) = [q 1, q 2…qi] if and only if δ = ({q 1, q 2…qi}, a) = {p 1, p 2…pi} n

n n n Basis step: The result id trivial for |x|=0 Induction step: suppose length of the string should be length M or less. δ 1(q 01, xa) = δ 1(q 01, x), a) By inductive hypothesis of δ 1(q 01, x) = [p 1, p 2…pi] if and only if δ(q 0, x) = {p 1, p 2…pi}

n n δ 1([p 1, p 2…pi], a) = [r 1, r 2…rk] If and only if δ({p 1, p 2…pi}, a) = {r 1, r 2…. rk} To complete the proof we have only to add that δ 1(q 01, x) is in final state F 1. Hence theorem is proved. i. e L(M) =L(M 1).

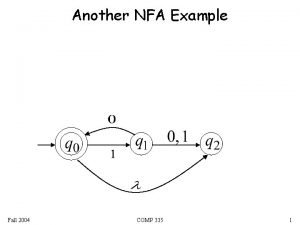
problem 1 n Construct a DFA from an NFA 0 q 0 *q 1 1 {q 0, q 1} {q 1} Ø {q 0, q 1}

n n n n n To construct a DFA M 1={q 1, ∑, δ 1, q 01, F 1) and accepting the language L(M 1). Q 1=2 Q. Q=2 22=4 δ 1( Ø, 0) =Ø. δ 1( Ø, 1) =Ø. δ 1( q 0, 0) =[q 0 q 1]. δ 1( q 0, 1) =[q 1]. δ 1( q 1, 0) =Ø. δ 1( q 1, 1) =[q 0 q 1] δ 1( [q 0 q 1], 0) =δ{q 0 q 1}, 0) =δ( q 0, 0) U δ( q 1, 0) ={q 0 q 1} U Ø => [q 0 q 1]

n δ 1( [q 0 q 1], 1) =δ{q 0 q 1}, 1) =δ( q 0, 1) U δ( q 1, 1) ={q 0 q 1} U {q 0 q 1} => [q 0 q 1] Set of final states {[q 1], [q 0 q 1]}

solution 0 Ø [q 0] [q 1] [q 0 q 1] 1 Ø [q 0 q 1] [q 0 q 1]

Problem 2 n Construct a DFA from an NFA 0 1 p {p, q} {p} q {r} r {s} Ø *s {s}

n n n n To construct a DFA M 1={q 1, ∑, δ 1, q 01, F 1) and accepting the language L(M 1). Q 1=2 Q. Q=4 24=16. δ 1( Ø, 0) =Ø. δ 1( Ø, 1) =Ø. δ 1( p, 0) =[pq]. δ 1( p, 1) =[p]. δ 1( q, 0) =[r]. δ 1( q, 1) =[r] δ 1( r, 0) = [s] δ 1( r, 1) = Ø δ 1( s, 0) = [s] δ 1( s, 1) = [s]

n n n n δ 1( [qs], 1) = [rs] δ 1( [rs], 0) = [s] δ 1( [rs], 1) = [s] δ 1( [pqr], 0) = [pqrs] δ 1( [pqr], 1) = [pr] δ 1( [pqs], 0) = [pqrs] δ 1( [pqs], 1) = [prs] δ 1( [prs], 0) = [pqs] δ 1( [prs], 1) = [ps] δ 1( [qrs], 0) = [rs] δ 1( [qrs], 1) = [rs] δ 1( [pqrs], 0) = [pqrs] δ 1( [pqrs], 1) = [prs] Set of finite states { [s], [ps], [rs], [pqs], [prs], [pqrs], [qrs]}

problem 3 n Construct a DFA from an NFA 0 1 p {q, s} {q} q {r} {q, r} r {s} {p} *s Ø {p}

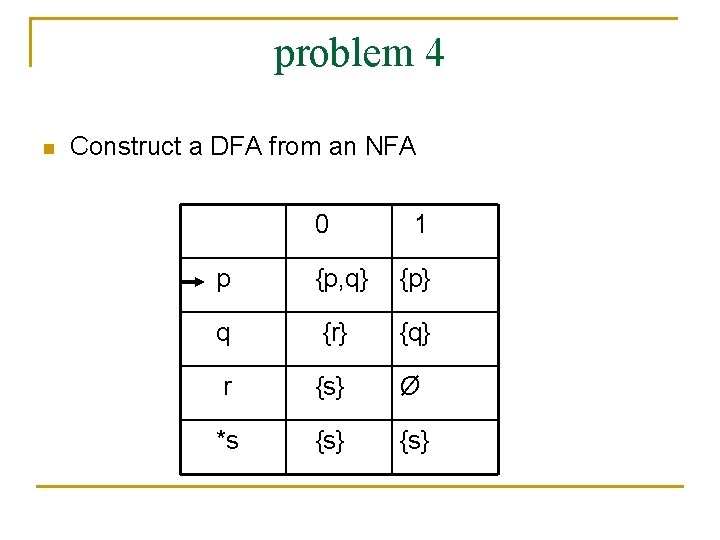
problem 4 n Construct a DFA from an NFA 0 1 p {p, q} {p} q {r} {q} r {s} Ø *s {s}

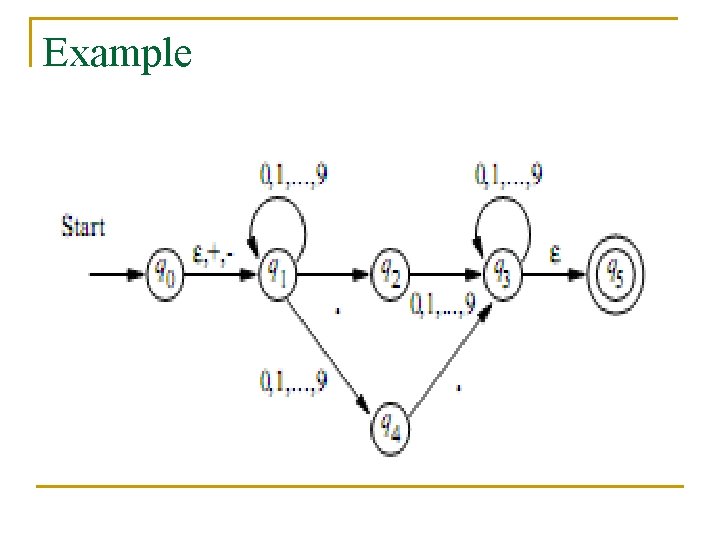
Finite Automata with є-closure n n We shall introduce the another extension of FA. NFA is allowed to make a transition with spontaneously without receiving or reading many input symbols.

Contd. .

Example

Transition table

Finite Automata with є-closure

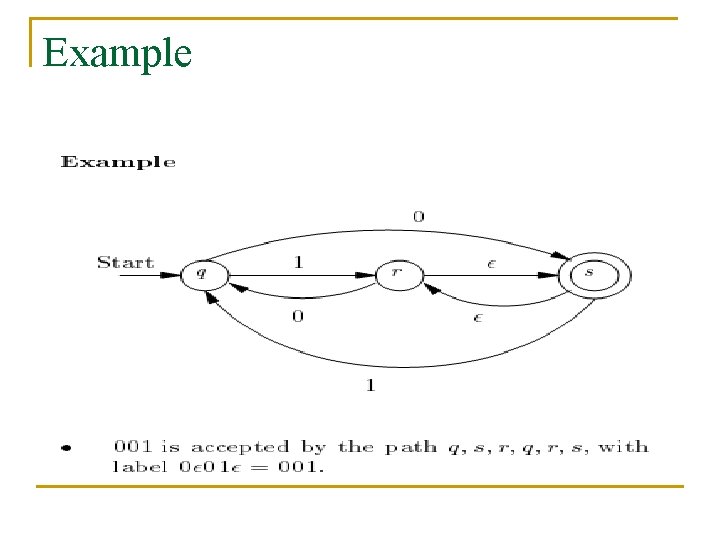
Example

Formal definition of NFA - є closure. n To represent the ∑with NFA A={Q, ∑, δ, q 0, F) where all components have a same interpretations as for a NFA. q q A state in Q. A members of Є U {є} either an input symbol is empty or a set of strings.

E-closure : Definition

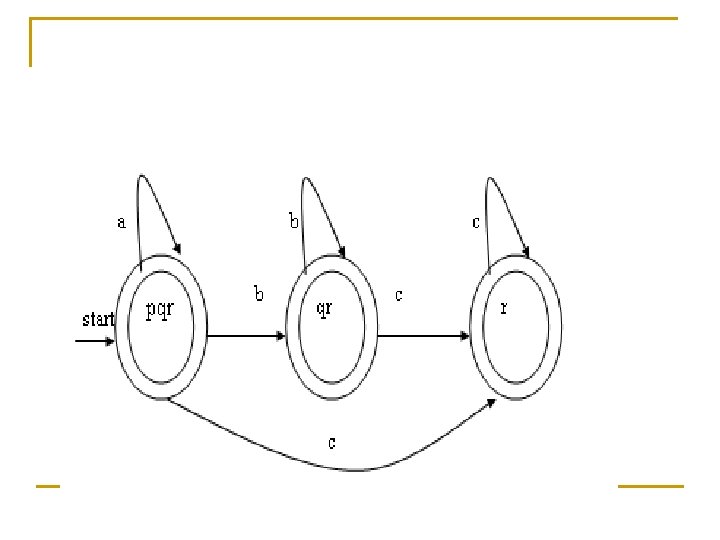
Example: Find the є-closure for all the states of given figure

solution n n n ECLOSE(1) ={1, 2, 3, 4, 6} ECLOSE(2) ={2, 3, 6} ECLOSE(3) ={3, 6} ECLOSE(4) ={4} ECLOSE(5) ={5} ECLOSE(6) ={6} ECLOSE(7) ={7}

Inductive definition on δ

Problem 1: consider the following epsilon with NFA and compute the empty closure of each states and find its equivalent to the DFA. є a b c p {q} {p} Ø Ø q {r} Ø {q} Ø *r Ø Ø Ø {r}

n n n n Let A be a NFA with є-closure which has A={Q, ∑, δ, q 0, F) Q={p, q. r} ∑ = {є, a, b, c} To find ECLOSE for all states. ECLOSE(p) = {p, q, r} ECLOSE(q) = {q, r} ECLOSE(r) = {r}

Problem 2: consider the following epsilon with NFA and compute the empty closure of each states and find its equivalent to the DFA. є a b c p Ø {p} {q} {r} q {p} {q} {r} Ø *r {q} {r} Ø {p}

Problem 3: consider the following epsilon with NFA and compute the empty closure of each states and find its equivalent to the DFA. є a b c p {q, r} Ø {q} {r} q Ø {p} {r} {p, q} *r Ø Ø