SEMESTER PENDEK 20152016 OTOMATA DAN TEORI BAHASA FORMAL

SEMESTER PENDEK 2015/2016 OTOMATA DAN TEORI BAHASA FORMAL Betha Nurina Sari, M. Kom

PERTEMUAN 4 q Ekuivalensi Non DFA ke DFA q Non DFA dengan -move

Ekuivalensi NFA → DFA Dari sebuah mesin Non-deterministic Finite Automata (NFA) dapat dibuat mesin Deterministic Finite Automata (DFA)-nya yang ekuivalen (bersesuaian). Ekuivalen disini artinya mampu menerima bahasa yang sama.

Ekuivalensi Non DFA ke DFA Definisi üSimulasi algoritma üTahap Pengubahan üContoh soal ü

Ekivalensi DFA dan NFA : Suatu DFA dapat dipandang sebagai kasus khusus (subset) dari NFA. Jelas bahwa kelas bahasa yang diterima oleh DFA juga akan diterima oleh NFA Namun ternyata DFA juga dapat mensimulasikan NFA; yaitu untuk setiap NFA kita dapat membuat DFA yang ekivalen. Dapat dibuktikan bahwa DFA dan NFA adalah ekivalen, sehingga dapat disebut FA saja.
Simulasi NFA oleh DFA : Cara simulasi NFA oleh DFA adalah dengan membuat state DFA berkorespondensi dengan set state di NFA DFA yang dibentuk mencatat semua state yang mungkin pada NFA setelah membaca input tertentu

Algoritma 1. Buat semua state yang merupakan subset dari state semula. jumlah state menjadi 2 Q 2. Telusuri transisi state–state yang baru terbentuk, dari diagram transisi. 3. Tentukan state awal : {q 0} 4. Tentukan state akhir adalah state yang elemennya mengandung state akhir. 5. Reduksi state yang tak tercapai oleh state awal.
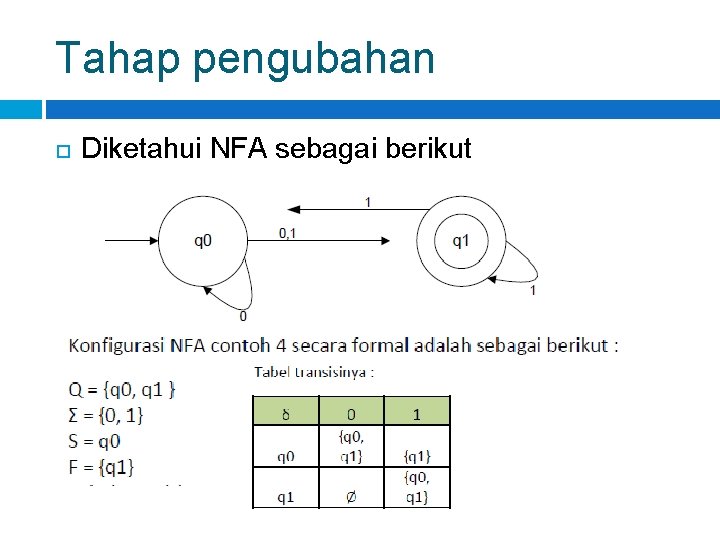
Tahap pengubahan Diketahui NFA sebagai berikut
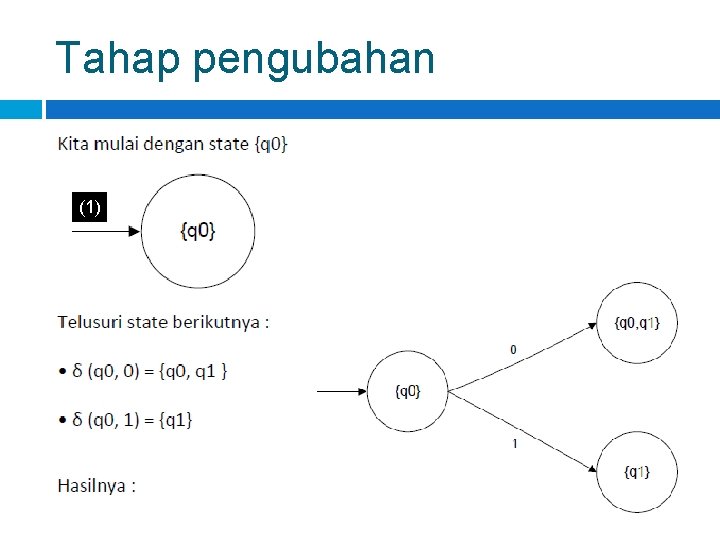
Tahap pengubahan (1)

Tahap pengubahan
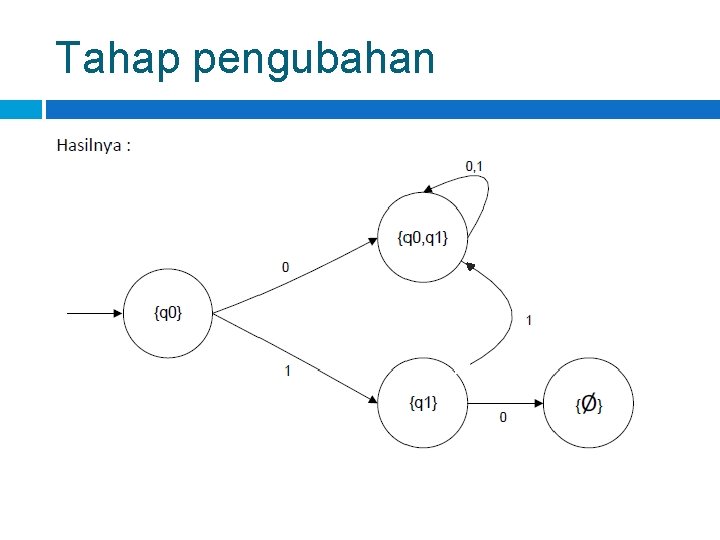
Tahap pengubahan
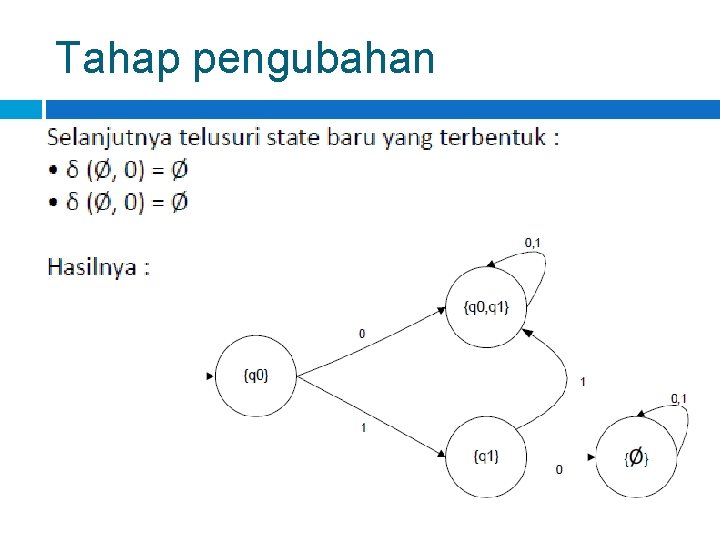
Tahap pengubahan
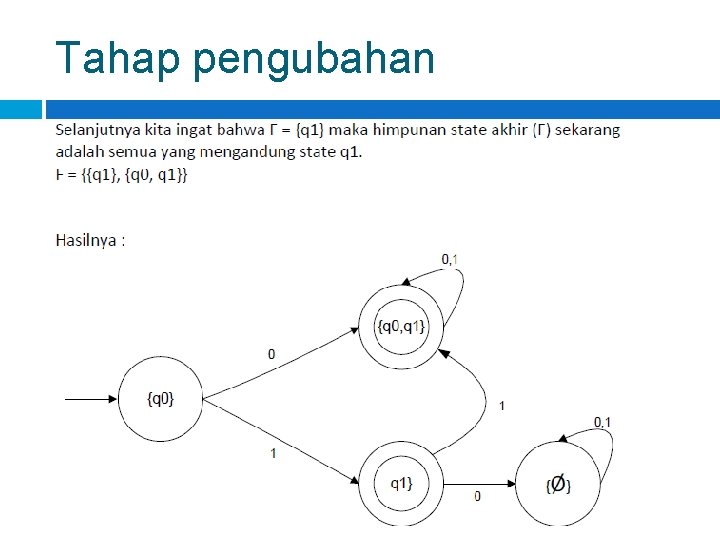
Tahap pengubahan
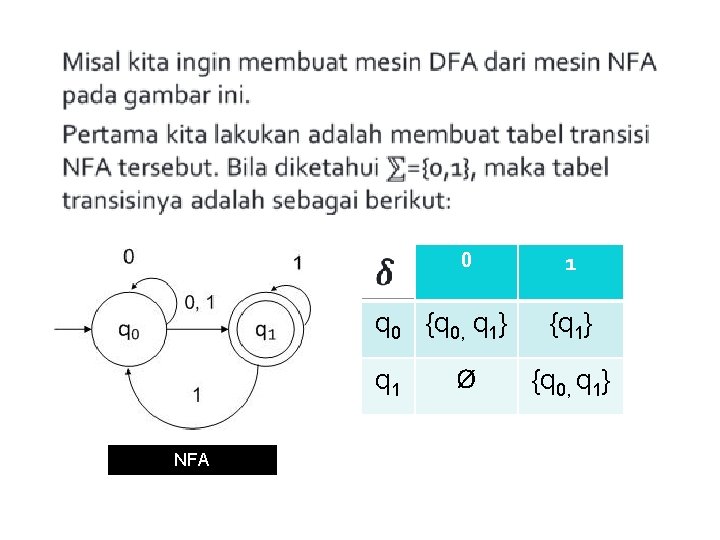
0 q 0 {q 0, q 1} q 1 NFA Ø 1 {q 1} {q 0, q 1}
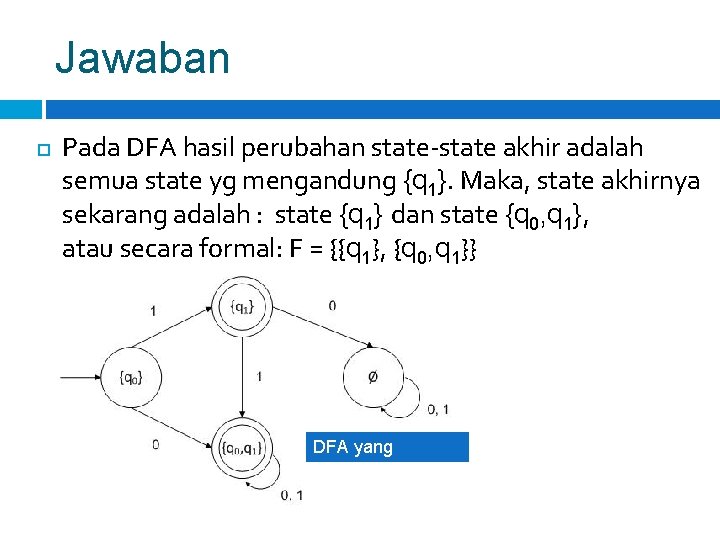
Jawaban Pada DFA hasil perubahan state-state akhir adalah semua state yg mengandung {q 1}. Maka, state akhirnya sekarang adalah : state {q 1} dan state {q 0, q 1}, atau secara formal: F = {{q 1}, {q 0, q 1}} DFA yang ekuivalen
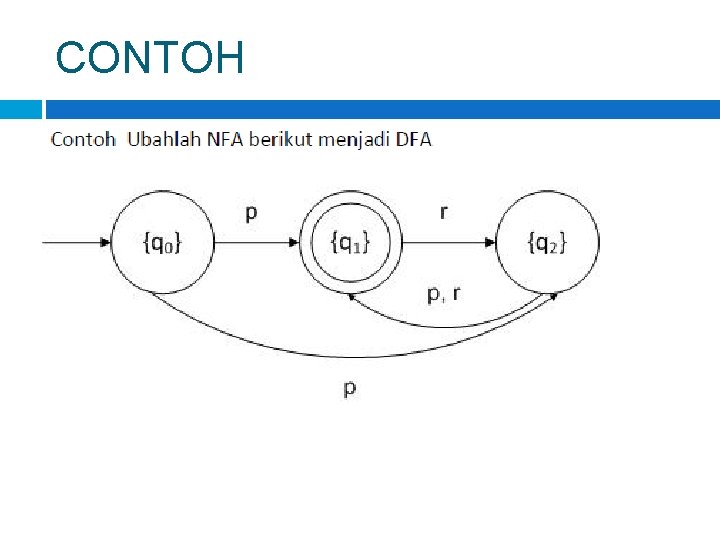
CONTOH
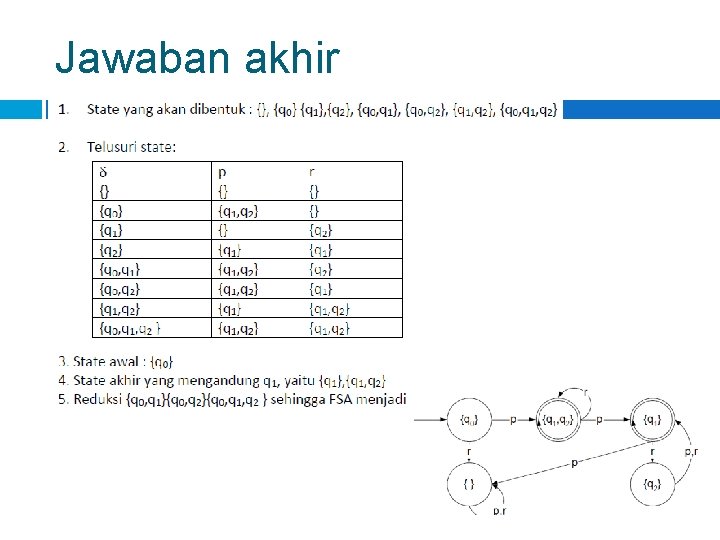
Jawaban akhir

Non DFA dengan -move - Definisi - Contoh
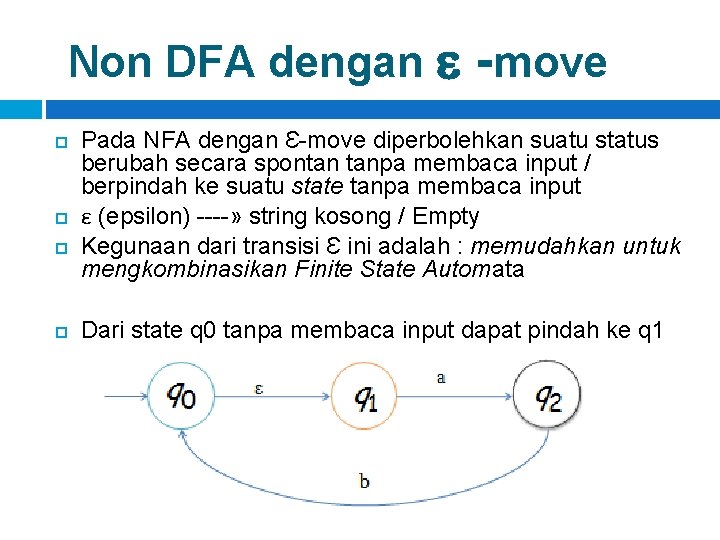
Non DFA dengan -move Pada NFA dengan Ԑ-move diperbolehkan suatu status berubah secara spontan tanpa membaca input / berpindah ke suatu state tanpa membaca input ε (epsilon) ----» string kosong / Empty Kegunaan dari transisi Ԑ ini adalah : memudahkan untuk mengkombinasikan Finite State Automata Dari state q 0 tanpa membaca input dapat pindah ke q 1
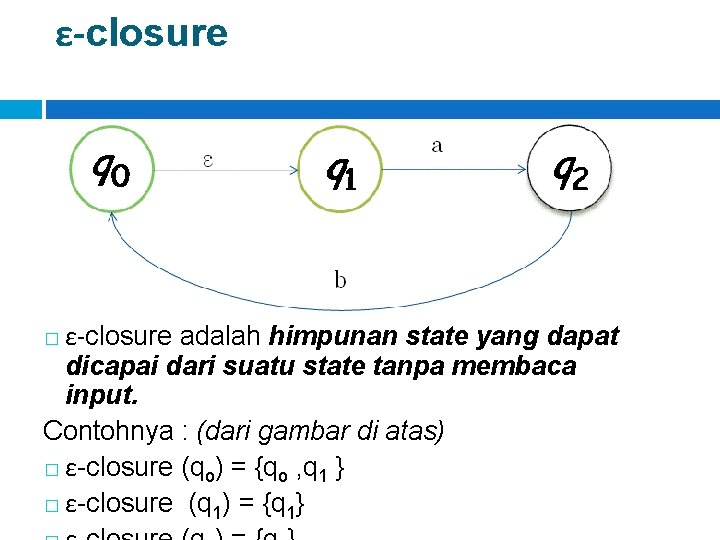
ε-closure adalah himpunan state yang dapat dicapai dari suatu state tanpa membaca input. Contohnya : (dari gambar di atas) � ε-closure (qo) = {qo , q 1 } � ε-closure (q 1) = {q 1} �

Ekuivalensi NFA dengan ε-move ke NFA tanpa ε-move Buat tabel transisi NFA dengan ε-move • Tentukan ε-closure setiap state • Carilah fungsi transisi /tabel transisi yang baru (δ’), rumus : δ’(state, input)=ε-closure(δ(εclosure(state), input)) • Tentukan state akhirnya: • State-state akhir semula ditambah dengan state yang ε-closure nya menuju ke salah satu dari state akhir semula, rumusnya : F’ = F ∪ {q |ε-closure(q) ( ∩ F ≠ ∅} •
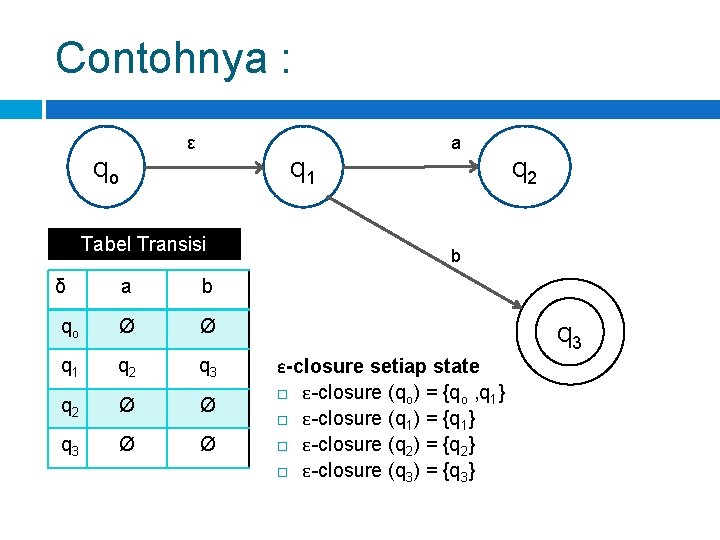
Contohnya : ε qo q 1 Tabel Transisi δ a b qo Ø Ø q 1 q 2 q 3 q 2 Ø Ø q 3 Ø Ø a q 2 b q 3 ε-closure setiap state ε-closure (qo) = {qo , q 1} ε-closure (q 1) = {q 1} ε-closure (q 2) = {q 2} ε-closure (q 3) = {q 3}

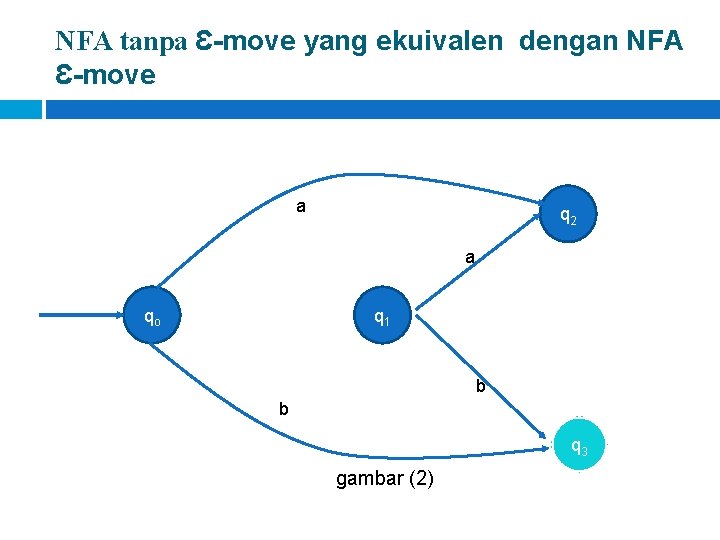
NFA tanpa Ԑ-move yang ekuivalen dengan NFA Ԑ-move a q 2 a qo q 1 b b q 3 gambar (2)

NEXT >> UTS : Bahan pertemuan 1 -3 Sifat Open Note : buat note di 1 lembar A 4 (tulis tangan/printed)
- Slides: 25