PERTEMUAN 3 EKIVALENSI NFA KE DFA Tahapan Pengubahan

PERTEMUAN 3 EKIVALENSI NFA KE DFA

Tahapan Pengubahan Non-Deterministic Finite Automata ke Deterministic Finite Automata Dari sebuah mesin Non-Deterministic Finite Automata dapat dibuat mesin DFA yang ekivalen. Ekivalen artinya mampu menerima bahasa yang sama. * Suatu DFA dapat dipandang sebagai kasus khusus (subset) dari NFA. • Jelas bahwa kelas bahasa yang diterima oleh DFA juga akan diterima oleh DFA • Namun ternyata DFA juga dapat mensimulasikan NFA; yaitu untuk setiap NFA kita dapat membuat DFA yang ekivalen • Dapat dibuktikan bahwa DFA dan NFA adalah ekivalen, sehingga dapat disebut FA saja Simulasi NFA oleh DFA • Cara simulasi NFA oleh DFA adalah dengan membuat state DFA berkorespondensi dengan set state di NFA • DFA yang dibentuk mencatat semua state yang mungkin pada NFA setelah membaca input tertentu

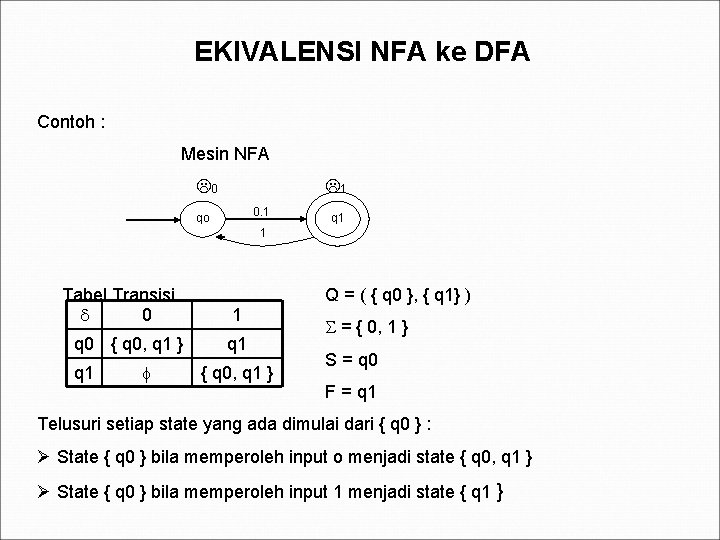
EKIVALENSI NFA ke DFA Contoh : Mesin NFA 0 1 0. 1 qo q 1 1 Tabel Transisi 0 q 0 { q 0, q 1 } q 1 Q = ( { q 0 }, { q 1} ) 1 q 1 { q 0, q 1 } = { 0, 1 } S = q 0 F = q 1 Telusuri setiap state yang ada dimulai dari { q 0 } : Ø State { q 0 } bila memperoleh input o menjadi state { q 0, q 1 } Ø State { q 0 } bila memperoleh input 1 menjadi state { q 1 }

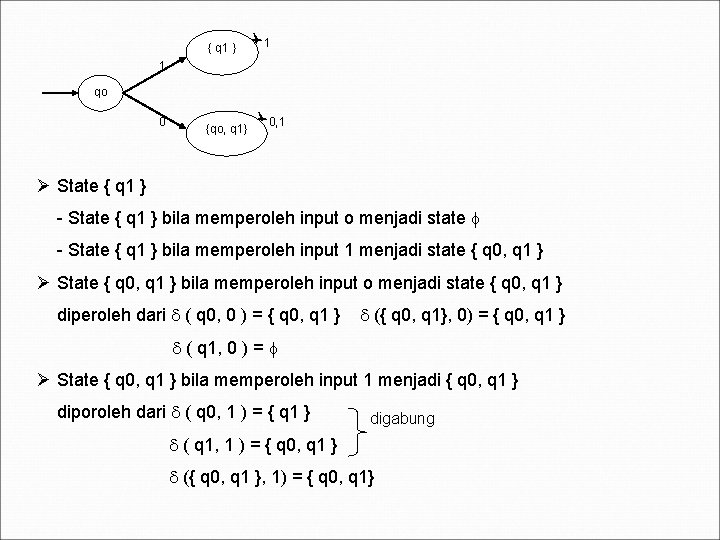
{ q 1 } 1 1 qo 0 {qo, q 1} 0, 1 Ø State { q 1 } - State { q 1 } bila memperoleh input o menjadi state - State { q 1 } bila memperoleh input 1 menjadi state { q 0, q 1 } Ø State { q 0, q 1 } bila memperoleh input o menjadi state { q 0, q 1 } diperoleh dari ( q 0, 0 ) = { q 0, q 1 } ({ q 0, q 1}, 0) = { q 0, q 1 } ( q 1, 0 ) = Ø State { q 0, q 1 } bila memperoleh input 1 menjadi { q 0, q 1 } diporoleh dari ( q 0, 1 ) = { q 1 } digabung ( q 1, 1 ) = { q 0, q 1 } ({ q 0, q 1 }, 1) = { q 0, q 1}

Hasil setelah penelusuran { q 1 }, { q 0, q 1 } q 1 1 0 1 qo 0, 1 ( , 0 ) = ( , 1 ) = 0 F = ({ q 1 }, { q 0, q 1 }) { q 0, q 1 } 0. 1 Hasilnya adalah mesin DFA Tabel Transisi Konfigurasi Mesin Q = ( qo, { q 0, q 1 }, q 1, ) 0 1 q 0 { q 0, q 1 } q 1 { q 0, q 1 } S = q 0 { q 0, q 1 } F = ( q 1, { q 0, q 1 } ) { q 0, q 1 } ∑ = { 1, 0 }

Tugas 1. Buatlah DFA yang ekuivalen dengan NFA berikut Q = { p, q, r, s} ∑ = { 0, 1} S=p F = {s} Fungsi transisinya dinyatakan dalam tabel transisi berikut 0 1 p p, q p q r r r s - s s s

2. Buatlah DFA yang ekuivalen dengan NFA berikut Q = { p, q, r, s} ∑ = { 0, 1} S=p F = {q, s} Fungsi transisinya dinyatakan dalam tabel transisi berikut 0 1 p p, s p q r q, r r s p s - p

Soal 1. Dari sebuah mesin Non-Deterministic Finite Automata dapat dibuat mesin DFA yang ekivalen. Ekivalen artinya … a. mampu menerima bahasa yang sama b. mampu menerima bahasa yang berbeda c. mampu menolak input d. mampu menolak output e. mampu menerjemahkan bahasa 2. Di bawah ini yang merupakan pernyataan benar tentang simulasi NFA oleh DFA a. Cara simulasi NFA oleh DFA adalah dengan membuat state DFA berkorespondensi dengan set state di NFA b. DFA yang dibentuk mencatat semua state yang mungkin pada NFA setelah membaca output tertentu c. DFA yang dibentuk mencatat semua mesin yang mungkin pada NFA setelah membaca output tertentu d. Cara simulasi NFA oleh DFA adalah dengan membuat state DFA berkorespondensi dengan mesin turing e. Cara simulasi NFA oleh DFA adalah dengan membuat mesin turing berkorespondensi dengan set state di NFA

Soal 2. Di bawah ini yang merupakan pernyataan benar tentang simulasi NFA oleh DFA a. Cara simulasi NFA oleh DFA adalah dengan membuat state DFA berkorespondensi dengan set state di NFA b. DFA yang dibentuk mencatat semua state yang mungkin pada NFA setelah membaca output tertentu c. DFA yang dibentuk mencatat semua mesin yang mungkin pada NFA setelah membaca output tertentu d. Cara simulasi NFA oleh DFA adalah dengan membuat state DFA berkorespondensi dengan mesin turing e. Cara simulasi NFA oleh DFA adalah dengan membuat mesin turing berkorespondensi dengan set state di NFA 3. Jika ingin membuat mesin DFA dari mesin NFA, langkah pertama yang kita lakukan adalah. . . a. Membuat tabel transisi b. Membuat tabel logika kebenaran c. Membuat mesin turing d. Membuat himpunan state e. Berkorespondensi dengan mesin NFA

3. Jika ingin membuat mesin DFA dari mesin NFA, langkah pertama yang kita lakukan adalah. . . a. Membuat tabel transisi b. Membuat tabel logika kebenaran c. Membuat mesin turing d. Membuat himpunan state e. Berkorespondensi dengan mesin NFA 4. Dari gambar di atas , state yang akan dibentuk atalah … a. { }, {q 0}, {q 1}, {q 0, q 1} b. { }, {0, 1} c. {q 0}, {q 1} d. {0}, {0, 1}, {1} e. {q 0}, {q 1}, {0, 1}, {1}

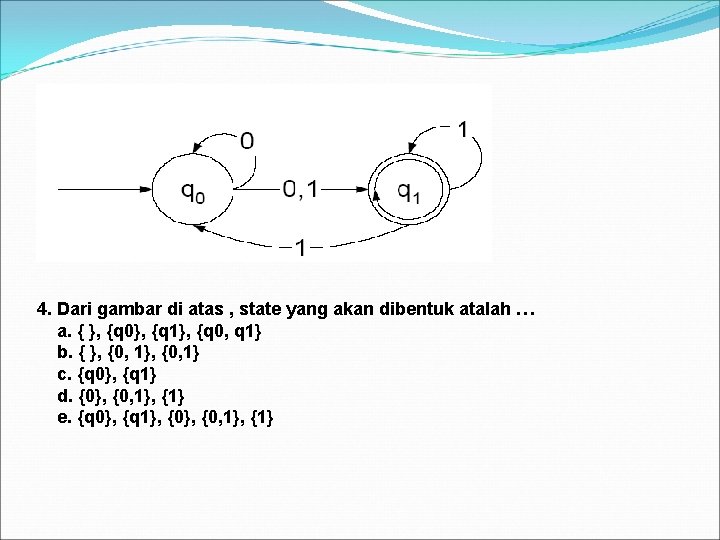
4. Dari gambar di atas , state yang akan dibentuk atalah … a. { }, {q 0}, {q 1}, {q 0, q 1} b. { }, {0, 1} c. {q 0}, {q 1} d. {0}, {0, 1}, {1} e. {q 0}, {q 1}, {0, 1}, {1}

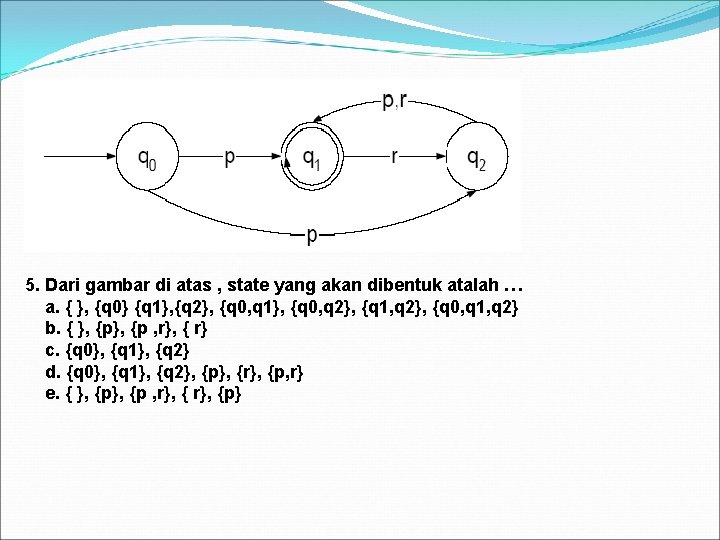
5. Dari gambar di atas , state yang akan dibentuk atalah … a. { }, {q 0} {q 1}, {q 2}, {q 0, q 1}, {q 0, q 2}, {q 1, q 2}, {q 0, q 1, q 2} b. { }, {p , r}, { r} c. {q 0}, {q 1}, {q 2} d. {q 0}, {q 1}, {q 2}, {p}, {r}, {p, r} e. { }, {p , r}, {p}