Lecture 7 From NFA to DFA DFA For

Lecture 7 From NFA to DFA

DFA • For every string x, there is a unique path from initial state and associated with x. x x is accepted if and only if this path ends at a final state.

NFA • For any string x, there may exist none or more than one path from initial state and associated with x.

NFA DFA • Consider an NFA M=(Q, Σ, δ, s, F). • For x in Σ*, define [x] = {q in Q | there exists a path s x • Define DFA M’=(Q’, Σ, δ’, s’, F’}: Q’ = { [x] | x in Σ* }, δ ([x], a) = [xa] for x in Σ* and a in Σ, s’ = [ε], F’ = { [x] | x in L(M) } q}

Construction of M’ Special Case: M has no ε-move. • [ε] = {s} • Suppose [x] is known. How to get [xa] for a in Σ?

From [x] to [xa] • [xa] = { p | there exists a path q some q in [x] } = { p | there exists q in [x], a q edgep } = U δ(q, a) q in [x] a p for path

Construction of M’ • F’ = {[x] | x in L(M)} = {[x] | [x] ∩ F ≠ Ǿ }

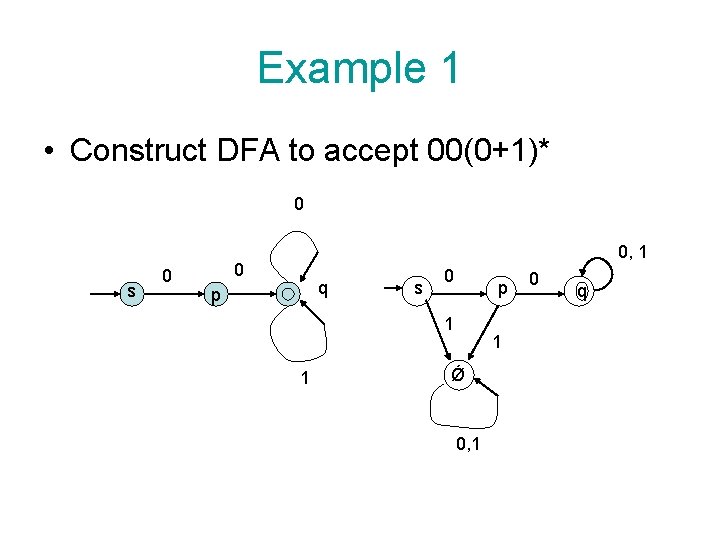
Example 1 • Construct DFA to accept 00(0+1)* 0 s 0 0, 1 0 q p s 0 p 1 1 1 Ǿ 0, 1 0 q

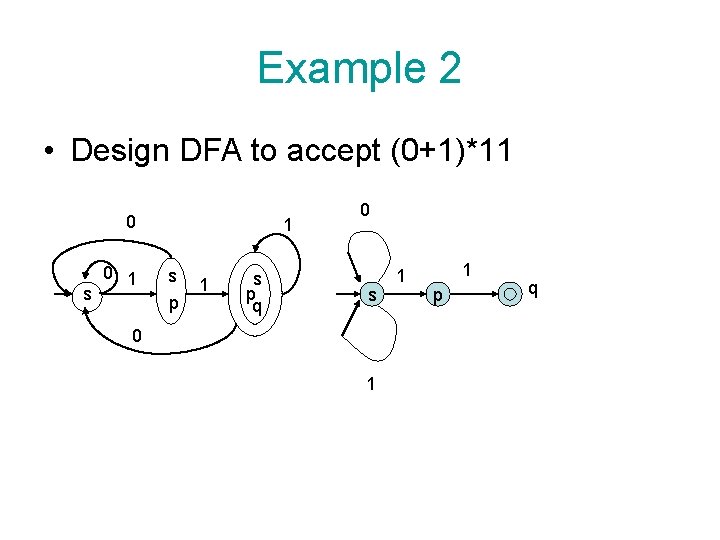
Example 2 • Design DFA to accept (0+1)*11 0 s 0 1 1 s p q 0 s 0 1 1 1 p q

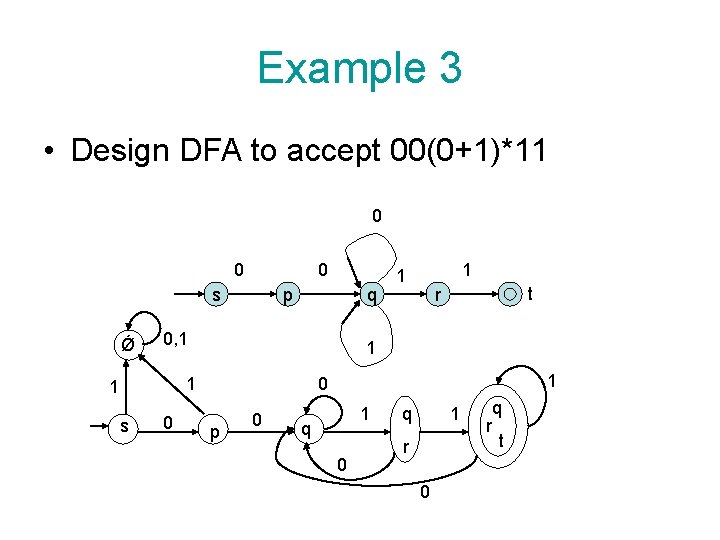
Example 3 • Design DFA to accept 00(0+1)*11 0 0 0 s Ǿ p q 0, 1 s 0 t r 1 1 1 0 p 0 1 q 0 q 1 r 0 r q t

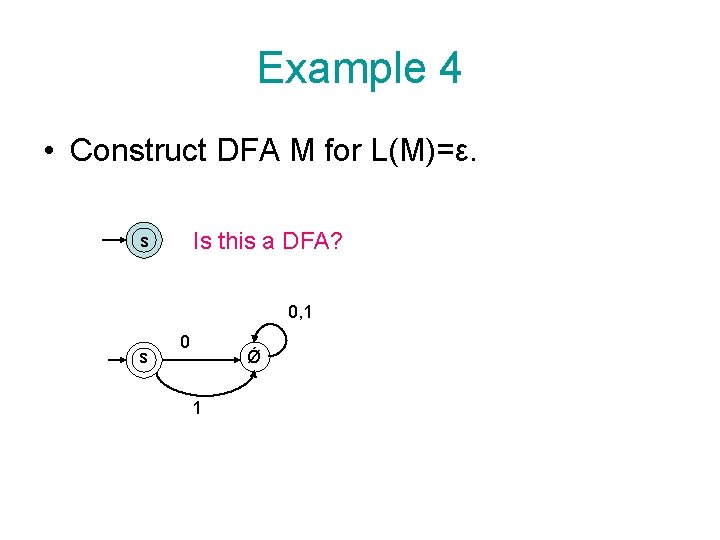
Example 4 • Construct DFA M for L(M)=ε. Is this a DFA? s 0, 1 s 0 Ǿ 1

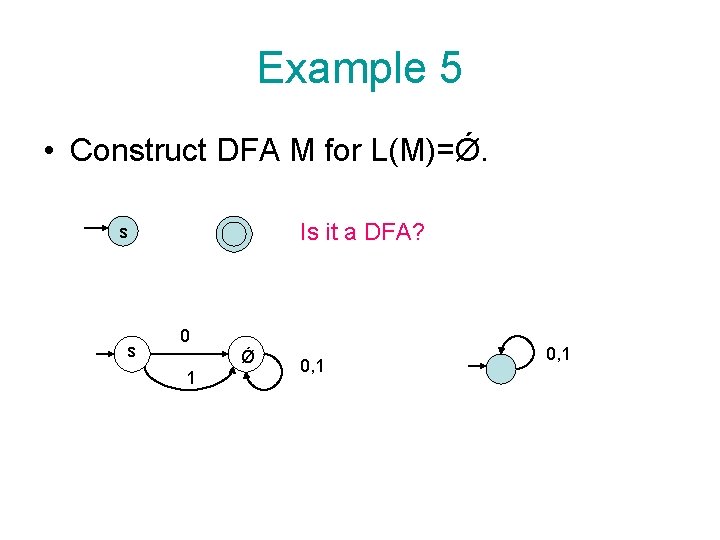
Example 5 • Construct DFA M for L(M)=Ǿ. Is it a DFA? s s 0 Ǿ 1 0, 1

Construction of M’ • For q in Q, define ε ε-closure(q) = {p | there exists a path q pathp} ε • [ε] = {q | there is a path s q} path = ε-closure(s) • Suppose [x] is known. How to get [xa] for a in Σ?

From [x] to [xa] a • [xa] = { p | there exists a path q pathp for some q in [x] } = { p | there exists q in [x], a ε q edger pathp } = { p | for some q in [x] and r in δ(q, a), p in ε-closure(r) } = Uq in [x]U r in δ(q, a) ε-closure(r)

Construction of M’ • F’ = {[x] | x in L(M)} = {[x] | [x] ∩ F ≠ Ǿ }

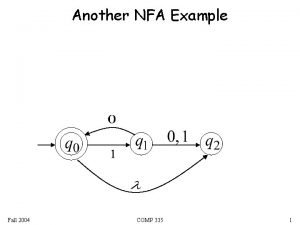
Example 6 • Construct DFA M for L(M)=(0+1)*. 0, 1 ε ε s p q 0, 1 s p q 0 1 p q 0, 1

Example 7 • Convert the following NFA to DFA. 0 s ε 0 p 1 0 q 1 ε ε 0 s r p r 1 0 q, r, p 1 q r s p 0 1 0

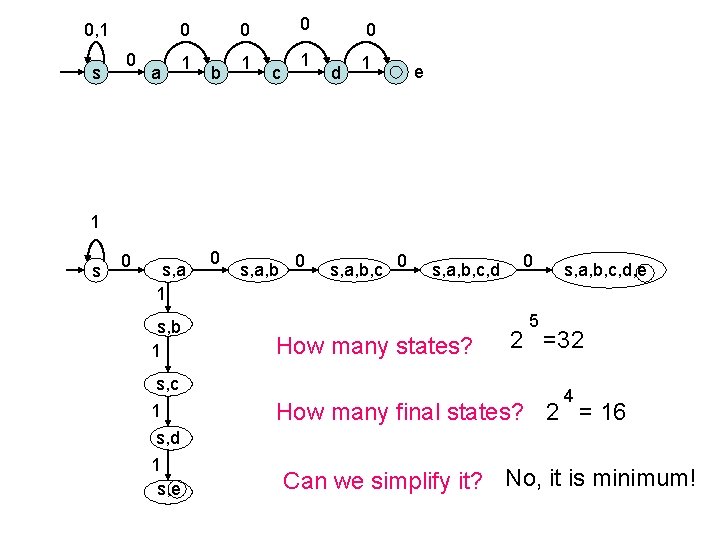
0, 1 s 0 0 a 1 0 0 b 1 c 1 0 d 1 e 1 s 0 s, a 1 s, b 1 s, c 1 s, d 1 s, e 0 s, a, b, c, d, e 5 How many states? 2 =32 4 How many final states? 2 = 16 Can we simplify it? No, it is minimum!