Lecture 3 DFA vs NFA properties of RL

Lecture 3 DFA vs. NFA, properties of RL 2004 SDU

Regular operations They are used to study the properties of regular languages. Let A and B be languages, define the regular operations union, concatenation, and star as follows: • Union: A B = {x| x A or x B} • Concatenation: A B = {xy | x A and y B} • Star: A* = {x 1 x 2…xk | k 0 and each xi A } Example: A = {good, bad}, B = {boy, girl} Then A B = {good, bad, boy, girl}; A B ={goodboy, goodgirl, badboy, badgirl}, and A*={ , good, bad, good, goodbad, badgood, badbad, goodgood, goodbad, goodbadgood, goodbadbad, …} 2004 SDU 2

Closure properties of Regular Languages Regular languages are closed under: § Union if A and B are regular languages, so is A B § Concatenation if A and B are regular languages, so is A B § Star * if A is a regular language, so is A*. 2004 SDU 3

General Construction for and Let A 1 and A 2 be two regular languages, and M 1 and M 2 be the DFAs that recognize them, we want to construct a DFA M to recognize A 1 A 2. Can M first simulate M 1 and then simulate M 2 on an given input? Idea: Simulate two DFA's simultaneously. Let M 1 = (Q 1, , 1, s 1, F 1) and M 2 = (Q 2, , 2, s 2, F 2) Define: M = (Q, , , s, F) where: § Q = Q 1 Q 2 § s = (s 1, s 2) § ((q 1, q 2), ) = ( 1(q 1, ), 2(q 2, )), for each (q 1, q 2) Q, and each For Union, F = ? The proof? § Ans: (Q 1 F 2) (F 1 Q 2) For Intersection, F = ? The proof? § Ans: F 1 F 2 2004 SDU 4

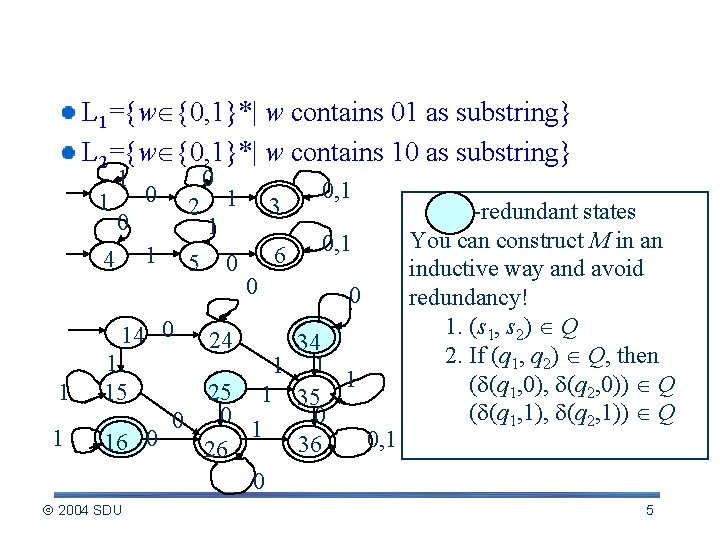
Example of union L 1={w {0, 1}*| w contains 01 as substring} L 2={w {0, 1}*| w contains 10 as substring} 1 1 0 0 1 4 14 0 1 1 0 2 5 1 3 0 6 1 24 0 0, 1 0 34 1 1 15 25 1 35 0 0 0 1 0, 1 16 0 36 26 0 2004 SDU -redundant states You can construct M in an inductive way and avoid redundancy! 1. (s 1, s 2) Q 2. If (q 1, q 2) Q, then ( (q 1, 0), (q 2, 0)) Q ( (q 1, 1), (q 2, 1)) Q 5

How about the other regular operations The concatenation ? The star * ? Can we use similar way? To solve this problem, we introduce a new technique non-determinism. § In deterministic computation, the next state is determined § In non-deterministic computation, several choices may exist § Page 48 for example, and 49 for clarity 2004 SDU 6

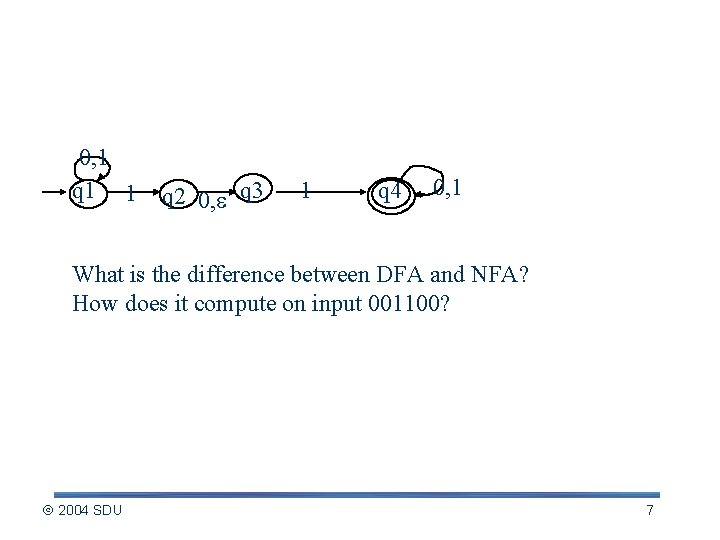
An example of NFA 0, 1 q 1 1 q 2 0, q 3 1 q 4 0, 1 What is the difference between DFA and NFA? How does it compute on input 001100? 2004 SDU 7

Formal definition of DFA A DFA is a 5 -tuple: M = (Q, , , s, F) Where, § § Q is finite set of states is finite input alphabet s Q is the initial state F Q is the set of final states § : Q -> Q // note that this is a function 2004 SDU 8

Nondeterministic Finite Automaton (NFA) Generalization of DFA. Allows: § 0 or more next states for the same (q, a). – Guessing § Transitions labeled by the empty string . – Changing state without reading input Motivation: Flexibility, simplicity. 2004 SDU 9

Formal definition of NFA Notation: = { }. An NFA is a 5 -tuple: M = (Q, , , s, F) where: § § § Q - a finite set of states - a finite alphabet s – the start state F Q – the set of final states : Q P(Q), the power set of Q. 2004 SDU 10

NFA -definition Let N =(Q, , , q 0, F) be an NFA and w a string over the alphabet . We say N accepts w if we can write w as w = y 1…ym , where each yi is a member of and a sequence of states p 0, …, pm exists with three conditions: 1. p 0=q 0; 2. for every i, 1 i m, pi (pi-1, yi); 3. pm F Language recognized by an NFA N, denoted as L(N), is the set of the strings accepted by N. 2004 SDU 11

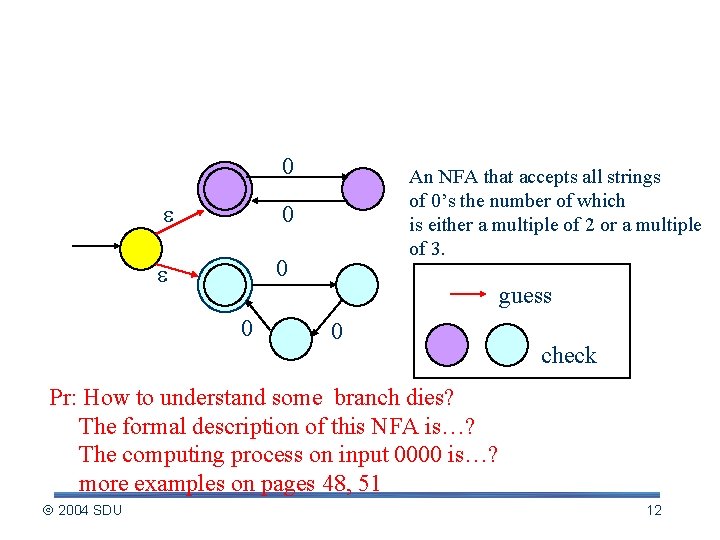
Example of NFA 0 0 0 An NFA that accepts all strings of 0’s the number of which is either a multiple of 2 or a multiple of 3. guess 0 0 check Pr: How to understand some branch dies? The formal description of this NFA is…? The computing process on input 0000 is…? more examples on pages 48, 51 2004 SDU 12

NFA vs. DFA Is NFA more powerful than DFA? § Ans: No. Theorem: § For every NFA M there is an equivalent DFA M' Proof Idea: § NFA is in a set of states at any point during reading a string. § DFA will use a state to keep track of this. Important Assumption: § No transition labeled by epsilon. (Will get rid of this assumption later. ) 2004 SDU 13

Equivalent DFA construction. NFA N = (Q, , , s, F) DFA M = (Q', , , s', F') where: § Q' = p(Q), power set of Q § s' = {s} § F' = {P Q' | P F is nonempty} § ({q 1, …, qm}, a) = (q 1, a) (q 2, a) . . . (qm, a) i. e. find all the states that can be reached on a from all the NFA states in a DFA state. 2004 SDU 14

How to handle epsilon transitions? Define e-closure of state P, E(P) = {q|q can be reached from some p P by traveling along 0 or more arrows}. Let: ({q 1, …, qm}, a) = {q Q| q E( (q 1, a)) E( (q 2, a)) . . . E( (qm, a)) Let: s’=E(s) Proof: at each step of M on an input, it clearly enters a state that corresponds to the subset of states that N could be in at that point. See page 56. See page 57, example 1. 41 2004 SDU 15

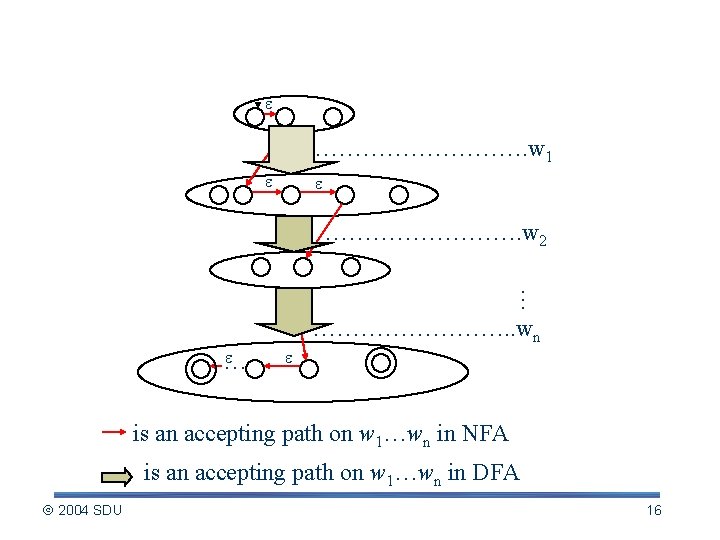
Construct DFA from NFA ……………. w 1 …………. w 2 … … …………. . wn … is an accepting path on w 1…wn in NFA is an accepting path on w 1…wn in DFA 2004 SDU 16

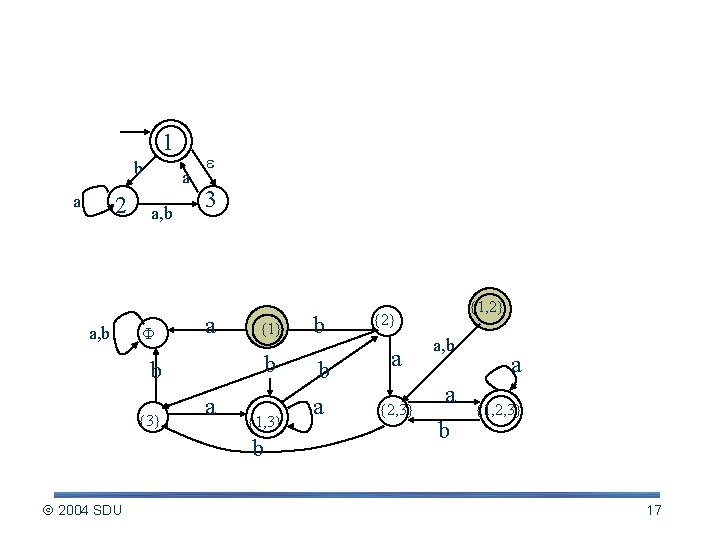
Construct from NFA to DFA (example) 1 b a 2 a, b a a, b 3 a {1} b b {3} a {1, 3} b 2004 SDU b b a {1, 2} {2} a {2, 3} a, b a {1, 2, 3} 17

Regular languages Conclusion: A language is regular iff some NFA recognizes it. 2004 SDU 18

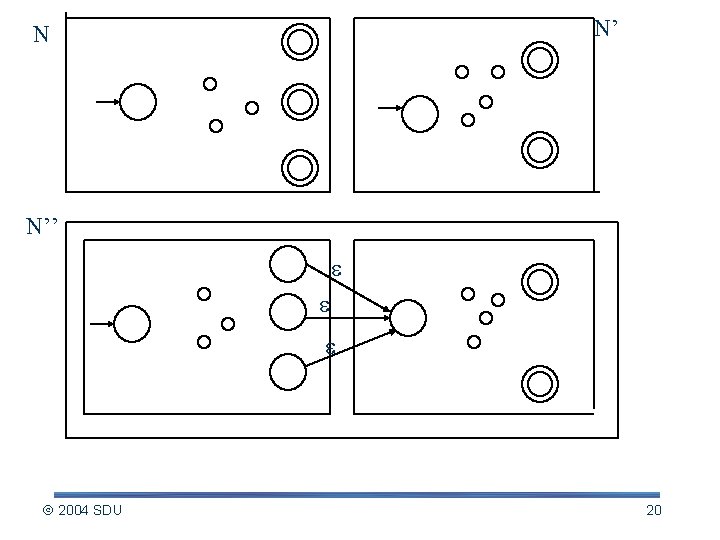
Construction for LºL‘ page 60 Let L=(Q 1, , 1, s 1, F 1); L’=(Q 2, , 2, s 2, F 2) Define: L’’ = (Q, , , s, F), where Q = Q 1 Q 2 s = s 1 F = F 2 2004 SDU 19

N’ N N’’ 2004 SDU 20

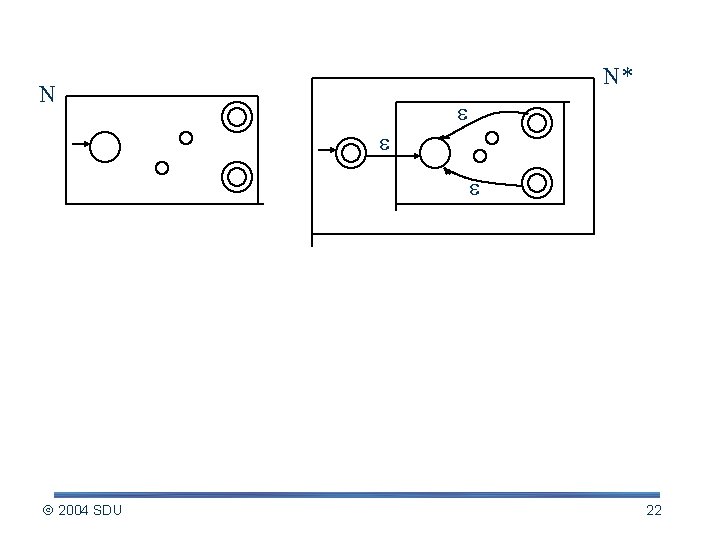
L* Let L=(Q 1, , 1, s 1, F 1) Define: L* = (Q, , , s, F) Q = {s} Q 1 F = {s} F 1 2004 SDU 21

N* N 2004 SDU 22