Closure Properties DFA Languages which have DFA that

Closure Properties DFA L L* Y Y Y NFA Reg Exp We will give

MDFA = DFA (MDFA 1, MDFA 2) Closure Properties L 1 = {a {0,

MDFA = DFA (MDFA 1, MDFA 2) Closure Properties The two algorithms are simply

MDFA = DFA (MDFA 1, MDFA 2) Closure Properties The new DFA runs the

MDFA = DFA (MDFA 1, MDFA 2) Closure Properties a = 01010 In parallel,

MDFA = DFA (MDFA 1, MDFA 2) Closure Properties L 1 L 2 =

Closure Properties L 1∙L 2 = { αβ | αϵL 1 and βϵL 2

MNFA* = NFA*(MNFA 1, MNFA 2) Closure Properties L* = { α 1α 2α

MNFA = NFA (MNFA 1, MNFA 2) Closure Properties Union: L 1 L 2

MNFA = NFA (MNFA 1, MNFA 2) Closure Properties Intersection: L 1 L 2

MNFA = NFA (MNFA 1, MNFA 2) Closure Properties Complement: L = { α

a = abbabaaba Input NFA to DFA • We will have clones work in

Extended Regular Expression to NFA (a*b a*bb) a* b* ERegto. NFA(R) Precondition: R is

Extended Regular Expression to NFA Recursion: Routine calls itself. (Asks friends for help). 0

NFA to Regular Expression (a*b a*bb) a*b* Maintaining Loop Invariant <loop-invariantt> ¬<exit Cond> code.

The Bumping Lemma We say that language L distinguishes between string α and β

The Bumping Lemma Theorem: No DFA solves L = 0 n 1 n. Suppose

The Bumping Lemma Theorem: No DFA solves L = 0 n 1 n. I

Slides: 32

Download presentation

Closure Properties DFA Languages which have DFA that solve them DFA MDFA 1 such that L(MDFA 1) = L 1 DFA MDFA 2 such that L(MDFA 2) = L 2 L 1 L 2 We will give an algorithm MDFA = DFA (MDFA 1, MDFA 2) such that L(MDFA ) = L(MDFA 1) L(MDFA 2) DFA MDFA such that L(MDFA ) = L 1 L 2 1

Closure Properties DFA L L* Y Y Y NFA Reg Exp We will give an algorithm MDFA = DFA (MDFA 1, MDFA 2) such that L(MDFA ) = L(MDFA 1) L(MDFA 2) Ext Reg Exp Y ? ? Y Y Y Y 2

MDFA = DFA (MDFA 1, MDFA 2) Closure Properties L 1 = {a {0, 1}* | a has length at most three } L 2 = {a {0, 1}* | the number of 1's is odd } L 1 L 2 = {a {0, 1}* | a has length at most three and the number of 1's is odd } 3

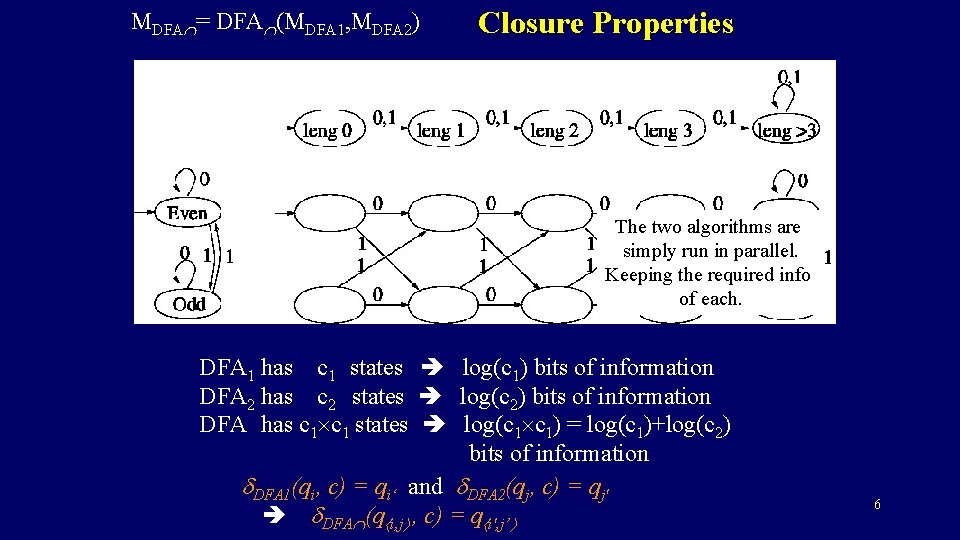
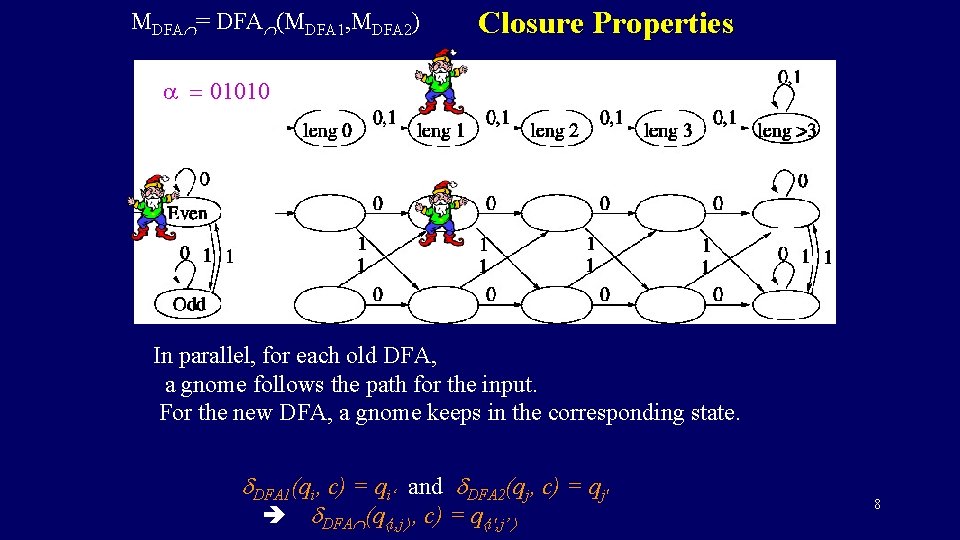
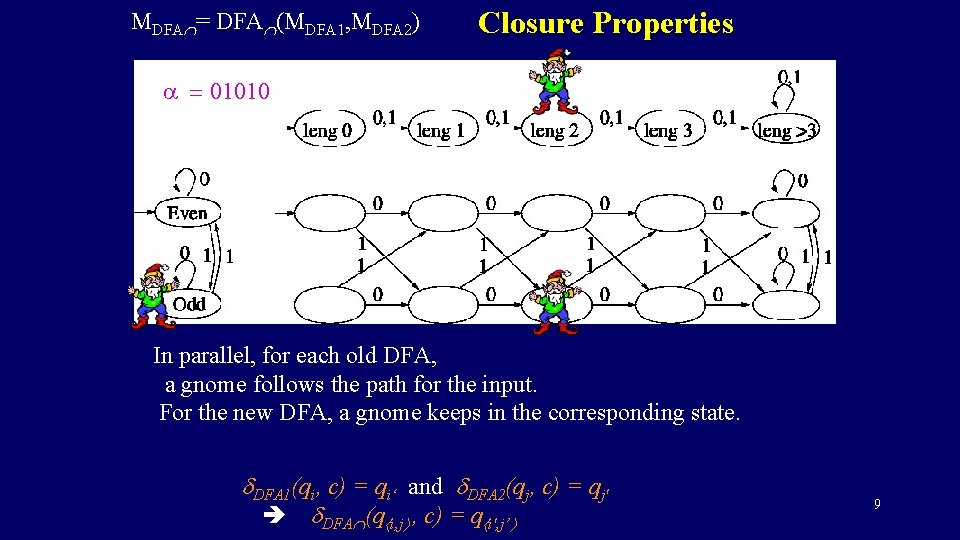
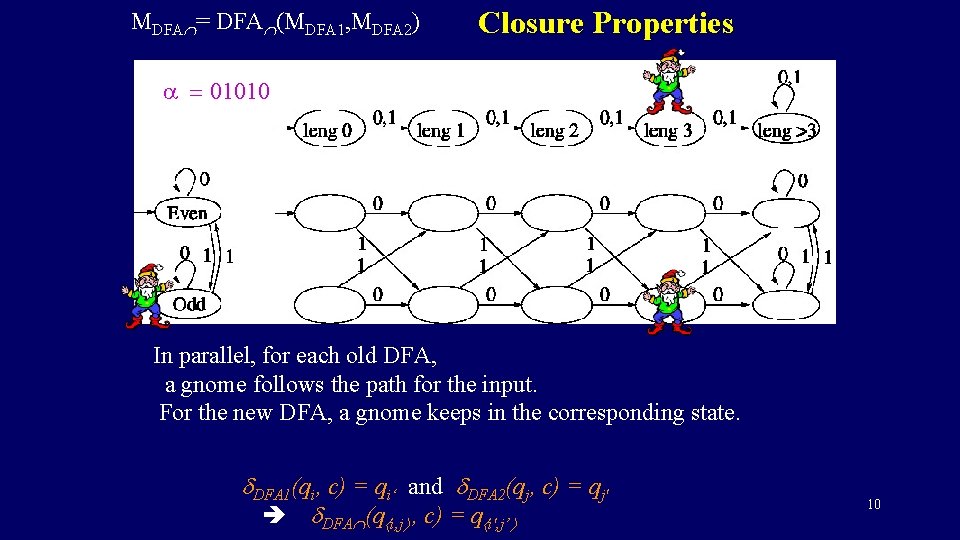
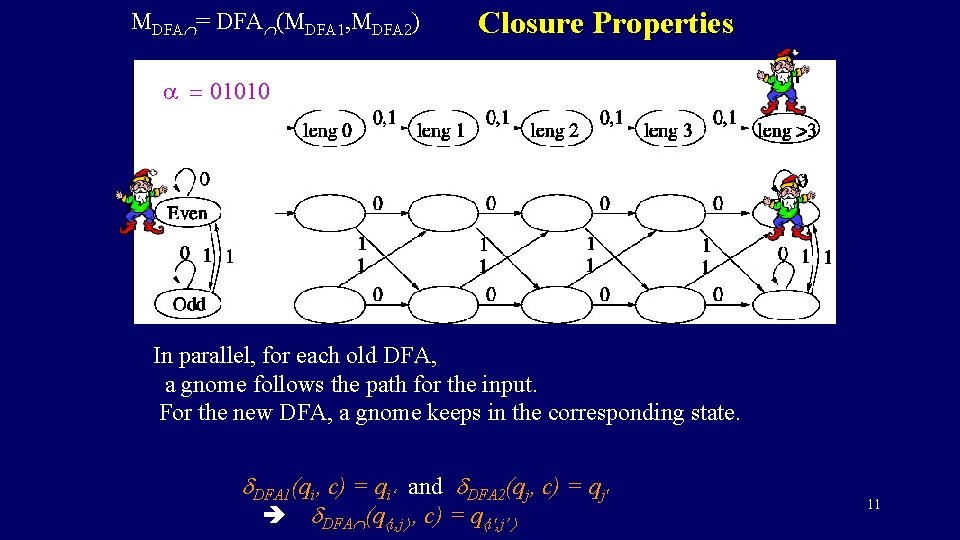
MDFA = DFA (MDFA 1, MDFA 2) Closure Properties The two algorithms are simply run in parallel. Keeping the required info of each. 4

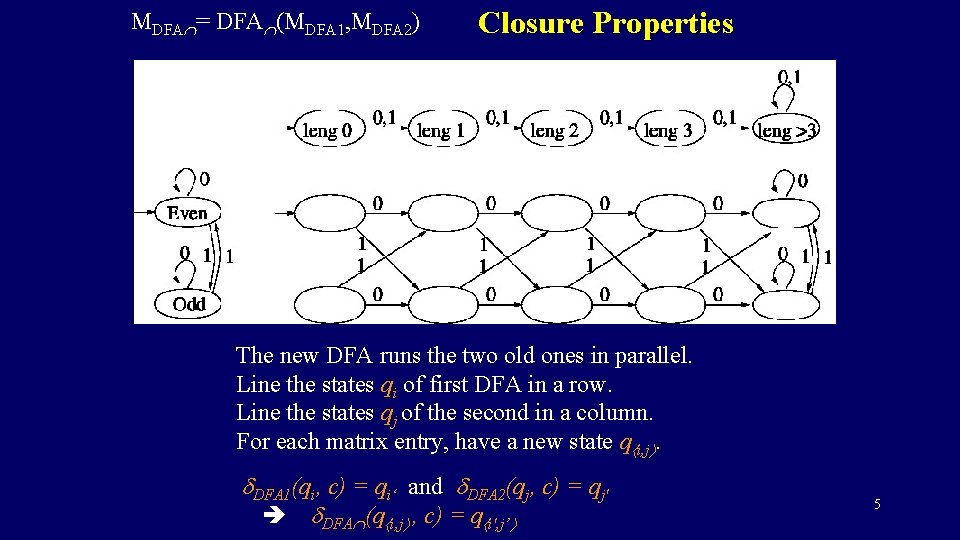
MDFA = DFA (MDFA 1, MDFA 2) Closure Properties The new DFA runs the two old ones in parallel. Line the states qi of first DFA in a row. Line the states qj of the second in a column. For each matrix entry, have a new state q i, j. DFA 1(qi, c) = qi‘ and DFA 2(qj, c) = qj' DFA (q i, j , c) = q i', j’ 5

MDFA = DFA (MDFA 1, MDFA 2) Closure Properties The two algorithms are simply run in parallel. Keeping the required info of each. DFA 1 has c 1 states log(c 1) bits of information DFA 2 has c 2 states log(c 2) bits of information DFA has c 1 states log(c 1 c 1) = log(c 1)+log(c 2) bits of information DFA 1(qi, c) = qi‘ and DFA 2(qj, c) = qj' DFA (q i, j , c) = q i', j’ 6

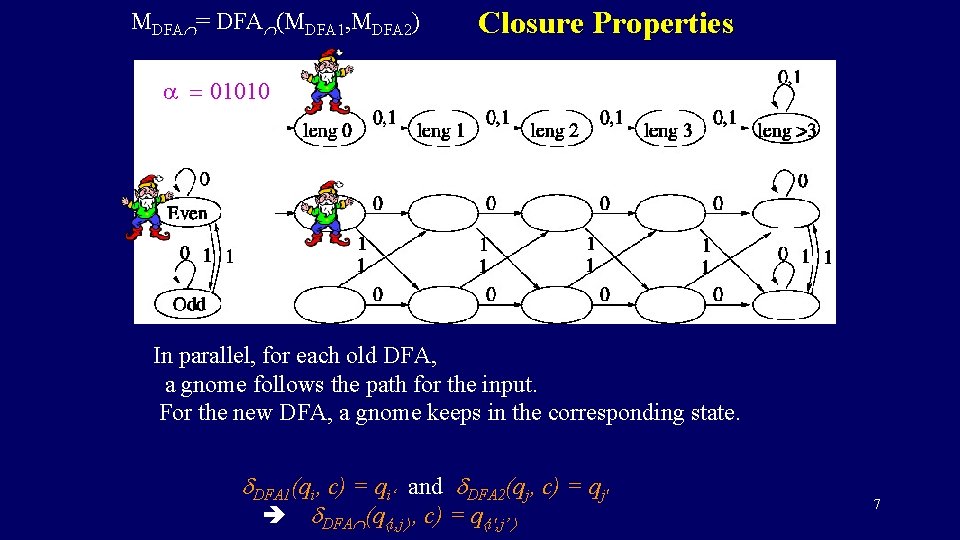
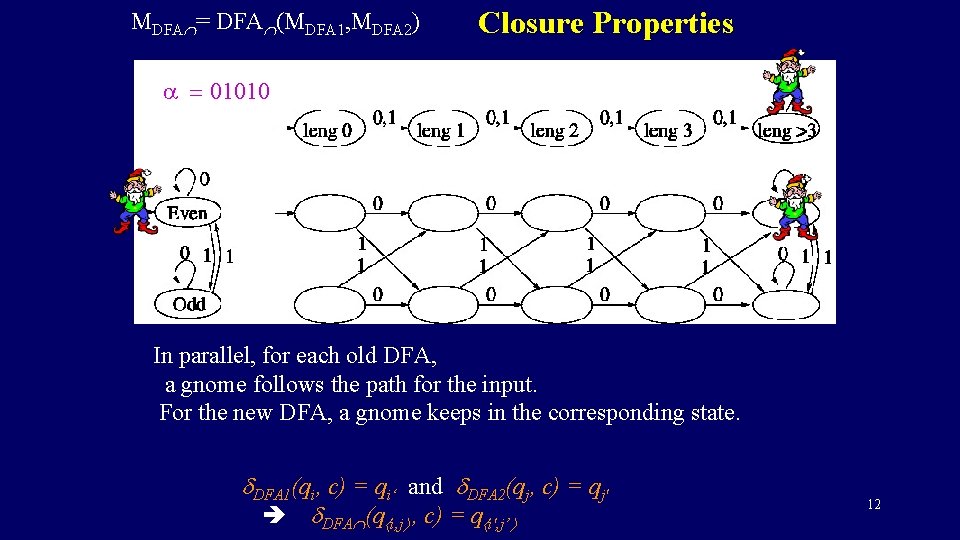
MDFA = DFA (MDFA 1, MDFA 2) Closure Properties a = 01010 In parallel, for each old DFA, a gnome follows the path for the input. For the new DFA, a gnome keeps in the corresponding state. DFA 1(qi, c) = qi‘ and DFA 2(qj, c) = qj' DFA (q i, j , c) = q i', j’ 7

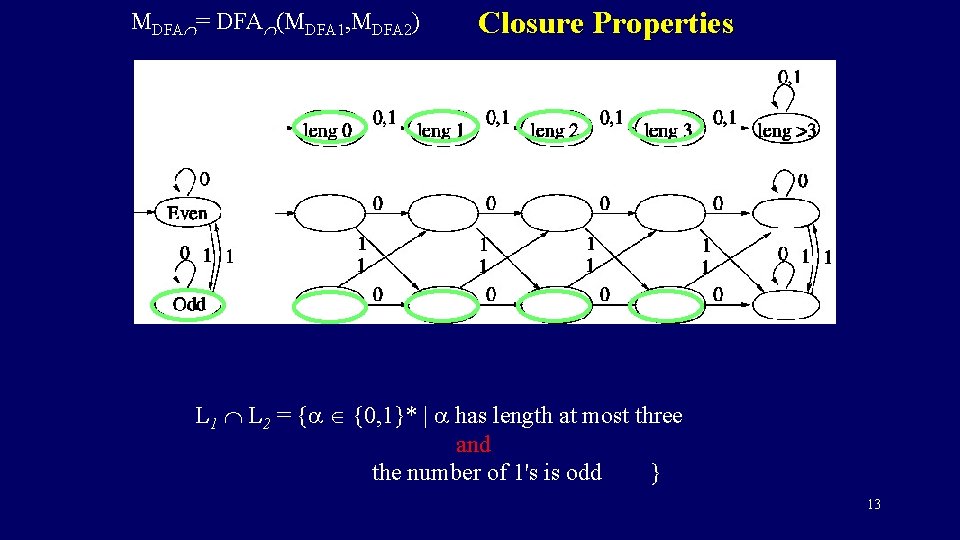
MDFA = DFA (MDFA 1, MDFA 2) Closure Properties L 1 L 2 = {a {0, 1}* | a has length at most three and the number of 1's is odd } 13

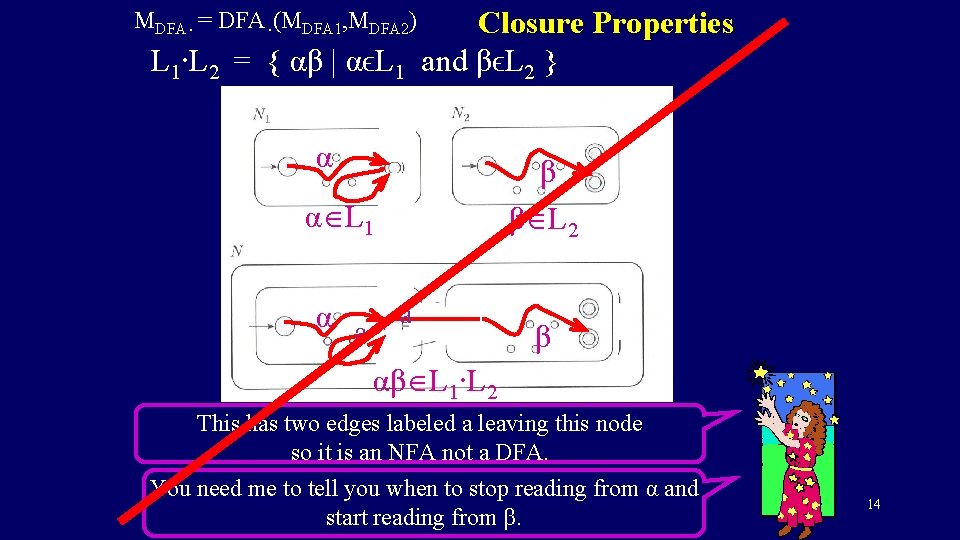
Closure Properties L 1∙L 2 = { αβ | αϵL 1 and βϵL 2 } MDFA∙ = DFA∙(MDFA 1, MDFA 2) α β β L 2 α L 1 α a a β αβ L 1∙L 2 This has two edges labeled a leaving this node so it is an NFA not a DFA. You need me to tell you when to stop reading from α and start reading from β. 14

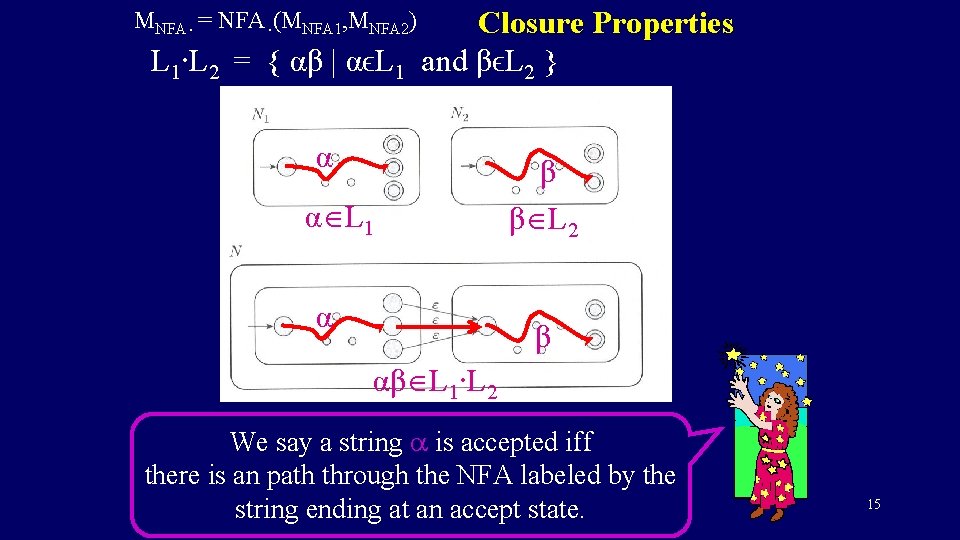
Closure Properties L 1∙L 2 = { αβ | αϵL 1 and βϵL 2 } MNFA∙ = NFA∙(MNFA 1, MNFA 2) α α L 1 α β β L 2 β αβ L 1∙L 2 We say a string a is accepted iff there is an path through the NFA labeled by the string ending at an accept state. 15

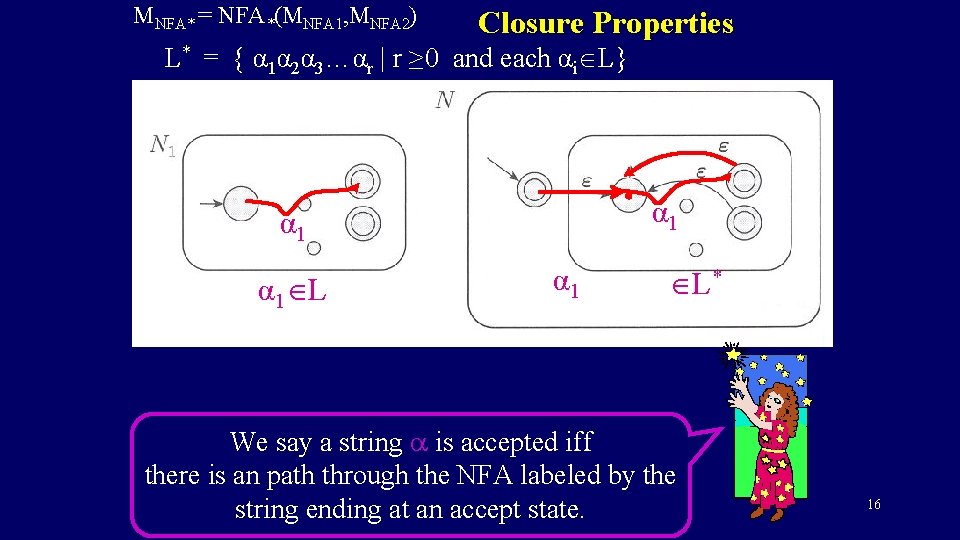
MNFA* = NFA*(MNFA 1, MNFA 2) Closure Properties L* = { α 1α 2α 3…αr | r ≥ 0 and each αi L} α 1 α 1 L α 1 L* We say a string a is accepted iff there is an path through the NFA labeled by the string ending at an accept state. 16

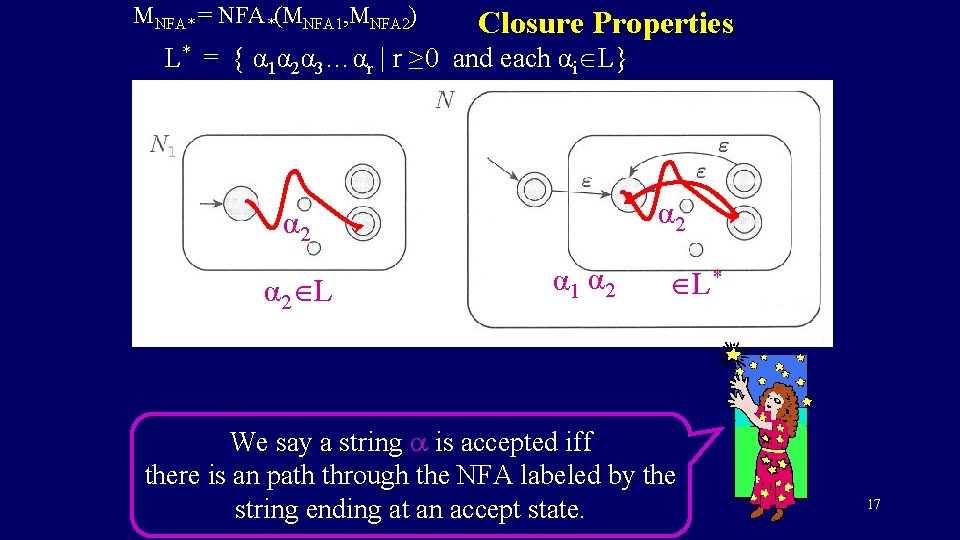
MNFA* = NFA*(MNFA 1, MNFA 2) Closure Properties L* = { α 1α 2α 3…αr | r ≥ 0 and each αi L} α 2 α 2 L α 1 α 2 L* We say a string a is accepted iff there is an path through the NFA labeled by the string ending at an accept state. 17

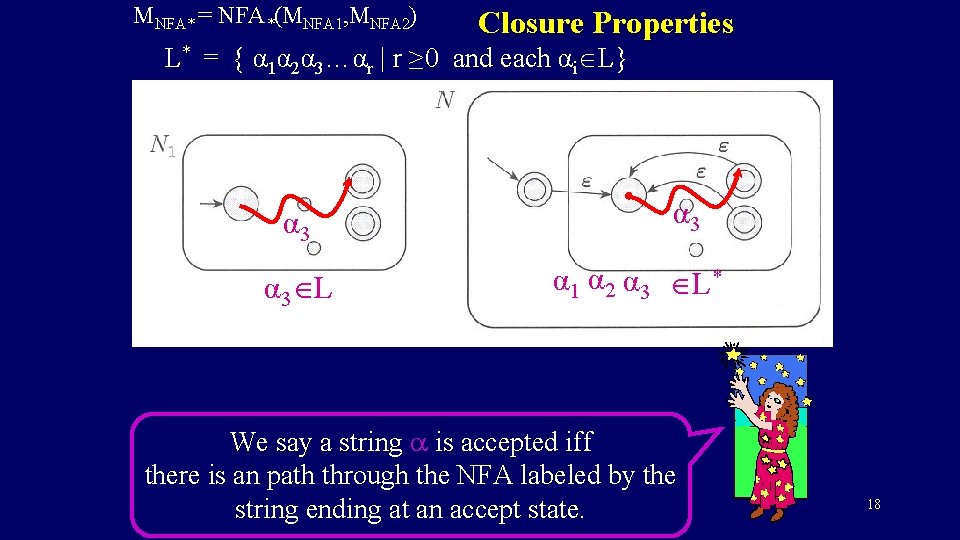
MNFA* = NFA*(MNFA 1, MNFA 2) Closure Properties L* = { α 1α 2α 3…αr | r ≥ 0 and each αi L} α 3 L α 3 α 1 α 2 α 3 L* We say a string a is accepted iff there is an path through the NFA labeled by the string ending at an accept state. 18

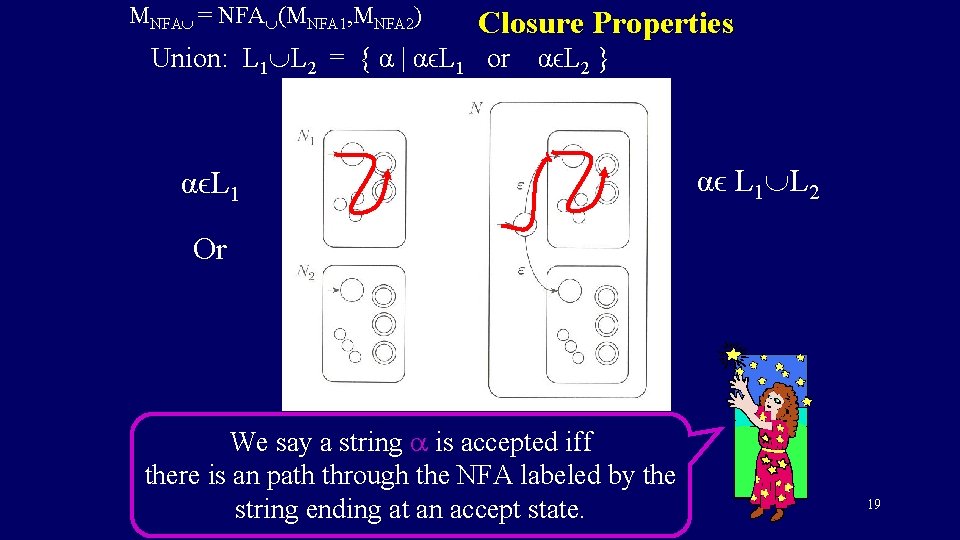
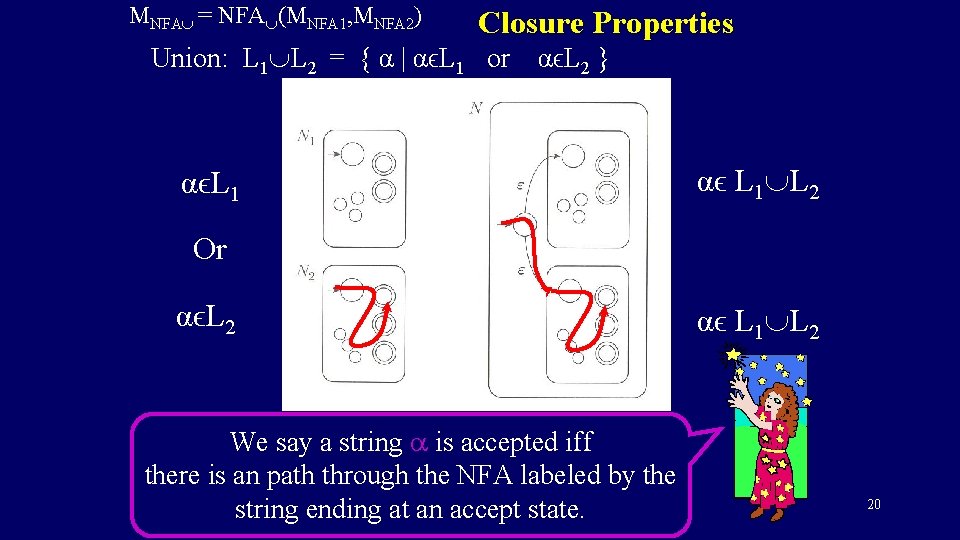
MNFA = NFA (MNFA 1, MNFA 2) Closure Properties Union: L 1 L 2 = { α | αϵL 1 or αϵL 2 } αϵL 1 αϵ L 1 L 2 Or We say a string a is accepted iff there is an path through the NFA labeled by the string ending at an accept state. 19

MNFA = NFA (MNFA 1, MNFA 2) Closure Properties Union: L 1 L 2 = { α | αϵL 1 or αϵL 2 } αϵL 1 αϵ L 1 L 2 Or αϵL 2 We say a string a is accepted iff there is an path through the NFA labeled by the string ending at an accept state. αϵ L 1 L 2 20

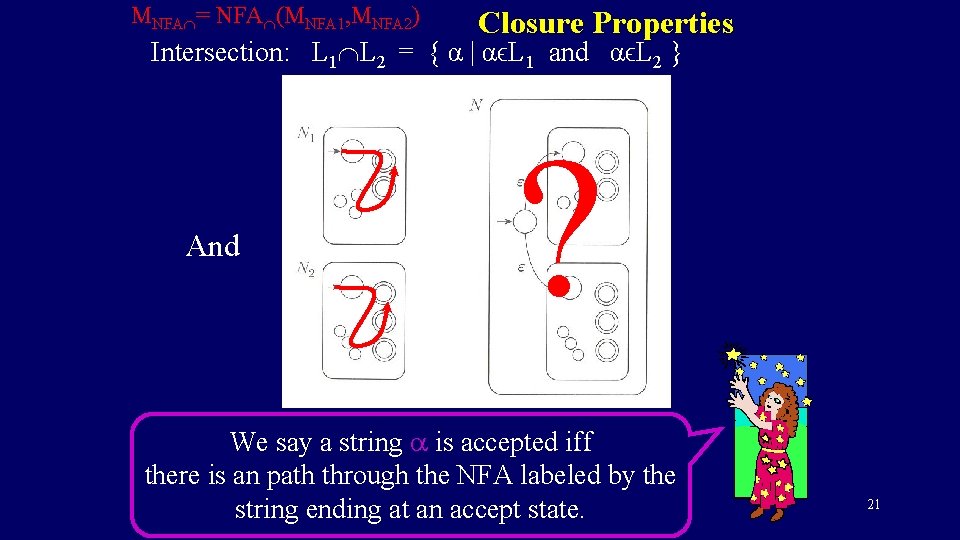
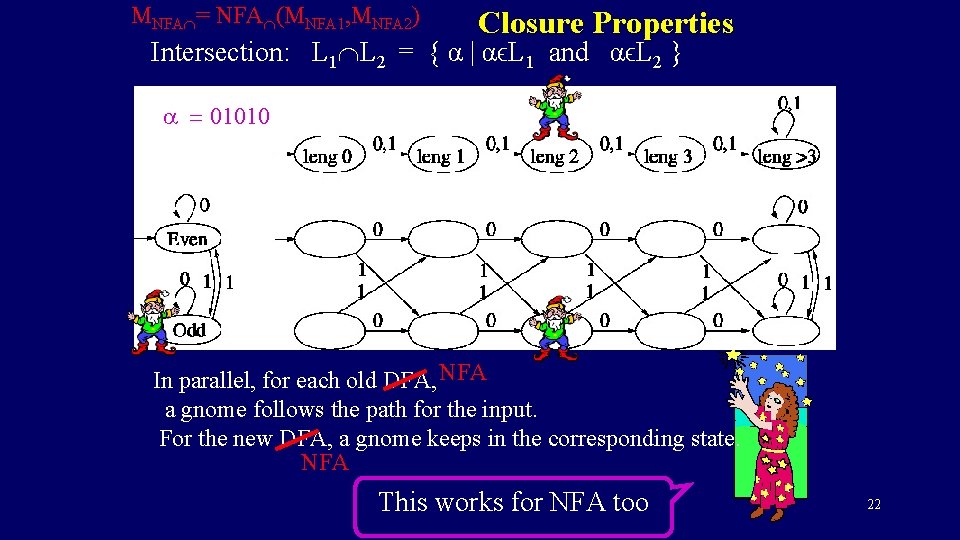
MNFA = NFA (MNFA 1, MNFA 2) Closure Properties Intersection: L 1 L 2 = { α | αϵL 1 and αϵL 2 } And ? We say a string a is accepted iff there is an path through the NFA labeled by the string ending at an accept state. 21

MNFA = NFA (MNFA 1, MNFA 2) Closure Properties Intersection: L 1 L 2 = { α | αϵL 1 and αϵL 2 } a = 01010 In parallel, for each old DFA, NFA a gnome follows the path for the input. For the new DFA, a gnome keeps in the corresponding state. NFA This works for NFA too 22

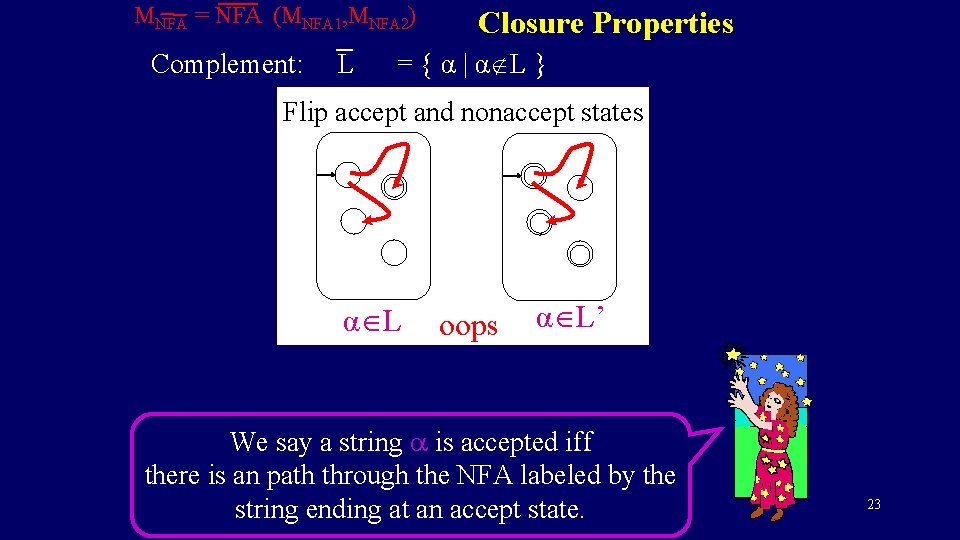
MNFA = NFA (MNFA 1, MNFA 2) Closure Properties Complement: L = { α | α L } Flip accept and nonaccept states α L oops α L’ We say a string a is accepted iff there is an path through the NFA labeled by the string ending at an accept state. 23

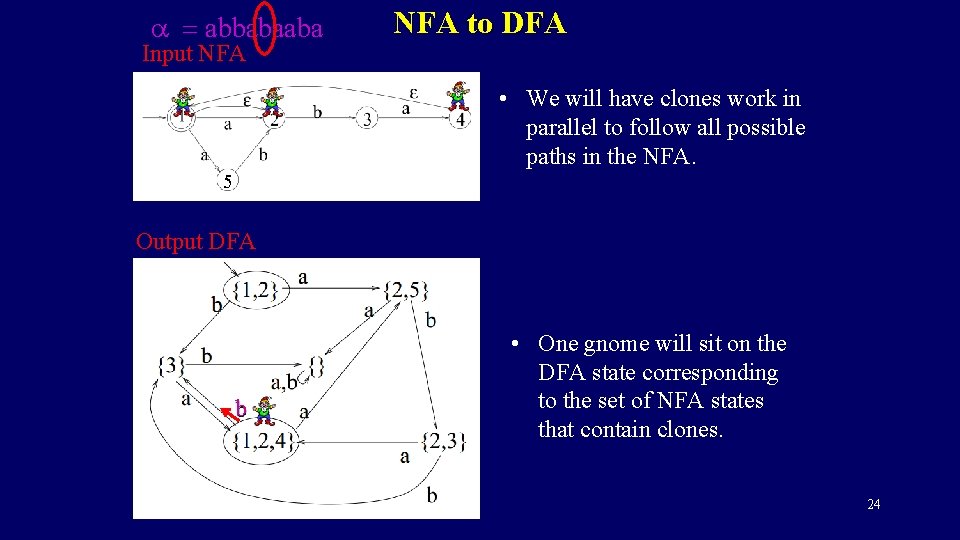
a = abbabaaba Input NFA to DFA • We will have clones work in parallel to follow all possible paths in the NFA. 5 Output DFA b • One gnome will sit on the DFA state corresponding to the set of NFA states that contain clones. 24

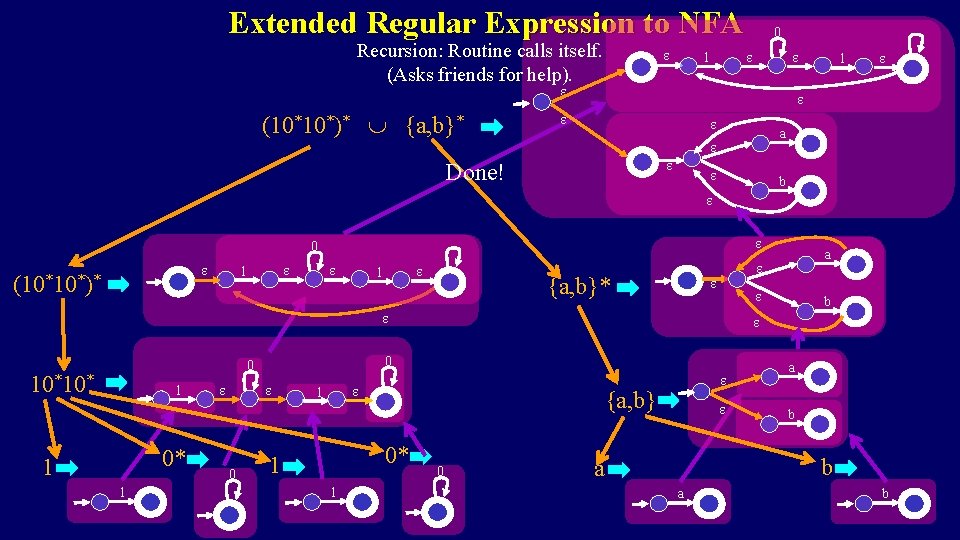
Extended Regular Expression to NFA (a*b a*bb) a* b* ERegto. NFA(R) Precondition: R is an extended regular repression Postcondition: M is an NFA accepting the same language if( R = R 1 R 2 ) % Eg R = (10*10*)* {a, b}* % Get help from recursive friends M 1 = ERegto. NFA(R 1) M 2 = ERegto. NFA(R 2) M = NFA (M 1, M 2) return( M ) Don’t micro manage me. Just trust me to do my job on any smaller instance of the same problem. DFA NFA Reg Exp Ext Reg Exp L L* Y Y Y ? ? Y Y Y ? Y

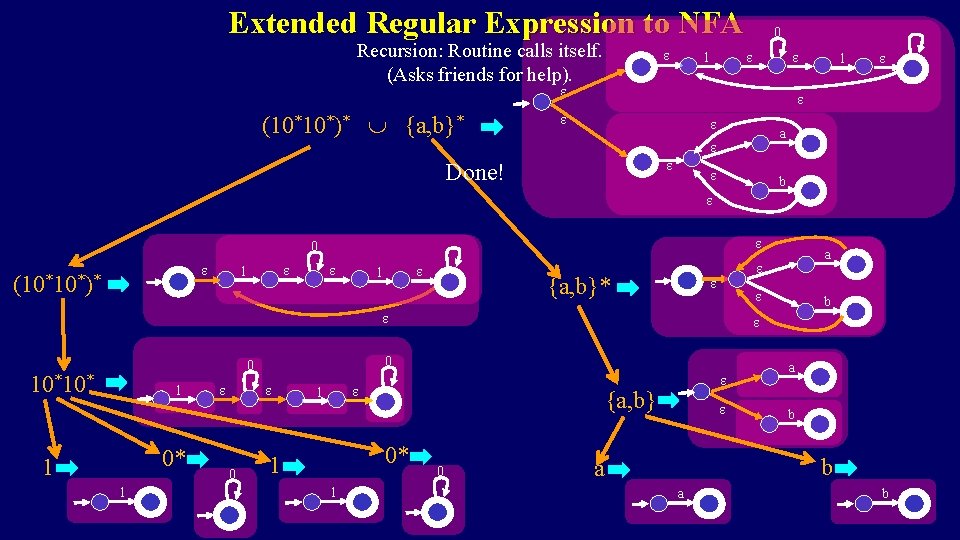
Extended Regular Expression to NFA Recursion: Routine calls itself. (Asks friends for help). 0 1 (10*10*)* {a, b}* 1 a Done! b 0 (10*10*)* 1 1 {a, b}* 10*10* 1 1 0 1 1 {a, b} 0* 1 b 0 0 a b b a a b

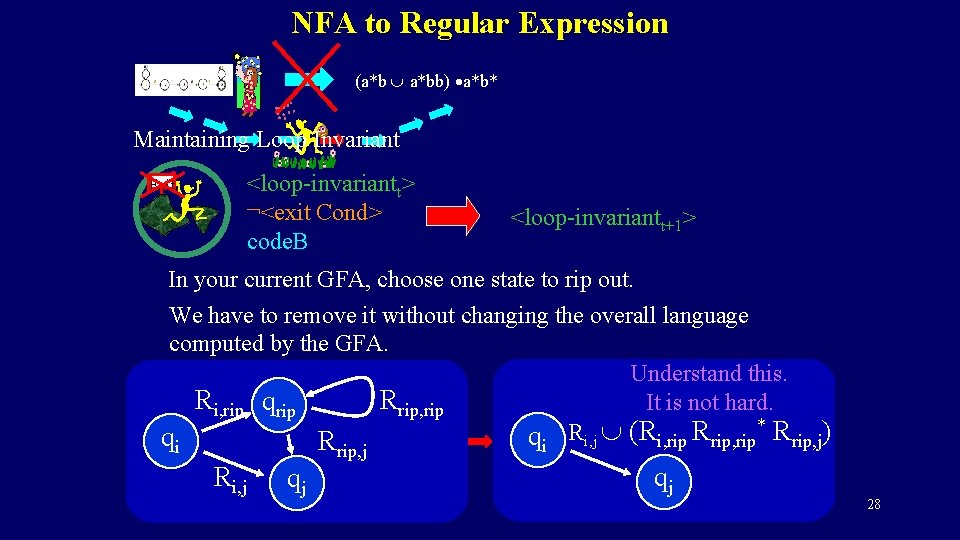
NFA to Regular Expression (a*b a*bb) a*b* Maintaining Loop Invariant <loop-invariantt> ¬<exit Cond> code. B Exit <loop-invariantt+1> In your current GFA, choose one state to rip out. We have to remove it without changing the overall language computed by the GFA. Understand this. Rrip, rip Ri, rip qrip It is not hard. * R R (R R q i, j q i, rip rip, j) R i rip, j Ri, j qj i qj 28

The Bumping Lemma We say that language L distinguishes between string α and β iff there We say that language L distinguishes between string exists a string ζ such that L gives different answers to αζ and βζ. We say a set S of strings is distinguished if every pair in it are. Bumping Lemma: " DFA M with |M| < |S|, $ input I, M(I)≠L(I) I produce a DFA M with |M| < |S|. L(αζ) ≠ L(βζ) M(αζ) = M(βζ) Either M(αζ) ≠ L(αζ) or M(βζ) ≠ L(βζ) start α β … α β ζ Accept

The Bumping Lemma We say that language L distinguishes between string α and β iff there We say that language L distinguishes between string exists a string ζ such that L gives different answers to αζ and βζ. We say a set S of strings is distinguished if every pair in it are. Bumping Lemma: No DFA with fewer than |S| states solves L. S = {Jeff , Suprakash, Patrick } Ie. Linvite needs at least 3 states. Jeff start Suprakash Eric Edmonds Ruppart Suprakash Edmonds Datta Eric Ruppart Patrick Datta Dymond Accept

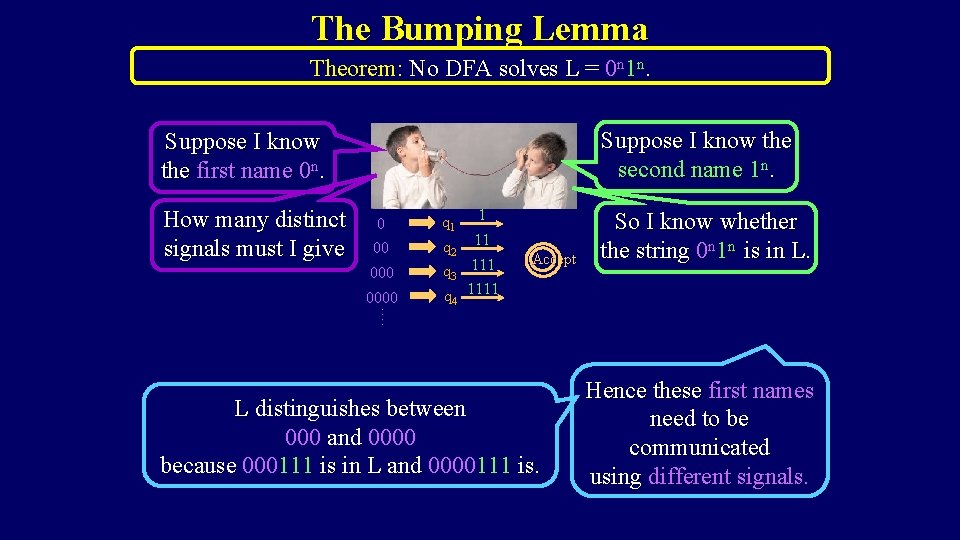
The Bumping Lemma Theorem: No DFA solves L = 0 n 1 n. Suppose I know the second name 1 n. Suppose I know the first name 0 n. How many distinct signals must I give 0 q 1 00 q 2 0000 1 11 q 3 111 q 1111 Accept So I know whether the string 0 n 1 n is in L. …. 4 L distinguishes between 000 and 0000 because 000111 is in L and 0000111 is. Hence these first names need to be communicated using different signals.

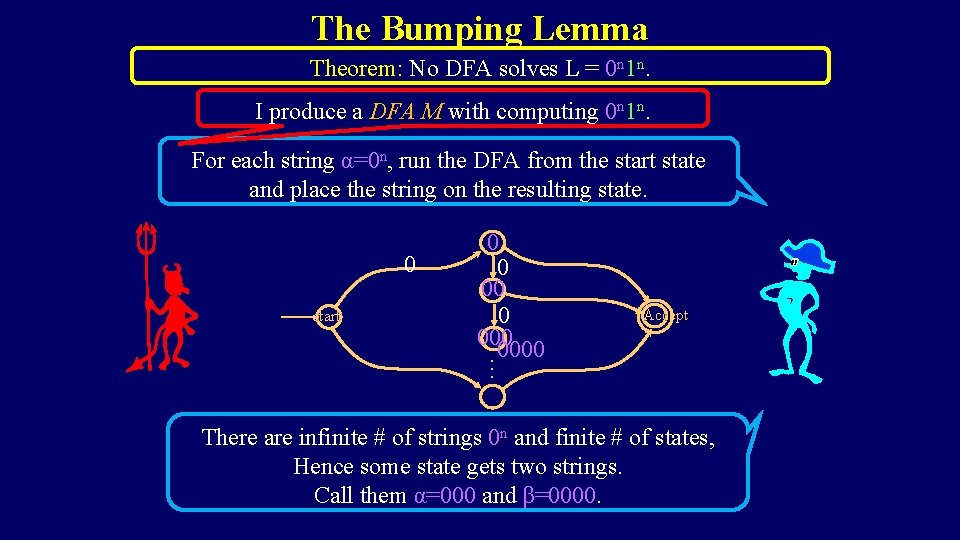
The Bumping Lemma Theorem: No DFA solves L = 0 n 1 n. I produce a DFA M with computing 0 n 1 n. For each string α=0 n, run the DFA from the start state and place the string on the resulting state. 0 start Accept … 0 0 000 0000 There are infinite # of strings 0 n and finite # of states, Hence some state gets two strings. Call them α=000 and β=0000.