Electronic stopping power of ions in insulator as

Electronic stopping power of ions in insulator as calculated by TD-DFT Emilio Artacho Department of Earth Sciences University of Cambridge

Miguel Pruneda Physics, UC Berkeley Collaborators Donostia International Physics Centre Daniel Sanchez-Portal (implementation) Andres Arnau Inaki Juaristi Pedro Echenique & Discussions with Txema Pitarke Peter Bauer (Linz, Austria) Thanks to the Miller Institute at UCB & Thanks to

Immobilisation of nuclear waste by dilution in ceramics SYNthetic ROCks with appropriate “minerals” to host high level nuclear waste Research in durability: We need them to last for ~ 1 My Resistance to radiation damage Zircons have contained uranium for billions of years

Durability: Radiation damage α-particle α-decay process ~ 5 Me. V It causes: • Amorphisation (metamict) Recoil ~ 100 ke. V • Swelling • Cracks • Leaching Zircon: model study: old natural samples

Recoil damage: amorphisation zircon K. Trachenko & M. T. Dove, with empirical potentials

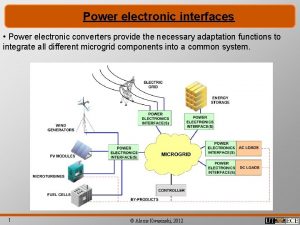
Electrons heat up: effect on the material? Effect on the simulations? The ion moving in the solid transmits energy to electrons. How much? How? Where? What consequences does it have? Coupled dynamics of both electrons & nuclei (realistic simulation demands ~ 2 M atoms)

Multiscale: Different timescales • this study (electronic excitation) • electron-phonon coupling + • heat conductivities for the electron and phonon subsystems ÞContinuum description of excess energy Eel ( r, t) First: how much energy is it pumped to the electrons per unit time

Energy transfered to electrons: Measured by electronic stopping power d. E/dx High v: Bethe (e. V/Ang) Low (and intermediate) v: Fine underst. Metals, P. T. v (atomic units) 100 ke. V Recoiling Th nucleus: v = 0. 1 a. u.

Electronic versus nuclear stopping Metals: S~v for v -> 0 Nuclear stopping dominates at low velocities

Stopping in noble gases Scattering cross section of H+ on He and Ne Nuclear stoppin g Experiments: JT Park & EJ Zimmerman, Phys. Rev. 131, 1611 (1963) A Schiefermuller et al. Phys. Rev. A 48, 4467 (1993) Calculations: R Cabrera-Trujillo et al. , PRL 84, 5300 (2000)

Electronic stopping in insulators: different? C Auth et a. PRL 81, 4831 (1998) Protons onto Li. F: (5 ke. V ~ v = 1 a. u. ) Grazing angle (on the surface) Threshold

Electronic stopping power in Li. F Across thin films H V = 0. 4 a. u. d. E/dx = 0. 12 a. u. = 6. 2 e. V/Ang (But 1. 6 error) Juaristi et al, PRL 84, 2124 (2000) No threshold = 3. 9 e. V/Ang

Protons and antiprotons into Li. F thin films “Antiproton Stopping at Low Energies: Confirmation of Velocity-Proportional Stopping Power” SP Møller et al. PRL 88, 193201 (2002) & PRL 93, 042512 (2004) No threshold

Protons into Li. F thin films again M. Draxler et al, PRL 95, 113201 (2005) Scale: v = 0. 1 a. u. => Stopping ~ 1 e. V/Ang Threshold

Threshold: what to expect? TD Pertub. Th. (weak projectile potential) e-h excitations such that / k = v Strict threshold: 1/2 (me +mh)vc 2 = Egap Exc: V(q= k)

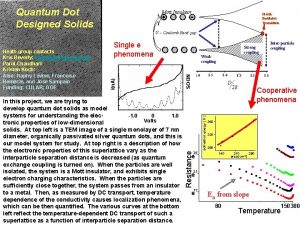
TD-DFT: Our approach • Supercell of insulator’s bulk • Periodic boundary conditions • Density functional theory • Add external charge (potential) • Move it and follow electron wave-functions with Time-Dependent DFT

The SIESTA method Linear-scaling DFT based on NAOs (Numerical Atomic Orbitals) P. Ordejon, E. Artacho & J. M. Soler , Phys. Rev. B 53, R 10441 (1996) • Born-Oppenheimer (relaxations, mol. dynamics) • DFT (LDA, GGA) • Pseudopotentials (norm conserving, factorised) • Numerical atomic orbitals as basis (finite range) • Numerical evaluation of matrix elements (3 D grid) Implemented in the SIESTA program J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon & D. Sanchez-Portal, J. Phys. : Condens. Matter 14, 2745 (2002)

Time dependent DFT Usual (stationary) DFT: Time-dependent DFT: Neither forces on atoms (no MD), nor moving basis

Real time evolution of the density • SIESTA (LCAO) • Evolution of the TD-KS equations: Crank-Nicholson

Energy as a function of distance: Li. F Quite stationary! Short transient, no obvious oscillation

Rate of energy transfer: electronic stopping powe Protons and antiprotons through Li. F Threshold ~ 0. 2 a. u. (exp ~ 0. 1) Ratio SPp/SPa ~ 2. 4 (exp ~ 2. 1)

Rate of energy transfer: electronic stopping powe Protons and antiprotons through Li. F Threshold ~ 0. 2 a. u. (exp ~ 0. 1) Ratio SPp/SPa ~ 2. 4 (exp ~ 2. 1) Absolute value: improve basis; sp basis along trajectory (for p)

Rate of energy transfer: electronic stopping powe Protons and antiprotons through Li. F Threshold ~ 0. 2 a. u. (exp ~ 0. 1) Ratio SPp/SPa ~ 2. 4 (exp ~ 2. 1) Absolute value ~ 20 -50% too small as compared to experiment But: Th is channelling, exp is average

Stopping power dependence on charge For small positive charges, the linear regime is recovered. d. E/dx ~ q 2 v (small perturbation)

Evolution of the charge on nearby Li atoms v=1 au v= 0 Nearest neighb. 2 nd nearest neighb. Position of projectile along trajectory (x=0 closest to nearest Li) Screening of charge enhanced at finite v Extremely short-ranged mechanism

Locality in the electronic stopping power Protons in Li. F Compare bulk with small cluster Li 6 F 5+

Further Channeling vs average trajectories: Electronic stopping power in channels ~ average/2 JJ Dorado & F Flores, PRA 47, 3062 (1993) Combine nuclear & electron stopping Requires simultaneous dynamics. Hard technically and computationally (time scales) Charge states (momentum) Interesting. Right question to pose.

Summary • Using TD-DFT for obtaining the energy transfer from moving ions to electrons in insulators. • New approach, complementary • Offers new kinds of information • Lots to do! Important: Recoiling velocity around threshold

Funding

Flat-band limit: Simple model

Evolution of the charge

Atomic Energies “Hamiltonian Population” Mulliken Atomic/Overlap Population Hamiltonian Atomic/Overlap Population: a way of defining “local energy” in our problem LCAO simplest version of energy density – R. M. Martin PRB-(‘ 92)

Evolution of the local energy

Flat-band limit: Simple model Gaussian perturbation as V 0

Dependence on basis set & other approx Dependence on technicalities (supercell size, numerical integrations, pseudos) But also on more fundamental aspects (Charge state, DFT kernel: instantaneous LDA)