Determinan Matriks Sub Pokok Bahasan Determinan Matriks Determinan

Determinan Matriks Sub Pokok Bahasan Determinan Matriks Determinan dengan Ekspansi Kofaktor Sifat Determinan Aljabar Linear 1

Aplikasi penggunaan determinan • Beberapa Aplikasi Determinan – – Solusi SPL Optimasi Model Ekonomi dan lain-lain

Definisi Determinan Matriks Hasil kali elementer A hasilkali n buah unsur A tanpa ada pengambilan unsur dari baris/kolom yang sama. Contoh : Ada 6 (3!) hasil kali elementer dari matriks A, yaitu: a 11 a 22 a 33, a 11 a 23 a 32 , a 12 a 21 a 33 , a 12 a 23 a 31 , a 13 a 21 a 32 , a 13 a 22 a 31 Aljabar Linear 3

Hasil kali elementer bertanda a 11 a 22 a 33 Perhatikan… – a 11 a 23 a 32 Tanda (+/-) muncul sesuai hasil – a 12 a 21 a 33 klasifikasi permutasi indeks kolom, a 12 a 23 a 31 yaitu : jika genap + (positif) jika ganjil - (negatif) a 13 a 21 a 32 – a 13 a 22 a 31 Jadi, Misalkan Anxn maka determinan dari matriks A didefinisikan sebagai jumlah dari semua hasil kali elementer bertanda matriks tersebut. Notasi : Det(A) atau |A| Aljabar Linear 4

Contoh : Tentukan Determinan matriks Jawab : Menurut definisi : Det(A 3 x 3) = a 11 a 22 a 33 – a 11 a 23 a 32 – a 12 a 21 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 – a 13 a 22 a 31 atau Aljabar Linear 5
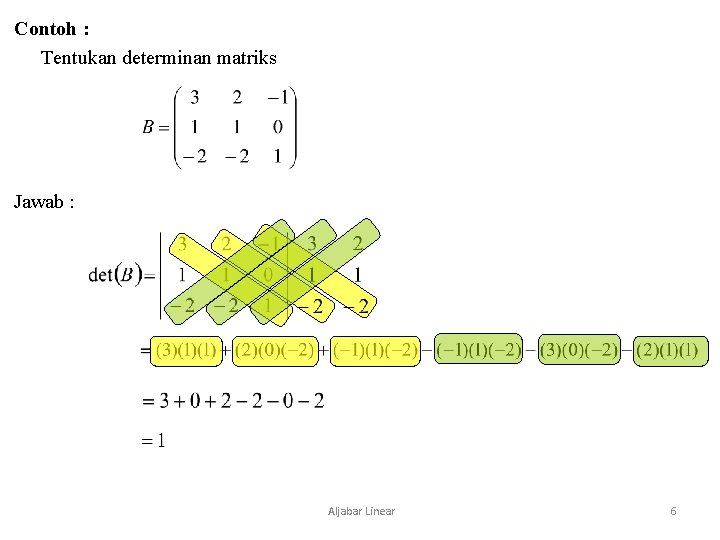
Contoh : Tentukan determinan matriks Jawab : Aljabar Linear 6

Determinan Matrik 2 x 2 Syarat suatu matrik mempunyai determinan: matrik bujursangkar Lambang determinan matrik A adalah det(A) atau A Dengan menggunakan determinan matrik 2 x 2 ini, akan didefinisikan determinan matrik yang berordo yang lebih besar Aljabar Linear 7

Determinan Matrik 3 x 3 det(A)= Dari kenyataan di atas dapat dirumuskan berikut: Aljabar Linier 8

Determinan dengan ekspansi kofaktor Misalkan Beberapa definisi yang perlu diketahui : • Mij disebut Minor- ij yaitu determinan matriks A dengan menghilangkan baris ke_i dan kolom ke-j matriks A. Contoh : 09/03/2021 12: 55 MA-1223 Aljabar Linear 9

• Cij Matrik dinamakan kofaktor - ij yaitu (-1)i+j Mij Contoh : maka = (– 1)3. 2 =– 2 Aljabar Linear 10

Secara umum, cara menghitung determinan dengan ekspansi kofaktor : • Menghitung det (A) dengan ekspansi kofaktor sepanjang baris ke-i det (A) = ai 1 Ci 1 + ai 2 Ci 2 +. . . + ain Cin • Menghitung det (A) dengan ekspansi kofaktor sepanjang kolom ke-j det (A) = aij C 1 j + a 2 j C 2 j +. . . + anj Cjn Contoh 6 : Hitunglah Det(A) dengan ekspansi kofaktor : Aljabar Linear 11

Jawab : Misalkan, kita akan menghitung det (A) dengan ekspansi kofaktor sepanjang baris ke-3 = a 31 C 31 + a 32 C 32 + a 33 C 33 =0– 2+6 =4 Aljabar Linear 12

Menghitung det (A) dengan ekspansi kopaktor sepanjang kolom ke 3 = a 13 C 13 + a 23 C 23 + a 33 C 33 =0– 2+6 =4 Aljabar Linear 13

Sehingga matriks kofaktor dari A : Maka matriks Adjoin dari A adalah : Aljabar Linear 14

• Invers Matriks dengan menggunakan Adjoin • Maka, tentukan invers dari matiks A sebelumnya!

Latihan Bab 2 1. Tentukan determinan matriks dengan determinan/cramer dan ekspansi kofaktor dan 2. Diketahui : dan Tunjukan bahwa : det (A) det (B) = det (AB) Aljabar Linear 16

3. Diketahui : Tentukan k jika det (D) = 29 4. Diketahui matriks Jika B = A-1 dan At merupakan transpos dari A. Tentukan nilai Aljabar Linear 17

Sifat-sifat determinan 1. 2. 3. 4. 5. 6. 7. det(AB)=det(A)det(B) det(AT)=det(A) Jika A matrik diagonal, maka det(A)=a 11 a 22. . . ann {perkalian dari semua entri pada diagonal utama} Jika A matrik segitiga, maka det(A)=a 11 a 22. . . ann {perkalian dari semua entri pada diagonal utama} Jika Anxn, maka det(k. A)=kndet(A) det(A-1)=1/det(A) Jika A memuat baris nol atau kolom nol, maka det(A)=0 Aljaar Linear 18

Sifat-sifat determinan 8. Terhadap operasi baris elementer, determinan mempunyai sifat, sebagai berikut: a. b. c. 9. Jika A’ diperoleh dari A dengan cara mengalikan satu baris dari A dengan konstanta k 0, maka det(A’)=k det(A) Jika A’ diperoleh dari A dengan cara menukar dua baris, maka det(A’) = - det(A) Jika A’ diperoleh dari A dengan cara menjumlahkan kelipatan satu baris dengan baris yang lain, maka det(A’)=det(A) Jika A memuat dua baris yang saling berkelipatan atau dua kolom yang saling berkelipatan, maka det(A)=0 Aljabar Linear 19
- Slides: 19